基于多点关联性的尾矿坝位移监测序列异常值诊断*
易思成,康喜明,吴 浩,胡少华
(1.武汉理工大学 安全科学与应急管理学院,湖北 武汉 430070;2.国网内蒙古东部电力有限公司,内蒙古 呼和浩特 010020;3.华中师范大学 城市与环境科学学院,湖北 武汉 430079)
0 引言
我国是矿产资源开采大国,每年产出大量矿石的同时,也会产生大量尾矿集中堆存于尾矿库。作为1种人造高势能重大危险源,尾矿坝边坡一旦失稳导致溃坝,不仅会严重威胁人民的生命财产安全,同时也将对生态环境造成重大破坏,产生不良的社会影响[1]。目前,国内外普遍采用基于传感器的坝体变形监测系统对尾矿坝进行实时在线监测,通过识别出现的异常数据流并报警以确保相关应急处置措施的及时开展[2]。然而,由于尾矿库的地理位置通常较为偏僻,环境恶劣,所设置的传感器容易受到天气、电力供应、其他现场条件等诸多因素的影响,导致其在数据采集及传输过程中受到扰动和干扰,使得监测数据中不可避免地出现各种噪声[3],部分噪声会被监测系统认定为异常数据引发报警,触发不必要的应急响应,浪费大量人力物力。因此,在异常数据诊断过程中,提高对噪声数据和真实异常数据的辨别能力是十分必要的。
目前常用的异常数据诊断方法主要包括统计概率法和基于机器学习的异常诊断2大类。统计概率法的基本思想是根据统计概率分析来确定判别准则,从而检测数据中的异常值。比较常用的判别准则包括3σ准则、格拉布斯准则、狄克松准则等[4]。许贝贝等[5]将3σ准则应用于大坝监测数据,成功剔除4个所设的尖顶异常值;鲁铁定等[6]分别使用格拉布斯准则和狄克松准则对水电厂监测数据进行分析,实现监测数据中异常值的精确定位。随着人工智能和机器学习的不断发展,基于各种智能算法的异常诊断模型逐渐运用于各行业的异常检测之中。Chen等[7]利用局部异常因子算法(LOF)对锂离子电池组电压监测数据进行异常诊断,通过计算各点的局部可达距离找出故障点;Salazar等[8]提出1种基于增强回归树的异常诊断方法,通过对比预测值与实测值的残差来确定大坝异常数据,取得较好的效果。然而,这些异常诊断模型虽能实现对异常值的大致诊断,却无法进一步判断所识别异常值是否包含有噪声。
孤立森林(Isolation Forest,IF)算法作为1种无监督的机器学习算法,近年来被广泛运用于各领域的异常诊断之中[9-11]。由于我国尾矿坝在线监测系统的应用时间较晚,目前针对尾矿坝坝体变形监测领域的异常值诊断模型研究较少。因此,考虑将IF算法应用于尾矿坝位移监测数据的异常值诊断。此外,结合尾矿坝在线监测系统的传感器为多测点布设[12],所测数据之间通常存在一定关联性,因此进一步引入关联规则以实现对噪声数据和真实异常数据的区分。
基于此,针对尾矿坝位移监测数据的异常值诊断,本文提出1种将关联规则和改进IF算法相结合的异常数据诊断模型。该模型通过量化不同测点监测序列的关联性,将关联性较高的序列组成强关联组合,结合强关联组合的同步检测结果区分噪声数据与真实异常值,从而实现对尾矿坝真实异常工况的精确判断。
1 序列关联性分析
监测序列中的异常值包括噪声和真实异常值,需对其进行区分。由于噪声通常由单测点传感器自身因素引起,因此噪声类的异常值仅会在该测点的监测数据中体现;而因环境等因素导致的坝体性态的真实变化(如坝体形变)会在具有强相关性的多条监测序列中同步体现。基于此,对于多个测点的数据监测序列,通过计算各序列间的数据关联性,并将具有强关联性的序列组成强关联序列组,后续检测异常值时结合强关联序列组的同步检测结果可实现噪声和真实异常值的区分。
尾矿坝位移监测序列通常为等长度时间序列,以长度均为m的2组序列A,B为例,采用Apriori算法对A,B测点序列间的关联度进行量化分析。由于序列间的关联性体现为同时间段内数据变化趋势的相似性,因此按照数据变化趋势可将各段子序列分为“显著上升”、“基本持平”以及“显著下降”3类,用最小二乘线性拟合的方式得到子序列斜率k,根据斜率表征序列变化趋势,赋予相应的字母进行表示。首先选用宽度为n的时间窗口对A,B序列进行截取,得到m/n个子序列,接着对子序列数据进行高斯平滑处理以判断数据变化的大体趋势,根据变化趋势进行符号化映射,映射规则如表1所示。

表1 符号化映射规则
完成各子序列符号化映射后,将同一时间段对应的子序列组成1个子序列组(ai,bi),共m/n个子序列组组成1个完整事务集。Apriori算法通过对完整事务集进行挖掘计算,根据计算各项集支持度结果找出其中的频繁项集,再根据频繁项集以及置信度进一步筛选出符合要求的关联规则。设已找出S条关联规则(ai⟹bi),单条规则的支持度记Psup,置信度记为Pcof,A,B序列的关联度和置信度Pcr(A⟹B),Pcf(A⟹B)分别根据式(1)和式(2)进行判断:
(1)
(2)
参考文献[13]对于序列间关联度和置信度阈值选取情况,本文阈值均选取0.5。根据计算得到关联度和置信度均大于0.5的2组数据序列认定为强关联序列。
2 尾矿坝位移监测序列异常值诊断
2.1 监测序列异常值检测
IF算法是1种无监督的机器学习算法,针对异常值在数据集中呈现“少量”和“稀疏分布”的特性,采用分割的思想来实现对异常值的诊断。其基本方法是对数据集进行不断的分割,直到每个点都被孤立出来为止。异常值通常数量稀少且距离样本中心较远,相较于正常点,会被更快孤立出来。由此,算法可通过比较数据集中各点被孤立时分割的次数判断其异常程度[14],所需分割次数越少,表明该点的异常程度越大。IF算法的基本逻辑如图1所示。
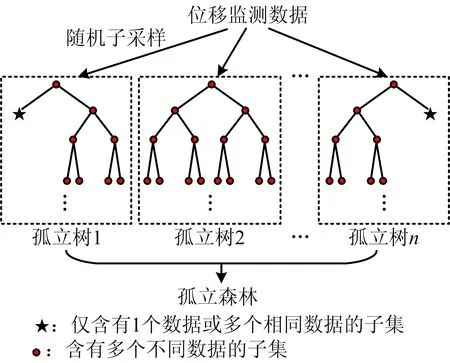
图1 IF算法逻辑示意
算法定义了1个得分公式,以量化数据集中每个点xi的异常程度,得分定义如式(3)所示:
(3)
式中:E(h(x))为x的平均路径长度期望,代表xi的被分割次数;c(n)为标准平均路径长度,代表标准值。
判断标准如式(4)所示:
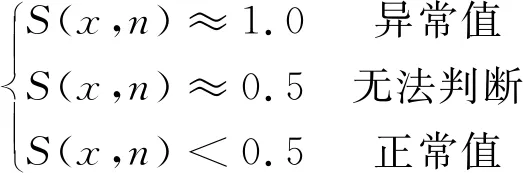
(4)
2.2 云模型优化
由式(3)可知,IF算法实现了对每个数据点异常程度的量化,然而仍存在一定缺陷,即式(4)中对于异常值的分类不够明确。对于[0.5,1]的数据得分区间,得分越接近1,代表异常程度越大,但却并没有明确地给出异常点所对应的准确数值范围,从而导致对于该区间内点是否为异常点的判定结果通常存在一定的主观性。因此,需要1种方法来确定“异常”这一概念与得分区间之间的相互映射关系。
云模型(CM)是1种处理不确定性的计算方法。其中,正向云转换和逆向云转换能够实现知识与数据之间的不确定性认知转换[15],将CM与IF相结合(IF-CM)能够确定IF算法得分与异常概念的映射关系。标准云模型如图2所示。

图2 标准云模型
Ex,En,He分别代表期望、熵、超熵3个数字特征值,μ(x)为隶属度,此处可代表“正常”概念的确定程度。其中Ex在数值上等于序列样本的均值,反映序列中大部分数据的集中分布,根据异常点所具有的稀疏分布特性[16],可认为得分处于Ex附近的点代表正常点,反映“正常”的定性概念。En是定性概念随机性的度量,可反映在论域空间可被概念接受的云滴的取值范围,根据文献[17]计算结果,位于(Ex-3En,Ex-2En)和(Ex+2En,Ex+3En)中的云滴对“正常”概念的贡献度仅有4.3%,而落在此区间外的云滴对表征的定性概念几乎无贡献。由此,若将IF计算的得分作为衡量各点正常程度的变量,可认为得分Ex+2En为正常概念的边界阈值,(Ex+2En,1)区间为异常区间,落于该区间的点为异常点,从而实现异常概念与得分之间的映射。
2.3 结合关联性的异常数据诊断模型
对于经云模型改进后的IF算法所检测出的异常点,需进一步区分噪声与真实异常值。结合序列关联性分析,具体操作步骤如下:根据Apriori算法计算各待测序列的关联度,将具有强关联性的序列进行组合。使用IF算法对各序列进行异常值初筛,引入CM算法优化异常值的判定结果;对于关联性不强的序列,检测结果直接认定为真实异常值;对于强关联序列组,根据检测结果进行进一步判定:序列组中同时刻检测出的异常点认定为真实异常值,否则认定为噪声。
结合多点关联性的异常数据诊断流程如图3所示。
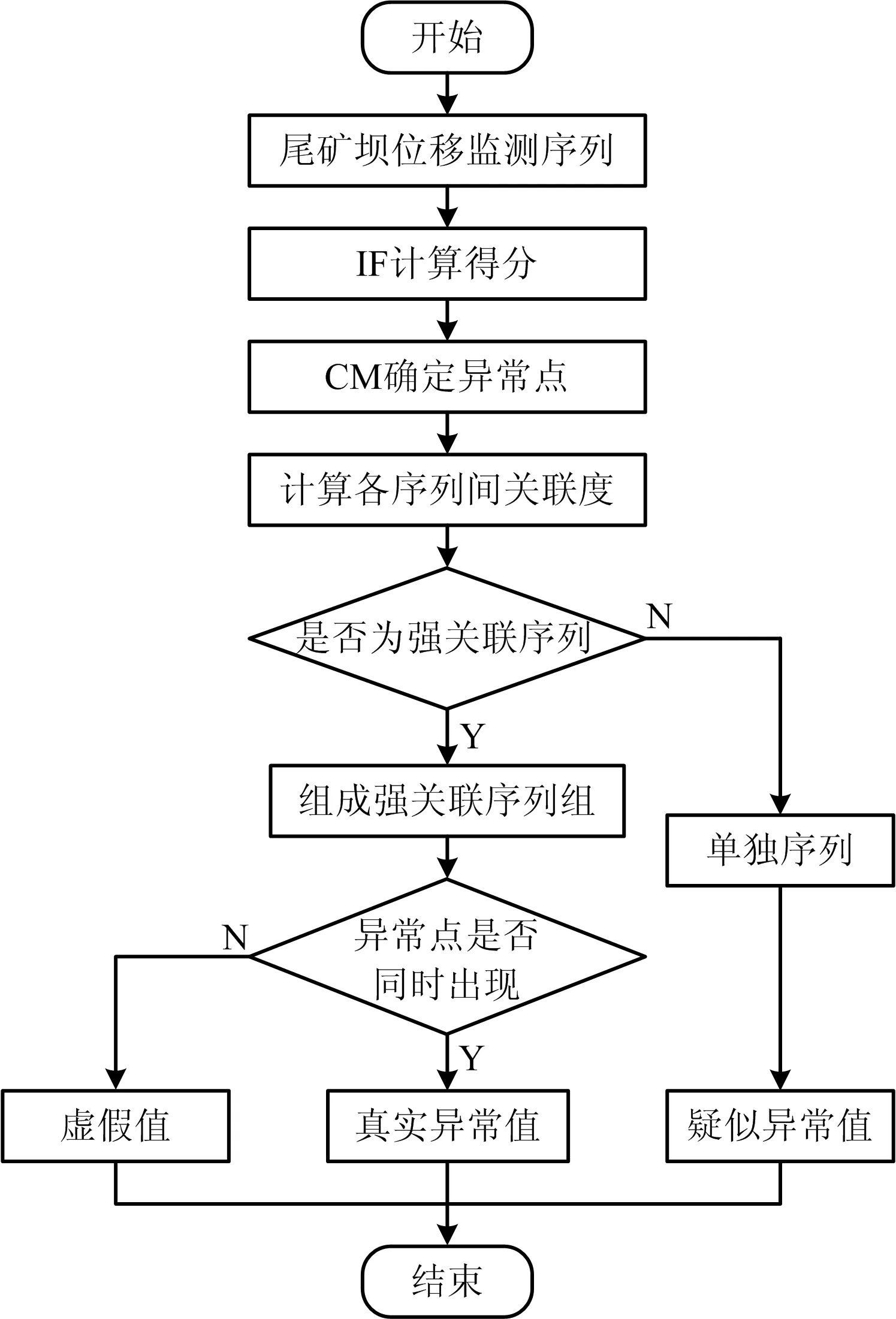
图3 多点关联性的异常数据诊断流程
3 工程应用
3.1 工程概况
湖北省某尾矿库为山谷型尾矿库,坝长146.45 m,坝顶宽5 m,坝顶标高50 m。每级子坝高度为3 m,现已堆积至15期子坝,堆积标高为95 m,总库容达1 469.34 m3。该尾矿库于2014年完成在线监测系统的投入运行,通过GPS技术对坝体表面位移进行在线监测,共布设12个监测点,平面布置如图4所示。本文选取GB1,GB2,GB3测点于2019年第一季度的地表位移监测数据作为样本序列进行模型验证。
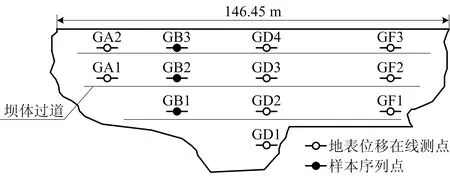
图4 坝体测点平面分布
3.2 关联性分析
由于测点数量较多,因此仅以GB2,GB3所测序列为例进行关联度分析,如图5所示。GB2,GB3原始序列如图5(a)所示,序列长度均为400,滑动窗口宽度n设定为20,因此可截得子序列个数m/n=20,对20个子序列进行高斯平滑处理,处理后图像如图5(b)所示。

图5 GB2,GB3监测序列
GB2,GB3同时段子序列构成子序列组,所有子序列组构成完整事务集。使用Apriori算法找出频繁项集并确定关联规则,结果如表2所示。

表2 GB2,GB3序列关联规则计算结果
由式(1)~(2)可计算得到GB2,GB3序列的关联度和置信度均为0.84,大于所设定的阈值0.5,因此认为GB2,GB3序列为强关联序列。
分别对该尾矿坝12个测点关联性计算,结果如表3所示。

表3 某尾矿坝各测点序列关联性计算结果
以GA2测点为基准点,位于同高程水平线方向上GB3,GD4,GF3测点的关联度分别为0.81,0.62,0.54,置信度分别为0.73,0.56,0.49,根据前文判断,GA2可分别与GB3,GD4组成强关联序列。从关联度和置信度的变化趋势可以看到,随着测点间距离的增加,关联性逐渐下降,当测点间距达到一定阈值时,可认为2测点间不再具有关联性。这说明虽然尾矿坝同高程水平线上各地表点位移变化存在连带效应,但其效应量有限,当坝体同高程2点距离超过一定范围时,则这2点位移变化相对独立,在对其异常值进行分析诊断时,应视为2条独立序列,不能将其进行组合。
以GD4为基准点,位于同一垂线方向上GD3,GD2,GD1测点的关联度分别为0.85,0.69,0.55,置信度分别为0.85,0.62,0.50,关联度、置信度同样随着测点距离的增加而下降。此外,通过对不同高程相邻测点关联度的对比分析发现,处于坝体上游位置的相邻测点序列关联度更高。例如:GD4与GD3关联度为0.85,大于GD2与GD1的关联度0.63。这是由于尾矿坝处于不断的增高加载过程所致,随着时间的推移,坝体逐渐增高,沉降中心上移,下游坝体的尾砂在自身重力以及外部荷载的影响下逐渐变得密实,其位移变化幅值小,导致测点序列关联性不明显。
3.3 模型诊断
根据上文分析计算,该尾矿坝各监测点两两之间共可组成34组强关联序列组,由于数量较多,本节选用GB1,GB2,GB3测点的数据序列作为样本进行模型验证。在3组序列中分别设置一定数量的噪声和真实异常值用于模拟尾矿坝传感器监测过程中的异常工况,分别使用IF算法和IF-CM结合算法对3条序列进行异常值诊断,诊断结果如图6所示。其中,GB1序列诊断结果如图6(a)和图6(b)所示,GB2序列诊断结果如图6(c)和图6(d)所示,GB3序列诊断结果如图6(e)和图6(f)所示。
以图6(c)和图6(d)为例,对于同测点序列诊断,IF算法和IF-CM结合算法对于序列中较为明显的异常值都具有良好的识别效果。然而,对于波动幅度不大的部分数据,IF算法无法进行识别,而IF-CM算法则对其体现出一定的识别能力,因此,当坝体出现异常状况时,使用IF-CM算法能够更快地发现异常数据并报警,从而作出更为及时地响应。
由表3可知,GB1,GB2,GB3测点序列两两之间关联度分别为0.72,0.69,0.84,故这3点可组成强关联序列组。由图6(b)、图6(d)、图6(f)可知,从关联性角度看,在IF-CM算法下,3条序列异常值均得到有效诊断。通过对比发现,3条序列均在285~294处诊断出异常,因此可认为该段序列为真实异常值,监测系统需对其进行报警;GB3序列在第145处诊断出异常点,而GB1,GB2相应位置未见异常,故认为该位置异常诊断结果为噪声,是由于GB3测点传感器自身状况等因素引起,不属于坝体安全性事故造成,监测系统不予报警;GB1序列在第92处和102处未见异常,而GB2,GB3序列在对应位置却都诊断为异常点,故可判断该位置数据应为真实异常值,GB1序列未见异常的原因是测点处于坝体下游,变形不明显而导致异常点未能得到识别,因此监测系统仍然报警。

图6 GB1,GB2,GB3测点异常诊断结果
4 结论
1)引入改进IF算法的异常值诊断模型对尾矿坝位移监测数据进行处理,构建IF所求的定量得分与“异常”定性概念的相互映射关系,为异常值的判定提供明确的依据。
2)引入关联规则实现对所识别的异常值中噪声和真实异常值的区分,避免监测系统出现对于噪声误报警的现象,提高监测系统报警的准确性。
3)以某尾矿坝位移监测数据作为样本序列进行模型验证,研究结果表明:基于多点关联性的异常诊断模型具有良好的异常值诊断效果。

