基于云物元的老旧社区内涝灾害脆弱性评价*
李昌顺,周科平,林 允
(中南大学 资源与安全工程学院,湖南 长沙 410083)
0 引言
社区是城市的重要组成部分,承载居民生产生活等重要功能。随着我国城市化进程不断推进,部分社区建设时间久远,呈现出基础设施老化、配套服务缺失等问题,对居民生活安全产生直接威胁[1]。全国各地极端恶劣天气频发,对城市尤其是老旧社区带来严峻考验。其中,以“小雨湿鞋、中雨积水、大雨内涝”为代表的城市老旧社区水系统问题是重点问题之一。2016年2月,我国老旧社区改造工作正式启动,尽管目前已形成一定的可复制经验,但在实际推进过程中也暴露出改造工作系统性不足、个性化不强、可持续性不长、居民满意度不高等问题,这与对老旧社区脆弱性现状认识不够全面、评价不够精准有直接关系。
国内外学者针对内涝灾害脆弱性评价展开一定研究。1)基于历史灾情的评价方法,该方法基于对历史灾情数据的归纳分析,准确识别致灾因子,确定历史人员或财产损失率,进而估算不同程度灾害下的损失情况;王豫燕等[2]、张馨仁等[3]通过分析历史暴雨洪涝灾情数据构建脆弱性曲线,展开脆弱性评价。2)基于指标体系的评价方法,其核心是建立脆弱性评价指标体系,根据不同原则选取合适指标进行赋权和数据处理,划分脆弱性等级构建评价模型,并计算评价指标对脆弱性等级的隶属度,常见评价模型包括逼近理想排序法(Technique for Order Preference by Similarity to an Ideal Solution,TOPSIS)、Z-numbers模糊数评价体系、压力-状态-响应(Pressure-State-Response,PSR)模型、层次分析法(Analytic Hierarchy Process,AHP)、熵权法、对抗交叉评价方法等[4-10]。3)基于情景模拟的评价方法,该方法一般借助地理信息系统(Geographic Information System,GIS)、暴雨洪水管理模型(Storm Water Management Model,SWMM)、流域水文模型、MIKE软件等三维地质或水文水动力学模型对内涝情景进行可视化模拟,评价不同灾害情景下的脆弱性程度[11-13]。上述研究主要从城市全局视角展开,难以细化到社区尺度,无法对社区内涝灾害脆弱性进行准确识别和评价。同时,内涝灾害致灾因子自身模糊性与不确定性、内涝灾害防治与老旧社区改造之间的矛盾冲突问题也没有得到有效解决。
因此,本文拟结合老旧社区内涝灾害脆弱性特征,通过AHP-熵权法建立老旧社区内涝灾害脆弱性评价指标体系,运用可拓物元分析理论对老旧社区内涝灾害脆弱性进行评价,并借助云模型对可拓物元评价进行改进,以期建立基于云物元的老旧社区内涝灾害脆弱性评价模型。研究结果可为老旧社区适灾化和海绵化改造提供依据。
1 老旧社区内涝灾害脆弱性评价指标体系
1.1 评价指标体系确定
自然灾害脆弱性与致灾因子危险性、孕灾环境敏感性和承灾体易损性密切相关。因此,通过结合自然灾害相关理论,并遵循科学性、系统性、独立性和易获取性原则,在文献研究和实地调研基础上邀请8名相关领域专家,采用德尔菲法识别并确定老旧社区内涝灾害脆弱性评价相关指标,建立老旧社区内涝灾害脆弱性评价指标体系。同时,参照《中华人民共和国防汛条例》(2011年1月8日修正版)、《防汛抢险技术手册》以及各地防汛应急预案,分析中国地面气象站数据集和2016—2020年国家与地方统计年鉴。依据标准规范得到各指标在不同脆弱性等级下的参考范围,见表1。

表1 老旧社区内涝灾害脆弱性评价指标体系
1.2 评价指标权重确定
在老旧社区内涝灾害脆弱性评价中,评价指标权重会对评价结果造成显著影响,因此,本文运用层次分析法获取主观权重,运用熵权法获取客观权重,通过加法合成法获得各指标的组合权重。
1)主观权重确定
结合表1及专家打分,按照1~9标度法对各指标进行两两比较构造判断矩阵,并进行归一化处理,如式(1)~(2)所示:
(1)
(2)
式中:Mi为判断矩阵每行元素的乘积;aij为所属判断矩阵中第i行第j列元素;Wi为Mi的n次方根;n为判断矩阵阶数;Wi为判断矩阵的特征向量。
权重向量如式(3)所示:
(3)
计算判断矩阵A的特征向量和最大特征根如式(4)~(5)所示:
(4)
(5)
式中:λ为判断矩阵的特征根;λmax为判断矩阵的最大特征根;(AW)i为向量AW的第i个元素。
对判断矩阵进行一致性检验,如式(6)~(7)所示:
CR=CI/RI
(6)
(7)
式中:CR为判断矩阵随机一致性比率;CI为判断矩阵一般一致性指标;RI为判断矩阵平均随机一致性指标。
当CR<0.1,判断矩阵满足一致性检验,各评价指标权重合理,可得到各评价指标的主观权重。
2)客观权重确定
首先,根据专家打分结果构造判断矩阵,对判断矩阵进行归一化处理并计算信息熵,如式(8)~(10)所示:
(8)
(9)
(10)
式中:Yij和pij为专家打分结果判断矩阵的归一化过程值;Hi为信息熵。
计算指标层和准则层的客观权重,如式(11)~(12)所示:
(11)
(12)
式中:ωi为指标层客观权重;Wk为准则层客观权重;n为指标数;N为准则数。
3)组合权重确定
老旧社区内涝灾害脆弱性评价体系的主观权重ω1和客观权重ω2均已求出,为了使权重更具可靠性,采用加法合成法计算组合权重,如式(13)所示:
W=0.5ω1+0.5ω2
(13)
2 老旧社区内涝灾害脆弱性评价模型建立
2.1 云模型改进的可拓物元评价概述
可拓物元评价理论主要用于处理问题的矛盾性,但在分析和评价过程中不可避免地存在量化值的模糊性和随机性问题[14]。云模型通过将随机确定度赋予样本点,从而得以将定性概念和定量表达集成在一起,统一刻画概念中的随机性、模糊性和关联性[15]。云模型改进的可拓物元评价将有效解决传统物元模型在随机性和模糊性等方面的不足,使评价结论更具可信度。云物元模型如式(14)所示:
(14)
式中:R表示物元;Ex表示期望;En表示熵;He为超熵。
在云物元模型中,以评价指标的不同等级分值作为参照,通过固定区间[cmin,cmax]代表脆弱性等级,根据云模型的“3En”规则将区间数值转换为云参数,如式(15)~(17)所示:
(15)
(16)
He=s
(17)
式中:s为常数。
超熵He大小决定云图厚度。根据信息熵的基本特征,熵值越大,定性概念的模糊性越大。由于在老旧社区内涝灾害脆弱性评估中无需对边界进行严格划分,因此云模型要足够模糊,此时熵值En采用式(18)进行计算:
(18)
由式(15)~(18)计算云参数(Ex,En,He),建立以En为期望、He为标准差的正态分布,确定随机数En′,其中,x为指标值。按照式(19)~(20)计算其对不同脆弱性等级云的隶属度:
(19)
En′=r×He+En
(20)
式中:r为随机数。
2.2 老旧社区内涝灾害脆弱性云物元评价模型
综合文献研究[16-17]并征求专家意见,将老旧社区内涝灾害脆弱性评价指标体系中的各指标划分为Ⅰ、Ⅱ、Ⅲ、Ⅳ、Ⅴ 5个等级,各等级对应分值见表2,并据此对指标数据进行标准化。

表2 老旧社区内涝灾害脆弱性等级与指标分值
根据式(15)和式(18)分别计算Ex和En,并通过MATLAB软件绘制不同He下的老旧社区内涝灾害脆弱性等级隶属云云图,如图1所示。
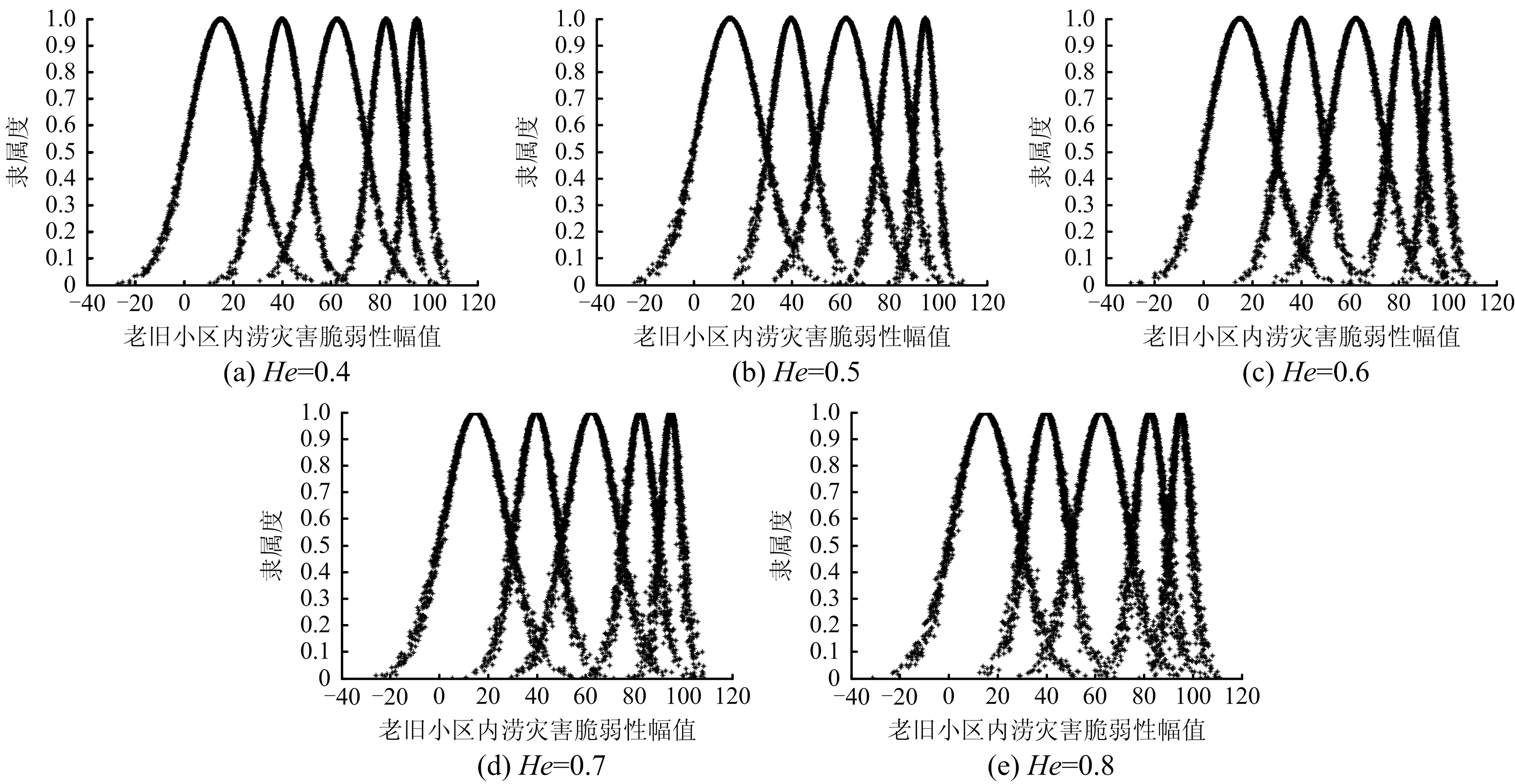
图1 老旧社区内涝灾害脆弱性等级隶属云云图
由图1可知,当He=0.6时,云模型中隶属度大于0.5的部分比较清晰,小于0.5的部分模糊和交叉,模糊性适中,相对于其他He值得到的隶属度更加精确。因此,本文选取He=0.6用于老旧社区内涝灾害脆弱性评估,得到老旧社区内涝灾害脆弱性评价指标体系中不同等级的云物元模型。标准云物元数字特征见表3。

表3 标准云物元数字特征
基于表3可计算脆弱性评价指标体系中各评价指标对不同脆弱性等级的隶属度,考虑其中引入随机数r,计算结果存在较大随机性,因此,重复计算1 500次后取中位数作为各评价指标对不同脆弱性等级的隶属度。
准则层内各准则对不同脆弱性等级的隶属度通过将该准则下各指标对不同脆弱性等级的隶属度加权得到,如式(21)所示:
(21)
式中:μj(Bi)是第i个准则层物元对不同脆弱性等级j的隶属度;Wis是第s个指标对于第i个准则层的组合权重;μj(Iis)是第s个指标层物元对不同脆弱性等级j的隶属度。
计算目标层对不同脆弱性等级的隶属度同上。根据最大隶属度原则,不同物元所属的脆弱性等级L如式(22)所示:
(22)
3 案例分析
3.1 长沙市某社区内涝灾害脆弱性评价
本文以长沙市科学村社区为例,对上述评价模型进行验证和分析。该社区截止2021年已建成并投入使用达29 a,属于典型的老旧社区,随周边配套设施建设,该社区得以提质提档改造,社区绿地、雨污管网、外部空间得到极大优化。经实地测算,该社区占地面积约85 000 m2,其中绿化面积约10 000 m2,相对高程差约5 m,居住人口约3 000人。
以J=(Ⅰ,Ⅱ,Ⅲ,Ⅳ,Ⅴ)作为科学村社区内涝灾害脆弱性评价等级,分别对应脆弱性低、较低、中等、较高、高。在实地调研及专家访谈基础上,综合运用德尔菲法识别建立老旧社区内涝灾害脆弱性评价指标体系和各指标权重,并结合专家打分结果运用AHP-熵权法确定评价指标权重和各指标分值,见表4。
基于本文模型及表4打分结果,按照式(21)~(22)计算各指标脆弱性等级隶属度,以每个指标为1个云滴,云滴隶属度是服从正态分布的随机数,随机试验1 500次后取中位数作为该云滴对科学村社区内涝灾害脆弱性评价等级的隶属度,见表5。

表4 科学村社区内涝灾害脆弱性评价指标权重
3.2 评价结果及分析
由表4可知,无论主观权重或客观权重,承灾体的易损性对于老旧社区内涝灾害脆弱性影响相对最大,组合权重为0.598 4,这与建成时间长、基础设施落后等条件直接关联。孕灾环境的敏感性和致灾因子的危险性同样对老旧社区内涝灾害的脆弱性有直接影响,孕灾环境的敏感性影响略大,这与社区建造和城市发展进程之间的不平衡有关。
由表5可知,科学村社区内涝灾害脆弱性对于各评价等级的隶属度分别为0.349 3,0.670 1,0.086 5,0.000 0,0.000 0,根据最大隶属度原则,科学村社区的内涝灾害脆弱性等级为Ⅱ级,即脆弱性较低。根据准则层隶属度,科学村社区的致灾因子危险性、孕灾环境敏感性和承灾体易损性脆弱性都比较低。细化研究各指标可以发现,科学村社区在绿化面积、不透水面积和排水管网年限等方面控制较好,这与之前进行的老旧社区改造密切相关,同时印证前期老旧社区的改造方向、举措是有效的。因此,在下一步工作中可继续通过加强对外部空间的优化设计,尤其在是绿地的改扩建、排水管网的更新等方面降低老旧社区内涝灾害脆弱性,也可以通过进一步优化社区网格化服务、加大内涝灾害防御宣传教育等方式进一步提高老旧社区居民主动抵御内涝灾害的能力。

表5 科学村社区内涝灾害脆弱性评价指标隶属度
4 结论
1)综合运用德尔菲法、AHP-熵权法建立老旧社区内涝灾害脆弱性评价体系,涵盖致灾因子危险性、孕灾环境敏感性和承灾体易损性3个1级指标和年度暴雨及以上天气频率、社区相对高程、人口密度等15个2级指标。
2)基于可拓物元评价理论和云模型,构建老旧社区内涝灾害脆弱性评价云物元模型,该模型较传统物元分析模型具有更好的随机性和模糊性,可以准确、直观地反映老旧社区内涝灾害脆弱性的影响因素,为老旧社区适灾化和海绵化改造提供切实可行工具。
3)老旧社区内涝灾害脆弱性评价是城市内涝防治的微小缩影,本文只初步探究社区层面内涝灾害脆弱性评价的方法和步骤,指标选取、权重计算和脆弱性等级划分等方面有待进行更加深入的研究。

