过载、破损及老化风险场景的单芯PVC电缆温升研究*

陈小龙，黄国忠，高学鸿，欧盛南，李春晖

(1.北京科技大学 土木与资源工程学院，北京 100083；2.北京科技大学 大安全科学研究院，北京 100083；3.华为技术有限公司，广东 深圳 518129)

0 引言

PVC电缆被广泛应用于工厂、建筑、学校等场所的电力运输中。随城市人口增长和电缆运行环境日益复杂，电缆破损和老化逐渐加重，加之部分电缆长期处于过载场景下，火灾事故时有发生。据统计，2015—2020年我国共发生已查明原因电气火灾58.7万起，超过火灾发生总数1/3，其中由于电线电缆原因引发的火灾占据较大比例。电缆内因火灾不是突发的，而是1个电缆温度升高，最终导致绝缘材料燃烧发生火灾事故的过程[1]。因此，研究过载、破损、老化等多风险因素耦合场景下的电缆温升，对电力电缆内因火灾预警具有指导意义。

国内外学者对电缆火灾点燃原理、过载温升计算理论、过载温升试验等方向进行研究。关于电缆火灾点燃机理：Babrauskas[2]、吕亮等[3]、Courty等[4]、Fisher等[5]提出电缆火灾主要点燃机制包括电弧故障、电缆芯过热和外部加热；Zhang等[6]研究绝缘材料老化对PVC电缆火灾点燃的影响；Babrauskas[7]总结制造缺陷、过载、局部破损、力和蠕变等因素对PVC电缆点火的影响。关于通电电缆温升计算方法：汪凯[8]推导出电缆温升随时间变化的双指数型曲线理论模型；郝海滨[9]和刘刚等[10]考虑基于热路模型的电缆轴向传热过程并建立单芯电缆的三维热网络模型；胡倩楠[11]建立三芯电缆导体温度计算的热路模型；Holyk等[12]研究多芯电缆稳态温度的模拟与测量。此外，研究人员针对过载危害开展研究，分析不同过电流条件下高温线芯对线缆绝缘材料和周围其他可燃物的引燃特性[13]；高俊国等[14]通过火灾动力学仿真对比分析新旧标准电缆的燃烧情况。目前，对于PVC电缆温升的研究主要集中在理论模型和电缆温升火灾危险性分析方面，部分学者仅针对单因素风险场景下的电缆温升进行一定研究，忽略多因素耦合场景下的电缆温升规律。

鉴于此，本文基于传热学理论和电缆耦合试验开展定性与定量综合分析，对过载、破损及老化等多因素耦合风险场景下的单芯PVC电缆温升进行深入研究。

1 单芯电缆温升方程及热平衡函数

接入恒流回路的电缆，内芯导体在电流热效应作用下产生热量并传递给绝缘层，绝缘层同时向外界环境散发热量。设电缆内芯的温度为TC，环境温度为T0，其产热和散热的物理过程遵循能量守恒定律，电缆温升为产热与散热之差，如式(1)所示：

(1)

式中：t为通电时间，s；m为电缆内芯线密度，kg/m；C为电缆比热容，J/(kg·℃)；R为单位长度的内芯电阻，Ω/m；T为电缆温度，℃；T0为外界环境温度，℃；Kzh为电缆绝缘层与外界总换热系数，J/(m2·℃)；A为单位长度电缆比表面积，m。

对式(1)求一阶微分方程得到温升ΔT，如式(2)所示：

(2)

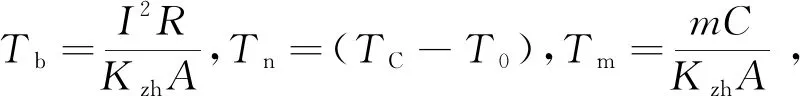
(3)

式中：Tb，Tn，Tm为3个可调系数，分别表示平衡温升系数、温差系数和时间系数。Tb由电流大小、电缆散热状态及自身材料特性共同决定；Tn由线芯内外温差所决定，可能受电流及材料的综合作用影响；Tm与电缆散热及绝缘材料有关。

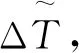
(4)

(5)

其中电缆表面总换热系数Kzh受电缆表面和环境热传导、热对流和热辐射状况的影响。因此，试验研究将进一步探究电流(过载)以及影响电缆表面换热系数的各种风险因素(老化、破损)对单芯PVC电缆平衡温升的影响规律。

2 电缆温升试验

2.1 试验设备和材料

试验采用长0.75 m、截面积0.75 mm2的内部布线单芯软导体无护套电缆(60227IEC 05 BV)，电缆参数如图1所示。试验中TSO6210型接地电阻测试仪与待测电缆形成回路，提供稳定恒流；电缆温度通过T型热电偶进行测量；LR8431-30型数据采集仪记录电流、温度等参数；老化试验箱可提供恒定温度的老化环境用于制作老化电缆样品。

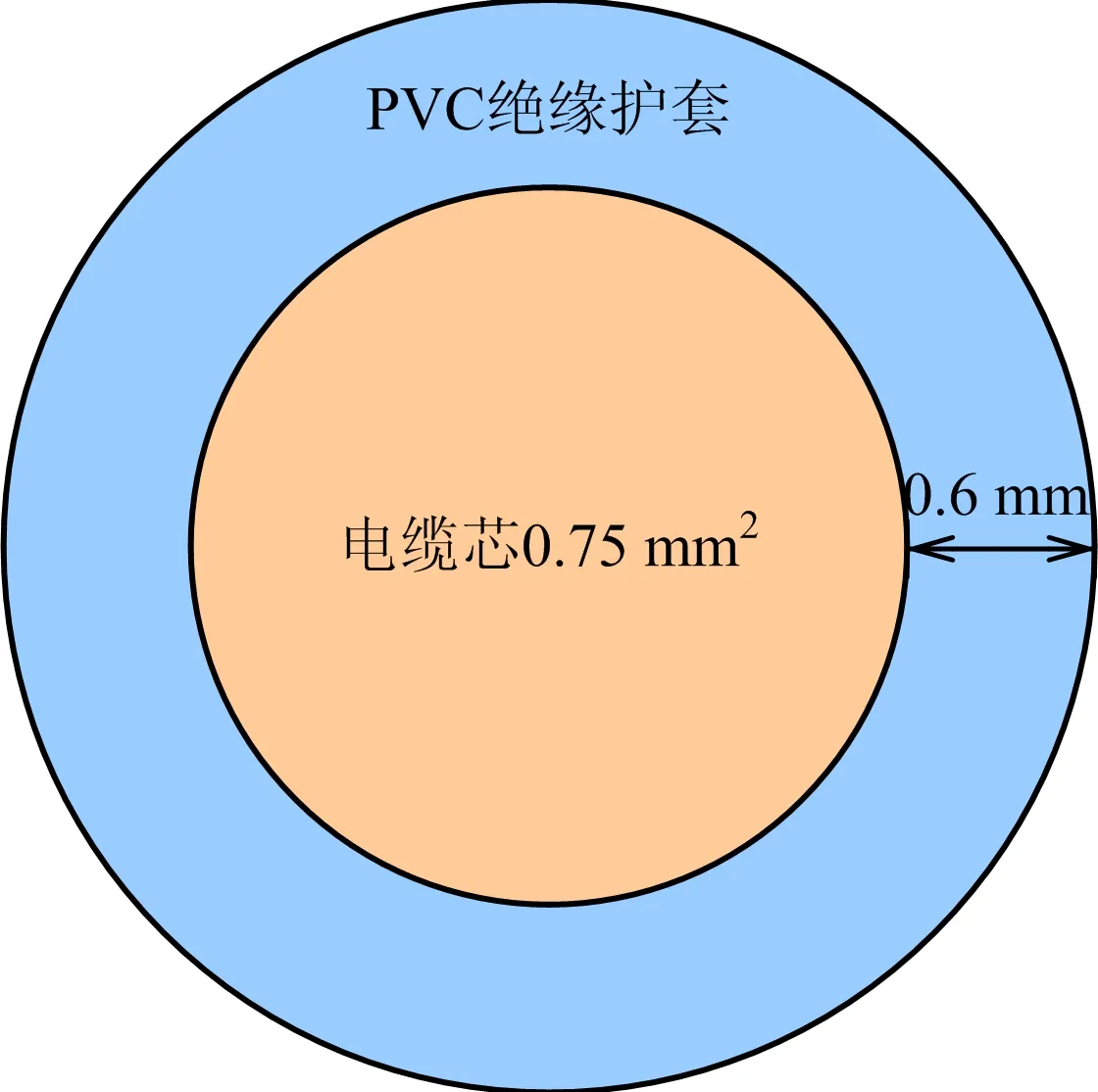
图1 电缆截面示意

2.2 试验设计

针对电缆温升风险影响因素，试验选取6种不同大小电流，3种绝缘层机械破损程度和4种老化状态场景进行组合测试，记录电缆两端、中端以及破损边缘处的温度变化。

1)过载单因素变化试验组

电流是影响电缆温升的主要因素，本组试验探究电缆在不同电流下温升随时间的变化规律，同时研究不同过载电流下电缆平衡温升与电流之间的关系。根据实际电缆载流量计算2.5 mm2以下线径电缆的安全允许载流量为电缆线径的9倍，试验电缆长期工作的安全载流量应小于6.75 A，同时该电缆正常工作的最高承受温度为70 ℃。基于此，设计6，10，13，15，18，20 A 6种不同大小的电流，对电缆通电850～999 s，并对22，25 A的严重过载情况进行短时间测试。

2)过载-机械破损试验组

电缆在布线或工作过程中由于机械损伤或动物啃咬等原因导致电缆绝缘层局部破损，改变其散热条件，破损边缘的绝缘层吸收到更多热量，加剧电缆绝缘层的破坏甚至起火。试验采用在10 mm长度电缆中绝缘层的损失比例表征电缆不同局部受损程度，如图2所示，测量电缆破损边缘处在不同破损率和电流下的温度变化，探究不同破损程度对电缆温升和平衡温升的影响。

图2 电缆绝缘层局部破损程度示意

3)过载-老化试验组

服役时间过长的电缆受老化影响，绝缘层变硬、开裂、内部结构改变，导致绝缘层绝缘能力和抵御高温的能力逐渐减弱[15]，电缆更易发热，火灾风险大大增加。通过采用不同老化程度的电缆在不同过载条件下进行试验，探究老化对电缆温升的影响。利用老化试验箱对电缆进行加速寿命处理，处理时间由Arrhenius加速老化模型进行推理。Arrhenius认为对于同一反应，物质的活化能保持不变，不同温度下部件寿命与温度指数倒数成反比[16]，如式(6)所示：

(6)

式中：V表示反应速率，mol/(m3·s)；A表示比例常数；Ea为激活能，0.3～1.2 ev(聚氯乙烯为1.01 ev)；T为开氏温度，K；K为玻尔兹曼常数，K=8.617 385×10-5。

仅考虑热因素，电缆的热老化程度与时间和温度关系可通过阿伦纽斯模型进行分析。参考《额定电压450/750V及以下聚氯乙烯绝缘电缆 第2部分：试验方法》(GB/T 5023.2—2008)[17]中对60227IEC 06(BV)的老化测试环境建议，选择老化温度为80 ℃，老化因子为642.7,根据Arrhenius加速老化模型得到加速老化处理时长见表1。

表1 加速老化处理时长

4)过载-破损-老化耦合试验组

该组试验对6种不同大小电流，3种不同绝缘层机械破损程度和4种不同老化时间的电缆进行交叉耦合试验，以得到电缆在不同过载、破损及老化综合风险耦合作用下的电缆温升规律。

3 电缆温升分析

首先对试验电缆进行过载单因素试验，得到不同通电电流下电缆温升随时间变化曲线如图3所示，图中温升曲线由下到上分别表示6，10，13，15，18，20，22 A通电电缆的温升变化，各电缆温升变化趋势一致。通电初期，电缆温升速率较快，一段时间后温升速率逐渐变慢，最终达到某一温度值并维持在该温度上下波动，符合式(3)的电缆温升方程。当电流在电缆允许范围内或轻微过载时，电缆平衡温升差异较小，当电缆发生过载时，温升较为显著，电缆火灾风险增大。

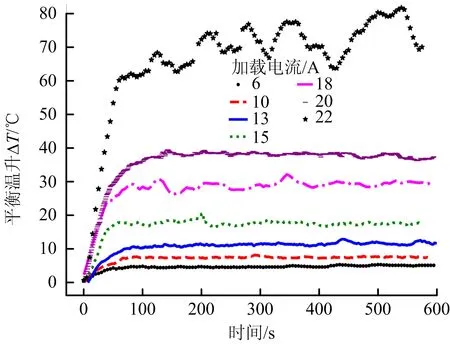
图3 不同加载电流下电缆平均温升曲线

为研究过载电缆温升随时间变化规律，通过试验数据拟合温升方程来量化电流对电缆温升的影响。为方便函数拟合，将电缆温升方程简化为式(7)：

ΔT(t)=a(1-ebt)+cebt

(7)

式中：ΔT表示电缆温升，℃；t表示时间，s；a,b,c均表示拟合参数。

剔除离群点后拟合情况如图4所示，稳健模型主要剔除900～1 000 s温度出现大幅度下降的部分，该变化明显不符合电缆温升规律，稳健拟合后的均方根误差下降到4.05，拟合效果有所提升。拟合后22 A电流下的温升曲线表达式如式(8)所示：

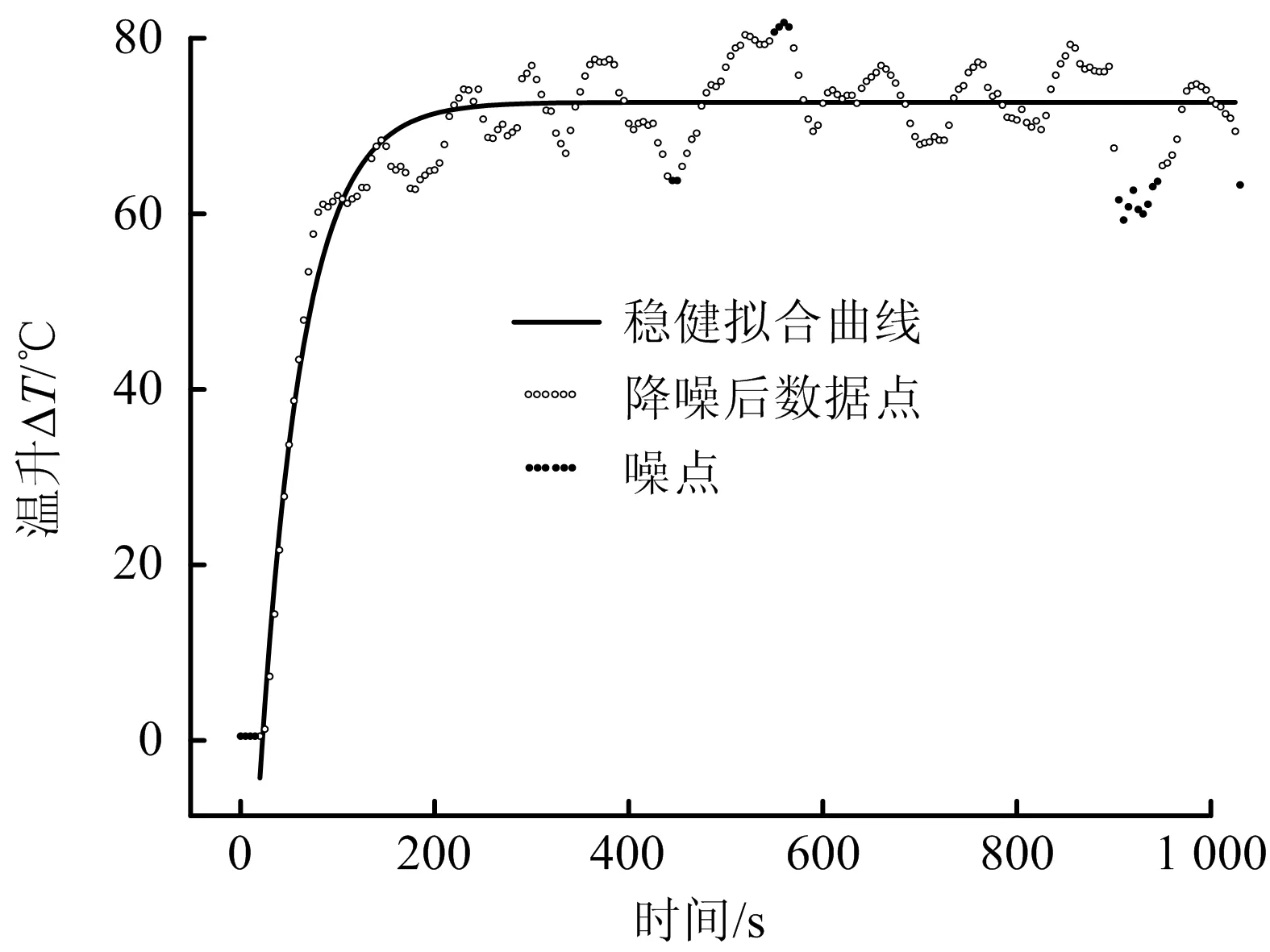
图4 剔除离群点后拟合情况(22 A)

ΔT(t)=72.71(1-e-0.022 7t)-48.52e-0.022 8t

(8)

试验中不同破损和老化程度的电缆温升变化趋势与正常电缆一致。但当电流相等时，破损率和老化程度越高，电缆平衡温升越大，说明破损和老化不会影响电缆温度的整体上升规律，但会加强电缆过载情形下的火灾危险性；破损率为50%时，正常电缆与破损电缆平衡温升差异较小；破损率为75%时，平衡温升差异较为显著；破损率为100%时，局部裸露的线芯对破损边缘的加热效应更加明显。对比正常电缆，老化会使过载情景下的电缆耐热性能显著恶化，老化作用对电缆温升影响过程为快速恶化-缓慢恶化-迅速恶化，类似于机械失效的浴盆曲线。

4 电缆平衡温升分析

电缆热平衡函数和温升试验均表明通入电流的电缆最终会达到某一平衡温度，平衡温升决定电缆最高温度，对电缆内因火灾风险分析至关重要。因此，分别研究过载、过载-老化、过载-破损、过载-老化-破损等组合风险场景下的电缆温升，量化不同风险场景对电缆温升的影响意义重大。

4.1 正常电缆平衡温升

由电缆热平衡函数式(4)可知，电阻和表面积一定，平衡温升与电流平方成正比，与导线总换热系数成反比。不同通电电流下，电缆平衡温升散点和拟合后的电流-平衡温升曲线如图5所示。

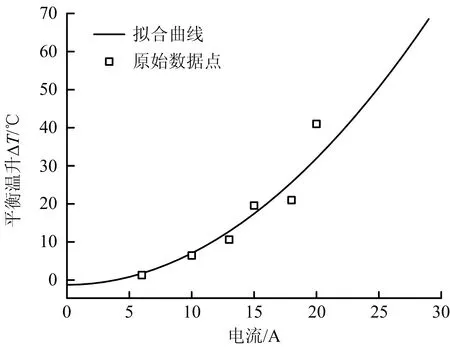
图5 正常电缆平衡温升散点及二次函数拟合曲线

由图5可知，平衡温升与电流符合平衡温升方程。将拟合目标函数式(4)简化为y=ax2+b，其中，自变量x为电流，因变量y为平衡温升，a和b为待拟合的系数。二次项系数a与总换热系数相关，常数项系数b为修正项，非线性拟合的均方根误差RMSE为2.14，置信度高。拟合后正常电缆的平衡温升值与电流关系如式(9)所示：

TB(I)=0.083I2-1.259

(9)

4.2 破损电缆平衡温升

为进一步量化破损程度对电缆平衡温升的影响，首先通过稳健拟合不同电流和破损率下的电缆温升函数得到平衡温升数据点。不同破损程度电缆的平衡温升与电流呈二次函数关系，如图6(a)所示，破损率越高，平衡温升曲线越陡峭，表明破损程度与平衡温升中电流的二次项系数具有较强的相关性。为探索破损率对平衡温升函数系数的影响，对不同破损程度下的平衡温升点进行二次函数拟合，得到图6(b)，其利用热力图对2者线性相关性进行分析，1表示2个变量完全线性相关，0表示2个变量完全线性无关。由图6(b)可知，二次项系数与破损率之间存在极强的线性关系。根据电缆温升函数，二次项系数与总传热系数相关，表明局部破损会破坏电缆的传热状态，导致相同电流下破损电缆的平衡温升高于正常电缆。通过线性回归拟合得到破损率与二次项系数之间的线性函数，如式(10)所示：

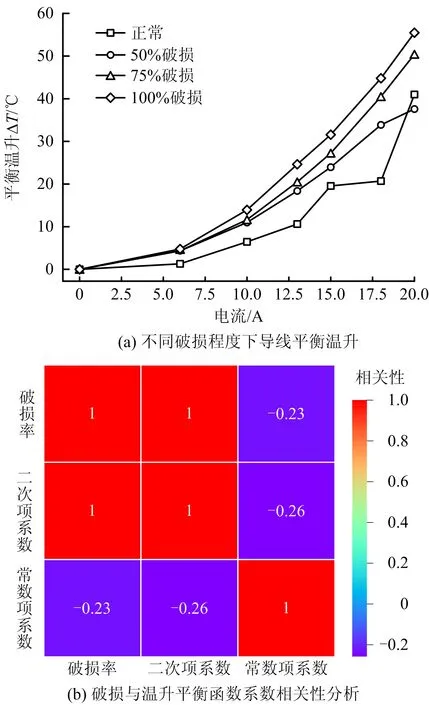
图6 不同破损程度下电缆平衡温升分析

G(s)=0.076 85s+0.064 97

(10)

将式(10)作为平衡温升函数的二次项系数得到破损电缆的平衡温升，如式(11)所示：

TB(I,s)=(0.076 85s+0.064 97)I2-0.283 9

(11)

式中：TB表示平衡温升；I表示电流，A；s表示破损程度，s∈[0,1]。

4.3 老化电缆平衡温升

基于数值分析定量研究老化对电缆平衡温升的影响程度，不同老化时间电缆的平衡温升与电流关系曲线如图7(a)所示，老化电缆平衡温升与电流呈二次函数关系，说明老化本身不会直接导致电缆温升。当电流相同时，老化时间越长，电缆平衡温升越大，且电流-平衡温升曲线越陡峭。由此推测老化时间与平衡温升函数中的电流二次项系数相关，即老化对电缆表面的总换热系数有影响。

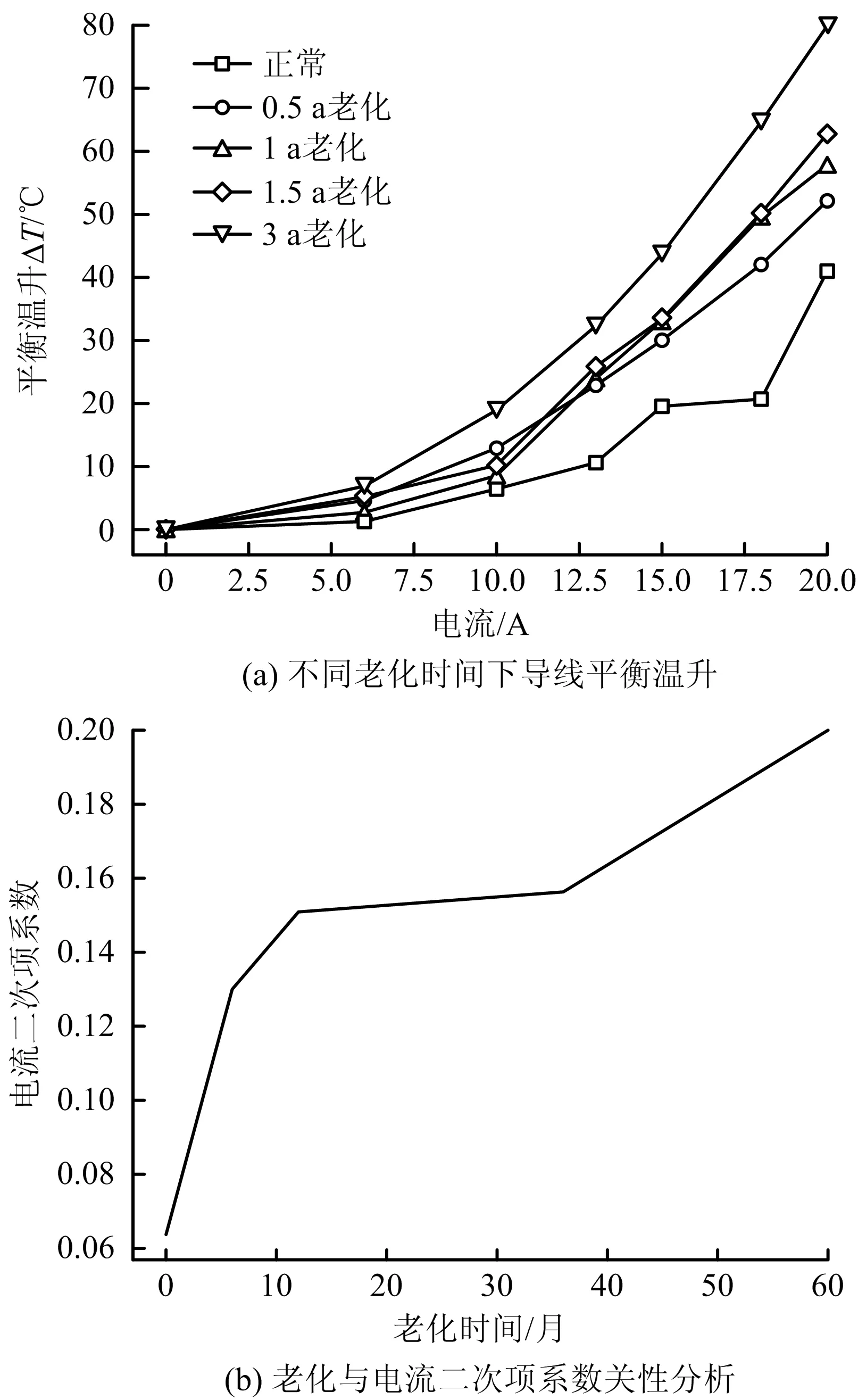
图7 不同老化程度下电缆平衡温升分析

为分析老化时间对平衡温升函数中电流二次方项系数的影响关系，对不同破损程度下的平衡温升点进行二次函数拟合如图7(b)所示，老化时间与电缆温升函数中的电流二次项系数拟合曲线图呈S型。新电缆和接近使用寿命的旧电缆的老化对平衡温升的二次项系数影响较大，而正常使用电缆的老化对电流二次项的系数影响不明显。基于流变突变模型，当新电缆使用一段时间后，电缆绝缘材料高聚物的链式结构破坏，电缆总换热系数发生改变，老化影响平衡温升的现象明显；当电缆老化时间处于寿命周期内，绝缘材料缓慢破坏但电缆不会彻底失效，老化影响平衡温升的现象不明显；当老化时间超过电缆使用寿命，绝缘材料会加速恶化并使其处于报废状态，此时过载后电缆火灾风险大幅升高。

为简化流变突变模型，采用二元高次函数对2者关系曲线进行拟合，多次拟合后发现4次函数拟合的拟合优度R-Square为0.978，效果较好。老化时间对平衡温升函数影响的拟合关系式如式(12)所示：

TB(I,a)=(-1.002×10-7a4+1.522×10-5a3-0.000 766 8a2+0.015 12a+0.063 7)I2-0.283 9

(12)

式中：TB(I,a)表示电流和老化因素作用下的电缆温度，℃；I表示电流，A；a表示电缆老化时间，月。

4.4 过载、破损及老化耦合风险场景温升拟合

在PVC电缆过载试验中，电流是电缆温升的主要致因，是电缆过热的热量来源，破损率和老化程度则通过影响电流致热的二次项系数进一步影响电缆平衡温升。破损率-电流温升函数TB(I,s)和老化-电流温升函数TB(I,a)分别是破损率s和老化时间a的1次和4次函数，基于最小二乘法的参数估计对过电流、破损及过载耦合情形下的电缆温升进行分析。耦合情形下PVC电缆的温升表达式TB(I,s,a)如式(13)所示：

(13)

式中：p1～p7为待估计的参数；I,s,a分别表示电流、破损率和老化时间。

利用Python数据分析工具包对耦合温升表达式进行最小二乘法拟合，拟合参数见表2。

表2 拟合参数数值

5 结论

1)结合电流热效应和传热学建立电缆温升方程和热平衡函数。单因素和多因素耦合风险场景下单芯PVC电缆温升趋势一致；通电初期温升速率较快，一段时间后温升速率逐渐变慢，最终达到某一温度值并维持在此温度上下波动。

2)电缆散热环境未改变情况下，电缆平衡温升与过载电流呈二次函数关系；电缆局部破损程度通过线性关系影响电缆平衡温升二次项系数；电缆老化程度通过流变突变函数关系影响平衡温升二次项系数。

3)在电缆多因素致热过程中，过载是电缆温升的主要原因，破损率和老化程度通过影响电缆材料及传热条件进一步影响电缆平衡温升。