基于改进飞蛾扑火算法的应急资源调度研究*
黄彩霞,刘年平,谢晓君
(西南科技大学 环境与资源学院,四川 绵阳 621000)
0 引言
由于各类突发事件频发,对人民群众的生命财产安全造成巨大威胁,应急资源的及时安排和合理调度对减小灾后损失极其重要,因此,研究应急资源调度模型意义重大。
在研究应急资源调度模型方面:Kemball-Cook等[1]提出针对性管理应急资源的供应和运输;List等[2]在放射性危险物品运输优化模型中引入应急概念,为后续应急资源调度研究奠定基础;王妍妍等[3]提出实时更新应急物资的大数据信息;巩玲君等[4]考虑灾后应急资源调度的优先顺序;盛虎宜等[5]基于灾后物资调度公平性建立多目标优化模型;Wang等[6]建立以最少时间、最低成本为多目标的二维优化模型;Jiang等[7]考虑运输时间、道路通行程度和物资调度需求,建立应急物资车辆调度模型;薛星群等[8]考虑通行约束力和运力限制的灾后应急物资调度;田晓勇等[9]结合道路抢修情况考虑应急调度优化问题。
在求解应急资源调度模型算法方面:孙欣欣等[10]基于遗传算法,以运输时间最少、物资储备库最少建立多目标应急物资调度模型;张永领等[11]提出基于混沌粒子群算法的应急资源调度模型;王付宇等[12]提出基于改进天牛须算法的应急资源调度模型;Mirjalil[13]提出飞蛾扑火优化(MFO)算法求解应急物资调度最优化问题;贺体龙等[14]基于改进飞蛾扑火群智能算法,研究道路损坏情境下多需求点的应急资源调度问题;Trivedi等[15]提出Levy-MFO算法(LMFO)求解应急物资调度方案。上述研究成果极大地推进了应急资源调度水平,但随着灾害事故现场的复杂化、动态化,单一的设计指标不能很好地反映应急资源调度的合理性、及时性。同时,伴随应急资源调度模型优化,求解应急资源调度模型的传统遗传算法、粒子群算法、MFO算法等存在陷入局部最优和全局寻优性能差的问题。
因此,本文在不同运输路况下,构建消耗成本最低、装车时间最少的多目标应急资源调度模型即基于双自适应因子的改进飞蛾扑火算法(DAMFO),用以求解各灾害点的应急资源配置方案,研究结果可为制定合理高效的应急资源调度方案提供依据。
1 问题描述与模型建立
1.1 问题描述
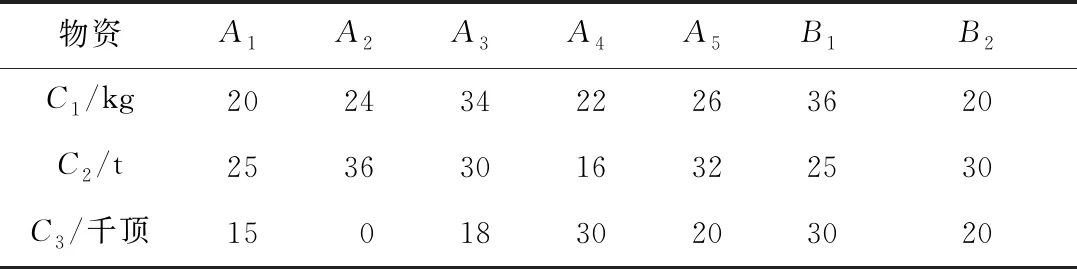
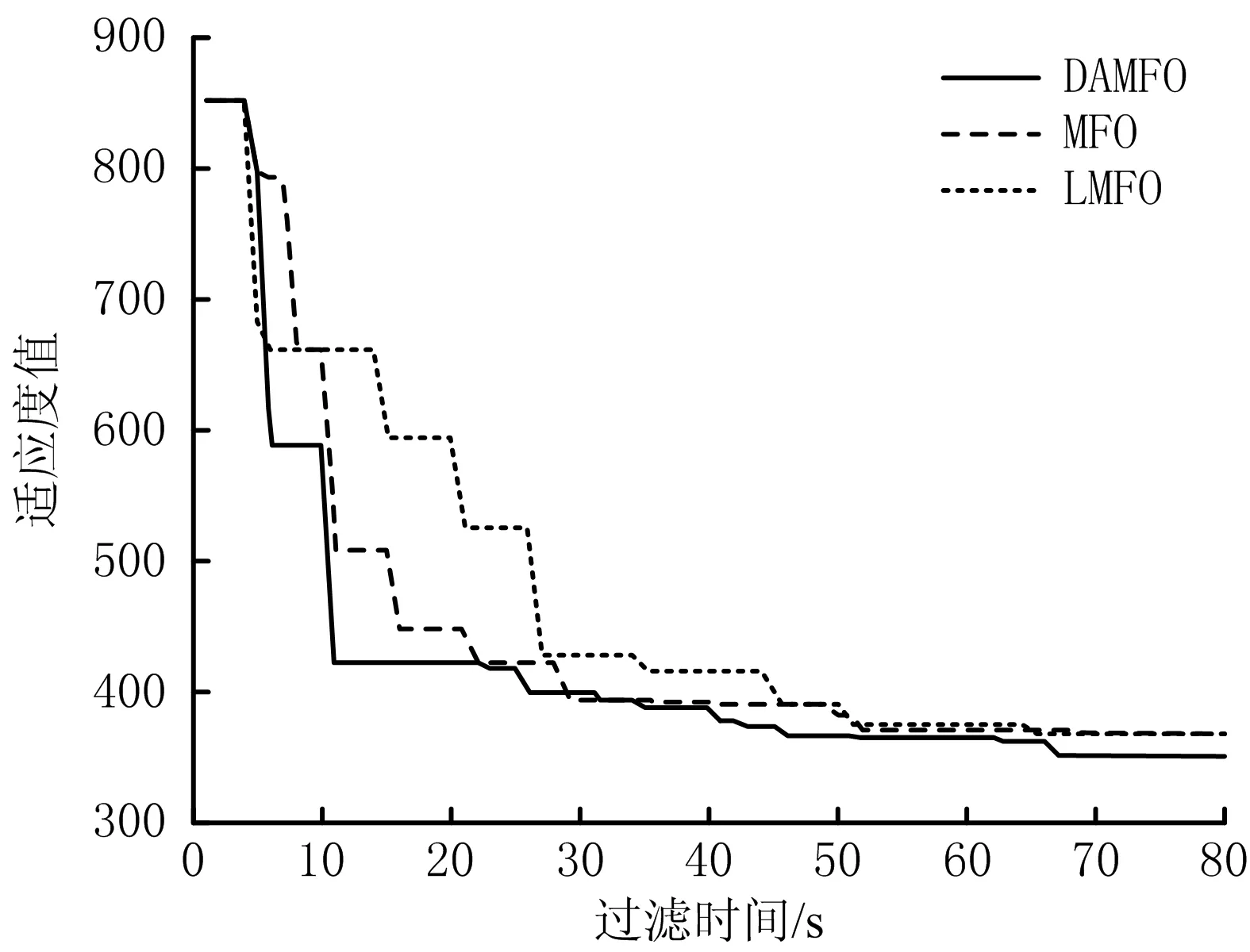
设某城市有n个应急资源储备点(A1,A2,…,An),有m个受灾点(B1,B2,…,Bm),储备点提供p种物资(C1,C2,…,Cp)。设aqi表示第q种应急物资在第i个储备点的储存量,bqj表示第j个受灾点对第q种应急物资的需求量(1≤i≤n,1≤j≤m,1≤q≤p)。设从第i个应急物资储备点到第j个受灾点的运输道路上,存在道路毁坏的可能性,Xij表示道路毁坏的距离,T0表示单位距离下修复毁坏道路的时间,Tend表示修复毁坏道路的最晚修复时间。设0≤α<β表示道路正常通行;β≤α<δ表示道路毁坏,需要修复,若修复时间T0Xij 假设储备点应急物资总量、运输车辆足够,受灾点对每种应急物资的需求度、每辆车运输速速一致,最短运输路线只有1条且运输路况只能是道路正常、道路毁坏可修复或道路毁坏不可修复、道路毁坏不可通行中的1种。 1)飞蛾扑火优化算法 飞蛾扑火优化(MFO)算法主要灵感来自飞蛾的定向水平飞行方式。MFO算法具有的特殊结构,在低维时能够更好地协调局部和全局的搜索能力,使其不容易陷入局部极值而找到最优解,但在高维每次迭代中都会选取当前最优解,容易陷入局部最优而导致过早收敛,由于种群多样性低,使得全局寻优性能不高。 2)基于Levy飞行的飞蛾扑火优化算法 基于Levy飞行的飞蛾扑火优化(LMFO)算法在MFO算法的基础上增加了1个随机扰动,该随机扰动被称为Levy飞行。Levy飞行的突出特点是大量小步移动,偶尔有较大步移动,这样飞蛾就不会在1个地方一直重复搜索,进而改变1个系统的行为。对飞蛾群执行1次Levy飞行,如式(1)~(4)所示。 飞蛾实时位置如式(1)所示: (1) Levy的分布如式(2)所示: Levy(β)~u=t-β(1<β<3) (2) Levy(β)的随机数如式(3)所示: (3) 式中:u和v服从标准正态分布;Ø是正态分布的方差,如式(4)所示: (4) 式中:Γ是1个标准的伽码函数;β=1.5。 3)模型建立 经典MFO算法需要给定飞蛾位置的上下边界,边界条件是飞蛾位置的线性组合,无法直接获得。为解决此问题,以运输过程中消耗成本最低、物资装车时间最少为优化目标,引入变量归一化约束条件作为惩罚项,建立如下模型如式(5)~(14)所示: (5) (6) s.t. (7) (8) (9) (10) (11) (12) (13) (14) MFO算法和LMFO算法均使用对数螺旋函数更新飞蛾位置,使飞蛾容易陷入局部最优,另外MFO算法中,无论是迭代初期还是迭代后期,飞蛾向火焰飞行的速度一致,无法获得全局最优解。因此,本文提出基于双自适应因子的改进MFO算法DAMFO。该算法在MFO算法或LMFO算法的基础上做了如下改进: 1)增加自适应权值因子,提升初期全局搜索能力。原飞蛾位置更新公式如式(15)~(16)所示: S(Mi,Fj)=Diexp(bt)×cos(2πt)+W0Fj (15) (16) 式中:W0为自适应权值因子;li为当前迭代次数;lM为最大迭代次数。随迭代进行,自适应权值逐渐变小,飞蛾拥有更强的跳出局部最优解的能力。 2)增加自适应速度因子,减缓迭代初期飞行速度,加快迭代后期收敛速度。原飞蛾位置更新公式中的t参数可由式(17)~(18)随机产生: t=rand([W1,-1]) (17) (18) 式中:rand([a,b])函数表示在区间[a,b]间均匀产生1个随机数;自适应速度因子W1表示通过该方法,在迭代后期t生成较小值的概率更高,从而加速整个系统的收敛。 3)改进种群初始化方法,提高初始种群质量。 步骤2:针对每组q,j,计算差值如式(19)所示: (19) (20) 假设在某地区发生地震灾害,出现2个受灾点B1,B2,该地区应急资源储备点共有5个A1,A2,A3,A4,A5。受灾点需要储备点提供的应急物资共有3种,分别为急救药品C1、食品C2,帐篷C3。储备点可以提供的各种应急物资数量和受灾点需要的各种应急物资数量见表1。车辆在储备点到受灾点的路途中运输单位物资量所产生的成本C,见表2。各物资在储备点的单位装车时间见表3。储备点至受灾点的交通道路损毁距离Xij和相应损毁程度系数α见表4~5。设当0≤α≤0.2,表示交通道路可以通行,不需要工人对道路进行施工修复;当0.2<α<0.7,表示交通道路可以修复,设单位距离下修复毁坏道路的时间为0.5 h(即T0=0.5 h),最长修复时间不得超过3 h(即Tend=3 h),当修复时间T0Xij 表1 储备点提供的物资数量及受灾点需要的物资数量 表2 储备点各物资的单位运输量成本 表3 各物资在储备点装车时间 表4 储备点至受灾点的道路损毁距离 表5 储备点至受灾点的道路损毁程度系数 设置时间成本系数θ为1,权重系数满足w1+w2=1。根据专家评价法,分析运输成本权重w1为1/4,时间成本权重w2为3/4,即对应急资源调度配置方案来说,应急物资装车时间成本比运输成本更重要。MFO算法、LMFO算法和DAMFO算法的参数设置如下:飞蛾群体数为500个,最大迭代次数为500,个体位置信息的维度根据算例中5个储备点对2个受灾点提供的3种应急物资确定为30,LMFO算法和采用Levy飞行的DAMFO算法中乘数因子设置为0.05。 为验证算法的有效性,主要比对随机种群初始化场景下和改进种群初始化场景下的MFO算法、LMFO算法和DAMFO算法在求解应急资源调度优化模型下的寻优性能。为了公平性,上述算法测试时均采用相同的飞蛾初始种群,即在迭代开始前拥有相同的适应度值。 1)随机种群初始化场景下,xqij在[0,1]范围内均匀分布,MFO算法、LMFO算法、DAMFO算法的收敛速度、适应度如图1~2所示。 图1 收敛速度比较 由图1可知,在迭代初期,DAMFO算法的收敛速度相对最快,MFO算法次之,LMFO算法最慢。这是由于LMFO算法增加了Levy飞行,以期在寻优初期跳出局部最优点而找到全局最优值,但也明显拖累整个算法的收敛速度。由图2可知,在迭代后期,DAMFO算法获得更好的性能,具有相对最低的适应度值;MFO算法直接陷入局部最优点;而LMFO算法在迭代375次之后跳出局部最优点,适应度值大幅下降,但性能仍低于DAMFO算法。 图2 收敛性能比较 2)改进种群初始化场景下,飞蛾初始种群出现在全局最优点附近的比例得到有效提升,在迭代寻优过程中能更快地找到全局最优点。在迭代寻优初期,未采用Levy飞行的MFO算法和DAMFO算法适应度值快速下降,DAMFO算法虽然在前期增加全局搜索能力,但其收敛性能与MFO算法旗鼓相当。在迭代后期,未采用Levy飞行的DAMFO算法逐渐收敛,而其他算法仍需更多迭代次数才能收敛至全局最优点。另外,由于采用快速收敛机制,即使采用Levy飞行的DAMFO算法也获得和MFO算法相似的性能,远远优于LMFO算法性能,这也说明LMFO算法在该场景中并不一定提升全局最优搜索能力。 3)使用不同算法求解得到的最终适应度值见表6,在随机均匀种群初始化场景下适应度值为851.01,改进种群初始化场景下适应度值为360.92。由表6可知,当采用特殊初始化种群方法后,MFO算法、LMFO算法和DAMFO算法均有效提升最终收敛性能。 表6 最终适应度值 4)MFO算法和DAMFO算法的最优调度方案见表7。由式(13)计算可得,当道路无损坏时,MFO算法和DAMFO算法的单目标函数值minf分别为309.3,308.75,后者在装车时间及运载成本方面节约55%;当道路有损坏时,MFO算法和DAMFO算法的单目标函数值minf为328.55,328.252 5,后者在装车时间及运载成本方面节约了29.75%。分析得出无论是否存在道路损坏情况,DAMFO算法的最优方案均优于MFO算法的最优方案,在合理调配应急资源和节约装车时间、运载成本方面表现出更大优势。 表7 MFO/DAMFO算法的最优调度方案 1)针对灾害事故发生后,为解决制定及时、有效的多灾害点应急资源调度方案问题,将应急资源在不同运输路况下运输的最低消耗成本、最少装车时间作为优化目标,引入变量归一化和约束条件作为惩罚项,构建应急资源调度模型。 2)提出基于双自适应因子的改进MFO算法DAMFO,增加自适应权值因子,提升初期全局搜索能力;增加自适应速度因子,加快迭代后期收敛速度。 3)仿真结果显示,DAMFO算法有效改善MFO算法和LMFO算法的寻优性能等问题,在求解模型时能够提供精确度、满意度更高的应急资源调度方案,具有较高的应用价值。1.2 条件假设
1.3 模型建立


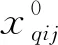
2 改进飞蛾扑火算法
3 算例分析
3.1 算例描述




3.2 仿真结果



4 结论

