基于MAC法的空间太阳能电站传感器优化配置与参数辨识
张宇航,倪智宇
(沈阳航空航天大学 航空宇航学院,沈阳 110136)
空间太阳能电站(Space solar power station,SSPS)概念的提出,将改变太阳能的获取和传输方式,以解决能源危机,保障国家能源安全[1]。SSPS为了保证太阳能的高效收集与转换传输,往往设计为特征尺寸在百米乃至千米量级的空间结构,这种大尺寸、低刚度的结构特点使得系统具有较高的挠性、较低的振动频率且动态特性复杂,是一种典型的大型挠性航天结构。对于SSPS这类大型空间结构,利用参数辨识方法获取其在轨精确的模态信息(频率、阻尼比等),可以为振动控制系统设计、姿态指向稳定性研究、动力学模型修正以及损伤预测和动态载荷识别等诸多方面提供重要参考,具有较高的应用价值。
为了对SSPS进行在轨模态辨识,通常需要对其配置加速度计或位移传感器以测量结构的振动响应,而传感器获取的振动信号与航天结构实际振型的匹配度将直接影响模态参数在轨辨识的准确性[2]。由于空间太阳能电站结构复杂、自由度较多,考虑制造成本、载荷要求及可靠性等因素,在轨监测过程中可以布置传感器的测点数会远远小于结构的自由度数,则寻找合理的传感器数目是布设传感器的前提条件。此外,由于受传感器数目的限制,不可能获取航天器全部自由度上的信息,如何将有限数目的传感器分布于信息量较大、对各阶模态的区分贡献较大的测点,也是保证量测信息准确反映被测航天器振动特性的关键之一。因此,利用合适的优化方法与评价准则对传感器的数目与布置点位进行优化,对于准确地识别结构的模态参数进而有效地对大型挠性航天器进行控制具有重要的现实意义[3]。
近年来,国内外学者在工程结构的振测传感器布置研究方面做了大量开拓性工作。Kammer[4]首先提出了有效独立性方法(Effective Independence,EI),使目标模态向量在较少测点的情况下,尽可能保证线性独立性。EI方法作为一种著名的传感器配置方法,已经在工程结构中得到了广泛的应用[5-6]。文献[7]中提出了模态动能法(Modal Kinetic Energy,MKE),选择模态动能较大的节点作为优先配置点。崔飞等[8]提出了模态置信度法(Modal Assurance Criterion,MAC),首先根据经验和初算来拟定一组测点,然后从剩余的模型自由度中每次增加一个测点,并以减小模态置信度矩阵中非对角元的最大值作为目标,来达到传感器布点优化的目的。在工程应用的探索方面,管林挺等[9]基于EI法对高铁受电弓的不同部件分别进行了传感器优化配置,具有工程指导意义;苗壮[10]针对20 m口径的索网式可展开星载天线,组合应用改进的有效独立法与基于QR分解的逐步累积法,弥补了两种子方法的缺点;杨拓[11]在传感器优化配置中结合改进的遗传算法,在东方红3号卫星太阳帆板模型中进行了配置,为实际工程应用提供了更多选择。文献[12]基于EI法与三维冗余消去模型对简单空间桁架结构进行传感器优化配置,改善了传感器聚集产生的信息冗余问题。
在对航天领域实际工程应用对象的研究中,多数学者针对航天器所携带的小尺寸柔性附件(例如太阳能帆板等)进行传感器的优化配置研究,少有学者涉猎空间太阳能电站这类具有大尺寸、大挠性特点的空间结构。而对传感器数目进行优化并应用参数辨识方法对优势方案进行验证的工作也较为少见。由于大尺寸、大挠性将是未来航天器发展的主流方向,对其开展传感器优化配置的研究具有重要的现实意义,因此本文针对SSPS的振动传感器布置问题,力求寻找解决方案。首先,依托多种评价准则,综合成本、容错性等因素,探寻适宜采用的传感器配置数目;其次应用评价准则的各项指标对基于MAC法所得方案与经典的EI法、MKE法所得方案进行对比分析;最后利用经典的特征系统实现参数辨识算法(Eigensystem Realization Algorithm,ERA)[13]对模态置信法所得方案进行验证。仿真结果表明,针对SSPS这类具有超大尺寸的大型挠性空间结构,利用MAC法得到的传感器优化配置方案模态区分度的优势较为突出,目标模态参数的辨识具有令人满意的计算精度,更加适合于解决SSPS的振动传感器布置问题,对未来工程应用具有一定的参考价值。
1 传感器优化配置方法及评价准则
1.1 3种常用的传感器优化配置方法
1.1.1 模态置信法(MAC)
MAC法是基于模态置信度准则而提出的。根据结构动力学原理,结构完备的模态振型向量应为一组相互正交向量。实际工况下,由于传感器数目相较于结构自由度数目较小,且存在噪声影响,所测得的模态振型向量难以保证良好的正交性,而模态置信法的核心思想则是避免采集到的模态振型向量因为空间交角过小而损失重要信息。
首先,设空间太阳能电站的动力响应方程为
(1)
其中:X为空间太阳能电站位移响应的理论值;Φ为有限元建模得到的n×m阶模态矩阵;n为系统全部自由度;m为目标模态阶数;q为广义坐标。模态置信度矩阵定义为
(2)
其中:Φi和Φj分别为第i、j阶振型列向量;当Cij=0且i≠j时,说明第i阶列向量与第j阶列向量的空间夹角为90°,即考察C矩阵的非主对角线元素,其最大值越小则测得的模态向量间线性独立性越高,模态的可分辨性越好。
应用模态置信法时,首先依据经验或者其他算法初选少量传感器布置点位,形成初始自由度集合;其次,将剩余待测自由度分别加入初始自由度集合中,依次计算各个集合的C矩阵,并记录最大非对角元的数值,选取该数值最小的集合作为新的初始自由度集合;最后,进行迭代计算,直至集合中包含与传感器数目相同的自由度数,即获得传感器优化配置方案。本文在应用MAC法时,初始传感器布置点位采用有效独立法计算获得[14]。
1.1.2 有效独立法(EI)
EI法最早由Kammer等人在研究针对大型空间结构的传感器优化配置问题时提出,这种方法的主要思想是从全部的可测自由度出发,逐步删除对模态线性独立贡献最小的待测自由度,进而优化Fisher信息阵,最终获得传感器优化配置方案。以期在较少测点的情况下尽可能保持模态向量的线性无关。该方法通过求解矩阵ΦTΦ(Fisher信息阵的等价矩阵)的特征方程,构建有效独立矩阵
E=Φψλ-1ψTΦT=Φ(ΦTΦ)-1ΦT
(3)
其中:ψ是矩阵ΦTΦ的特征向量矩阵;λ是矩阵ΦTΦ的特征值矩阵。矩阵E为幂等矩阵,其主对角线上元素在0~1之间,各个元素的大小反映了对应自由度对目标模态线性独立性贡献的大小。应用有效独立法时,对矩阵E的主对角元排序,删除最小元素所对应的自由度,构建新的模态矩阵依次迭代,直至自由度数目与传感器数目相同,得到传感器优化配置方案。
1.1.3 模态动能法(MKE)
MKE法的提出是基于传统的依靠主观经验选取结构振动幅值较大的点布放传感器的方法,它的核心思想是获得模态动能较大的测点信息更利于提高测量时的信噪比,在噪声环境中提高抗干扰能力。
模态动能的大小由结构的模态矩阵与质量矩阵共同作用,定义Ki为模态动能矩阵的第i阶列向量,其表达式为
Ki=Φi*(MΦi)
(4)
其中:Φi为模态矩阵第i阶列向量;M为质量矩阵;符号*表示矩阵做点乘运算,即两侧矩阵对应位置的元素相乘。得到模态动能矩阵后,对其按行求和即可得到各个自由度相应的模态动能。应用MKE法时,即根据模态动能列向量,依照模态动能降序排列,依次选取与传感器数目相同的自由度,完成传感器的优化配置。
1.2 方案评价准则
评判上述优化方法的传感器配置方案是否适用于相应的结构对象,需要依靠相应的评价准则,下面简要列举本文所采用的4个准则。
1.2.1 模态动能准则
由于结构的模态动能在各阶模态和各个自由度上的分配都是不均匀的,因此模态动能准则希望方案选取的传感器测点包含较大的能量,以保证测试信号具有较强的抗干扰性。提高模态识别精度,即如果传感器布点的总模态动能越高,则对应的传感器优化配置方案越优。
1.2.2 Fisher信息矩阵准则
为了获得广义坐标q的最佳估计,即最小化q的估计偏差,需要最大化Fisher信息阵的迹或行列式的值。同时,Fisher信息阵也度量了测得的振动响应中所包含信息的多少,在该准则中,如果信息阵的行列式和迹越大,则传感器布置方案越优。
1.2.3 模态置信度准则
应用模态置信度矩阵来判断振型的正交性是一种较为直观且易操作的方法。该矩阵各项反映了各阶振型列向量之间的夹角余弦,值越接近于零说明空间交角越大。故为了提高实测模态的线性独立性,C矩阵的非主对角线元素的最大值越小,则传感器配置方案越优。
1.2.4 最大奇异值比准则
定义Φs为测量得到的模态矩阵,对其进行奇异值分解,存在酉矩阵U与酉矩阵V使得
UTΦsV=diag(σ1,σ2,…,σr)
(5)
其中:σ1,σ2,…,σr为矩阵Φs的奇异值;存在σm和σn分别为非零奇异值的最大值与最小值,定义二者的比值SVR(Singular Value Ratio)为评价指标,即
(6)
SVR的值越小则各阶模态线性独立性越好;计算模态扩阶结果时误差越小,模态可观性越好。因为最大奇异值比下限为1,所以SVR的值越接近于1,传感器布置方案越优。
2 空间太阳能电站传感器优化配置
2.1 模型描述与模态分析
将图1所示的SSPS构型[15]简化为四边自由的,满足基尔霍夫假设的方形薄板模型。应用Patran软件对薄板进行模态分析,模型相邻节点间的距离为40 m,共2 601个节点,有限元建模采用Shell单元类型,有限元分析示意图如图2所示。模型的几何特性和质量特性如表1所示,选取前10阶弹性模态作为目标模态,各阶模态振型及频率如图3所示。

图3 空间太阳能电站有限元计算振型及频率

表1 空间太阳能电站模型的几何及质量特性
图1 SSPS构型概念图

图2 空间太阳能电站有限元模型
2.2 传感器优化配置方案
根据系统可观性原则,传感器个数至少应等于选取的模态阶数,但考虑SSPS结构尺寸较大,待测自由度较多,故需参考传感器优化配置准则的各项性能指标,寻找相应的最优传感器数目。这里除了使用MAC法之外,还采用EI法和MKE法进行优化配置结果的比较,3种优化配置算法所得到的布置2~50个传感器时,各方案的模态动能的值和信息阵的迹值如图4所示。由图4可见,因为模态动能指标与信息阵的迹指标反映的是所布置传感器获取到的结构能量大小与振动响应中包含信息的多少,所以这2个指标的值是随着传感器数目的增加而近似均匀增加的,在寻找各个方法的最优传感器数目时,这2个指标不做参考。

图4 各方案不同传感器数目模态动能和信息阵的迹
应用MAC法配置不同数目传感器时,各数目方案的最大非对角元和最大奇异值比如图5所示。根据评价准则要求,最大非对角元越趋近于0、最大奇异值比越趋近于1,则方案的模态区分度越好。观察图5可以看出,当传感器数目大于24个之后,两项性能指标均趋于平稳且较优。为了节约成本,选用布置24个传感器时的方案作为模态置信法,最终得出传感器优化配置方案。

图5 MAC法配置不同数目传感器最大非对角元和最大奇异值比
应用EI法配置不同数目传感器时,各数目方案的最大非对角元和最大奇异值比如图6所示。从图6中可以看出,当配置传感器数目为12、24、36和48个时均为较优解。综合考虑传感器系统容错性与安装成本,便于横向比较,取布置24个传感器时的方案作为有效独立法,最终得出传感器优化配置方案。
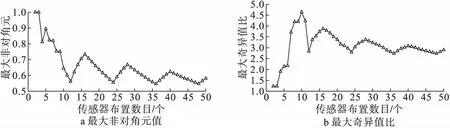
图6 EI法配置不同数目传感器的最大非对角元和最大奇异值比
应用MKE法配置不同数目传感器时,各数目方案的最大非对角元和最大奇异值比如图7所示。从图7中可以看出,应用模态动能法时随着传感器数目的增加,最大非对角元始终接近于1,没有明显减小的趋势;最大奇异值比保持在102量级,远高于其他2种算法,说明模态动能法在振型分辨率方面与前2种方法相比具有一定的差距。同样选取布置24个传感器时的情况作为模态动能法,最终得出传感器优化配置方案。

图7 MKE法配置不同数目传感器的最大非对角元和最大奇异值比
通过3种优化配置算法分别得到的最终测点位置如图8所示。观察图8可以发现,MKE法优先选取振幅较大的测点,出现了传感器集中的现象;EI法布置位点均匀地分布在结构边缘,但仍存在测点聚集的情况;而MAC法将传感器呈分布式布置在整个结构上,有效地减小了配置冗余性,可以更加客观地反映结构整体的振型与振幅,更适宜应用于SSPS振动信号的获取。

图8 3种方法的最终传感器优化配置位点
3 优化方案评价与验证
3.1 应用准则评价
下面通过4个评价准则对以上3种优化配置算法得到的最终传感器布置方案进行对比分析,结果如表2所示。观察表2可以发现,不同传感器配置方案各项评价指标相差较大,证明应用准则评价讨论是有意义的。而各方案的C矩阵直方图如图9所示,通常当Cij值小于0.25时,可认为模态振型向量是相互正交的;当Cij的值大于0.9时,认为模态振型向量间相互关联。

图9 3种方案的C矩阵直方图

表2 配置24个传感器时3种方案的评价
从表2中可以看出,针对MKE法所得方案,观察其信息阵的迹与总模态动能2项指标,发现MKE法善于捕获信息量较大的测点,但该优势并不明显。而最大非对角元、最大奇异值比2项指标数值相较其他2种方法差距较大,且最大非对角元大于0.9,无法保证振型的区分度,不适用于空间太阳能电站这类对辨识精度要求较高的对象。
此外,通过观察表2中EI法所得方案的评价结果,发现其各项指标均处于另外2种方法之间,对振型有一定分辨性,但最大非对角元仍大于0.25,存在所获得的截断模态向量线性独立性不足的问题。
最后,通过观察表2中MAC法所得方案的评价结果可以发现,其信息阵的迹和总模态动能均较小,说明该方案适用于环境噪声较小的工况。同时可以看出,该方案的C矩阵最大非对角元以及奇异值比两项指标与其他方案相比明显占优。图9中的直方图显示其各模态间Cij值均远小于0.25,说明MAC法所得方案最具有保持振型正交性的优势,可以应用于对辨识精度要求较高的工况,在针对空间太阳能电站在轨运行状态选取振动传感器布置方案时可优先考虑。
3.2 应用辨识结果验证
要验证MAC法所得方案对各阶模态的区分度,可以利用优化配置方法得到的结果进行参数辨识,从工程应用的角度出发,分析辨识出各阶模态与有限元分析所得数值的差距。本文采用常用于辨识机械结构、空天装备振动特性的ERA算法对空间太阳能电站模型进行模态参数辨识,以验证传感器布置方案的性能。
在仿真中,SSPS推进器的位置如图10所示,用于模拟空间太阳能电站进行对日指向调整。在具体实施过程中,分别进行绕滚转轴(X轴)与绕俯仰轴(Y轴)的姿态调节,为了不改变SSPS的轨道运动,需要推进器配合产生控制力偶,同时保证姿态角变化在5°左右,以满足动力学方程线性化条件。故设计各推进器产生的推力如图11所示,以此作为模态参数辨识的输入信号,而空间太阳能电站的姿态角信号和振动信号输出如图12所示。

图10 SSPS模型的推进器位置
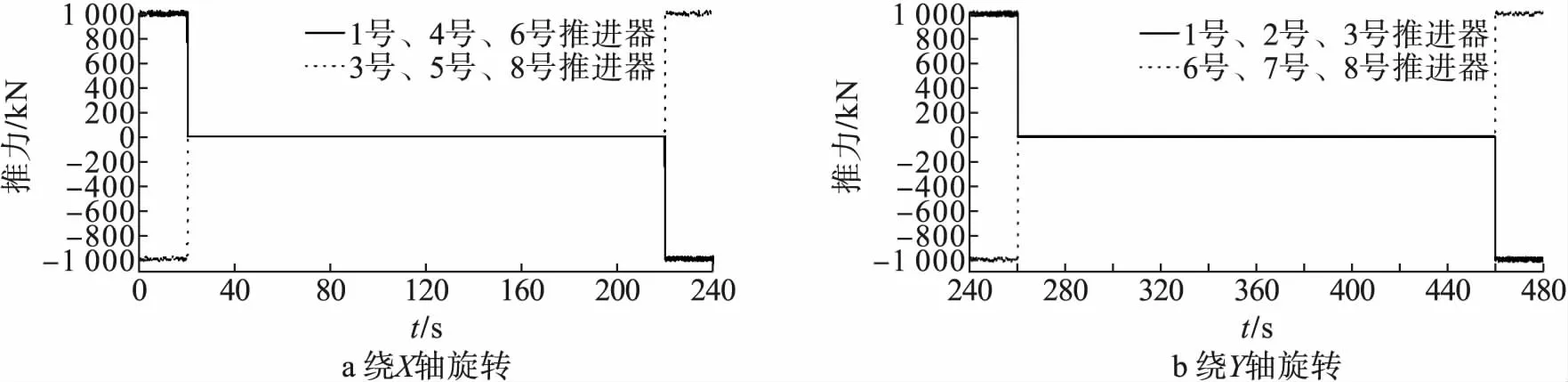
图11 SSPS姿态调整时推进器的推力值
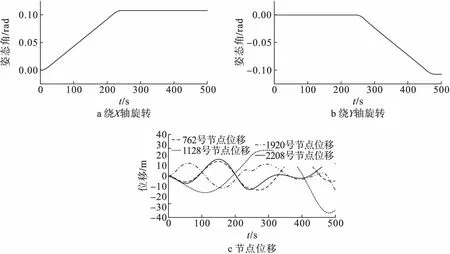
图12 SSPS的输出响应曲线
通过ERA辨识算法的计算,得到Hankel矩阵奇异值截断曲线如图13所示,得到空间太阳能电站前10阶弹性模态频率的辨识结果如表3所示。
在状态空间形式下,待辨识的系统阶次是26阶,包括6个刚体频率值与10组共轭弹性频率值。观察图13可以发现,Hankel矩阵奇异值截断点为24,该奇异值曲线的截断划分了信号空间与噪声空间,即理论模型中的26个频率值中有24个被有效辨识,即有一对共轭频率值未被识别出。同时,从表3的计算结果可以看出,选取的空间太阳能电站前10阶弹性模态频率,有9阶可以被辨识出,误差控制在1‰以内,这也证明了图13中的奇异值截断是准确的。通过ERA方法对模态频率的辨识,该计算结果充分证明了MAC法所得传感器优化配置方案模态区分度较好,应用于SSPS参数辨识时精度较高。

图13 Hankel矩阵奇异值截断曲线
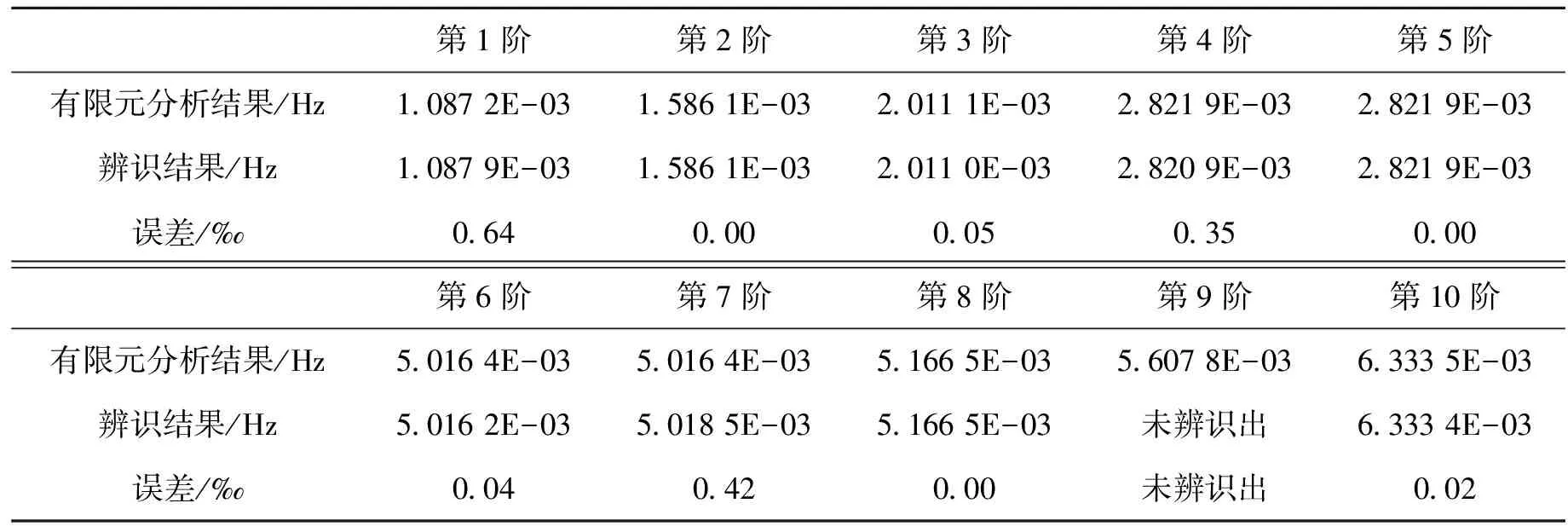
表3 模态频率辨识结果
4 结论
本文针对SSPS这类大尺寸、大挠性的空间结构,应用MAC法对其进行传感器优化配置研究,并与经典的EI法和MKE法所得方案进行对比,分析3种方法在传感器数目相同时布设方案的区别,并进行了效果评价。主要结论如下:
(1)运用模态保证准则、最大奇异值比、Fisher信息矩阵的迹和总模态动能准则对3种传感器配置方案进行全面的对比评价,结果表明,与EI法和MKE法所得方案相比,MAC法方案的测点分布最能保证模态之间的正交性与可观性。同时MAC法方案测点最为分散,可以较好地避免信息冗余,为空间太阳能电站的模态参数辨识工作提供较为准确的输出信号。
(2)设计阶跃信号为系统输入,按MAC法方案布置传感器获取振动输出信号,运用ERA算法对空间太阳能电站的前10阶弹性模态频率进行辨识,精准地得到了其中9阶的频率值,证明了将MAC法得到的传感器优化配置方案用于振动信号获取可以使SSPS的模态参数辨识得到令人满意的结果,对未来的工程应用具有一定的参考价值。
此外,在辨识仿真结果中,存在着一阶未辨识出的弹性模态频率值,这说明对该系统前几阶的模态信息未能完全获取,其中可能的原因之一是SSPS的推进器安装在了该阶模态振型中振幅较小的位置,即未考虑作动器的优化配置问题。因此如何通过对SSPS的作动器进行优化配置以充分激发系统的模态响应来提高辨识精度,是未来值得进一步研究的问题。

