一种基于代表参数的图聚类算法

夏秀峰，方 鹏，周大海，安云哲，吴东翰，张学鑫

(沈阳航空航天大学 计算机学院，沈阳 110136)

本文研究面向大规模图的聚类问题。给定图G(V,E),V为图的顶点集合，E为图的边集合。图聚类是将图G划分成一组子图{G1,G2,…,Gn}。给定任意子图Gi(Vi,Ei)，Gj(Vj,Ej),它们满足Vi∩Vj=Ø,Ei∩Ej=Ø。此外，给定子图Gi中顶点vi,它与Gi中多个顶点存在边，而与其他子图中顶点不存在边或仅存在少量边。

图聚类问题在社区检测、模式识别、生物网络以及异常值检测等方面具有广泛应用[1-3]。如图1中所示，{s1,s2，…，s10}为10名学生，他们构成了图中的顶点集合。对于任意2个学生si和sj，如果他们所修课程相同，则他们之间存在一条边。显然，{s1,s2,s3,s4}这4名同学对某一学科兴趣程度较高，他们被划分到同一个子图G1中。同理，{s6,s7,s8,s9}这4名同学对另一学科兴趣程度较高，他们被划分到子图G2中。这样一来，当为学生推荐课外书籍时，推荐系统可根据s1所购买的图书为s2,s3,s4进行推荐。相似地，推荐系统可根据s6所购买的图书为s7,s8,s9进行推荐。

图1 学生购书推荐系统

鉴于图聚类问题的重要性，许多学者针对图聚类问题展开研究，常见算法包括k-core算法、k-dege算法、k-truss算法等[4-6]。在众多研究成果中，最具代表性的算法为Chang等人[4]提出的基于顶点特征的pSCAN算法，该算法的核心思想是根据σ(u,v)来评估各顶点间的相似性。在这里，u和v表示图数据中的顶点。现有算法的核心思想是：首先计算各顶点间的相似性，然后比较顶点间的相似性与给定相似性阈值的大小，最后按照给定的图的最小规模阈值进行聚类。基于该定义得到的划分结果可以有效实现图的聚类。然而，现有算法需要计算每2个顶点间的相似性，导致了较高的计算代价。

鉴于此，本文提出一种基于代表参数的图聚类处理框架RPGC(Representative Parameter Graph Cluster)。它的核心思想是选取一组代表性强的参数集合H{(σ1,μ1),(σ2,μ2)，…，(σm,μm)},分别计算基于这组参数的聚类结果。当有新的聚类请求Q(σq,μq)到达时，算法可根据Q(σq,μq)的值在H中找到与之相似性最高的元组(σsim,μsim)，进而根据(σsim,μsim)的聚类结果快速计算基于(σq,μq)的聚类结果。和前人所提算法相比，RPGC计算框架下的算法有效利用历史聚类结果实现新聚类请求的快速响应。主要贡献如下：

(1)提出一种基于二部图的代表参数选取算法。该算法首先将一组代表参数映射到网格G内。以此为基础，算法针对每个代表参数执行范围查询，并根据聚类参数和结果之间的关系构建二部图。最后利用贪心算法实现代表性参数的选取。

(2)提出一种基于代表参数的图结构增量聚类算法。该算法的核心思想是找到与查询参数相似性高的代表参数，根据代表参数和查询参数之间的关系降低顶点间相似性关系的计算频率，进而降低整体计算代价。

1 研究现状及问题定义

1.1 研究现状

现有图聚类算法主要分成2种类型：第一种是基于模块化或者基于密度的聚类方式，这种类型的图聚类算法不考虑被聚类的顶点之外的顶点，如上文中所提到k-core算法、k-edge算法、k-truss算法等。此类算法的问题是破坏了图结构的完整性；第二种类型是基于顶点角色的聚类方式，主要包括SCAN算法，SCAN++算法和pSCAN算法等[7-9]。它们的核心思想都是把顶点划分到经聚类得到的子图中。

SCAN算法反复处理没有被分配到任何簇中的顶点。如果一个顶点被当做核心顶点，并且它与其他簇中的核心顶点之间不存在边，SCAN算法就会为该顶点生成一个新的簇。该算法的缺点是必须计算图G中的每一对相邻顶点间的结构相似性。SCAN++算法则避免了计算2个较远顶点间的结构相似性。然而，该算法对图的规模很敏感，不适合计算规模较大的图。pSCAN算法通过剪枝和连接等方式降低了计算顶点间结构相似性的成本，并有效加快了计算速度。但以上算法均未提前存储簇类结果，每次都需要重新计算顶点间的相似性，这种方式需要的计算时间较长[10]。

1.2 问题定义

本文主要研究无向无权重图的图聚类问题。给定图G中顶点u和v，如果u和v之间存在一条边，则称v为u的邻居，u也被称为v的邻居。

定义1(结构化邻居)对于图G(V,E)中的任意顶点,其结构化邻居的定义为N[u]={v∈V|(u,v)∈E}∪{u}。如果顶点u拥有d(u)个结构化邻居，那么顶点u的度为d(u)。

定义2(结构相似性)在给定的图G中，如果存在任意2个顶点u,v∈V，则可将顶点u,v的结构相似性表示为

(1)

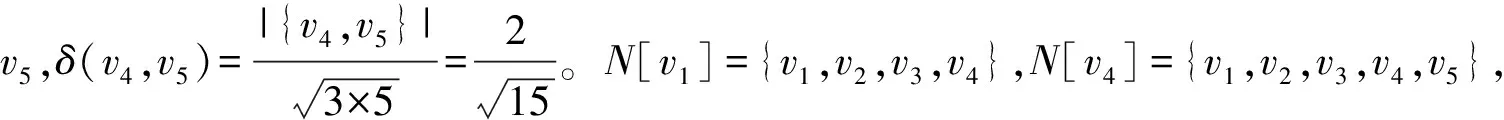
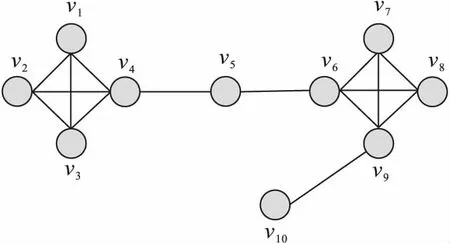
图2 图聚类示意图

定义3(核心顶点)给定2个参数阈值σ和μ，0≤σ≤1,μ≥2。对于图中顶点u，当Nσ[u]≥μ时，u被称为核心顶点。否则，u被称为非核心顶点。特别地，假设v是一个簇Gi中的核心顶点，如果G中的顶点v′满足δ(v,v′)≥σ，v′将会被视作Gi中的元素。如果顶点v被视为Gi中的元素，它需满足如下条件之一：(1)v是Gi中的核心顶点；(2)Gi中存在核心顶点v′满足δ(v,v′)≥σ。

定义4(离群点)给定图G和2个参数σ和μ，{C1,C2,…,Cn}是一组在阈值范围内的核心簇集合，对于每一个顶点u∈G，如果该顶点不属于任意一个簇，并且只和不多于一个簇相连接，则该顶点被称为离群点。

定义5(桥结点)给定图G和2个参数σ和μ，{C1,C2,…,Cn}是一组在阈值范围内的核心簇集合。对于每一个顶点u∈G，如果该顶点不属于任意一个簇，但和不少于2个簇相连，则该顶点被称为桥结点。

定义6(簇)簇C是不少于2个顶点V(|C|≥2)构成的集合,它具有如下特性：(1)如果一个核心顶点u∈C，那么C中所有顶点都和顶点u结构可达。(2)对于任意的2个顶点v1,v2∈C，如果存在一定顶点u∈C，那么顶点u和顶点v1,v2结构可达。

如图2所示，给定相似性阈值ε=0.8,μ=4，图2中的顶点可被划分到2个簇C1={v1,v2,v3,v4}和C2={v6,v7,v8,v9}。

需要注意的是：给定一个核心顶点v∈Ci，对于其它顶点v′，如果δ(v,v′)≥σ，那么v′也是Ci中的元素。换句话说，如果一个顶点是Ci中的元素，那么存在Ci中的核心顶点与该顶点之间的结构相似性不小于σ，或者该顶点必然是核心顶点[11]。

定义7(问题描述)设σ和μ是2个阈值，且满足0≤σ≤1，μ≥2。图聚类是将图G(V,E)划分成一组簇{C1,C2,…Cm}、桥结点和离群点的集合。对于每一个顶点v∈Ci，要么该顶点v是核心顶点，要么存在另外一个核心顶点v′∈Ci与顶点v之间的结构相似性不小于阈值σ。如图2所示，假设参数的阈值为σ=0.8,μ=4，则图G可以被划分成2个簇C1={v1,v2,v3,v4},C={v6,v7,v8,v9}。此外，v5为桥结点，v10为离群点。

2 基于代表参数的图聚类算法

本文主要研究基于代表参数的图聚类算法。正如前文所述，该算法提前构建一组代表性强的参数RH{(σ1,μ1),(σ2,μ2)，…，(σm,μm)}集合，使用算法pSCAN分别基于这组参数计算聚类结果[12]。当新聚类任务参数Q(σq,μq)被提交时，RPGC首先在参数集合H中找到与之相似程度最高的一组参数<σi,μi>。利用<σi,μi>下得到的聚类结果，增量地计算参数Q(σq,μq)下的聚类结果。

2.1 代表参数集选取算法

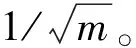
算法1：参数集选取算法

输入：H{(σ1,μ1),(σ2,μ2)，…，(σm,μm)}。

输出：参数集RH{(σ1,μ1),(σ2,μ2)，…，(σm,μm)}。

1.for eachiin{μ1,μ2,…,μm} do

2. find(μmax);

5.forifrom 1 tomdo

6. select(σi,μi);

7.Q{Q1,Q2,…,Qm}←pSCAN(σi,μi);

8.for eachiQ{Q1,Q2,…,Qm}

9. createBG{RH(Qi)};

10.RH(σi,μi)←wmax；

11. insert{RH(σi,μi)}；

12. returnRH{(σ1,μ1),(σ2,μ2)，…，(σm,μm)}。

如图3a所示,算法分别基于阈值{(0.2,0.3),(0.4,0.6),(0.6,0.4),(0.8,0.7)}执行范围查询。基于聚类参数阈值(0.2,0.3)得到的阈值为{G1,G5，G6}，基于阈值(0.4,0.6)得到的结果集为{G2，G5，G6}。以此为基础，算法根据查询结果构建二部图。其中，二部图的左部表示查询中心点，右部表示查询结果。给定右部某代表参数h,它的出度表示它出现在多少个查询结果集内。如图3b所示，G6的出度最高。因此，它被输出至查询结果集。随后，算法重复上述操作构建代表参数集RH。

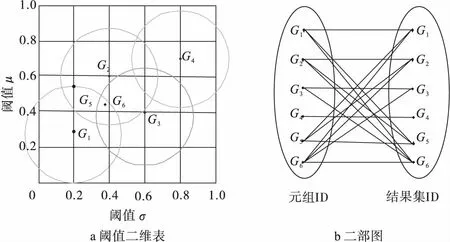
图3 阈值二维表和二分图

2.2 基于代表参数集的增量聚类算法

当有新的聚类请求q(σq,μq)提交时，算法首先在RH中找到2个历史查询(σl,μl)和(σu,μu)。其中，(σl,μl)指所有被(σq,μq)支配的参数中与(σq,μq)相似程度最高的。在这里，σl≤σq并且μl≤μq，则称(σl,μl)被(σq,μq)支配。相似地，如果σu≥σq并且μu≥μq，则称(σu,μu)支配(σq,μq)。本节引入(σl,μl)和(σu,μu)的原因在于可以利用这2组参数下的结果支持增量维护。

情况Iσq>σi,μq>μi。在这种情况下，2顶点之间具有如下性质：(1)如果二者基于(σi,μi)是不相似的，那么它基于(σq,μq)得到的结果一定是不相似的；(2)如果二者基于(σi,μi)是相似的，那么它基于(σq,μq)得到的结果可能是相似的，也可能是不相似的。这导致(1)给定G中顶点ei、ej, 如果它们在(σi,μi)下属于同一个簇，那么它们在(σq,μq)可能属于不同的簇；(2)给定G中顶点ei、ej,如果它们在(σi,μi)下不属于同一个簇，那么它们在(σq,μq)一定不属于同一个簇；(3)如果G中顶点ei在(σi,μi)下是离群点或桥结点，那么它在(σq,μq)下仍然是离群点或桥结点。

基于上述性质，增量聚类算法的核心思想是给定G中顶点ei、ej, 如果它们在(σi,μi)下不属于同一个簇，那么算法不检查它们之间的相似性[13-15]。例如：当提交任务中2个参数的值分别为0.5和8，而历史特殊点的值为0.4和6，因为0.4<0.5,且6<8,故在历史记录中不能被划分到同一个簇中的顶点，在新的任务提交后仍然不能被划分到同一个簇中，即历史记录中是离群点的仍然是离群点，而不会因为参数改变而被划分到核心顶点簇中。

情况IIσq<σi,μq<μi。在这种情况下，2顶点之间具有如下性质：(1)如果二者基于σi,μi是相似的，那么它们基于(σq,μq)也一定是相似的；(2)如果二者基于(σi,μi)是不相似的，那么它们基于(σq,μq)得到的结果可能是相似的，也可能是不相似的。这导致(1)给定G中顶点ei、ej, 如果它们在(σi,μi)下不属于同一个簇，那么它们在(σq,μq)一定不属于同一个簇；(2)给定G中顶点ei、ej, 如果它们在(σi,μi)下不属于同一个簇，那么它们在(σq,μq)一定不属于同一个簇；(3)如果G中顶点ei在(σi,μi)下是离群点或桥结点，那么它在(σq,μq)下仍然是离群点或桥结点[16]。

例如：当提交任务中2个参数的值分别为0.4和6，而历史特殊点的值为0.5和8，因为0.4<0.5,且6<8,故在历史记录中不能被划分到同一个簇中的顶点，在新的任务提交后仍然不能被划分到同一个簇中，即历史记录中是核心点的顶点此时仍然是核心点，不会因为参数改变而被划分到离群点或者桥结点的顶点簇中。

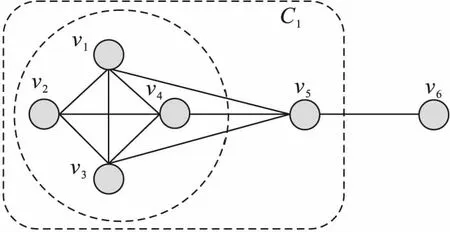
图4 图聚类示意图

算法2增量计算算法

输入：图G(V,E)数据，相似性阈值0≤σ≤1,μ≥2。

输出：图G中簇{C1,C2,…Cm}集合。

1.for vertexu∈Vdo

2.ifσq=σi,μq=μi

3. return {C1,C2,…Cm};

4.else ifσq>σi,μq>μi

5. forifrom 1 tomdo/*m is number of C*/

6.pSCAN(Ci);

7.else ifσq<σi,μq<μi

8. calculate(bridge vertex, outlier vertex);

9.then return {C1,C2,…Cm};

如上述算法所示，输入图数据以及相似性阈值，首先查找给定的相似性阈值与存储在阈值表中最接近的阈值。此时主要考虑3种情况：第一种情况，如果提交的阈值和阈值表中的阈值相等，直接数据聚类结果；第二种情况，如果提交的阈值大于与其最近的阈值表中的值，那么使用pSCAN算法找到已有阈值聚类结果，重新聚类，此时不需要计算已有的离群点和桥结点；第三种情况，如果提交的阈值小于与其最近的阈值表中的值，此时不需要重新聚类，只需要计算桥结点和离群点能否被划分到现有的集合中即可[18]。其他情况与此类似，不需详细说明。

3 实验

3.1 实验准备

(1)数据集。实验的第一个真实数据集是2003年3月通过爬取亚马逊网站商品购买关联的信息，如果某顾客购买了商品i之后，又购买了商品j，那么在i，j之间连接一条边，表示它们之间有关联。实验的第二个真实数据集LiveJournal来自于一个免费的在线博客社区，用户可以在此相互宣布友谊。LiveJournal还允许用户组成一个组，其他成员随后可以加入该组。该数据集将这些用户定义的组视为真实的社区，可提供LiveJournal友谊社交网络和真实的社区(见表1)。

表1 真实数据集

此外，实验生成了8个合成数据集(见表2)。每个数据集包含多组图数据的顶点和边，旨在探讨大规模数据集下RPGC计算框架下算法的计算时长和通信代价。

表2 合成数据集

(2)参数设置。在本实验中2个重要参数需要测试。它们是相似度阈值σ和聚类常数μ。由于参数σ的范围是0<σ≤1，但是若σ=0时，任意2个顶点都可以被聚类，对于研究顶点之间的相似性没有意义，所以舍弃。同理当σ=1时，2个顶点完全相同，对于研究顶点间相似性也没有意义。所以选取参数σ的范围是0.2～0.8，默认值是0.5；参数μ的范围是μ≥2，选取的μ的范围是4～16，默认值是10。

(3)实验方法。实验分成2组完成。第一组实验：通过数据量的不断增加来比较算法SCAN++、pSCAN、RPGC之间的运行时长。通过比较运行时长得出参数σ对各算法的影响以及优劣性。第二组实验：比较算法SCAN++、pSCAN、RPGC在不同数据集下的通信时长，以及参数μ对各算法通信时长的影响。

3.2 实验分析

(1)相似度参数σ对各算法的影响。本实验测试图聚类参数σ对聚类时长的影响。实验分别使用真实数据集和合成数据集测试，在参数σ变化的情况下，其他参数采用默认值。实验结果如图5所示。分别观察图5a～5c中的运行时间，可以看到，随着参数σ的逐渐增加，SCAN++算法的运行时间逐渐增加，而pSCAN算法和RPGC计算框架下的算法运行时间逐渐减少，RPGC计算框架下的算法平均消耗的时间仅为SCAN++的39%，pSCAN算法的66%。由于该算法提前计算产生了聚类结果，当聚类任务提交的时候，只需要按照增量计算便可花费较少的时间完成聚类，不需要逐一计算顶点间的结构相似性。这种情况随着数据量的增加，参数σ的增大显得更加明显。另外，随着数据量的增加，参数σ的增大，对相似性的计算精度要求更高[19]，那么聚类就更加困难。同时随着数据量的增加，需要更大的内存空间和计算资源，RPGC计算框架下的算法却只是在历史聚类结果中重新聚类，因此可以节约内存空间和CPU开销。

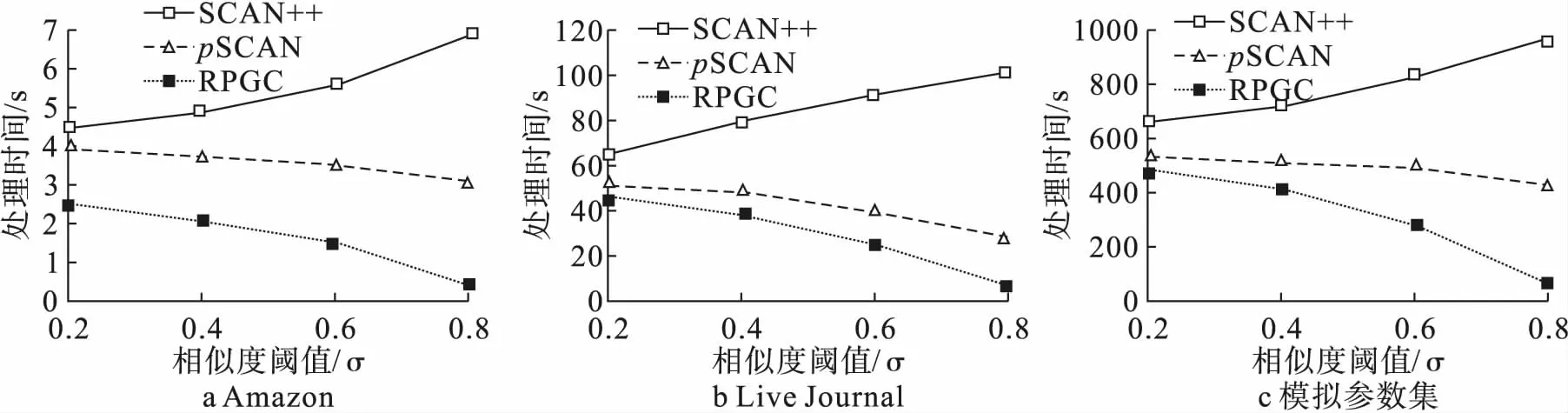
图5 不同算法在不同参数σ下的运行时间

(2)比较聚类参数μ对各算法的影响。这组实验测试图聚类参数μ对聚类时长的影响。这组实验使用3组数据集，在参数μ变化的情况下，其他参数采用默认值。实验结果如图6所示。

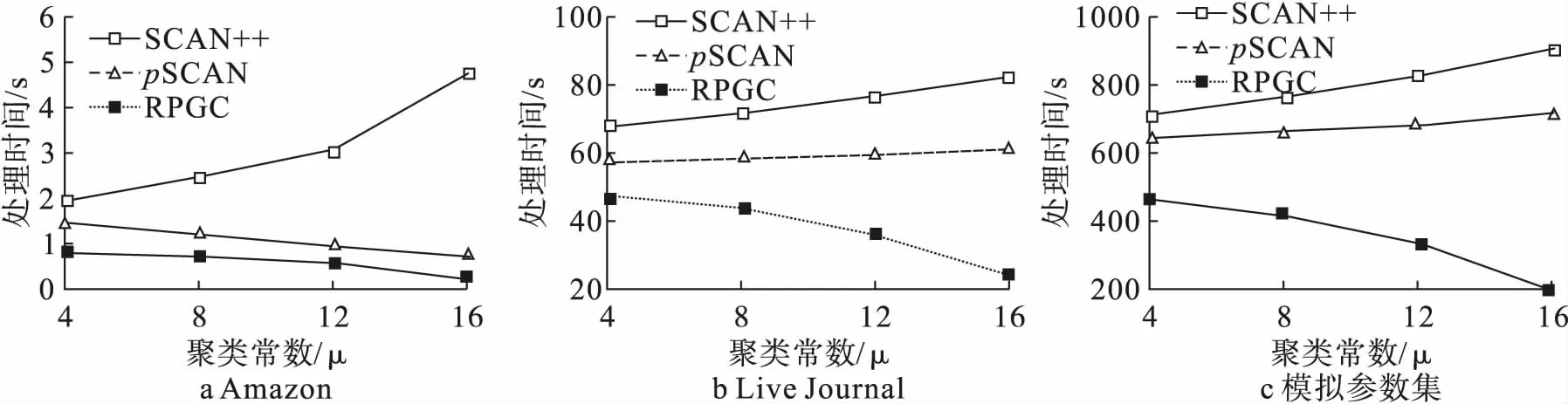
图6 不同算法在不同参数μ下的运行时间

由图6很容易看出RPGC计算框架下的算法优于其他2种算法，基于代表参数算法的运行时间仅为SCAN++算法的45%，仅为pSCAN算法运行时间的54%。但随着数据量的增加，SCAN++算法和pSCAN算法需要更长的时间，而RPGC计算框架下的算法则不同。其原因是RPGC计算框架下的算法不需要计算全部的核心顶点。而且随着参数μ的增加，被划分到同一个簇中的顶点越多，那么就需要更多的计算资源，而RPGC计算框架下的算法却不需要这些计算资源。

基于代表参数的算法始终优于现有的算法，因为RPGC计算框架下的算法不需要计算所有顶点间的结构相似性，不需要找到所有的核心顶点[20]，只是从现有的聚类结果为依据，通过计算少量顶点的相似性便可完成聚类。

4 结论

图聚类是计算机图模型中一个重要的问题。本文提出的基于代表参数的聚类方式，能够将历史聚类中所使用的参数和聚类结果进行存储并更新，使得计算代价较小，节省大量的内部存储空间。通过实验验证了该算法的优越性能。