背靠背型电力弹簧分段控制方法研究
袁敞,陈璐
背靠背型电力弹簧分段控制方法研究
袁敞,陈璐
(新能源电力系统国家重点实验室(华北电力大学), 北京 102206)
背靠背型电力弹簧作为一种负载侧调压的装置,具有无需储能元件、成本低廉的优势,然而现有的控制方法没有充分利用它的运行域。以背靠背型电力弹簧为研究对象,建立了背靠背型电力弹簧多重工作点的数学模型。将电力弹簧的运行域分为了四个部分,并根据各运行域的特点提出相应的分段控制策略。分段控制增大了背靠背型电力弹簧的运行范围,使关键负载在系统电压波动时仍然可以在额定电压下运行,保证了系统的稳定性。通过PSCAD/EMTDC的仿真,证明了所提出的分段控制可以充分利用背靠背型电力弹簧的稳态工作点。
电力弹簧;微电网;稳定运行点;调压;分段控制
0 引言
当今世界,由于化石能源带来的环境污染和能源稀缺问题,可再生能源作为一种更加清洁的能源,在能源供应中的比例不断增加。然而,由于光伏及风力等可再生能源发电都依赖于天气,这就导致了发电的波动性和不确定性。由于可再生能源在微电网中所占的发电比例较大,使得微电网的供电也具有很强的不确定性[1]。大型电网对于电压的波动有一定的自我调节能力,而小型孤立的微电网的调节能力则很弱,将导致微电网内电压和频率波动时设备不能保持原状态运行。系统电压偏高时将导致设备过电压,降低绝缘材料的使用寿命;而电压偏低将影响设备的正常工作,甚至导致设备停机[2]。频率的变化则会影响电动机的转速和设备的精确性,长时间的低频运行会损毁发电机的叶片,甚至导致系统的频率崩溃[3]。
针对电压和频率波动的问题,在源侧可以通过设置足够的旋转备用来调节电网的电压和频率[4],但是这种方法需要留有可再生能源发电裕量,损失了发电量;在网侧一般都采用调整变压器分接头的方式进行补偿[5],或是应用无功补偿装置补偿系统无功功率[6-7],然而这些装置只能调节系统电压,无法为系统频率提供支撑;储能技术可以灵活地补偿电压或是频率[8],但是储能设备成本高昂,大大提高了投资;负荷侧则可采用低频减载装置来稳定系统频率[9],然而,低频减载装置只有在系统频率降低到一定程度时才会启动,而此时负载的电能质量早已得不到保证。
这些补偿方法作用于一定区域内的所有负载,然而,系统中有的负载对电压质量要求高,如服务器、计算机、电梯和医疗设备等负载,这种负载为关键负载。而有的设备则允许电压在一定范围内波动,如空调、冷库或者是热水器等“储热/冷”负载,这种负载为非关键负载。国家发改委报道我国是全球最大的制冷产品生产、消费和出口国,制冷用电量已占到全社会用电量的15%以上[10],因此合理利用这部分负载也成为了当前一个研究热点。
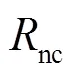
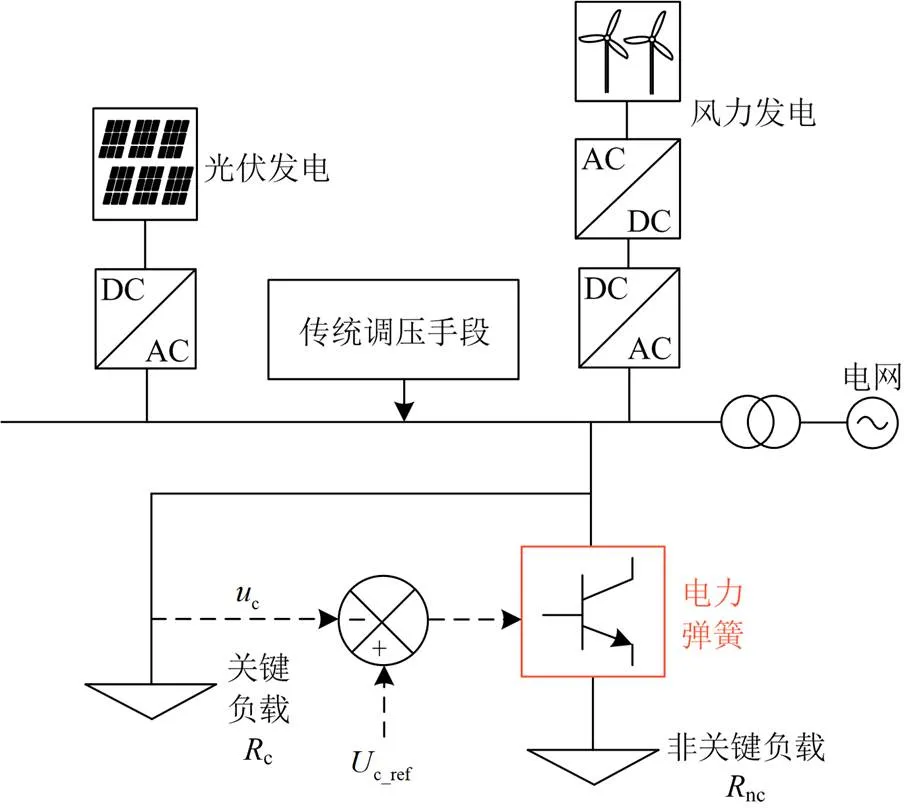
图1 微电网中电力弹簧的位置
电力弹簧可以利用非关键负载转移系统波动,具有很大的应用潜力。2015年,文献[12]提出了一种基于PR控制和电网电压前馈的电力弹簧控制方法,重点分析了电力弹簧在过电压情况下的稳压控制方法。文献[13]对电力弹簧中的各相量的相位关系进行了分析,提出了一种分析参考量与电源电压角度关系的相位控制算法,以维持电力弹簧电压稳定。同年,文献[14]对电力弹簧在有功及无功补偿方面的机理进行了详细分析,得出了电力弹簧和非关键负载共同组成的智能负载不仅具有较强的负荷响应能力,并且可以参与频率调节的结论。2017年,文献[15]对电力弹簧的稳态运行范围及越限失灵机理进行分析,通过优化关键负载的参考电压扩大电力弹簧的稳态运行范围,但是没有分析系统参数对运行范围的影响。文献[16]则指出当非关键负载值较小时电力弹簧的调压能力弱,因此提出一种控制来提高非关键负载上的电压,由此提高电力弹簧的调压能力。2019年,文献[17]结合相量图法对电力弹簧运行原理进行分析,通过无功补偿扩大其稳态运行范围,探讨了线路阻抗等参数对该范围的影响,但是所提控制方法只能调节关键负载电压,不能为系统频率稳定做出贡献。文献[18]提出了一种基于模型预测的控制策略,来调度储水式热水系统中的电力弹簧,使电力弹簧在调压的同时也参与系统调频。
然而,上述文献忽略了在系统电压不变的情况下,非关键负载可以输出不同大小的有功功率,当系统频率波动较大时,可以让电力弹簧不同工作点间来回切换来参与系统调频。文献[19]建立了非关键负载有功功率的一元二次方程,根据电力弹簧稳态工作点的状态及其运行模式,讨论了电力弹簧在各运行区域各参数之间的数学关系;2020年,文献[20]设计了能够让电力弹簧在全运行域内稳定运行并且可以在不同运行区域之间无缝切换的方法,但是该方法也只能让电力弹簧在两个有功功率点之间切换,调节系统波动范围较小。
拓扑结构决定了电力弹簧的基本运行范围,到目前为止,已经提出了不同的电力弹簧拓扑。最初提出的电力弹簧结构是将一个变流器在直流侧并联一个电容,称之为电容型电力弹簧[11]。电容型电力弹簧成本低,但是它不能提供有功功率,所以适用于只需要调节无功功率的场合。2013年,文献[21]中将电容型电力弹簧的直流侧电容换成了蓄电池,提出了电池型电力弹簧,研究了电池型电力弹簧的8种典型工作模态及其稳态分析。电池型电力弹簧可以灵活地调节有功功率和无功功率,控制较为简单,理论上适用于各种场合。但蓄电池维护和更换的成本较高,不适合大量应用于实际工业中。2016年,文献[22]将电容型电力弹簧中直流侧并联上一个变流器,形成背靠背型电力弹簧,背靠背型电力弹簧由两个变流器构成,与非关键负载直接串联的称之为串联侧电力弹簧,另一个称之为并联侧电力弹簧。背靠背型电力弹簧扩大了电容型电力弹簧的工作范围,解决了电容型电力弹簧不能补偿有功功率的缺点,抑制电压的波动效果更好。而且它从母线取电,不需要电池,成本低于电池型电力弹簧。2017年,文献[23]提出将背靠背型电力弹簧输出电压端口添加一个隔离变压器,这样可以避免因并联侧电力弹簧中性点故障而影响关键性负载电压的稳定。
为充分扩大电力弹簧的运行范围,本文采用了文献[23]中提出的电力弹簧结构,对它的稳态运行点进行研究,并分段探讨了背靠背型电力弹簧调压方法,使关键负载在额定电压下运行的同时,还能控制电力弹簧在不同稳态运行点之间切换运行,并通过仿真验证了电力弹簧在不同区域缓解电压波动的作用。
1 背靠背型电力弹簧工作原理分析
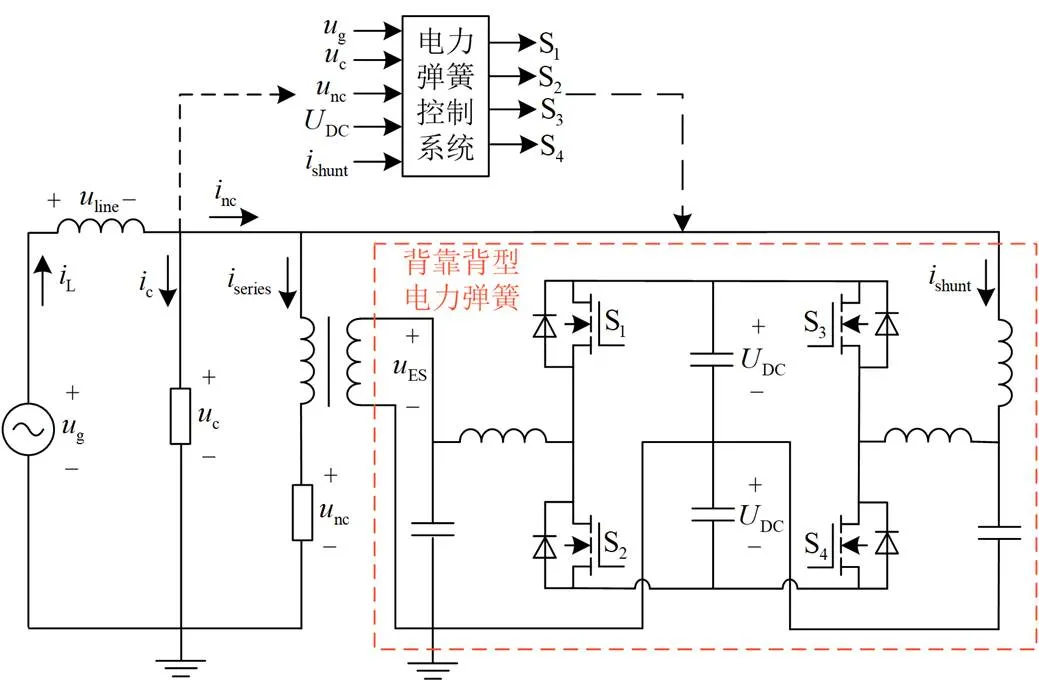
图2 背靠背型电力弹簧拓扑
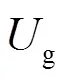

图3 背靠背型电力弹簧向量图
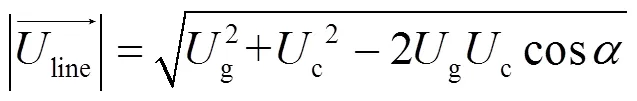
由整个系统的有功功率平衡可得
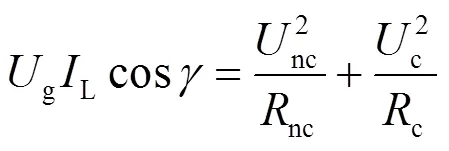
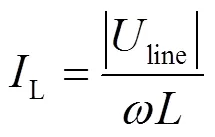
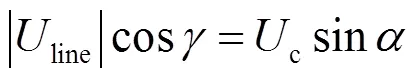
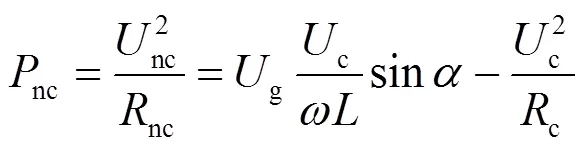
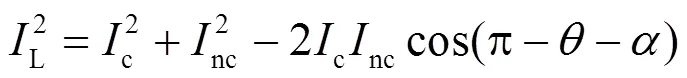
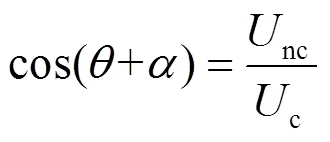
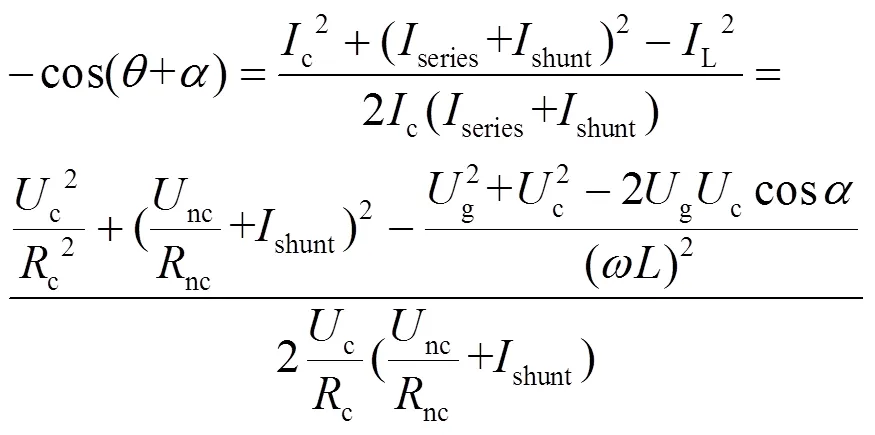
将式(5)与式(7)代入式(8),化简得
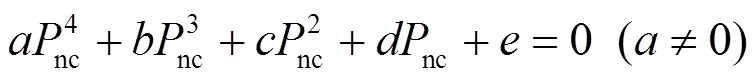
由于化简结果复杂,需要用到两次代数,其中
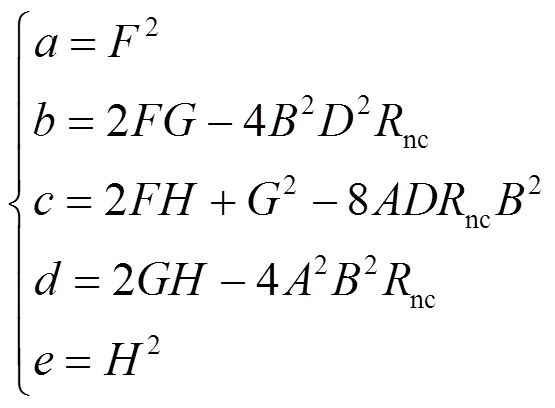
其中,
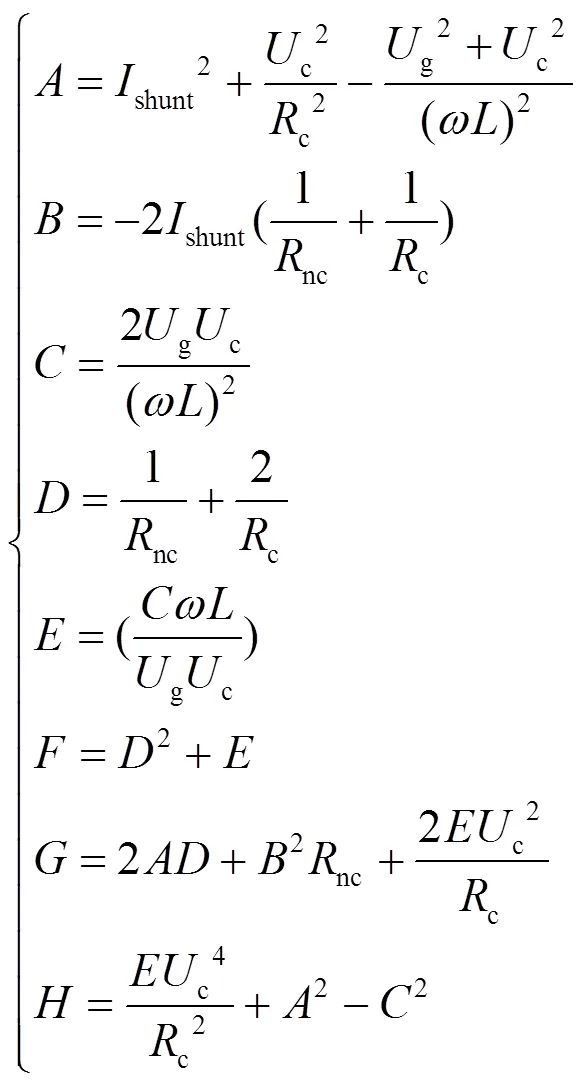
由于非关键负载为阻性负载,因此
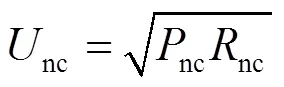
可求出电力弹簧的电压幅值为
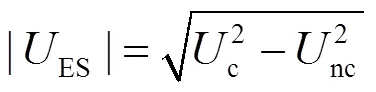
由式(5)经反三角变换得到
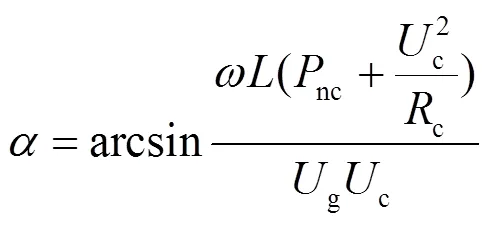
由式(7)经反三角变换得到
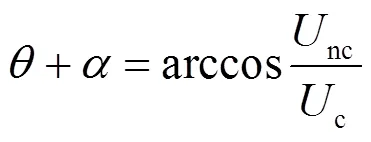
可得电力弹簧欠压模式下输出的电压相位为
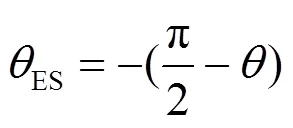
同理,根据图3(b),可得电力弹簧过压模式下平衡点的电压相位为
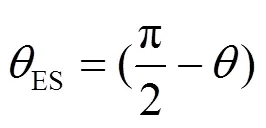
如式(9)所示,通过计算得到关于非关键负载有功功率的方程为一元四次方程。在不同的工况下,背靠背型电力弹簧的平衡点有5种可能:没有平衡点、一个平衡点、两个平衡点、三个平衡点和四个平衡点。在工况确定后,可以由式(13)得到电力弹簧输出电压幅值,由式(16)或式(17)得到电力弹簧输出电压相位。
2 ES-B2B的运行区域以及相应的控制
根据非关键负载有功功率一元四次方程的4个解,再加上电力弹簧根据系统电压的偏差存在的欠压和过压工作模式,实际运行中的背靠背型电力弹簧存在着8种运行状态。为了确保背靠背型电力弹簧在稳定状态下进行电压调节,同时利用非关键负载消耗有功的多少使电力弹簧参与系统调频,有必要对背靠背型电力弹簧的运行区域进行分析,并划分其对应的工作区域。
为了尽可能地扩大电力弹簧的工作区域,本文选定在背靠背型电力弹簧存在四个工作点的工作区域,分别在电源电压高于220 V与低于220 V额定值的情况下进行电压控制。根据式(9)得到非关键负载有功功率一元四次方程的4个根。以表1中的系统参数为实例,对非关键负载有功功率方程进行进一步说明。
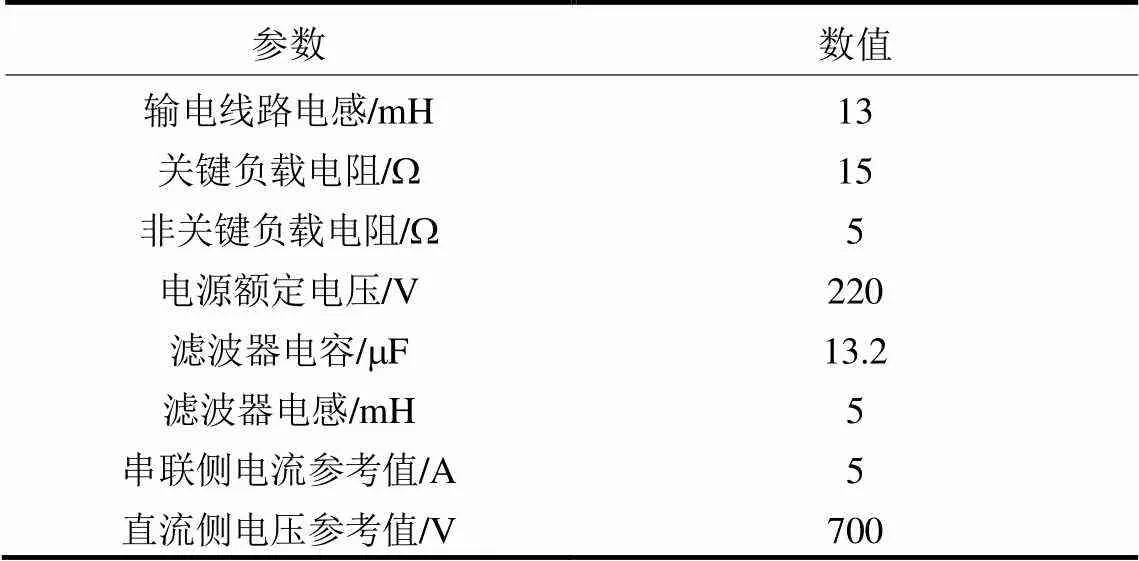
表1 背靠背型电力弹簧系统参数
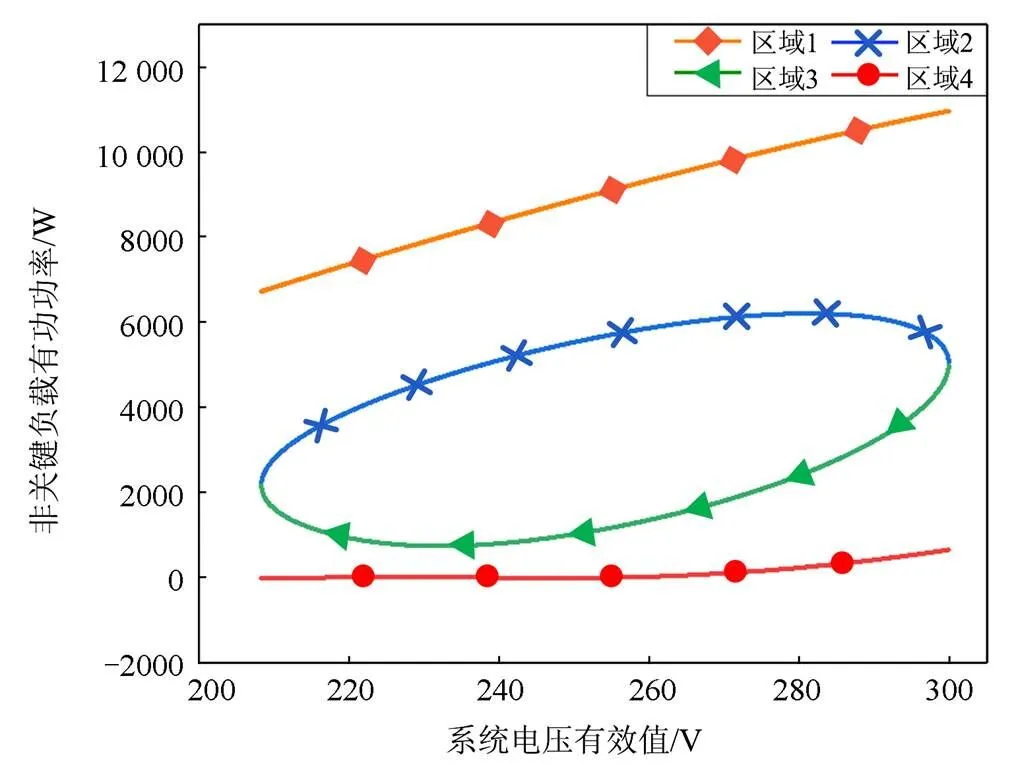
图4 四区域内系统电压有效值与非关键负载有功功率关系
从图4可知,在同一工况下运行时,运行于平衡点4时非关键负载消耗的有功功率远低于运行于平衡点1时非关键负载消耗的有功功率。因此,当系统频率波动较大时,可以充分利用背靠背型电力弹簧的工作区域,控制电力弹簧在这四个工作点切换运行,从而深度参与系统频率调节。
由此划分出四个区域:非关键负载有功功率在平衡点1时对应区域1;非关键负载有功功率在平衡点2时对应区域2;非关键负载有功功率在平衡点3时对应区域3;非关键负载有功功率在平衡点4时对应区域4。以电力弹簧工作在欠压模式为例,不同区域的单调性如图5所示。
图5(a)为系统电压有效值与背靠背型电力弹簧输出电压有效值的关系。当电力弹簧工作在区域1和区域2时,随着系统电压的升高,电力弹簧输出电压随之降低;当背靠背型电力弹簧工作在区域3和区域4时,随着系统电压的升高,电力弹簧输出电压随之升高。
图5(c)是将图5(b)中各区域进行放大得到的,从图5(b)和图5(c)都能看到背靠背型电力弹簧输出电压相角与输出电压有效值的关系,当电力弹簧分别工作在4个区域时,电力弹簧输出电压相角与输出电压有效值始终呈正比关系。同理可以得出如图6所示的背靠背型电力弹簧工作在过压模式的单调性。
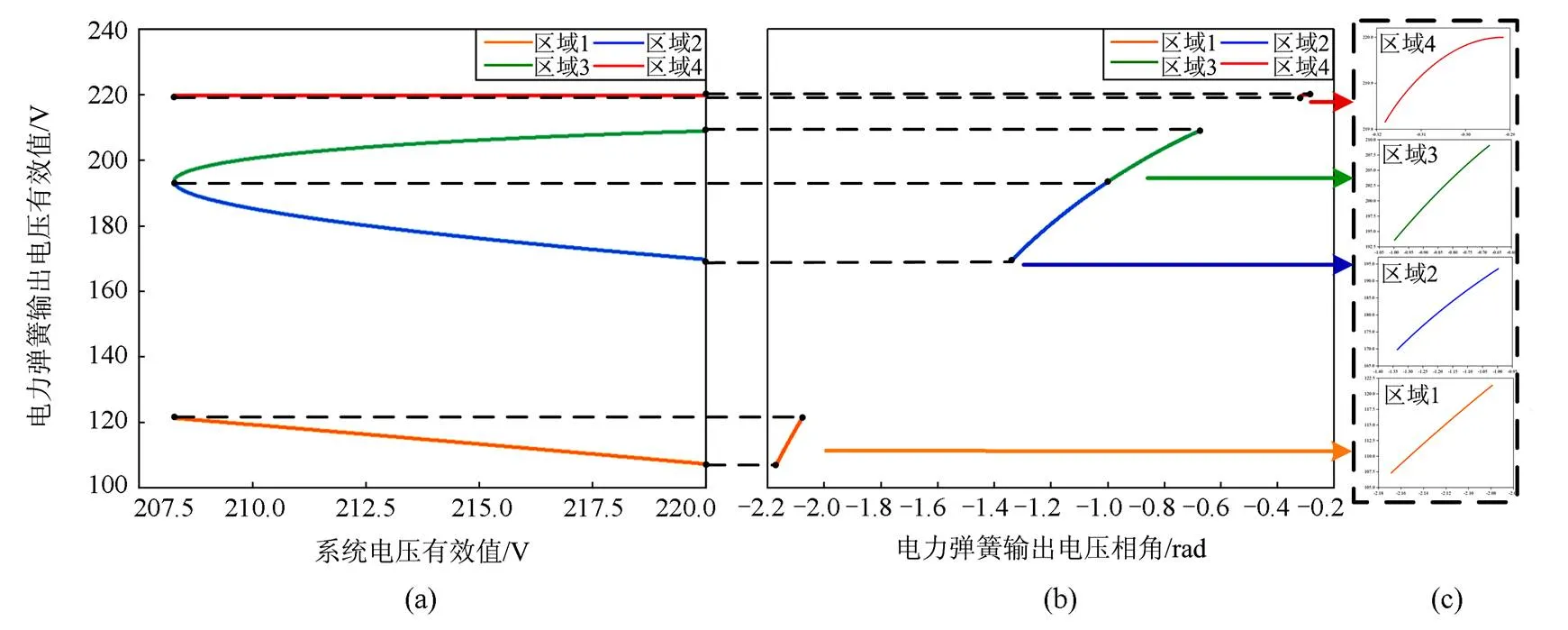
图5 欠压模式下四区域内背靠背型电力弹簧单调性
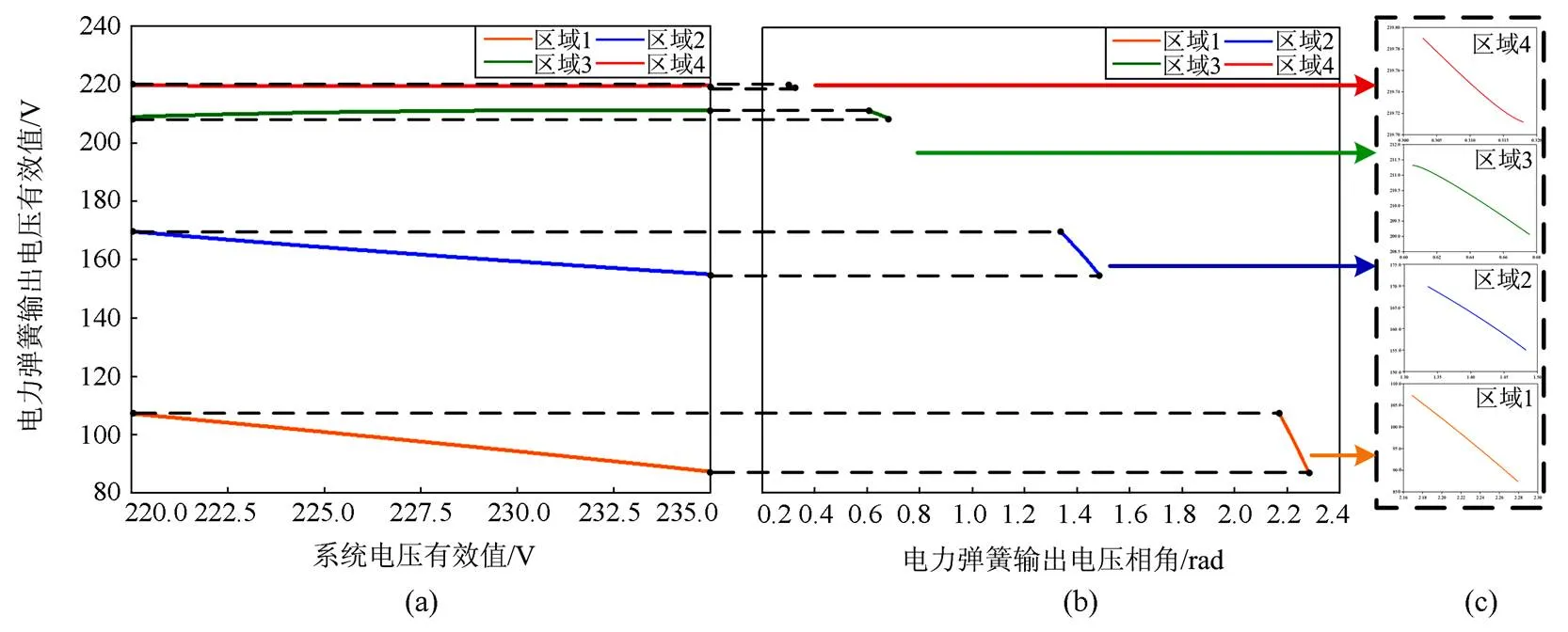
图6 过压模式下四区域内背靠背型电力弹簧单调性
根据各区域的单调性设计出如图7所示的分段控制方法,由式(9)功率方程模块得到对应的一元四次方程,根据频率的波动程度选择电力弹簧工作的区域,再根据系统电压的情况选择工作于欠压模式还是过压模式,通过相角计算模块由式(16)或式(17)得出电力弹簧输出电压的相角,从而实现背靠背型电力弹簧在不同区域的切换。
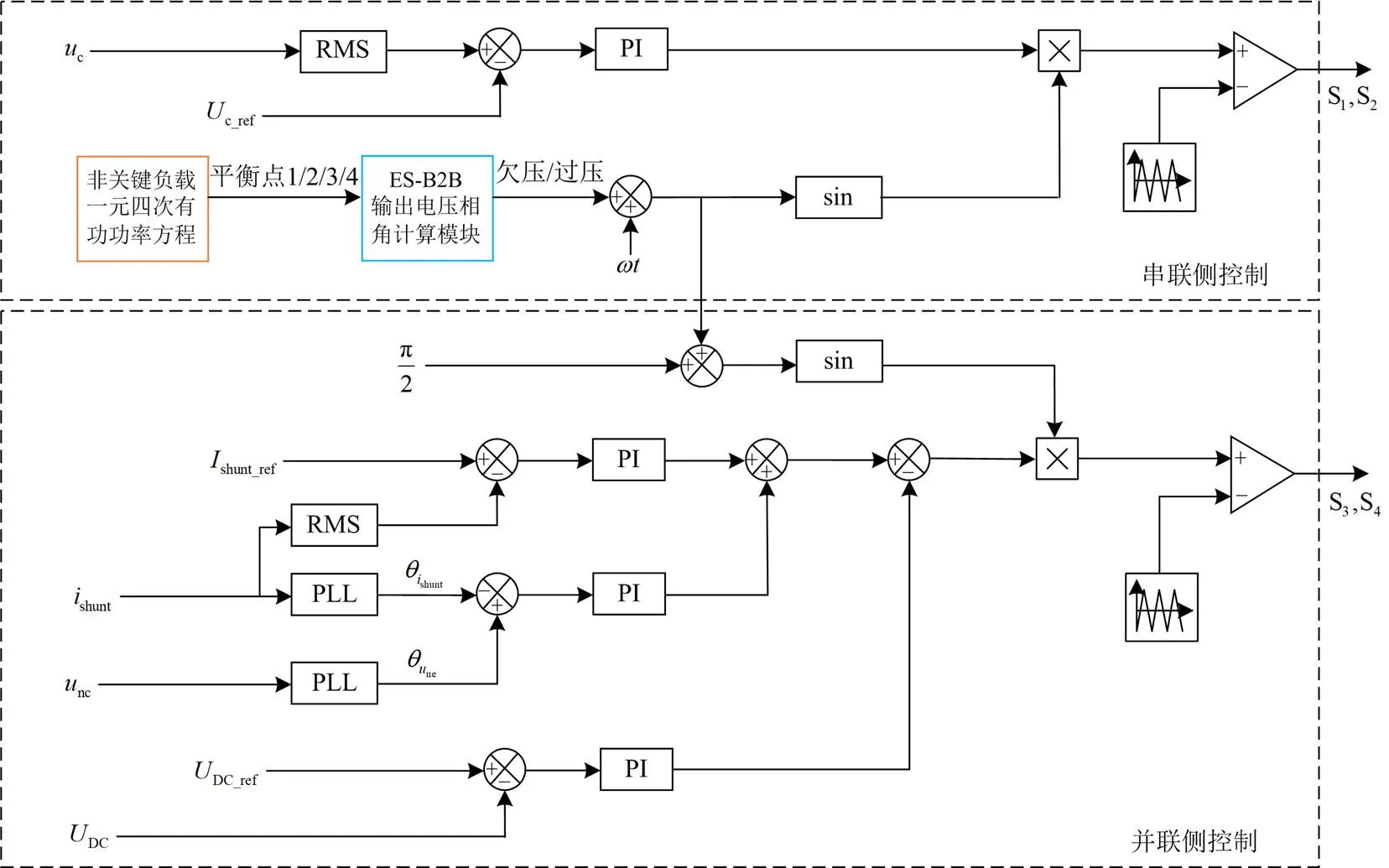
图7 背靠背型电力弹簧分段控制框图
3 仿真验证
在实际应用中,系统频率会发生波动,所以为了调节系统频率,需要控制背靠背型电力弹簧在不同的平衡点切换,通过非关键负载消耗不同大小的有功功率来参与调频,所以接下来本文将验证背靠背型电力弹簧在各平衡点间的切换。在验证过程中,仅以一个方向为例,例如在验证了从平衡点1至平衡点2后,不再赘述从平衡点2至平衡点1的过程。
3.1 电力弹簧工作于欠压模式
使系统电压工作于215 V的欠压模式,在背靠背型电力弹簧多重工作点控制方法下,仿真结果如下所述。
3.1.1区域1切换至区域2
在绝大多数情况下,应该使背靠背型电力弹簧工作于消耗有功功率最小的区域4,然而当系统频率波动较大且频率偏高时,为了消耗更多有功功率,从而降低系统频率,应当控制电力弹簧工作在对应非关键负载有功功率最高的区域1。
当电力弹簧工作在区域1时,如果系统频率轻微下降,可以控制电力弹簧切换至区域2,以减小非关键负载上的电压降落,从而减少消耗的有功功率。所以使电力弹簧工作在区域1,1 s时,控制电力弹簧从区域1切换至区域2,该工况下的仿真结果见图8—图10所示。
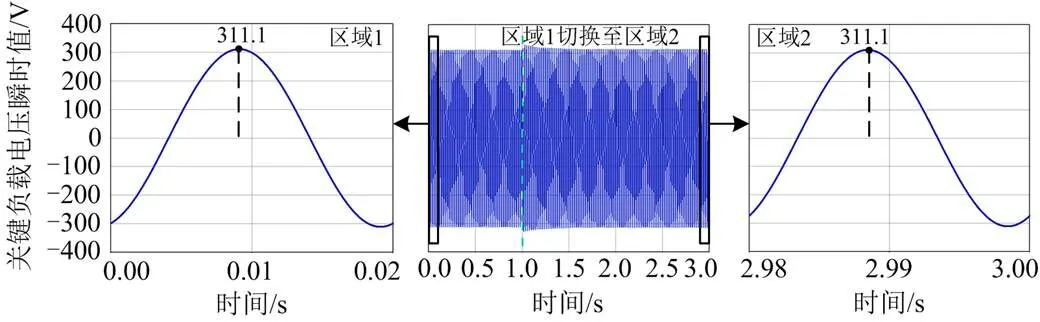
图8 关键负载电压瞬时值
如图8所示,通过仿真结果可以看出,在欠电压模式下,当电力弹簧工作在区域1时,关键负载电压幅值为311.1 V,对应有效值为220 V的额定电压。切换至区域2后,关键负载电压经控制后还能稳定在220 V。说明当系统欠压时,该控制方法在区域切换前后都可以将关键负载电压稳定在额定值。
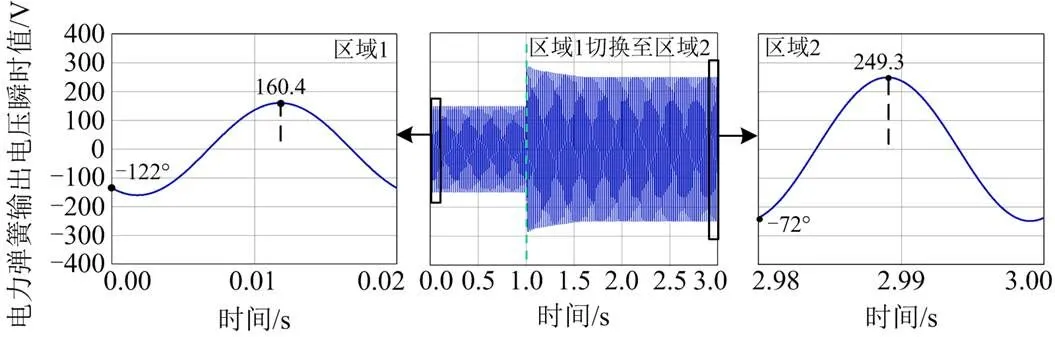
图9 电力弹簧输出电压瞬时值
由图9可知,切换前电力弹簧工作在区域1,电力弹簧输出电压幅值为160.4 V,输出电压相角为-122°;切换后电力弹簧工作在区域2,电力弹簧输出电压幅值为249.3 V,输出电压相角为-72°。
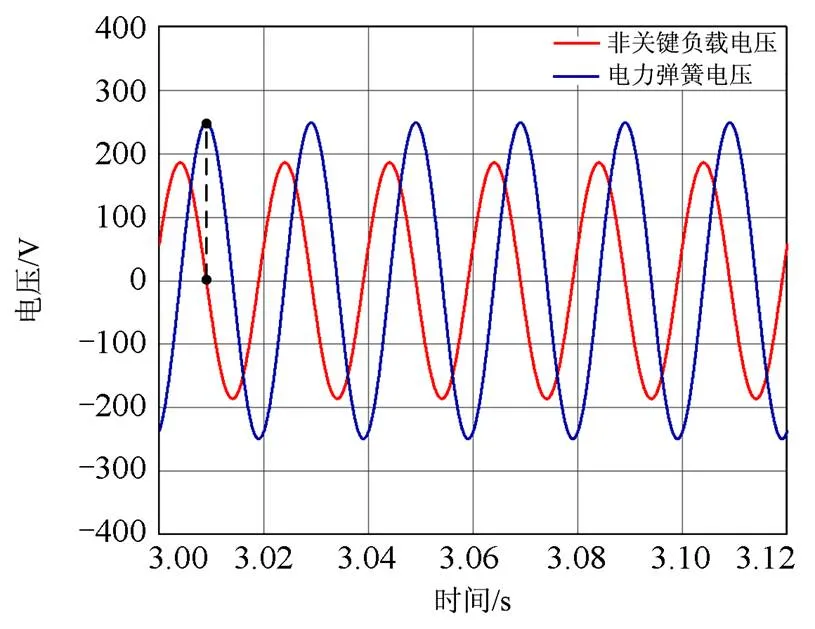
图10 非关键负载电压与电力弹簧电压关系
由于电力弹簧在确定了工作区域后,如果系统参数不发生变化,工作点也不会发生变化,所以本文只讨论切换后电力弹簧稳定运行时系统电压与电力弹簧的电压关系。如图10所示,3 s后,电力弹簧稳定运行在区域2,输出电压幅值为249.3 V,相角为-72°,非关键负载电压幅值为186.2 V,相角为17°,与第2节所计算的结果相吻合。此时非关键负载消耗的有功功率较大,有利于降低系统频率,电力弹簧的相角滞后非关键负载电压90°,证明了电力弹簧在起升压作用时呈现与电容相似的特性,赋予电力弹簧物理意义。
3.1.2区域2切换至区域3
当系统频率在额定值附近时,为了提高电力弹簧的灵活性,应当控制电力弹簧工作于区域2,以便在非关键负载消耗有功功率大于或小于区域2的区域来回切换,从而使电力弹簧深度参与系统调频。
所以使电力弹簧工作在区域2,1 s时,控制电力弹簧从区域2切换至区域3,该工况下的仿真结果见图11—图13所示。
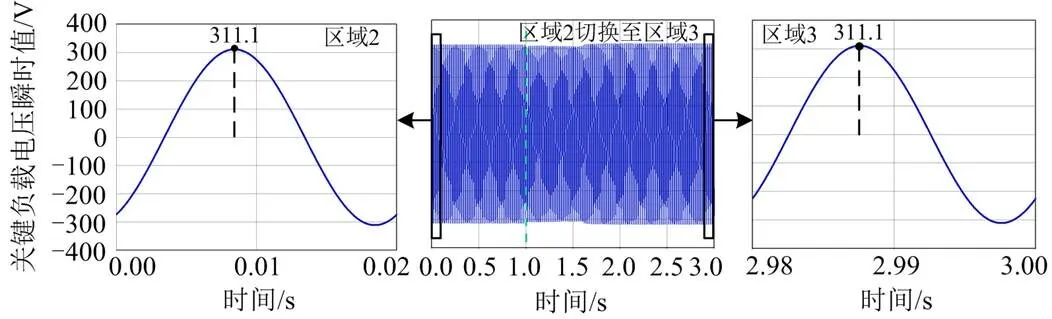
图11 关键负载电压瞬时值
如图11所示,在欠电压模式下,当电力弹簧工作在区域2时,关键负载电压为220 V的额定电压。切换至区域3后,关键负载电压经控制后还能稳定在220 V。说明当系统欠压时,该控制方法在区域切换前后都可以使关键负载工作在额定电压。

图12 电力弹簧输出电压瞬时值
由图12可知,切换前电力弹簧工作在区域2,电力弹簧输出电压幅值为249.3 V,输出电压相角为-72°;切换后电力弹簧工作在区域3,电力弹簧输出电压幅值为291.7 V,输出电压相角为-43°。
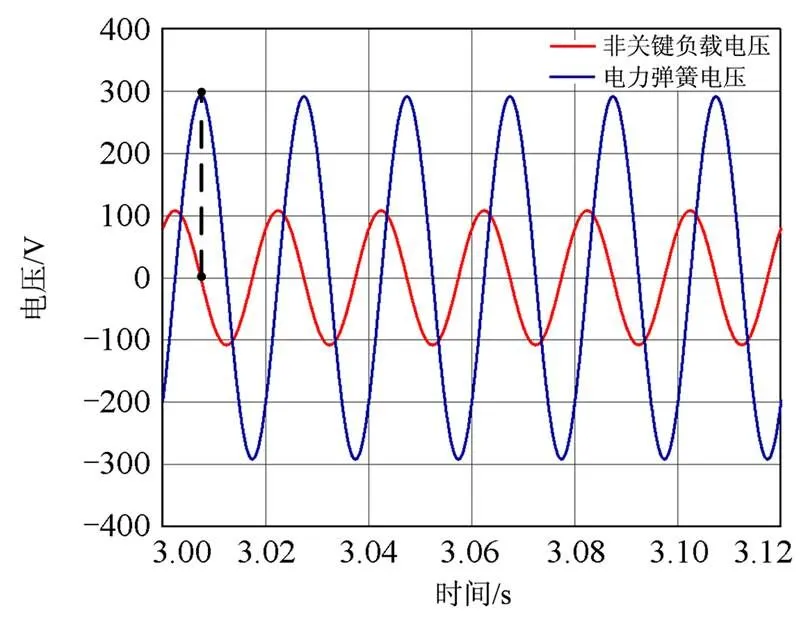
图13 非关键负载电压与电力弹簧电压关系
由图13可知,3 s后,电力弹簧工作于区域3,输出电压幅值为291.7 V,相角为-43°,非关键负载电压幅值为108.1 V,相角为47°,与第2节中所计算的结果相吻合。此时非关键负载消耗的有功功率较小,有利于提高系统频率,电力弹簧相角滞后非关键负载90°,证明了电力弹簧在起升压作用时呈现与电容相似的特性,赋予电力弹簧物理意义。
3.1.3区域3切换至区域4
当系统频率略低于额定值,需要非关键负载消耗更少的有功功率时,应当控制电力弹簧工作在对应非关键负载有功功率为平衡点3的区域3,并通过仿真验证电力弹簧由区域3切换至另一个区域的工作情况。
使电力弹簧工作在区域3,1 s时,控制电力弹簧从区域3切换至区域4,该工况下的仿真结果如图14—图16所示。
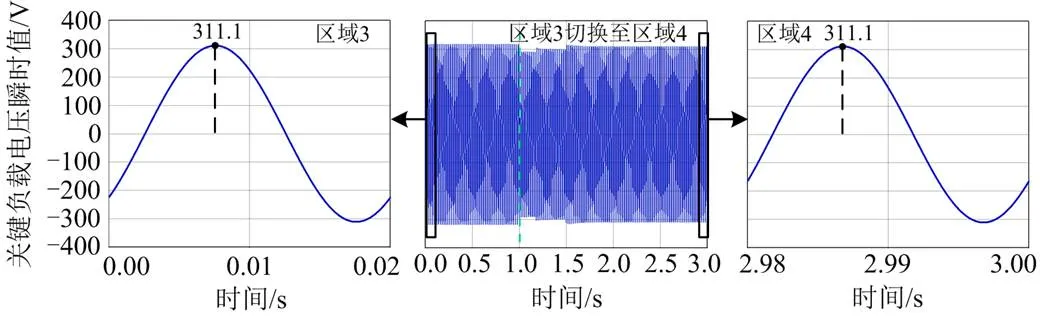
图14 关键负载电压瞬时值
如图14所示,在欠电压模式下,当电力弹簧工作在区域3时,关键负载电压有效值为220 V。切换至区域4后,经控制后关键负载还能稳定工作在额定电压下。充分验证了在区域切换后该控制方法的稳压特性。
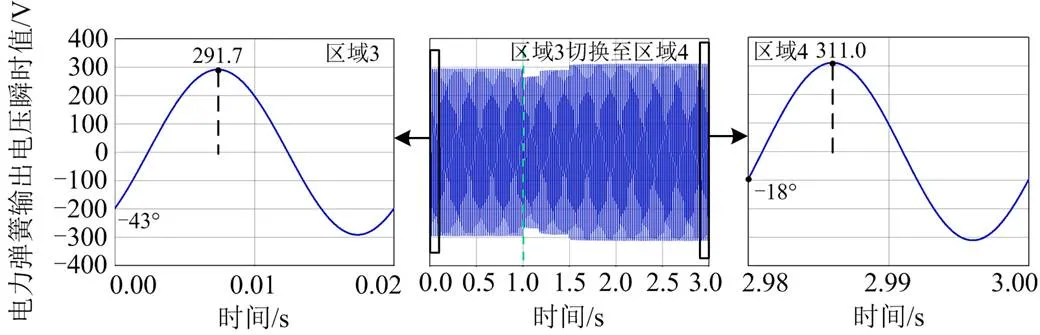
图15 电力弹簧输出电压瞬时值
由图15可知,切换前电力弹簧工作在区域3,电力弹簧输出电压幅值为291.7 V,输出电压相角为-43°;切换后电力弹簧工作在区域4,电力弹簧输出电压幅值为311.0 V,输出电压相角为-18°。
由图16可知,3 s后,电力弹簧运行于区域4,输出电压幅值为311.0 V,相角为-18°,非关键负载电压幅值为8.1 V,相角为72°,与第2节中所计算的结果相吻合。非关键负载几乎不消耗有功功率,有利于提高系统频率,电力弹簧的相角滞后非关键负载电压90°,证明了电力弹簧在起升压作用时呈现与电容相似的特性,赋予电力弹簧物理意义。
3.1.4区域4切换至区域1
当系统频率下降显著,需要非关键负载几乎不消耗有功功率时,应当控制电力弹簧工作在对应非关键负载有功功率最小的区域4,这样可以使电力弹簧在起调压作用时还能为系统频率稳定做出贡献,并验证电力弹簧于区域4 的切换情况。
使电力弹簧工作在区域4,1 s时,控制电力弹簧从区域4切换至区域1,该工况下的仿真结果如图17—图19所示。
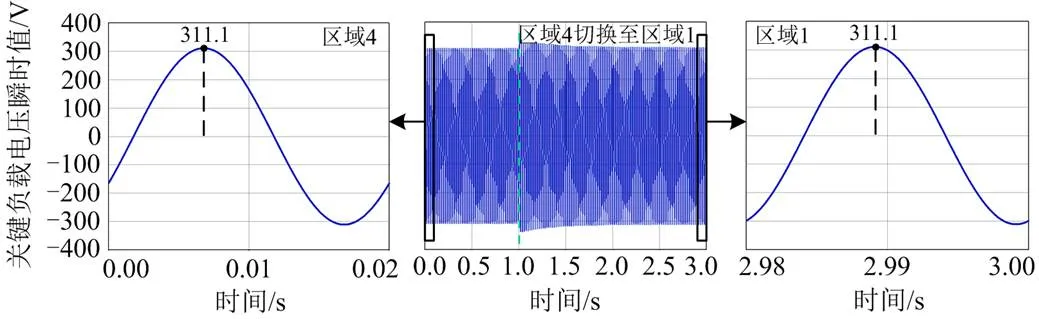
图17 关键负载电压瞬时值
如图17所示,在欠电压模式下,当电力弹簧工作在区域4时,关键负载电压有效值为220 V。切换至区域1后,经控制后关键负载还能稳定工作于220 V。验证了在切换前后该控制方法都可以起到调节关键负载电压的作用。
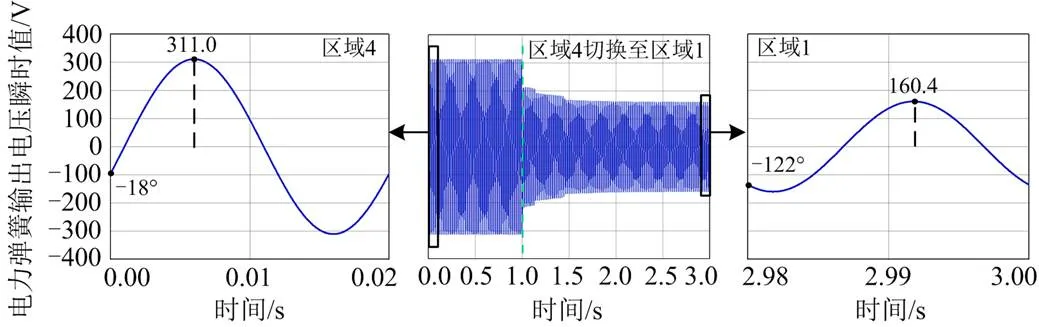
图18 电力弹簧输出电压瞬时值
由图18可知,切换前电力弹簧工作在区域4,电力弹簧输出电压幅值为311.0 V,输出电压相角为-18°;切换后电力弹簧工作在区域1,电力弹簧输出电压幅值为160.4 V,输出电压相角为-122°。

图19 非关键负载电压与电力弹簧电压关系
由图19可知,3 s后,电力弹簧稳定运行于区域1,输出电压幅值为160.4 V,相角为-122°,非关键负载电压幅值为266 V,相角为-32°,与第2节中所计算的结果相吻合。此时非关键负载消耗的有功功率最大,有利于降低系统频率,电力弹簧的相角滞后非关键负载电压90°,证明了电力弹簧在起升压作用时呈现与电容相似的特性,赋予电力弹簧物理意义。
3.2 电力弹簧工作于过压模式
使系统电压工作于225 V的过压模式,在背靠背型电力弹簧多重工作点控制方法下,仿真结果如下所述。
3.2.1区域1切换至区域2
使电力弹簧工作在区域1,1 s时,控制电力弹簧从区域1切换至区域2,该工况下的仿真结果如图20—图22所示。
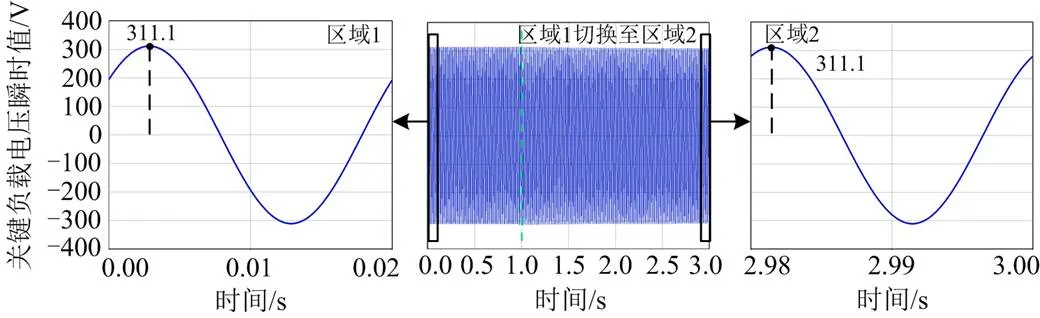
图20 关键负载电压瞬时值
如图20所示,在欠电压模式下,当电力弹簧工作在区域1时,关键负载电压幅值为311.1 V,对应有效值为220 V的额定电压。切换至区域2后,关键负载电压经控制后能稳定在220 V额定电压。说明当系统欠压时,该控制方法在区域切换前后都可以将关键负载电压稳定在额定值。
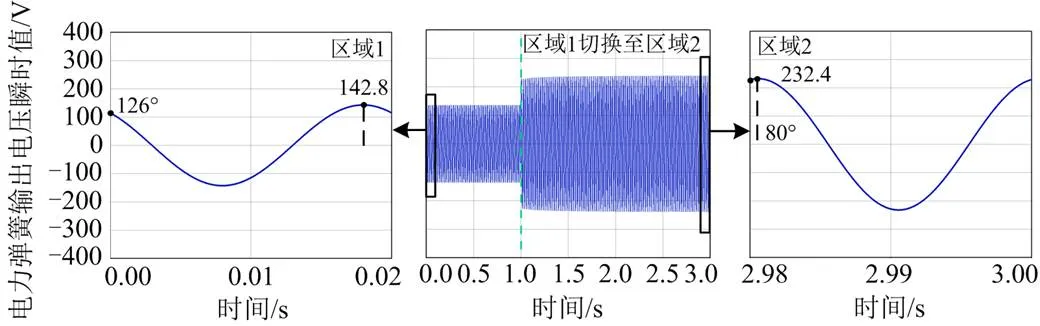
图21 电力弹簧输出电压瞬时值
由图21可知,切换前电力弹簧工作在区域1,电力弹簧输出电压幅值为142.8 V,输出电压相角为126º;切换后电力弹簧工作在区域2,电力弹簧输出电压幅值为232.4 V,输出电压相角为80º。
图22所示的是切换到区域2平稳运行后系统电压与电力弹簧电压瞬时值的关系。3 s后,电力弹簧稳定输出电压幅值为232.4 V,相角为80º,非关键负载电压幅值为206.8 V,相角为-10º,与所计算的结果相吻合。此时非关键负载消耗的有功功率较大,有利于降低系统频率,电力弹簧的相角超前于非关键负载电压90º,证明了电力弹簧在起降压作用时呈现与电感相似的特性,赋予电力弹簧物理意义。
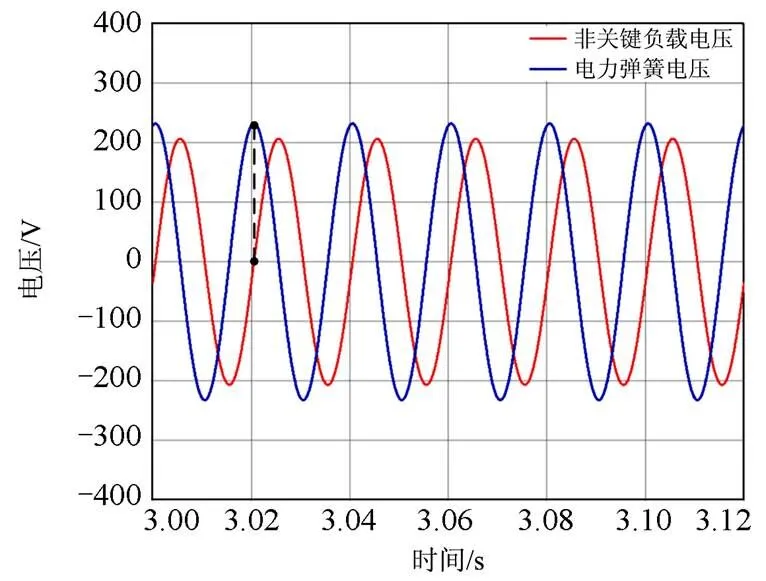
图22 非关键负载电压与电力弹簧电压关系
3.2.2区域2切换至区域3
使电力弹簧工作在区域2,1 s时,控制电力弹簧从区域2切换至区域3,该工况下的仿真结果见图23—图25所示。
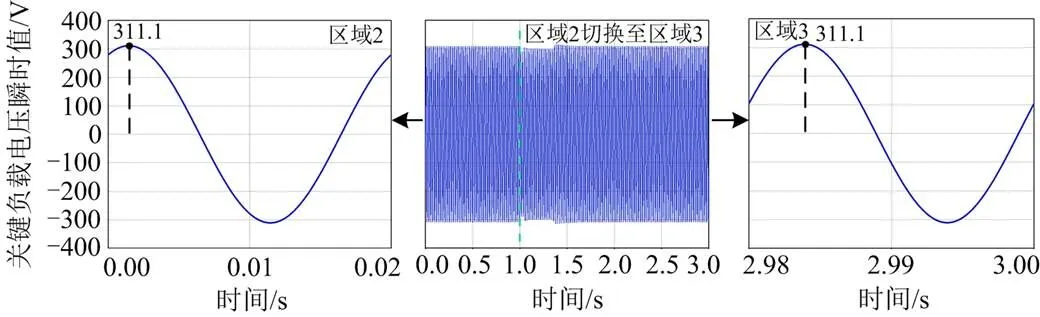
图23 关键负载电压瞬时值
如图23所示,在感性电压模式下,当电力弹簧工作在区域2时,关键负载电压为220 V的额定电压。切换至区域3后,关键负载电压经控制后还能稳定在220 V。说明当系统过压时,该控制方法在区域切换前后都可以使关键负载工作在额定电压。
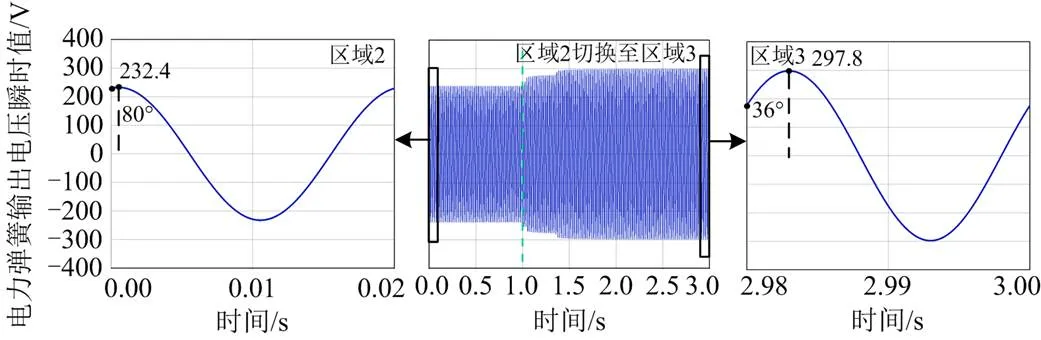
图24 电力弹簧输出电压瞬时值
由图24可知,切换前电力弹簧工作在区域2,电力弹簧输出电压幅值为232.4 V,输出电压相角为80º;切换后电力弹簧工作在区域3,电力弹簧输出电压幅值为297.8 V,输出电压相角为36º。
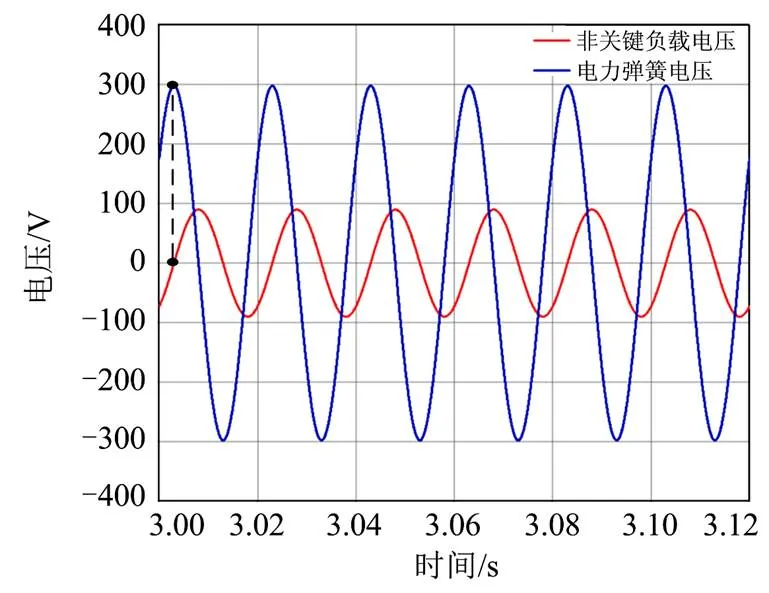
图25 非关键负载电压与电力弹簧电压关系
由图25可知,3 s后,电力弹簧工作在区域3,输出电压幅值为297.8 V,相角为36º,非关键负载电压幅值为89.9 V,相角为-53º。此时非关键负载消耗的有功功率较小,有利于提高系统频率,电力弹簧的相角超前于非关键负载电压90º,证明了电力弹簧在起降压作用时呈现与电容相似的特性,赋予电力弹簧物理意义。
3.2.3区域3切换至区域4
使电力弹簧工作在区域3,1 s时,控制电力弹簧从区域3切换至区域4,该工况下的仿真结果如图26—图28所示。
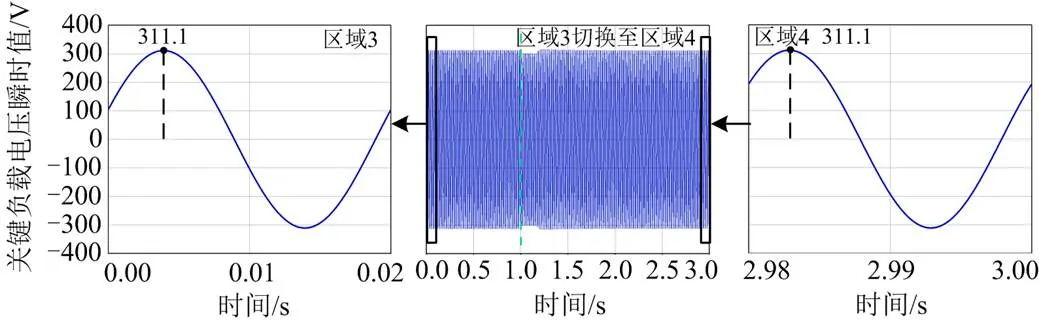
图26 关键负载电压瞬时值
如图26所示,在感性模式下,当电力弹簧工作在区域3时,关键负载电压有效值为220 V。切换至区域4后,经控制后关键负载还能稳定工作在额定电压下。充分验证了在区域切换前后该控制方法的稳压效果。
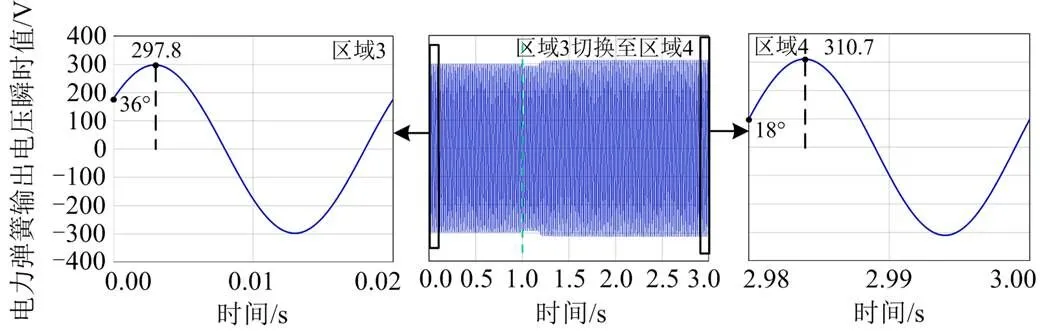
图27 电力弹簧输出电压瞬时值
由图27可知,切换前电力弹簧工作在区域3,电力弹簧输出电压幅值为297.8 V,输出电压相角为36º;切换后电力弹簧工作在区域4,电力弹簧输出电压幅值为310.7 V,输出电压相角为18º。
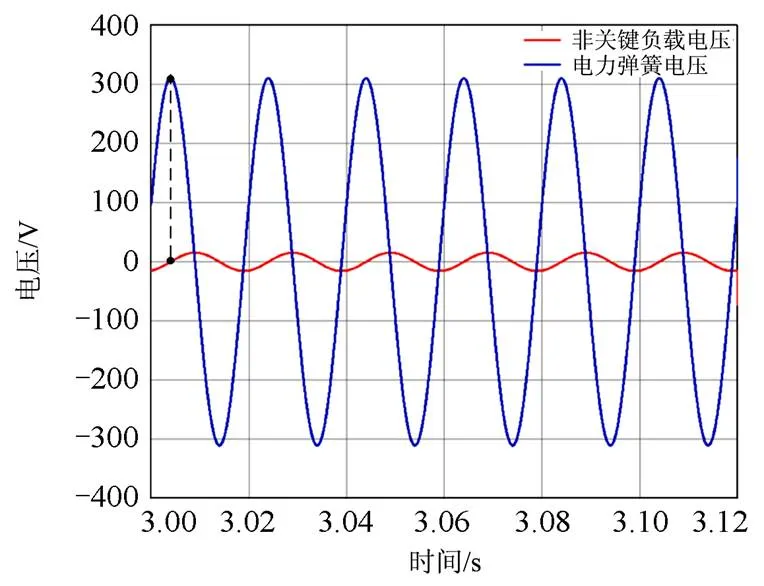
图28 非关键负载电压与电力弹簧电压关系
由图28可知,3 s后,电力弹簧运行于区域4,输出电压幅值为310.7 V,相角为18º,非关键负载电压幅值为15.5 V,相角为-71º,与第2节中所计算的结果相吻合。非关键负载几乎不消耗有功功率,有利于提高系统频率,电力弹簧的相角超前于非关键负载电压90º,证明了电力弹簧在起降压作用时呈现与电感相似的特性,赋予电力弹簧物理意义。
3.2.4区域4切换至区域1
当系统频率下降显著,需要非关键负载几乎不消耗有功功率时,应当控制电力弹簧工作在对应非关键负载有功功率最小的区域4,这样可以使电力弹簧在起调压作用时还能为系统频率稳定做出贡献,并验证电力弹簧在区域4 的切换情况。
使电力弹簧工作在区域4,1 s时,控制电力弹簧从区域4切换至区域1,该工况下的仿真结果如图29—图31所示。
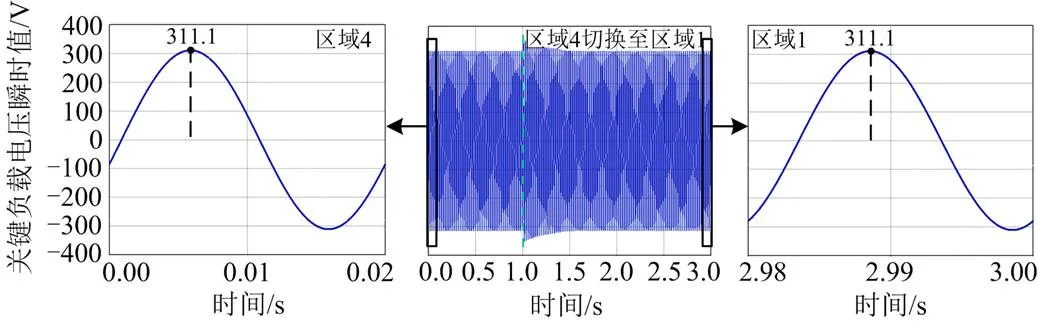
图29 关键负载电压瞬时值
如图29所示,欠压模式下电力弹簧工作在区域4时,关键负载电压有效值为220 V。切换至区域1后,经控制后关键负载还能稳定工作于220 V。验证了在切换前后该控制方法都可以起到调节关键负载电压的作用。
由图30可知,切换前电力弹簧工作在区域4,电力弹簧输出电压幅值为310.7 V,输出电压相角为18°;切换后电力弹簧工作在区域1,电力弹簧输出电压幅值为142.8 V,输出电压相角为126°。
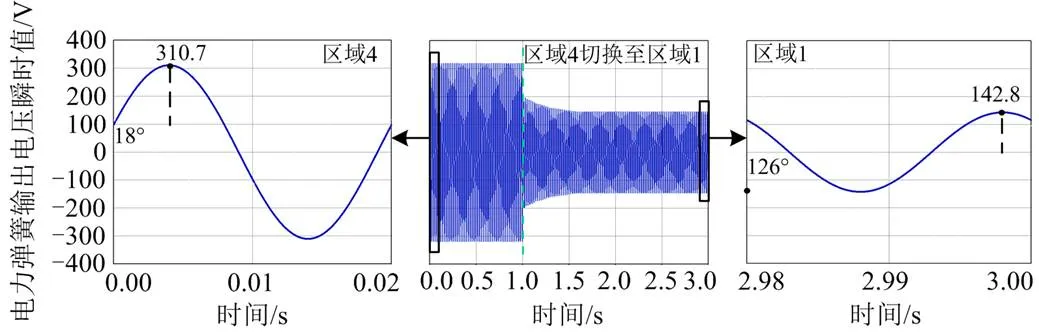
图30 电力弹簧输出电压瞬时值
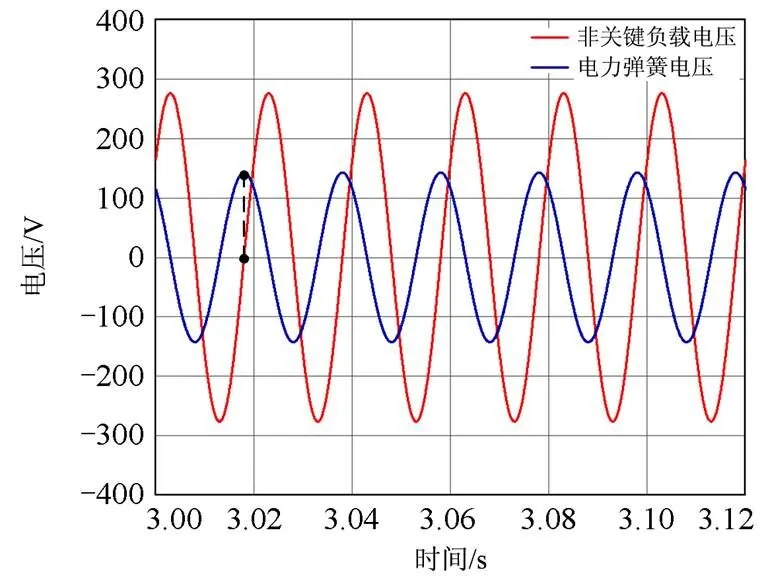
图31 非关键负载电压与电力弹簧电压关系
由图31可知,3 s后,电力弹簧稳定运行于区域1,输出电压幅值为142.8 V,相角为126°,非关键负载电压幅值为276.4 V,相角为36°,与第2节中所计算的结果相吻合。此时非关键负载消耗的有功功率最大,有利于降低系统频率,电力弹簧的相角超前非关键负载电压90°,证明了电力弹簧在起降压作用时呈现与电感相似的特性,赋予电力弹簧物理意义。
4 结论
本文以经济性高、控制复杂的背靠背型电力弹簧为研究对象,提出了一种电力弹簧多重工作点运行的控制方法,得到以下结论:
1) 分析了背靠背型电力弹簧的工作机理。在系统欠压的情况下,电力弹簧起到了与电容相似的作用,从而提升关键负载电压;在系统过压的情况下,电力弹簧呈现与电感相似的特性,从而降低关键负载电压。并作出了容性模式与感性模式下背靠背型电力弹簧的向量图,建立其数学模型,并推导得出关于背靠背型电力弹簧非关键负载有功功率的一元四次方程。
2) 通过对背靠背型电力弹簧各稳态工作点的分析,得到了电力弹簧的运行特性。在区域1,非关键负载消耗有功功率最多,电力弹簧输出电压负载最小;在区域2,非关键负载消耗有功功率较多,电力弹簧输出电压负载较小;在区域3,非关键负载消耗有功功率较少,电力弹簧输出电压负载较大;在区域4,非关键负载消耗有功功率最少,电力弹簧输出电压负载最大。
3) 基于各工作区域的单调性分析,提出了一种新的控制策略。所提控制策略可以使电力弹簧在不同稳态工作点保证关键负载运行在额定电压,解决了大规模可再生能源并入电网所带来的电压波动问题。
4) 基于PSCAD/EMTDC的详细仿真验证了该控制方法的有效性。
[1] 赵东元, 胡楠, 傅靖, 等. 提升新能源电力系统灵活性的中国实践及发展路径研究[J]. 电力系统保护与控制, 2020, 48(24): 1-8.
ZHAO Dongyuan, HU Nan, FU Jing, et al. Research on the practice and road map of enhancing the flexibility of a new generation power system in China[J]. Power System Protection and Control, 2020, 48(24): 1-8.
[2] 谢峥, 杨楠, 刘钊, 等. 考虑不确定性和安全效能成本的配电网低电压综合治理方法[J]. 电力系统保护与控制, 2020, 48(9): 36-48.
XIE Zheng, YANG Nan, LIU Zhao, et al. Low voltage comprehensive management method of a distribution network considering the uncertainty and safety efficiency cost[J]. Power System Protection and Control, 2020, 48(9): 36-48.
[3] 李军徽, 冯喜超, 严干贵, 等. 高风电渗透率下的电力系统调频研究综述[J]. 电力系统保护与控制, 2018, 46(2): 163-170.
LI Junhui, FENG Xichao, YAN Gangui, et al. Survey on frequency regulation technology in high wind penetration power system[J]. Power System Protection and Control, 2018, 46(2): 163-170.
[4] 陈海鹏, 周越豪, 王趁录, 等. 基于改进的CNN- LSTM短期风功率预测的系统旋转备用经济性分析[J]. 高电压技术, 2022, 48(2): 439-448.
CHEN Haipeng, ZHOU Yuehao, WANG Chenlu, et al. Economic analysis of system spinning reserve based on improved CNN-LSTM short term wind power prediction[J]. High Voltage Engineering, 2022, 48(2): 439-448.
[5] 彭志炜, 胡国根, 韩祯祥.有载调压变压器调整对电力系统电压稳定性的影响[J]. 中国电机工程学报, 1998, 18(6): 33-37, 67.
PENG Zhiwei, HU Guogen, HAN Zhenxiang. The power system voltage stability affected by on-load tap changer[J]. Proceedings of the CSEE, 1998, 18(6): 33-37, 67.
[6] 郑海涛, 郑昕, 吴兴全, 等. 大型并网风电场和光伏电站内动态无功补偿的应用技术分析[J]. 电力系统保护与控制, 2014, 42(16): 149-154.
ZHENG Haitao, ZHENG Xin, WU Xingquan, et al. Technical analysis of dynamic reactive power compensation equipment applied in large-scale grid connected wind power plant and photovoltaic substation[J]. Power System Protection and Control, 2014, 42(16): 149-154.
[7] 李旷, 刘进军, 魏标, 等. 静止无功发生器补偿电网电压不平衡的控制及其优化方法[J]. 中国电机工程学报, 2006, 26(5): 58-63.
LI Kuang, LIU Jinjun, WEI Biao, et al. Control and optimization of static var generator for grid voltage unbalance mitigation[J]. Proceedings of the CSEE, 2006, 26(5): 58-63.
[8] 孙立明, 杨博. 蓄电池/超导混合储能系统非线性鲁棒分数阶控制[J]. 电力系统保护与控制, 2020, 48(22): 76-83.
SUN Liming, YANG Bo. Nonlinear robust fractional-order control of battery/SMES hybrid energy storage systems[J]. Power System Protection and Control, 2020, 48(22): 76-83.
[9] 盛四清, 赵文天, 樊茂森. 适应新能源高占比系统的低频减载优化方法[J]. 太阳能学报, 2022, 43(2): 157-162.
SHENG Siqing, ZHAO Wentian, FAN Maosen. Optimization method of UFLS for high proportion of new energy proportion system[J]. Acta Energiae Solaris Sinica, 2022, 43(2): 157-162.
[10] 中华人民共和国国家发展和改革委员会. 绿色高效制冷行动方案[DB/OL]. http://www.gov.cn/xinwen/2019- 06/19/content_5401443.htm, 2019.
National Development and Reform Commission. Green and efficient refrigeration action plan[DB/OL]. http:// www.gov.cn/xinwen/2019-06/19/content_5401443.htm, 2019.
[11] HUI S Y, LEE C K, WU F F. Electric springs—a new smart grid technology[J]. IEEE Transactions on Smart Grid, 2012, 3(3): 1552-1561.
[12] 程明, 王青松, 张建忠. 电力弹簧理论分析与控制器设计[J]. 中国电机工程学报, 2015, 35(10): 2436-2444.
CHENG Ming, WANG Qingsong, ZHANG Jianzhong. Theoretical analysis and controller design of electric springs[J]. Proceedings of the CSEE, 2015, 35(10): 2436-2444.
[13] WANG Qingsong, CHENG Ming, CHEN Zhe, et al. Steady-state analysis of electric springs with a novel δ control[J]. IEEE Transactions on Power Electronics, 2015, 30(12): 7159-7169.
[14] AKHTAR Z, CHAUDHURI B, HUI S Y. Primary frequency control contribution from smart loads using reactive compensation[J]. IEEE Transactions on Smart Grid, 2015, 6(5): 2356-2365.
[15] 程益生, 陆振纲, 汪可友, 等. 电力弹簧稳态运行范围及越限失灵机理分析[J]. 电力系统自动化, 2017. 41(14): 147-152.
CHENG Yisheng, LU Zhengang, WANG Keyou, et al. analysis on steady-state operating range and off-limits malfunction mechanism of electrical spring[J]. Automation of Electric Power Systems, 2017, 41(14): 147-152.
[16] KEYKHAH E, BARAKATI S M, TAVAKOLI S. Overcoming limitation of electric spring[C] // Power Electronics, Drive Systems & Technologies Conference, February 14-16, 2017, Mashhad, Iran: 437-441.
[17] 尹发根, 王淳. 基于无功补偿的电力弹簧有效运行范围分析[J]. 电力系统保护与控制, 2019, 47(15): 9-16.
YIN Fagen, WANG Chun. Analysis of the effective operating range of electric spring based on reactive power compensation[J]. Power System Protection and Control, 2019, 47(15): 9-16.
[18] LIANG L, HOU Y, HILL D J. Enhancing flexibility of an islanded microgrid with electric springs[J]. IEEE Transactions on Smart Grid, 2019, 10(1): 899-909.
[19] YUAN Chang, FENG Jiayao, TONG Ming, et al. Piecewise control strategy for electric spring[J]. IET Generation, Transmission & Distribution, 2019, 13(12): 2496-2506.
[20] YUAN Chang, FENG Jiayao, QIU Junqing, et al. Seamless mode-switching control for electric spring with capacitor DC bank[J]. IET Generation, Transmission & Distribution, 2020, 14(21): 4824-4834.
[21] TAN S, LEE C K, HUI S Y. General steady-state analysis and control principle of electric springs with active and reactive power compensations[J]. IEEE Transactions on Power Electronics, 2013, 28(8): 3958-3969.
[22] AKHTAR Z, CHAUDHURI B, SHU Y. Smart loads for voltage control in distribution networks[C] // 2016 IEEE Power and Energy Society General Meeting (PESGM), July 17-21, 2016, Boston, MA, USA.
[23] HUI S Y, LEE C, YANG T, et al. Extending the operating range of electric spring using back-to-back converter: hardware implementation and control[J]. IEEE Transactions on Power Electronics, 2017, 32(7): 5171-5179.
A piecewise control strategy for a back-to-back electric spring
YUAN Chang, CHEN Lu
(State Key Laboratory of Alternate Electrical Power System with Renewable Energy Sources (North China Electric Power University), Beijing 102206, China)
As a load-side voltage regulating device, the back-to-back electric spring has the advantages of no energy storage element and low cost. However, the existing control methods don’t make full use of its operating domain. This paper takes the back-to-back electric spring as the research object and establishes the mathematical model of multiple working points of the spring. The operating domain of the spring is divided into four parts, and a corresponding segmented control strategy is proposed according to the characteristics of each operating domain. Piecewise control increases the running range of the spring, so that the critical load can still run at the rated voltage when the system voltage fluctuates, and the system can run stably. The simulation results of PSCAD/EMTDC also prove that the proposed piecewise control can make full use of the steady-state operating point of the back-to-back electric spring.
electric spring; microgrid; stable running point; voltage regulation; piecewise control
10.19783/j.cnki.pspc.210954
国家自然科学基金项目资助(51877081)
This work is supported by the National Natural Science Foundation of China (No. 51877081).
2021-07-22;
2021-12-01
袁 敞(1981—),男,通信作者,博士,副教授,硕士生导师,研究方向为电能质量分析与控制,电力电子技术在电力系统中的应用等;E-mail: yc_ncepu@163.com
陈 璐(1997—),女,硕士研究生,研究方向为电力电子技术在电力系统中的应用等。E-mail: chenluer123456@ 163.com
(编辑 魏小丽)
——以某大厦地下停车场第二层开挖管道工程为例*

