考虑非关键线路影响的PERT网络计划完工概率分析
丁 雨 琦
(桂林理工大学土建学院,广西 桂林 541004)
随着工程建设的不断发展,项目规模愈加增大、影响因素愈加复杂,工程项目的计划与控制变得愈加重要。进度管理一直是工程项目管理重难点,由于工程项目受影响因素繁多,完工是一个不确定的事件,一般以(给)完工概率来表示项目能在指定时间内完成的可能性。研究工程项目的完工概率对工程项目的计划与控制、项目资源的分配与节约有着重大意义。复杂工程项目中均存在因经验不足、不确定因素过多导致活动持续时间不确定的问题。现代的项目管理中广泛应用计划评审技术PERT(Program/Project Evaluation and Review Technique)进行工程项目的计划与控制。PERT由美国学者Malcolm等[1]于1950年提出,美国海军运用计划评审制度成功缩短了2年“北极星”导弹计划的制造时间,最终在世界上得到广泛的推广与应用。但运用经典PERT法计算工程项目的完工概率时,通行的做法是以网络计划图中关键路线的完工概率作为项目的完工概率,不考虑非关键线路。而实际上,非关键路线的方差较大时非关键线路的完工概率有可能小于关键线路的完工概率,此时项目的完工概率可能会由非关键线路决定。因此,分析PERT网络计划中非关键路线与关键路线的完工概率,讨论何种情况下非关键线路会主导工程项目完工概率的,是一个值得研究的问题。
1 基本概念和计算方法

(1)
(2)
网络计划中每一个工序的持续时间Tij计算完成后,用期望值
代表工序持续时间,可将不确定性网络计划转变为确定性网络计划,因此可用关键路径法寻找关键路径及关键工作。关键线路上各个工作的持续时间之和即为项目工期的期望值,由中心极限定理可知,项目工期近似服从正态分布,其均值与方差即为关键路线上各工序工期持续时间期望值之和、方差之和。因此项目的工期持续时间期望值和方差为:
TE=∑Tij
(3)
(4)
项目在给定的要求工期T0下的完工概率可按下式计算:
(5)

(6)
根据λ值,在标准正态分布表[4]上查得的数值即为要求工期为T0时工程项目的完工概率。
2 典例分析
某施工项目的各项工作持续时间估计值如表1所示,项目进度计划网络图见图1,各个工序的持续时间见表1。
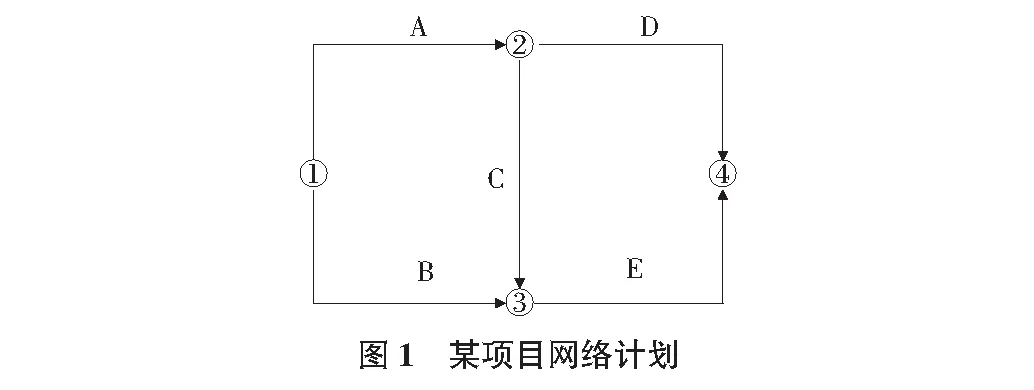

表1 各项活动持续时间估计值 d
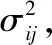

表2 各工作期望时间和方差汇总表
图1中网络图有三条线路,可分别计算每条线路的完工时间期望值分别为:22 d(线路A-C-E)、20.83 d(线路A-D)、16.16 d(线路B-E),其中最长线路A-C-E为关键线路,其线路完工时间的期望值为22 d,方差为2.072。如要求项目在25 d内完工,此时完工概率为:
查标准正态分布表可得:
P(λ≤1.45)=92.65%。
即该项目在25 d内完工的概率为92.65%。
以上分析过程即为PERT计算项目完工概率的一般做法,直接用关键线路分析完工概率,放弃分析非关键线路。这种做法是否妥当,可结合算例来具体分析。算例中非关键线路有两条,计算两条线路完工时间的方差,并结合其完工时间的期望值进行分析,见表3。两条非关键线路在25 d内的完工概率分别为83.54%(线路A-D)、99.99%(线路B-E)。而前已算得关键线路A-C-E的完工概率为92.65%,显然整个项目能在25 d内完工的可能性不是关键线路的92.65%,而是非关键线路的83.54%,即算例项目的完工概率是由非关键线路确定的。因此利用PERT进行项目完工概率计算时,不考虑非关键线路的影响是不完善的。关键线路的完工概率不一定决定项目的完工概率,计算时需考虑非关键线路对完工概率的影响。

表3 非关键线路工期、方差和完工概率
是不是每个项目的完工概率计算都要考虑非关键线路的影响,答案显然是不一定的,以下继续讨论什么情况下需要考虑非关键线路,什么情况下可不考虑非关键线路,直接用关键线路分析即可。
3 非关键线路决定完工概率的条件
由以上算例可知,非关键线路有可能会决定项目的完工概率,只考虑关键线路的做法是不完善的,有必要讨论何种情况下必须考虑非关键线路,以便得到科学准确的项目完工概率。继续对算例进行深入分析,考虑不同要求工期T0下的完工概率,设关键线路的工期期望值为TE,对以下情形进行具体分析。
1)T0=TE时。
算例中,即T0=TE=22 d,可计算各线路的完工概率如表4所示。
此时施工项目的完工概率由关键线路A-C-E决定。
2)T0 例如要求工期T0=21 d时,项目完工概率,分析了当要求工期T0为21 d时,各线路的完工概率如表5所示。 表4 各线路工期、方差和完工概率(T0=TE=22 d) 表5 各线路工期、方差和完工概率(T0=21 d) 此时施工项目在21 d内完工的概率由关键线路A-C-E决定。可以继续分析,取T0=20 d,19 d,…,1 d,分析结果都是一样的结论,关键线路决定此项目的完工概率。 3)T0>TE时。 当要求工期T0为23 d时,各线路的完工概率见表6。 表6 各线路工期、方差和完工概率(T0=23 d) 此时施工项目的完工概率依然由关键线路A-C-E决定,但非关键线路A-E的完工概率逐渐趋近于关键线路A-C-E的完工概率。 要求工期T0为24 d时,各线路的完工概率如表7所示。 此时施工项目的完工概率不再由关键线路A-C-E决定,而是由非关键线路A-D决定。继续增大要求工期T0,得到的结论也是一致的,都是非关键线路决定项目完工概率。这是由于非关键线路的方差较大,工期的概率分布较为分散所致。 综上,该施工项目运用PERT方法计算项目完工概率时,若要求工期不小于24 d时,非关键线路决定项目的完工概率,单独分析关键线路会得到错误的结果,必须考虑非关键线路对项目完工概率的影响。 通过以上分析可知,在PERT网络计划中,要求工期T0不大于关键线路的工期持续时间期望值TE时,关键线路的完工概率小于任意非关键线路的完工概率,此时直接分析关键线路即可得到项目的完工概率;要求工期大于关键线路的工期期望值TE时,且非关键线路方差明显大于关键线路的方差时,必须考虑非关键线路对工程项目完工概率的影响,对关键线路与非关键线路都进行按时完工的可能性分析,以便得到正确结论,更好的指导工程项目管理。


4 结语

