基于改进缩方差法的工期固定-资源均衡优化方法
高 婷
重庆交通大学,重庆 400074
0 引言
在网络计划中,最大资源需求量小于或等于实际可供应的资源,就是一个可行的网络计划。在建设工程施工中,当工期固定时,为减少资源浪费、降低成本,对资源配置进行优化以提高企业经济效益。对于工期固定的资源均衡配置问题,常用的方法有很多,例如缩方差法(方差法)[1]、方差值最小法[2]、削峰填谷法[3]等。缩方差法在资源均衡配置中应用较广。对于大型工程项目来说,网络计划的工序很多,若用原始的方法步骤求解,就会使有限时间内的优化工作变得不可行。因此,引入非关键工序组[4]的概念,将多个非关键工作放在一组进行调整,以减少调整步骤。原有方差法是对问题进行逐一试算、逐一调整,不能一次达到最大限度的资源均衡,特别是在大型网络计划中,使得计算和调整尤为繁琐,降低优化效率。因此,引入最小方差法的概念,选择使方差变化最大的移动时间作为调整时间。 本文结合非关键工序组概念与最小方差法对原有缩方差法进行改进,并给出非关键工序组调整判别式的一般化形式,进一步简化了计算过程。
1 缩方差法
方差是衡量随机变量或一组数据时离散程度的度量,概率论中方差用来度量随机变量和其数学期望之间的偏离程度。网络计划中,把每项工作上所配备的资源看作随机变量,利用时差来调整工作的开始时间和与完成时间以缩小方差,当这组随机变量方差值尽可能小的时候,即资源得到尽可能均衡的分配。
缩方差法是利用平衡性指标作为网络计划实现资源优化的定量指标,以Δ作为判定是否进行资源调整的依据。当Δ≤0时,可以对非关键工作进行调整,调整后变小,说明资源得到更均衡的分配。
1.1 平衡性指标∑R2
资源消耗的均方差可用下式表示[5]。
(1)
(2)
1.2 调整判别式Δ

(3)
Δ′=Rj+1-Ri+Rmn
(4)
式中:若Δ<0,则∑R2减少,该工作可以进行调整;若Δ=0,则∑R2无变化,该工作可以不调整也可以调整;若Δ>0,则∑R2增加,该工作不能进行调整。同理,当该工作推迟nd时,资源变化量判别式如下[1]。
(5)
式中:k为累计推迟时间,R(j+n)为该非关键工作在第j+n天的资源需求量,R(i+n-1)为该非关键工作在第i+n-1天的资源需求量,tmn为该非关键工作的持续时间,T1为总推迟时间。
2 非关键工序组
非关键工序组定义为初始总时差相等的非关键工序的集合。按工序总时差的大小,将非关键工序分组,同一组内的工序,总时差相等,将单一非关键工序(即没有与此工序总时差相同的工序)看成是只有一个工序的非关键工序组。将非关键工序组视为网络图中的1个独立单位来进行资源均衡优化。非关键工序组优化判别式由姚玉玲 等[4]提出,由实例分析得判别公式。
ΔFGJ=REF+1-RES+1+R1≤0
(6)
式中:ES和EF分别为非关键工序组的最早开始时间和最早完成时间,R1为非关键工序组中第1个工作的资源需要量。此公式为非关键工序组移动1个单位时间的判别公式,将公式一般化得到非关键工序组移动n个单位时间的判别式。
Δ′=
(7)
式中:T1为推迟的总时间;n为推迟的单位时间;kmn为非关键工序mn推迟的累计时间;tmn为非关键工序mn持续时间;kmn-tmn为非关键工序mn被推迟天数与持续时间之差;Rmn为非关键工序mn上的资源需求量;REF+n为第EF+n天的资源需求量,RES+n为第ES+n天的资源需求量;∑(kmn-tmn)Rmn为该非关键工序组中每个kmn≤tmn的非关键工序的推迟时间和持续时间之差与其资源需求量之积的和。
3 最小方差法

(8)
(9)
4 资源优化步骤

5 实例应用
图1为双代号时标网络图及某种资源需要量动态数列。假定时间单位为d。

图1 初始时标网络图及资源需求量
5.1 原始方法资源优化过程
5.1.1 第1次调整
在网络图中,利用时差进行调整的顺序是自右向左逆箭线方向进行。当同一时间有多个工序拥有自由时差时,按单位时间资源需要量由大到小的顺序进行调整。因此在图1中,先考虑工序5→7的移动。
计算Δ′,计算式参考式(4)、(5)。
①R(10+1)-R(3+1)+R57=2-10+4=-4<0,可右移1 d。
②R(10+2)-R(3+2)+R57=2-9+4=-3<0,可右移1 d,共2 d。
③R(10+3)-R(3+3)+R57=2-9+4=-3<0,可右移1 d,共3 d。
④R(10+4)-R(3+4)+R57=2-8+4=-2<0,可右移1 d,共4 d。
⑤R(10+5)-R(3+5)+R57=2-8+4=-2<0,可右移1 d,共5 d。
由于自由时差已全部用完,且所有Δ′均小于等于0,所以5→7工序一共可以移动5 d。
5.1.2 第2次调整
由于工序2→7自由时差存在最后,所以考虑工序2→7的移动。
计算Δ′,计算式参考式(4)、(5)。
①R(9+1)-R(6+1)+R27=-2+3=1>0,不可移动1 d。
考察工序2→7是否可以移动2 d,3 d,…,6 d。

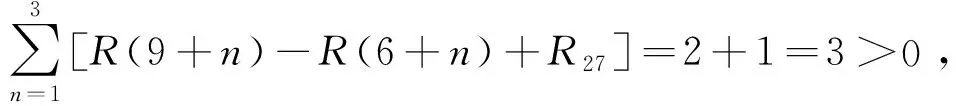
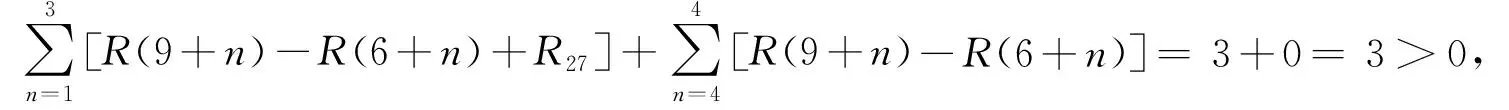


由上述计算知,工序2→7不可向右移动,所以以下考虑工序3→5的调整。
计算Δ′,计算式参考式(4)、(5)。
①R(3+1)-R(2+1)+R35=6-8+2=0,可向右移动1 d。
②R(3+2)-R(2+2)=5-6=-1<0,可向右移动1 d,共2 d。
③R(3+3)-R(2+3)=5-5=0,可向右移动1 d,共3 d。
④R(3+4)-R(2+4)=4-5=-1,可向右移动1 d,共4 d。
⑤R(3+5)-R(2+5)=4-4=0,可向右移动1 d,共5 d。
由上述式子可知,工序3→5可向右移动5 d,资源得到更均衡的分配,现对1→3工作进行调整。
5.1.3 第3次调整
计算Δ′,计算式参考式(4)、(5)。
①R(2+1)-R(0+1)+R13=6-7+1=0,可向右移动1 d。
②R(2+2)-R(0+2)+R13=6-7+1=0,可向右移动1 d,共2 d。
③R(2+3)-R(0+3)=5-6=-1<0,可向右移动1 d,共3 d。
④R(2+4)-R(0+4)=5-6=-1<0,可向右移动1 d,共4 d。
⑤R(2+5)-R(0+5)=4-5=-1<0,可向右移动1 d,共5 d。
由上述计算结果可知,工序1→3一共可向右移动5 d。资源得到更均衡分配,所有可调整箭线均已调整完成,优化结束,图2为最后优化结果。

图2 第3次调整网络图及资源需求量
5.2 优化方法过程(1次调整)
1)确定非关键线路组。图1中非关键线路1→2→7的总时差相等都为6;非关键线路1→3→5→7的总时差相等都为6;所以令1→2→7为一个非关键线路组,1→3→5→7为一个非关键线路组。
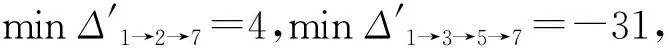
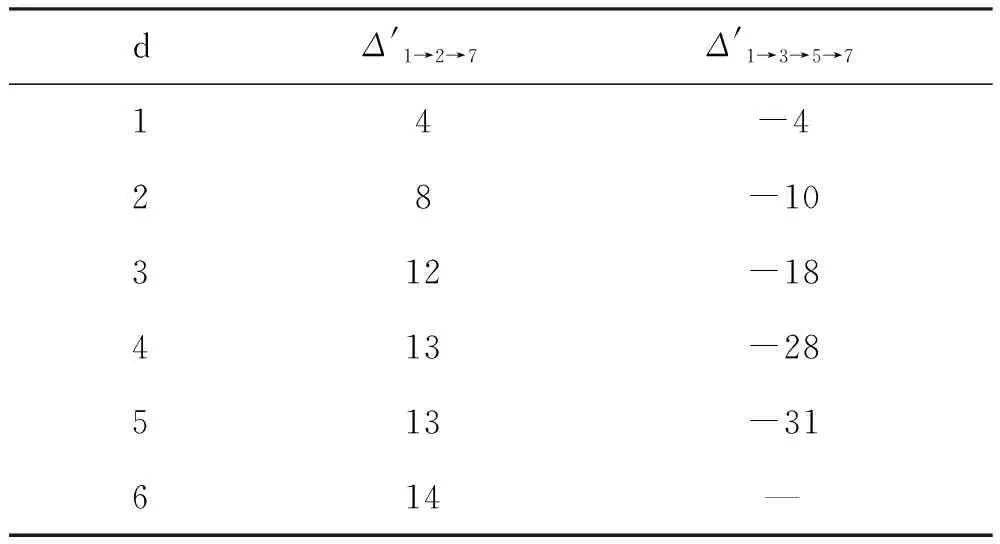
表1 非关键工序组移动后的方差变化值
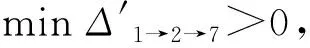

图3 第1次调整后时标网络图及资源需求量
6 结论
改进后的缩方差法其实质就是将原优化过程许多中间环节进行合并、化简。例如引入的非关键工序组方法,将多个可一起移动的非关键工序合并进行一起调整,减少了计算的工作量,从而使网络计划资源均衡优化模型得到进一步的完善。引入的最小方差法,针对同一节点有多个非关键工序组进行调整,将方差最小(即对应使资源配置最接近均衡的情况)值对应的移动时间作为调整时间,使资源配置尽可能一次性达到最优。本文更正并完善了缩方差法的判别公式,整合非关键工序组、最小方差法等方法使调优过程变得更加精简,并减少了大量的计算和调整过程。从实例可以得出结论:原始缩方差法需要3次优化调整的资源,改进后的方法只需要1次即可完成,效率提升了近70%。证明了改进后的方法是切实有效的。
——以某大厦地下停车场第二层开挖管道工程为例*

