“双减”背景下“教学练一体化”的做法与思考——以中考专题复习“探究存在性问题”为例

江苏省南京市六合区教师发展中心 孙德萍

1 引言

“双减”政策落地以来，学生的作业量得到全面压减，但升学压力仍然存在.如何利用课堂这个主阵地提升学习效率，这是“双减”政策给教师提出的重大考验.初三中考复习一般分为一轮复习、二轮复习和综合训练，其中二轮复习一般是以专题复习为主.那么在“双减”的背景下，中考专题复习如何设计呢？笔者以“探究存在性问题”为例，谈一谈“教学练一体化”的做法和思考.

存在性问题是指根据题目所给定的条件，探究是否存在符合要求的结论.此类问题涉及的知识面较广，综合性较强，解题方法灵活，对学生分析问题的能力、应用知识的能力和解决问题的能力要求较高，解决起来有一定的难度，所以一直是各地中考数学试卷常见的压轴题型.

2 精选例题，提高教学的针对性

2.1 特殊关系的存在性问题

例1(由2021年遂宁市中考题改编)如图1，已知二次函数的图象与x轴交于A和B(-3，0)两点，与y轴交于C(0，-3)，对称轴为直线x=-1，直线y=-2x+m经过点A，且与y轴交于点D，与抛物线交于点E，与对称轴交于点F.

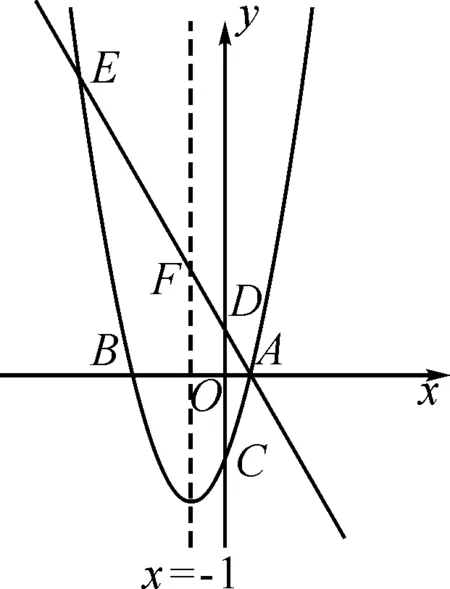
图1

(1)求抛物线的解析式和m的值；

(2)在y轴上是否存在点P，使得以P，D，E为顶点的三角形与△AOD相似，若存在，求出点P的坐标；若不存在，试说明理由.

解：(1)抛物线的解析式为y=x2+2x-3；m=2.

(2)由m=2可得D点坐标为(0，2).建立方程x2+2x-3=-2x+2解得x1=1，x2=-5，所以点E坐标为(-5，12).

假设在y轴上存在点P使得以D，E，P为顶点的三角形与△AOD相似，可分两种情况：

如图2，过点E作EP垂直于y轴，垂足为点P.易得△EDP∽△ADO，求得点P坐标为(0，12).

图2

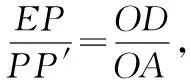
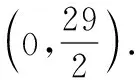
设计意图：本题属于二次函数综合题，涉及相似三角形的判定和性质、解直角三角形、待定系数法、方程思想及分类讨论思想等知识.作为第一个例题主要在于帮助学生弄清什么是存在性问题，如何解决存在性问题，积累分析特殊关系存在性问题的解题经验，提高学生分析问题的能力.

教学说明：对于常见的找一个点使两个三角形相似的问题，一般先假设存在符合条件的相似三角形，然后根据题目条件求点的坐标.本题中△PDE与△AOD相似的对应关系不明确，所以需要进行分类讨论.通过观察两个三角形的特点，发现隐含条件∠EDP=∠ODA，又因为△ADO是直角三角形，由三角形相似的判定方法，可得∠EPD=∠AOD=90°或∠PED=∠AOD=90°.引导学生画出图形，结合图形厘清线段之间的对应关系，从而解决问题.

2.2 特殊图形的存在性问题

例2(2021年重庆市中考题)如图3，在平面直角坐标系中，抛物线y=x2+bx+c经过点A(0，-1)，点B(4，1).直线AB交x轴于点C，P是直线AB下方抛物线上的一个动点.过点P作PD⊥AB，垂足为D，PE平行于x轴，交AB于点E.

图3

(1)求抛物线的函数表达式；

(2)当△PDE的周长取得最大值时，求点P的坐标和△PDE周长的最大值；

(3)把抛物线y=x2+bx+c平移，使得新抛物线的顶点为(2)中求得的点P.M是新抛物线上一点，N是新抛物线对称轴上一点，直接写出所有使得以点A，B，M，N为顶点的四边形是平行四边形的点M的坐标，并把求其中一个点M的坐标的过程写出来.

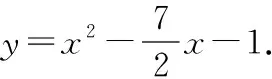
(3)由题意可知，平移后抛物线的函数表达式为y=x2-4x，对称轴为直线x=2.以点A，B，M，N为顶点的四边形是平行四边形分两种情况：

①若AB是平行四边形的对角线，如图4，当MN与AB互相平分时，四边形ANBM是平行四边形.因为AB的中点C(2，0)，所以MN的中点也是点C.由点N的横坐标为2，根据中点坐标公式，可知点M的横坐标也为2，所以点M的坐标为(2，-4).

图4

②若AB是平行四边形的边，如图5，当MN∥AB且MN=AB时，四边形ABNM(或ABMN)是平行四边形.因为A(0，-1)，B(4，1)，点N的横坐标为2，根据平行四边形的对边平行且相等，所以点M的横坐标为2-4=-2或2+4=6，因此点M的坐标为(-2，12)或(6，12).

图5

综上所述，点M的坐标为(2，-4)或(-2，12)或(6，12).

设计意图：存在性问题一般会出现在中考卷压轴题的位置，所以第2个例题选择综合性的压轴题，与例1相区别，考查特殊图形的存在性问题.此类题型经常在二次函数的背景下展开，会运用到方程思想、数形结合思想、分类讨论思想等，对学生的运算能力、思维能力有较高的要求.选用本题的意义在于帮助学生积累解决特殊图形存在性问题的基本策略，提高学生从图形特征入手解决问题的能力.

教学说明：解决平行四边形的存在性问题主要分为两步.首先，根据平行四边形的性质适当分类，确定平行四边形存在的个数并画出符合条件的图形；其次，依据性质求出满足条件的量.本题解答的关键在于完整地画出平行四边形存在的两种情形图，即把已知线段AB作为平行四边形的对角线和边两类.当AB是平行四边形的对角线时，依据“对角线互相平分”和“中点坐标公式”求存在点的坐标；当AB是平行四边形的边时，依据“对边相等”和“两点间的距离公式”求存在点的坐标.教学时要给学生留足时间思考讨论，引导学生结合图形厘清平行四边形的顶点及边的关系，同时教师还要引导学生进行题后反思，归纳总结.

3 提炼方法，提高学习的有效性

存在性问题是近年来中考的热点题型，注重对学生探索性思维能力和创新性思维能力的考查.常见类型有特殊图形的存在性问题和特殊关系的存在性问题，其中特殊图形包括特殊三角形(直角三角形、等腰三角形、等边三角形)和特殊四边形(平行四边形、矩形、菱形、正方形)，特殊关系包括线段、角的等量关系(相等关系、倍数关系)和两个图形之间的关系(三角形全等、相似)等.

在解决存在性问题时，结合题目条件，分析讨论图形结构，常常需要画出示意图，借助几何直观分析，假设存在，再根据条件列出方程或图形特征求解.探究存在性问题的教学，不能只停留在探究具体题目的解法上，而是要在此基础上领会解决问题的方法，形成更具一般性和策略性的解题认识.

“双减”背景下的中考复习课教学，应充分考虑学生的实际情况，减少题目数量，提高题目质量，不求题难，但求提高学生的思维能力，促进知识的迁移，增强应用意识．因此，应以基础性题目为主，既能巩固和复习知识，又能提升学生探究问题的能力，发展其数学核心素养．本设计是存在性问题的专题性复习，既要让学生理解什么是存在性问题，又要让学生体会解决存在性问题的一般方法思路，使学生提高知识的灵活运用能力，发展其思维能力，促进学科素养提升.

4 优化作业，提高练习的实用性

4.1 作业设计

(1)如图6，已知△ABC是边长为3 cm的等边三角形，动点P，Q同时从A，B两点出发，分别沿AB，BC方向匀速移动，它们的速度都是1 cm/s，当点P到达点B时，P，Q两点停止运动．设点P的运动时间为t(单位：s)，解答下列问题：

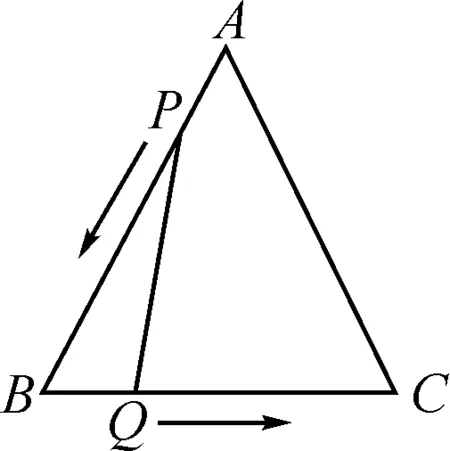
图6

1)当t为何值时，△PBQ是直角三角形？

2)设四边形APQC的面积为y(单位：cm2)，求y与t的关系式；是否存在某一时刻t，使四边形APQC的面积是△ABC面积的三分之二？如果存在，求出相应的t值；不存在，说明理由.

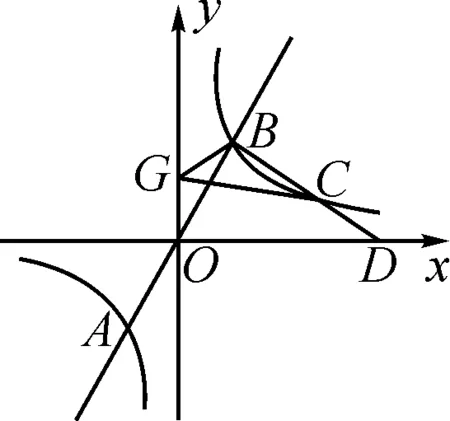
图7

1)求k的值并直接写出点B的坐标；

2)点G是y轴上的动点，连接GB，GC，求GB+GC的最小值；

3)P是坐标轴上的点，Q是平面内一点，是否存在点P，Q，使得四边形ABPQ是矩形？若存在，请求出所有符合条件的点P的坐标；若不存在，请说明理由.

4.2 作业答案

(1)1)当t=1 s或t=2 s时，△PBQ是直角三角形.

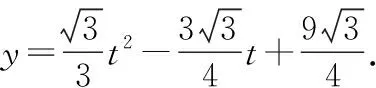
无论t取何值，四边形APQC的面积都不可能是△ABC面积的三分之二.

(2)1)k=6，点B的坐标为(2，3)；

4.3 设计意图

布置作业的目的是为了巩固和理解课堂知识，所以布置作业是有必要的.但是，布置作业应该考虑学情、教学任务、课标要求等因素．在“双减”背景下，数学作业的布置要尊重差异，满足不同层次学生的需要，提倡分层布置作业.作业的第(1)题是中考题的改编题，经过改编后属于中等难度题型，主要考查特殊关系的存在性问题，跟课堂上的例1相呼应，通过此题可了解出学生对特殊关系的存在性问题的掌握情况.作业的第(2)题是中考的压轴题，主要考查特殊图形的存在性问题，与课堂上的例2相呼应，由例2的平行四边形的存在性问题变成矩形的存在性问题，以检验学生的学习效果.

5 “教学练一体化”做法的思考

5.1 优化教学设计，实现高效学习

“教学练一体化”的第一步是教，即教师首先应精心设计科学的教学过程，为后面的学与练打下基础.从备课时的目标定位，到课堂教学时的问题设置，都应充分准备.“双减”背景下的中考专题复习应减少题目的数量，增加题目的质量，注重方法的引导.教师应该有针对性地进行备课和教学，学生已经会的不讲，讲了学生也不会的不讲.在教学中应看到学生的差异，承认学生的差异，做到因材施教，分类指导.“教学练一体化”的第二步是学.“双减”背景下的课堂是以学生为主体的课堂，教师要将自己的“教”与学生的“学”进行结合， 应把“教为中心”转变为“学为中心”，让学生能主动学、学会学、自主学是整个 “教学练一体化” 模式有效实施的关键.所以课堂实践中教师应组织、引导和帮助学生学习，做学生学习的组织者和推动者.

5.2 注重练习反馈，完善评价机制

“教学练一体化”的最终环节是练.这一环节是检验学生学习效果的重要一环.教师教学之后，让学生通过练习来巩固知识，形成技能.“练”是课堂教学的巩固与延续，也是提高学生学习能力的重要一步.“双减”背景下，教师还应注意 “练”的目标要明确且有深度，做到少而精，针对性强.另外，要完善“练”的评价机制，多样化且具有激励性；要注重过程性评价，学习状态和进步程度都可以成为评价的主要内容，通过积极鼓励的评价方式激发其学习欲望.总之，要让学生在课堂中 “练”得轻松，“练”得有效.