环环设问把握本质 步步探究提升素养
——“无刻度直尺网格作图——垂直平分线”的课堂实录与思考
湖北省武汉市吴家山第二中学 李幽兰 尹姝畅
湖北省武汉市吴家山第三中学 万建光
1 引言
我国著名数学家华罗庚曾说过:“形缺数时难入微,数缺形时少直观.”几何直观可以帮助学生直观地理解数学,在整个数学学习过程中都发挥着重要作用.无刻度直尺网格作图题,就是只能用无刻度的直尺在网格中取点、画直线、射线或线段,画出符合题目要求的图形.随着素质教育的不断深入以及试题改革的不断发展,无刻度直尺作图题逐渐受到命题人关注,在近几年的中考试题中频频出现.
2 内容与地位
无刻度直尺网格作图这类题目需要学生具备较强的几何知识的思维能力和综合运用能力,既考查学生的几何直观、推理能力,又考查学生的应用能力和创新能力,促进学生的核心素养的形成[1].
《义务教育数学课程标准》中明确要求,学生能用尺规作出一条线段的垂直平分线,过一点作已知直线的垂线.本节课是基于人教版八年级数学上册前三章内容的期中复习专题课,将三角形全等的性质与判定、线段垂直平分线的性质与判定、等腰三角形的性质等知识有机融合,探究作线段垂直平分线的基本方法,培养学生识图与作图的能力.
3 教学目标与重难点
本节课的教学目标:
(1)掌握运用无刻度直尺作已知线段垂直平分线的基本方法;
(2)解决线段垂直平分线的作图问题,增强学生几何直观及操作的能力;
(3)渗透转化的数学思想,提升学生几何综合素养.
本节课的重难点:掌握运用无刻度直尺作已知线段垂直平分线的基本方法.
4 课堂实录
4.1 导思求学
师:同学们,今天这节课我们一起来学习“无刻度直尺网格作图——垂直平分线”,首先回顾一下线段垂直平分线的定义.
生1:经过线段中点并且垂直于这条线段的直线,叫做这条线段的垂直平分线.
师:回答正确.作线段的垂直平分线,必须抓住两个要点:中点和垂直.“磨刀不误砍柴工”,在学习如何作线段垂直平分线之前,我们先来弄清楚怎样在网格中作出线段的中点和垂线.
基本作图1:作线段的中点.
在正方形网格中,有如图所示(图1、图2)的线段AB,请用无刻度直尺作出线段AB的中点C.仅用无刻度的直尺在给定网格中完成画图,画图过程用虚线表示,画图结果用实线表示.

图1
图2
学生发现作法,教师点评:根据格线的平行或垂直关系取格点构造“8字形”三角形全等是网格中作线段中点的基本方法.构造8字形的取点方式不唯一,作线段中点的方法也不唯一.
基本作图2:过已知点作线段的垂线.
请在图3、图4中用无刻度直尺分别过点B和点C作BD⊥AB,CE⊥AB.

图3

图4
师:如图3,当线段AB在格线上时,点B所在的竖格线上的点都满足BD⊥AB,点C所在的竖格线上的点都满足CE⊥AB.如图4,当线段AB不在格线上时,如何作垂线呢?在作图前,我们先来思考一下,如图5,如果将矩形AGBF绕点B逆时针旋转90°,得到矩形DMBC,则旋转前后的对角线AB和BD有什么位置关系?为什么?

图5
师生活动:学生观察思考,易说明AB⊥BD,直线BD即为过点B所求的垂线.
追问:那么如何过线段外格点C作CE⊥AB?
生2:可以将刚才得到的线段BD平移,平移后的线段还是与AB垂直,点B向下移2格是点C,所以点D向下移2格就是点E,连接CE,直线CE即为所求AB的垂线CE.
师:非常精彩!我们观察到线段AB“横2格,纵3格”,它的垂直线段BD和CE都是“横3格,纵2格”,所以我们可以归纳得出:线段“横a纵b”的垂直线段为线段“横b纵a”.
设计意图:通过两个基本作图,学生掌握网格中线段在格线上、线段不在格线上的中点作法和过一点作其垂线的基本方法,为下一环节作线段垂直平分线做好准备.
4.2 共研释疑
问题1请作出线段AB的垂直平分线CD.(见图1)
生3:图6可以直接取AB的中点C,点C所在的竖格线即为线段AB的垂直平分线.

图6
师:回答非常棒!抓住垂直平分线定义中的两个关键要素:中点和垂直.这就是我们在网格中作线段垂直平分线的基本方法和基本思路.方法(1):取中点作垂线.
追问:对于图7,线段AB的长度为5个单位长度,它的垂直平分线怎么画呢?中点怎么取?垂线怎么画?

图7
生4:(展示作图)可以构造8字形全等三角形来取中点,作垂线的话可以同样方式再取一个满足条件的点.
师:活学活用不错哦!既然我们可以取出垂直平分线上(与线段两端点距离相等)的1个点,那么我们也可以取出2个这样的点,而且不限于在格线上,在方格内可以通过连小正方形对角线的方式找到其中心(如图8),因此得到方法(2):取2个到线段端点距离相等的点再连线.

图8
问题2当线段AB不在格线上,如何作它的垂直平分线?
师:我们可以很容易画出线段的中点和垂线,有什么方法使线段的垂线经过中点呢?
师生活动:学生小组讨论,交流作法,然后展示(如图9-1,9-2).

图9-1

图9-2
教师对学生的作法给予正面评价,指出需注意的问题,引导学生比较这几种方法,总结出作线段垂直平分线的方法(3):平移已知垂线经过中点.注意找到线段平移前后对应点的对应关系.
问题3如果改变网格的行列数,又怎样作线段AB的垂直平分线呢?
师生活动:学生独立思考,交流讨论,展示作法.引导学生联系前面总结的方法,作出线段AB的一条垂线EF,然后平移这条垂线经过中点C,得到所要求的垂直平分线,如图10-1;进一步引导学生将△ACE绕点C顺时针旋转90°得到△DCF,确定点D的位置,连CD即可,如图10-2.这就是方法(4):旋转三角形作垂线.

图10-1

图10-2
设计意图:通过问题1,2,3的作图,学生掌握在网格中用无刻度直尺作线段垂直平分线的基本方法,即主要是平移和旋转这两大图形变换的应用.其中图10-1和图10-2可转化为基本作图,渗透化归的思想方法.学生在动手实践和小组交流中感知无刻度直尺作图的解题特点,经历知识和方法的生成过程,从而探究发现和总结方法.
4.3 拓展应用
(2021武汉中考第20题)如图11是由小正方形组成的5×7网格,每个小正方形的顶点叫做格点,矩形ABCD的四个顶点都是格点.仅用无刻度的直尺在给定网格中完成画图,画图过程用虚线表示.

图11
在图12中,先画△BCD的高CG,再在边AB上画点H,使BH=DH.
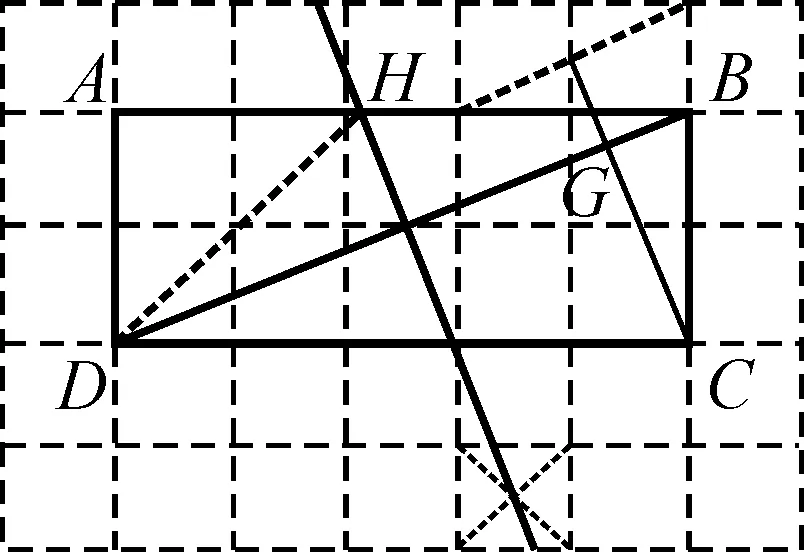
图12
师生活动:学生交流作法,展示作法,如图12.教师引导学生明确解题思路,对学生的作法给予肯定评价,掌声鼓励,并做相关补充.
设计意图:这道题目是2021年武汉中考第20题第(2)问,虽然有一定难度,但通过本节课内容的铺垫和学习后,学生较易读懂题目的意图,明确解题思路,攻克中考题目,体会成功的喜悦,感受“学习有用的数学”.
4.4 总结归纳
师:通过本节课的学习,简单谈谈你的收获.
师生活动:学生分享收获,学生之间互相补充,教师积极引导、评价.
设计意图:回顾这节课学习的知识和方法,加深对所学知识的理解,培养学生善于总结的良好习惯.
5 教学启示与思考
5.1 注重知识的“生长点”与“延伸点”
选择恰当的问题是学生有效参与课堂的关键.虽然学生熟悉线段垂直平分线,然而要在网格中用无刻度直尺作出线段垂直平分线还是存在较大难度.在设计这堂课时,教师由浅入深,引导学生紧扣垂直平分线的定义,分线段在网格的格线上和不在格线上两种情况探讨,最后减少网格数逐步增加难度,总结平移和旋转两大基本方法.让学生在环环递进的问题中体会图形的联系与变化,在动手实践过程中积累活动经验、展现思考过程、交流收获体会、激发创造潜能.从低起点的问题先导、系统化地建构联系,到螺旋式上升的变式拓展,多维度的深度融合,契合学生的最近发展区,实现知识的生成习得与延伸拓展.
5.2 注重知识的理解生成与应用内化
数学知识的教学,应注重学生对所学知识的理解,体会数学知识之间的关联.对于尺规作图,学生不仅要知道作图的步骤,而且还要知道实施这些步骤的理由.为了帮助学生真正理解数学知识,教师从考虑教学内容的特点出发,组织学生开展作图操作活动,引导学生思考分析,运用知识判断不同情形的不同作法,总结概括方法,思考几种方法之间的联系,建立起学生的学习经验与数学知识生成过程之间的联系,让学生真正理解知识,印象深刻.
5.3 注重教会学生学习方法和总结方法
授人以鱼不如授人以渔.传授学生知识,不如传授学生学习方法;传授学生学习方法,不如引导学生自己总结方法[2].本节课的目的并不局限于教学内容,教师以知识为载体,教会学生思考和分析问题的方法,培养学生解决问题的能力,养成总结的习惯.
6 结语
教师要善于将教师的“教”和学生的“学”结合起来,在环环设问和步步探究中发挥学生的主观能动性,提升学生的思维能力和几何素养,重视学生知识的架构和方法的生成,让学生成为学习的主人.

