指向学生关键能力的初中数学学程设计研究*

江苏省宜兴市丁蜀实验中学 滕萍萍

1 引言

初中数学主要培养学生七大关键能力，要求学生能够通过数学知识的学习，提高逻辑思维能力，学会运用数学的眼光和方法分析问题，进行知识迁移.只有具备了数学关键能力，才能提升数学学科的核心素养，实现数学学科的育人目标.

初中数学课堂的教学面向的是全体学生.在学程设计上要关注学生的不同发展水平和认知特点，注意慢化教育，关注学生的反馈，落实教学效果.教师首先要从知识的整体层面进行思维建构，关注核心知识，进行相应的总结和反馈；其次在教学过程中，从创设情境活动、探究建构知识联系、拓展衍生思维发展、互相激发思维四个层面进行学程设计；最后以学生对所学知识进行总结，并结合知识拓展总结解决的思路、经验等，以笔记或者手账的形式进行课堂展示.这样的学程设计可以满足学生的个性发展需求，提升逻辑思维能力和数学建模能力，在学生自主学习的基础上达到举一反三的作用，使学生由一木见森林，提升关键能力[1].本文中以数学正切知识点为例进行学程设计的研究，与各位同仁交流.

2 慢化学程模式的展开过程

2.1 知识点检测反馈

案例1如图1，正方形ABCD的边长为4.对角线为BD，在对角线上有一点E，并且∠BAE等于22.5°，EF与AB垂直，垂足为点F，求线段EF的长.

图1

解：在正方形ABCD中，

∵∠BAD=90°,∠BAE=22.5°，

∴∠DAE=67.5°，

又∵∠ADB=45°，

∴∠AED=180°-∠DAE-∠ADB=67.5°,

∴AD=ED=4.

∵EF⊥AB，∠ADB=45°，

∴△BFE为等腰直角三角形，

设计意图：这道题改编自一道中考题，原题是作为试卷的压轴题考查学生综合应用知识的能力.在新课讲授中，笔者将其改编并作为新课的导入与知识点的检测反馈，考查学生知识的掌握情况，以避免学生猜答案的可能性.由于这道题在解决过程中需要运用到直角三角形的边和角的关系，因此通过这道题引入新知，为本课研究锐角三角形的函数模型作了铺垫，成为其中一种特殊的形式，从而为新概念的学习做好思维铺垫.这样的学程设计有利于新旧知识顺利过渡，培养学生知识迁移的能力，提高知识应用意识.

2.2 自主学习

第一环节:创设情境，搭建新旧知识过渡的思维桥梁，为新知的学习做好可以借鉴的知识准备.

师：刚刚在解决问题的过程中运用到直角三角形，大家想一想直角三角形除了直角以外还有哪些元素？在直角三角形的边与边以及角与角之间还有什么关系？我们已经学过哪些相关的知识？还需要研究哪些新的知识呢？

生1：直角三角形除了直角还有两个锐角和三条边.我们根据直角三角形的性质已经知道了两个锐角的和为90°，两条直角边的平方和与斜边的平方相等.但是，锐角与直角三角形的对边、邻边以及斜边的关系还不知道，需要进一步研究.

师：我们在之前的学习过程中学过哪些特殊的直角三角形？在这些特殊的直角三角形中，它们的边和角有什么特定的关系？请同学们用图形来表达.

师：很好，现在我们已经知道了特殊的直角三角形的边角之间存在可以量化的关系，那么这样的关系能不能推广到一般的直角三角形呢？一般的直角三角形的边和角之间又具有什么关系呢？有没有规范的数学语言的表达方式？下面我们就进入到本课的学习内容“锐角三角函数——正切”.(教师板书本课的课题)

设计意图：在这一环节中，教师整合各学习小组在预习过程中提出的问题，对学生自主学习过程中的问题进行了反馈和补偿.这些问题涉及到的知识点分布在教材的各个环节中.学生通过小组合作，利用集体智慧突破学习难点，使新旧知识建立联系，符合学生的认知特点，有助于学生建构知识体系，是进行慢化教育课堂学程模式的基础[2].学生课前的自主探究学习有利于为即将学习的新知做好思维铺垫，并激发学生的创新意识，有利于新知的学习.

第二环节:框架建构，为建立数学模型搭建思维台阶.

师：同学们仔细阅读课本，总结本课一共研究了哪些问题？教材中是通过什么方法进行研究的？你有其他的研究方法吗？

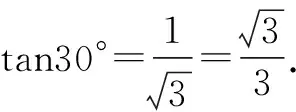
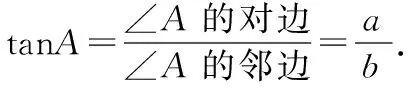
图2

设计意图：引导学生自主阅读教材，分析教材中知识点的讲解方法从而理解编者的思路，进而与自己的解题思路进行连接，激发学生探索新的研究方法.教师从学生的角度进行思维的重组和加工，为学生搭建思维的桥梁，引导学生主动参与研究教材，在自主的思考中理解数学概念，进而学会如何使用数学知识.教师为学生搭建的阶梯使学生能够一步步地水到渠成地理解正切的定义.同时，在教学中，教师将正切线的学习进行前置，从而获取了正切值的一般研究方法，并揭示了正切值在定义域内增减的变化规律.这些思维方式在教学过程中得到了潜移默化的渗透，实现了这一学程模式建立的价值，使学生的思维能力逐步提高.

第三环节:拓展延伸，为感悟数学建模思想提供有效的载体.

案例2如图3，正方形网格中的每一个小正方形的边长都是1，四边形ABCD的四个顶点都在格点上，AD边的中点为点O，假设将四边形ABCD绕着点O顺时针旋转180°，尝试解决以下问题：(1)画出四边形ABCD旋转后的图形；(2)求点C在旋转过程所经过的路径长度；(3)设点B旋转后对应的点为B′，求tan∠DAB′的值.

图3

设计意图：这道题作为联系新知识的有效载体，是因为借助这道题可以实现数学符号语言和图形语言的相互转化.学会数学语言、符号语言和图形语言之间的相互转化是提高学生数学学习能力的关键.本题通过直观的网格图，发展学生的直觉思维，并且渗透数学的构造法和符号化表达，建构起锐角三角函数模型.在慢教育的学程模式下，实现知识的左右连接，上下贯通和知识的序列化，从而固化思维模型.

慢化数学学程模式，重视数学理论的讲解，以丰富的活动载体引导学生反思课堂.学生的自觉反思是深入学习的最好方式，促使学生将所学的知识转化为知识经验和思想方法，从而能够营造数学课堂的学术性，实现数学慢教育的人文价值[3].

第四环节:互动交流，建构数理体系的平台.

师：本课我们学习了哪些知识？是通过什么方法进行研究的？

生3：今天我们学习了有关锐角三角函数的正切概念和如何表示正切的值，并且学习了如何计算锐角的正切值，以及锐角正切值的变化规律.研究的方法是从特殊到一般，从生活的视角出发，渗透数形结合的思想和数学建模思想以及相互转化的方法.

师：很好，那么假设我们猜测编者的意图，你们觉得接下来还会研究哪些问题呢？

生4：我想还会继续研究直角三角形中锐角的对边与斜边的比，以及邻边与斜边，邻边与对边的关系.

师：那么还会在一般三角形的研究吗？请大家课后查找资料进一步调查研究.

设计意图：学生在反思和学习过程中结合教师的引导、点拨，推动了学生学术能力的提高，提升了数学素养，使数学研究回到了教育的本质，即离开课堂之后即使忘了数学知识还能留下数学思想.

3 结束语

数学学程模式的建构突出了学生的主体地位，使教师发挥出适度的引导、点拨的作用，在教学过程中逐渐渗透数学思想和方法，实现数学教学长期目标的落实.