基于耗能保险丝的桥梁双柱墩减震控制研究

秦洪果， 李 萍， 石 岩， 王 瑞

(兰州理工大学 土木工程学院， 兰州 730050)

钢筋混凝土桥梁双柱墩在中小跨径公路桥梁和城市高架桥中被广泛应用，历次破坏性地震中双柱墩也表现出较高的易损性[1-5]。例如，2008年汶川大地震中，强震区(IX～XI度)内20%简支梁桥的双柱墩和40%连续梁桥的双柱墩遭到严重破坏或完全失效。桥梁双柱墩的严重损伤甚至倒塌给抗震救灾造成诸多不便，也给震后交通网的恢复带来极大的经济压力，故提升双柱墩的抗震性能显得尤为重要。

近年来，基于保险丝损伤控制的设计理念逐渐发展，旧金山奥克兰海湾大桥主塔塔柱间的剪切连杆率先实现了桥梁工程领域的保险丝构件设计[6]。在桥梁墩柱的损伤控制方面亦有一定的关注：El-Bahey等[7-8]将保险丝引入到桥梁双柱式排架墩来提高其抗震能力，利用防屈曲支撑(buckling restrained brace,BRB)作为保险丝构件提供了附加强度与刚度，以及通过滞回耗能作用使双柱墩在地震中保持弹性；谢文等[9]对安装BRB、剪切连梁的双柱墩进行了理论分析和试验研究；孙治国等[10]通过拟静力和增量动力分析研究了BRB减小排架地震损伤的效果；石岩等[11-12]发展了保险丝体系的弹塑性反应谱并应用于双柱墩的减震设计，还对比了不同形式BRB对双柱墩的损伤控制效果，以及关键参数的最优取值范围。

目前在桥墩结构领域，保险丝构件主要采用单斜式或人字形布置的BRB，而BRB本身为位移相关型的耗能减震装置，其耗能能力取决于BRB两端的相对位移。但是，钢筋混凝土双柱墩的变形能力本身较小，而BRB按单斜式或人字形布置时其核心段的变形还小于墩柱的水平横向位移，故难以充分发挥BRB的变形和耗能作用。为此，如何使耗能减震装置充分发挥作用，从而较大程度地提高结构的整体减震效果，倍受国内外学者的重视[13]。Constantinou等[14]提出了肘节式和剪刀式的耗能支撑系统，并将其应用到刚性系统和小变形结构中。Hwang等[15]提出了肘节式耗能支撑系统的新设计公式，考虑了阻尼器端部之间的相对垂直变形。可见，当前对位移放大耗能减震系统的研究主要集中在建筑结构领域，但在桥梁工程中的应用甚少。

本文将肘节式BRB耗能减震系统应用于双柱墩结构，旨在放大BRB的位移反应，从而提升其滞回耗能能力，降低双柱墩的地震损伤。首先，基于保险丝的设计理念，推导出由桥墩材料、几何属性和位移放大系数等无量纲参数控制的BRB核心段长度取值范围表达式，以及位移放大系数与肘节式系统相对坐标和桥墩几何属性的关系式，并绘制位移放大系数的三维等高线图；其次，选择具有弯曲破坏和弯剪破坏模式的双柱墩作为案例进行保险丝设计，建立动力分析模型并选择4种类型的地震动进行增量动力分析；最后，分析了不设BRB以及按人字形、单斜式、肘节式设置BRB体系时双柱墩的地震反应和损伤控制情况。

1 基于保险丝理念的双柱墩减震控制

为提高双柱墩的横向抗震能力，可基于“保险丝”的设计理念在其中设置耗能支撑等措施进行减震控制。由于BRB具有稳定的滞回特性和较好的耗能能力，被认为是比较理想的保险丝构件，在双柱墩体系中应用较多。BRB的耗能能力主要由其核心变形段的长度决定，根据保险丝设计理念，可假设：①保险丝构件先于桥墩屈服，确保BRB尽早进入屈服耗能阶段，从而确定了BRB的核心段长度的最大值；②保险丝构件后于桥墩失效，保证保险丝在地震中一直有效的工作，即可确定BRB核心段长度的最小值。

目前，桥梁双柱墩中主要采用人字形和单斜式两种BRB布置形式，如图1所示。基于上述的保险丝设计理念，可引入一系列与桥梁双柱墩几何参数、材料特性相关的参数，推导得到BRB核心段长度比φ(BRB核心段长度lRC与轴向总长度lRT之比)的有效取值范围。对于墩高一致的规则双柱墩，按人字形布置的BRB，长度比φ的范围为

(1)

按单斜式布置的BRB，长度比φ的范围为

(2)

式中：λ为墩高H与截面直径(高度)D之比；γ为墩柱净间距W与其截面直径(高度)D之比；ξ为与截面形状相关的参数；εFy为桥墩纵筋的屈服应变，εRy为BRB核心段钢材的(名义)屈服应变；εRu为BRB核心段的最大设计应变；δ为桥墩的极限侧移角。

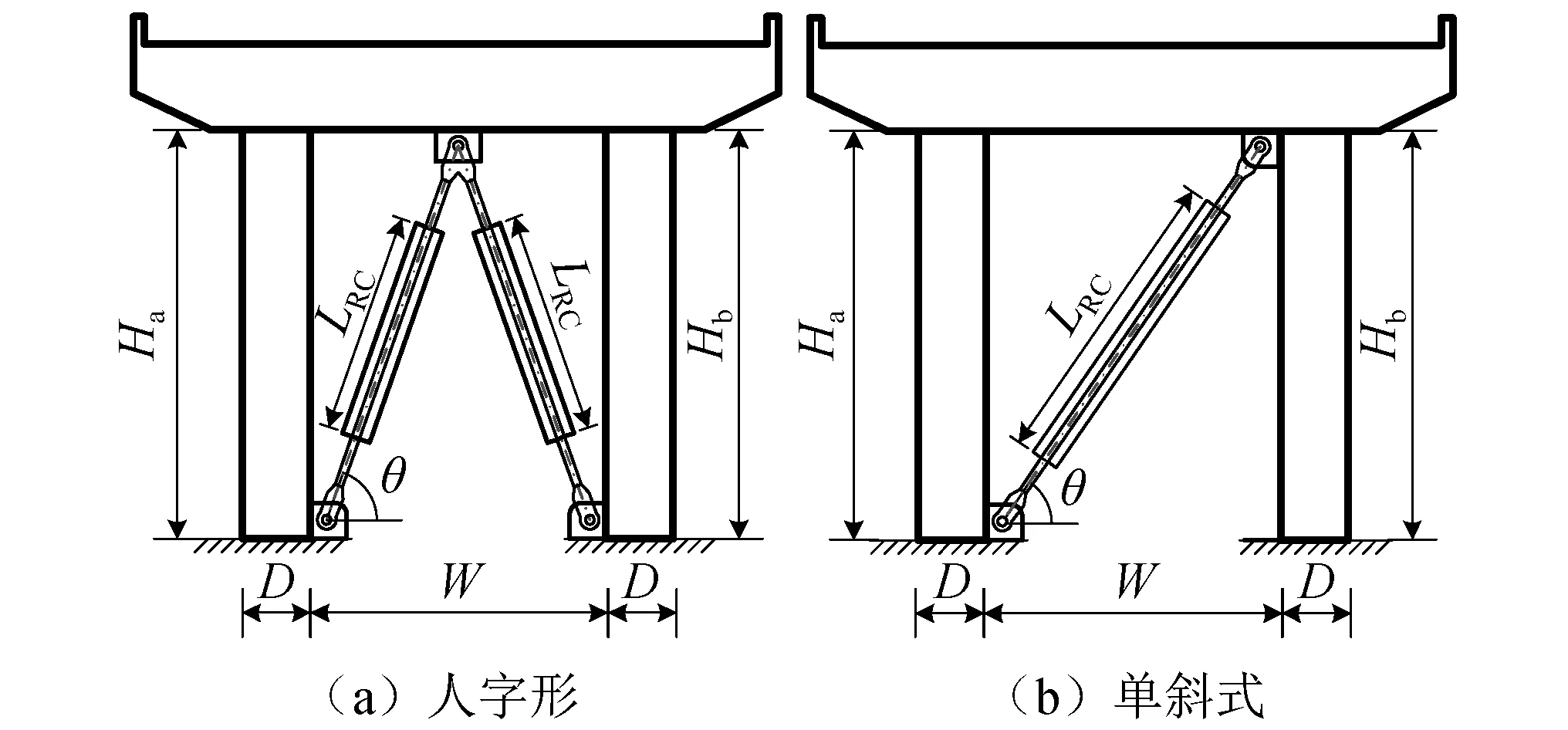
图1 排架墩BRB体系Fig.1 Bridge bent with BRBs

图1所示的人字形和单斜式BRB体系虽能在一定程度上提升双柱墩的横向抗震能力，但对于BRB之类的位移相关型耗能装置，斜向布置时其轴向变形效率相对较低。例如，在双柱墩中按图1(b)以夹角θ=60°设置BRB时，如果双柱墩顶部横向发生1.0 cm的位移，则BRB的轴向位移仅0.5 cm。为此，利用不同原理的机构或机械装置将耗能装置的位移放大，使其在小震作用下也能进入屈服耗能状态，同时在大震中增强其滞回耗能作用，从而可以减少耗能装置的数量，降低减隔震结构成本，取得较好的经济效益。

2 肘节式位移放大保险丝体系设计

根据放大装置的作用机理，将阻尼器响应放大技术分为多种类型。Constantinou等发展了肘节式阻尼器系统，该肘节-支撑-阻尼器系统可细分为上肘节式、下肘节式和反向肘节式3种类型。图2将上肘节式系统应用在桥梁双柱墩中，该体系由一根BRB和两根连杆铰接而成，不同构件间的夹角θ1，θ2和θ3决定其相对位置。根据肘节式体系的设计要求，需满足式(3)和式(4)两个条件时才可对桥墩结构起到有效保护，即

θ≤arctanα

(3)

lAP+lPC>lAC′

(4)

式中：α=H/W；lAP为下连杆的长度；lPC为上连杆的长度；lAC′为点A和点C′之间的距离。

图2 肘节式BRB减震体系及变形Fig.2 Toggle-BRB system and its deformation pattern

2.1 位移放大系数

引入放大系数来评估肘节式支撑系统的放大效率，该放大系数可以从力或位移的角度来定义。本文采用位移放大系数，它反映了耗能装置轴向变形与双柱墩横向位移之间的关系，即

(5)

式中：v为BRB两端之间的轴向位移；u为双柱墩顶部的横向位移。

对于如图1所示的单斜式和人字形系统，如果用放大系数来表达，则f=cosθ；其中，θ是BRB的倾斜角度，这意味着BRB的轴向位移始终小于桥墩的侧向位移，故BRB的耗能能力未能充分发挥。假设桥墩发生小变形，桥墩盖梁和肘节式连杆为刚性，图2所示上肘节式BRB系统的位移放大系数可由式(6)计算为

(6)

只要合理设计该系统，BRB的轴向位移则可能超过桥墩的侧向位移(即f>1)。但考虑到保险丝的设计理念i和j有效性，需进行较为准确地设计BRB核心段长度，以保证BRB先于桥墩屈服。

由于位移放大系数的取值对连接点的位置比较敏感，故引入两个无量纲的相对坐标i和j进行表达，如图3所示。根据结构构造要求，连接点P的容许区域亦可确定。

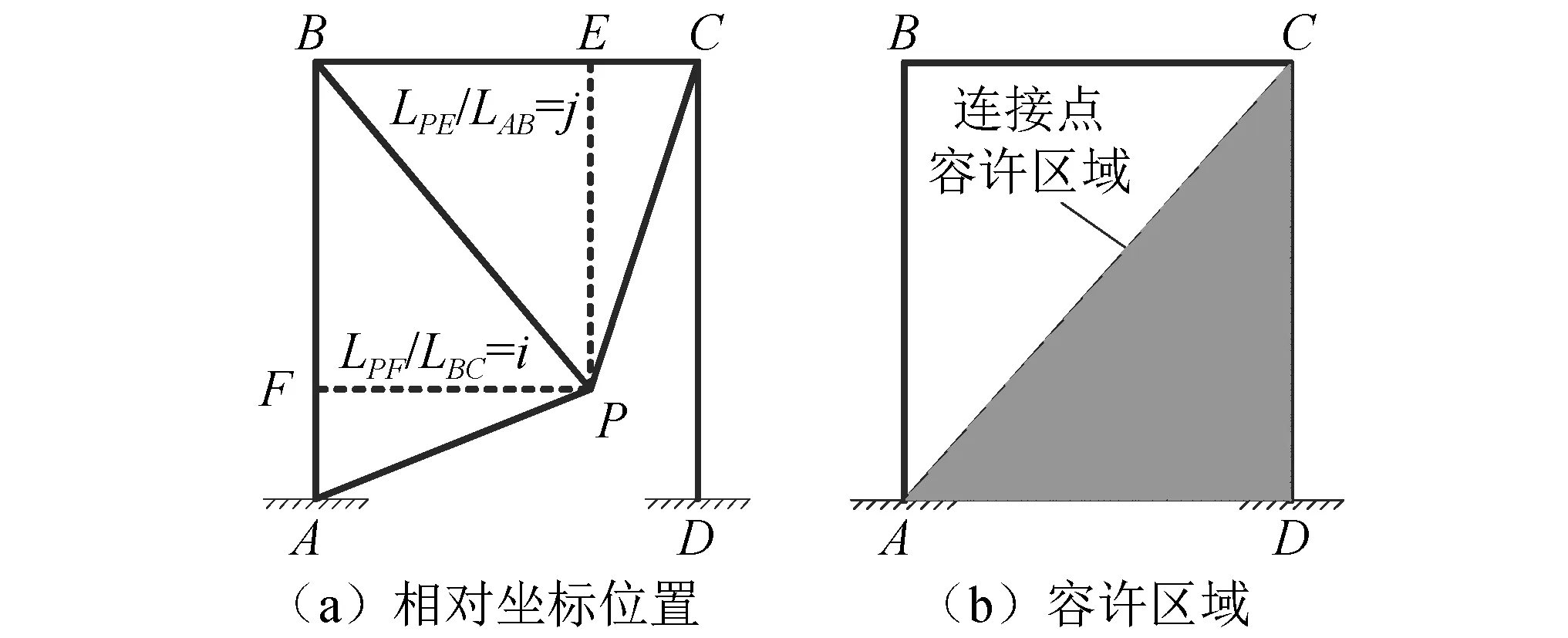
图3 连接点相对坐标及其容许区域Fig.3 Relative coordinates and admissible areas of the connecting point

(7)

(8)

将式(7)和式(8)代入式(6)可得

(9)

需要注意的是：当i=j=1时，肘节式BRB系统转换成单斜式BRB系统；当i+j=1时，连接点位置向对角线方向移动，位移放大系数趋于无穷大。

2.2 BRB核心段长度

与前述结构保险丝的设计理念一致，肘节式体系中的BRB需先于桥墩屈服，使其发挥滞回耗散能量作用，从而保护桥墩结构。由于位移放大的原因，这一条件基本都能满足。再根据BRB在桥墩达到极限位移之前不应破坏的设计原则，可以计算出BRB核心段所需的长度范围。类似于式(1)和式(2)的推导过程，亦可采用φ来表示BRB核心段长度lRC与轴向总长度lRT的比值，从而得到肘节式位移放大系统中BRB的核心段长度的取值范围

(10)

从式(10)可以看出，肘节式位移放大系统BRB的核心段长度比的最小值和最大值整体为无量纲形式，除位移放大系数f、墩柱几何尺寸比(α=H/W，H/D)、以及相对坐标(i，j)外，其他参数的物理意义与式(1)和式(2)相同。相关取值需注意的是：① Upadhyay等[16]认为桥墩接近坍塌性能极限状态时的侧移角δ为2.5%，Xiang等[17]推荐取1.5%，本文取2.0%；②文献[18-19]认为BRB在断裂前可承受3%的循环塑性应变，故εRu取该值；③ξ是与截面形状相关的性能参数，圆形墩柱取2.0～2.5，矩形墩柱取1.9～2.3[20]；④为了实现位移的放大，BRB需要有足够的变形能力，当放大系数f的值太大时，式(10)的左侧的值可能超过1.0，故为图3(a)所示的连接点P找到一个最为合理的位置至关重要。

2.3 位移放大系数等高线图

图4给出了由式(6)计算得到的位移放大系数f三维等高线图。f的设计值是一个常数，可以看作三维空间中的一个平面，当连接点移动到该平面时，f值不会改变。基于式(10)得到φ的取值范围，结合式(6)和图4得到的放大系数，可对双柱墩进行减震设计，得到合理的位移放大系数设计值。

图4 位移放大系数面与设计平面的交点Fig.4 Displacement amplification factor surface and design plane

3 减震控制设计案例与分析模型

为了对比上述3种减震控制措施对桥梁双柱墩抗震能力的提升情况，选择具有不同破坏模式的双柱墩进行保险丝设计，同时通过输入不同类型的地震动记录进行非线性时程分析，探讨了不同减震控制措施的损伤控制效果。

3.1 设计案例

以1座公路连续梁桥中的两个钢筋混凝土双柱式排架墩作为典型分析案例，如图5所示。案例1和案例2的墩高分别为H1=7 m，H2=4.2 m，分别代表了弯曲破坏和弯剪破坏两种破坏模式。此外，其几何尺寸、材料和配筋都相同，墩柱和盖梁分别为1.3 m×1.3 m和1.6 m×1.9 m的矩形截面，都采用C30混凝土、纵筋为HRB335钢筋、箍筋为HPB235钢筋。详细参数见图5和表1所示。

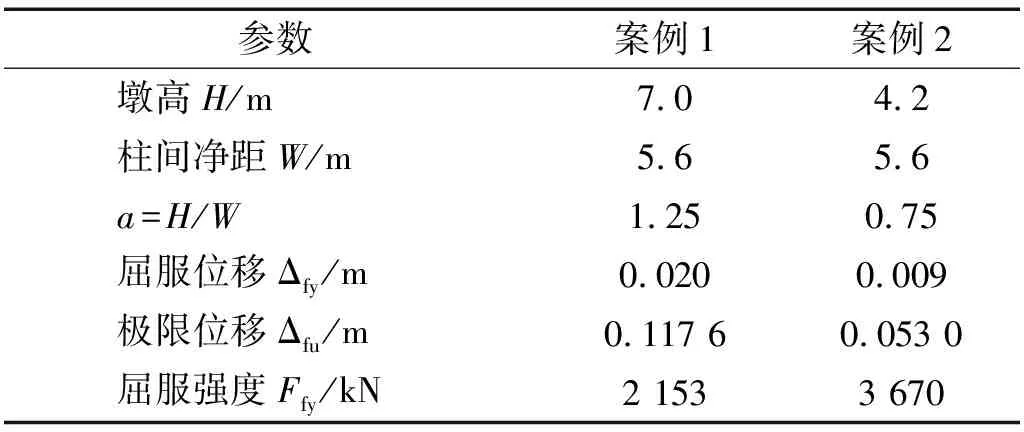
表1 设计案例参数

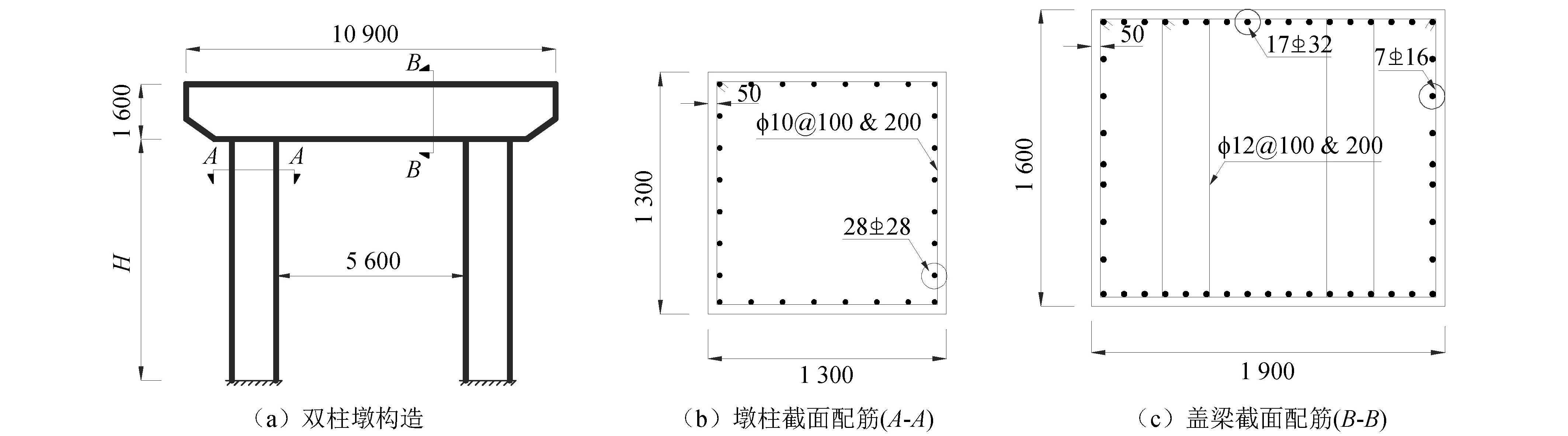
图5 双柱墩构造图 (mm)Fig.5 Two-columns bent and its sections (mm)

3.2 动力分析模型

基于OpenSees分析平台建立了桥梁双柱墩的动力分析模型，盖梁、桥墩用非线性纤维梁柱单元模拟，BRB采用双节点弹簧单元和Steel02材料模拟，屈服后刚度与初始刚度比为2%，连杆则采用刚性桁架单元模拟。案例1桥墩以弯曲变形为主，案例2则需要考虑墩柱的弯剪耦合破坏，采用LeBorgne[21]基于OpenSees开发的Pinching Limit State Material来模拟，通过输入墩柱详细的材料和几何参数程序来自动计算弯曲和剪切特性，并根据墩柱塑性铰区转角来监测剪切破坏的发生时刻[22]。墩底采用固定约束，忽略桩-土相互作用。为突出分析双柱墩及其BRB保险丝体系的减震控制效果，将桥梁上部结构简化为集中质量(M=450 t)并与下部结构刚性连接，忽略了支座非线性特性、主梁与挡块相互作用等因素的影响。双柱墩的动力分析模型如图6所示。

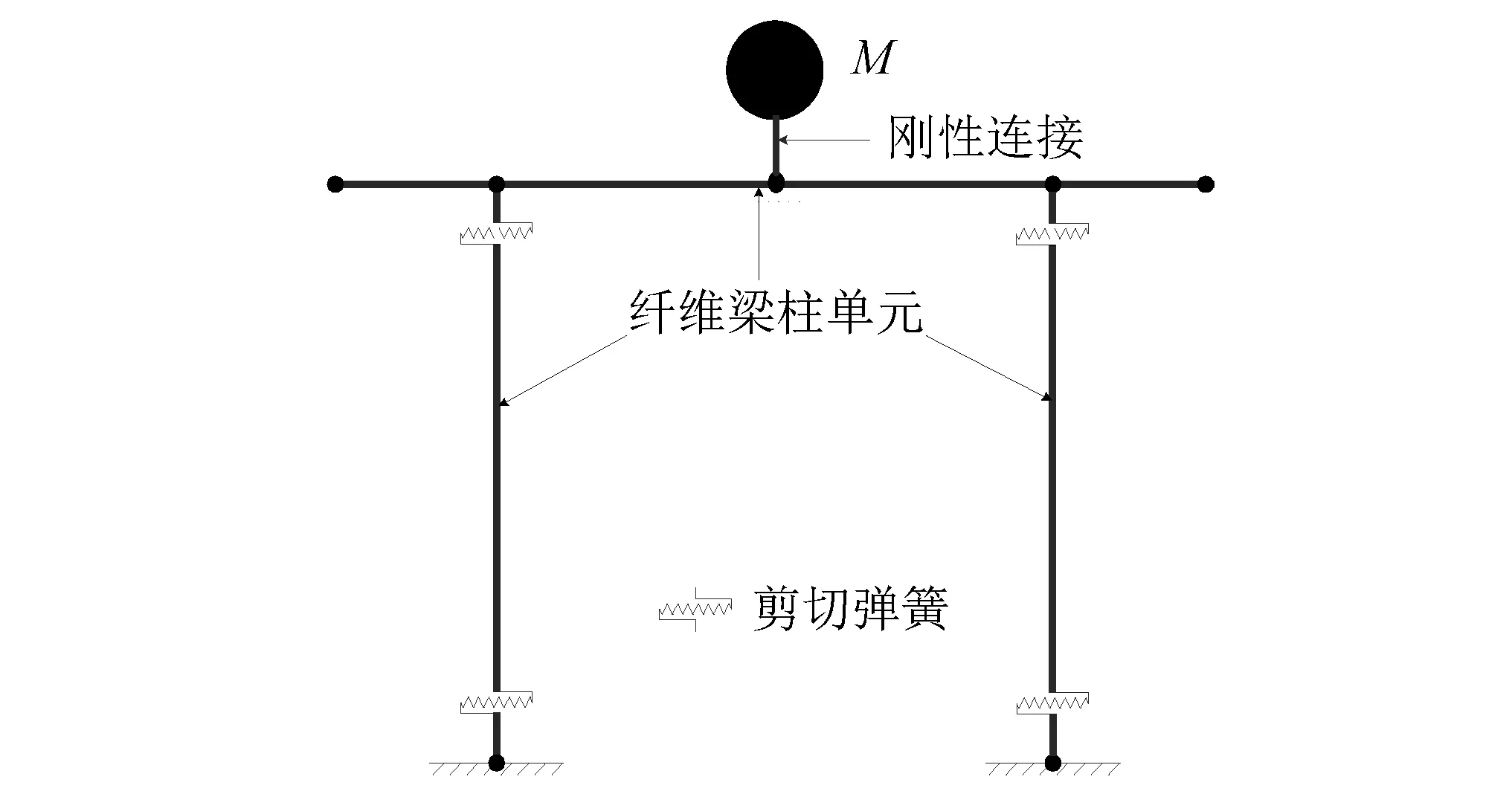
图6 双柱墩模型图Fig.6 Analysis model of two-columns bent

3.3 保险丝体系设计与基本性能

3.3.1 保险丝构件设计

根据肘节式位移放大体系的设计要求，以及式(10)推荐的BRB核心段长度范围，对两个案例进行设计，得到肘节式系统的BRB核心段长度分别为4.711 m和3.917 m，其他性能参数如表2所示。另外，还选择了图1所示的两种BRB布置形式(即人字形和单斜式)；便于对比减震效果起见，BRB构件采用“等强度”和“等刚度”(轴向)的设计原则，即这两种形式的BRB力学性能参数与肘节式一致。

表2 BRB设计参数

3.3.2 双柱墩保险丝体系基本性能

基于建立的分析模型进行往复加载，图7给出案例2剪切效应对滞回曲线的影响，可以发现：剪切破前设置剪切弹簧对双柱墩的滞回曲线影响不大；剪切破坏发生后，双柱墩的强度和刚度则大幅降低。另外，还对两个案例的裸墩及其设置保险丝后的双柱墩体系进行Pushover分析，可得到各自的恢复力曲线及其对应的性能特征点，如桥墩和BRB屈服、混凝土压碎、保险丝失效等，如图8所示。

图7 剪切破坏的影响Fig.7 Influence of shear failure

图8 双柱墩及其保险丝体系恢复力曲线Fig.8 Characteristic curves restoring force

3.3.3 肘节式体系连杆设计探讨

如图2(a)所示的肘节式体系为1根BRB和2根连杆一端铰接相连，另一段与锚固在桥墩上的连接板铰接相连。简化推导起见，前述设计过程和分析模型对连杆进行了刚性假设，但在实际工程中则可能难以实现。为探究连杆刚度对整个肘节式保险丝体系力学性能的影响，特别定义刚度比n来表达连杆刚度与BRB刚度的大小关系，即

(11)

式中：Kb1为BRB初始刚度；Kc1为连杆轴向刚度(假设两个连杆一致)。

对不同刚度比下排架墩保险丝体系进行Pushover分析，图9和图10分别给出了BRB轴向位移和桥墩恢复力曲线，可以看出：随着刚度比的提高，曲线逐渐与刚性响应重合；当n=5时，BRB的变形和桥墩整体恢复力与刚性连杆基本接近。例如，对于案例1的双柱墩当水平推覆位移为3 cm时，5倍刚度连杆与刚性连杆的BRB轴向位移相差8.4%，而桥墩和保险丝整体恢复力相差不超过5%。从推覆结果来看，案例2的相差更小。从工程的角度来看，可以认为当连杆的刚度是BRB的5倍及以上时，基本可满足刚性假设。以案例2为例，其较长连杆除去两端连接段后长度约为2.8 m，若采用I28b工字钢，其刚度便超过了BRB刚度的5倍。

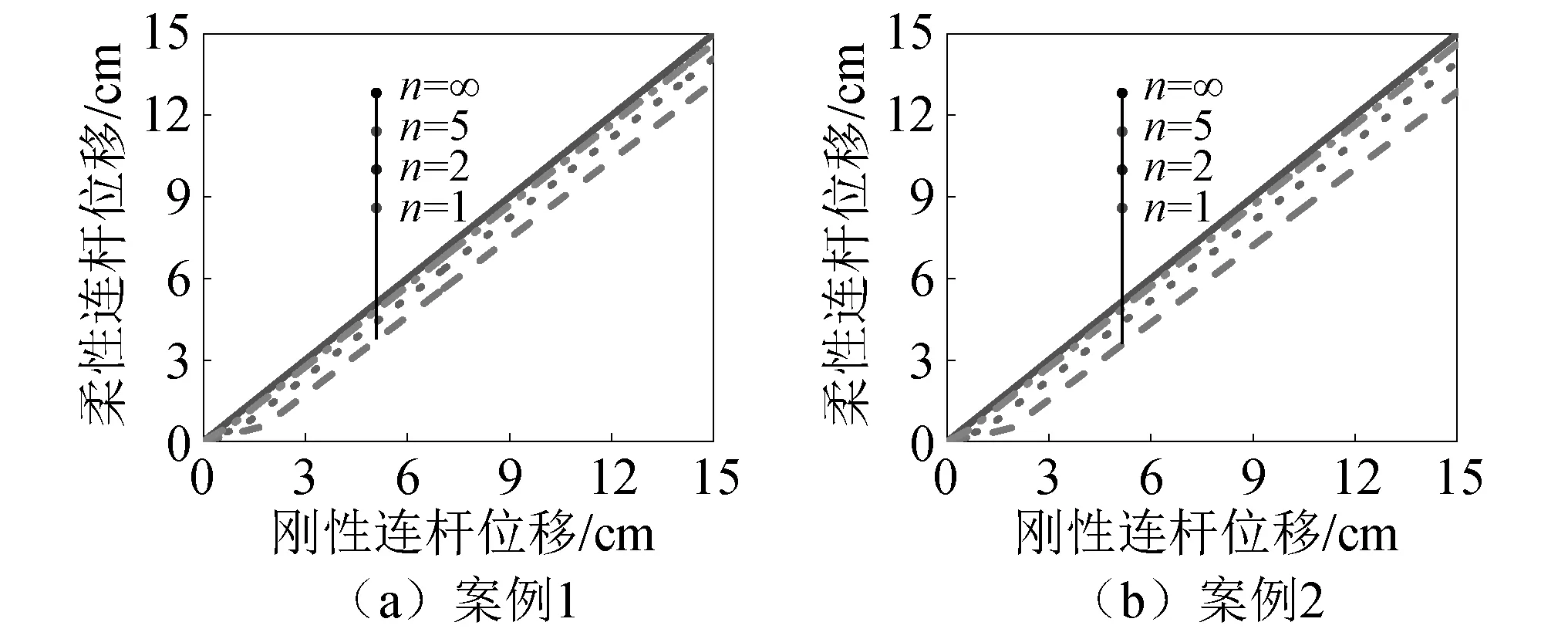
图9 连杆刚度对BRB轴向位移的影响Fig.9 Influence of linkage stiffness on BRB axial displacement

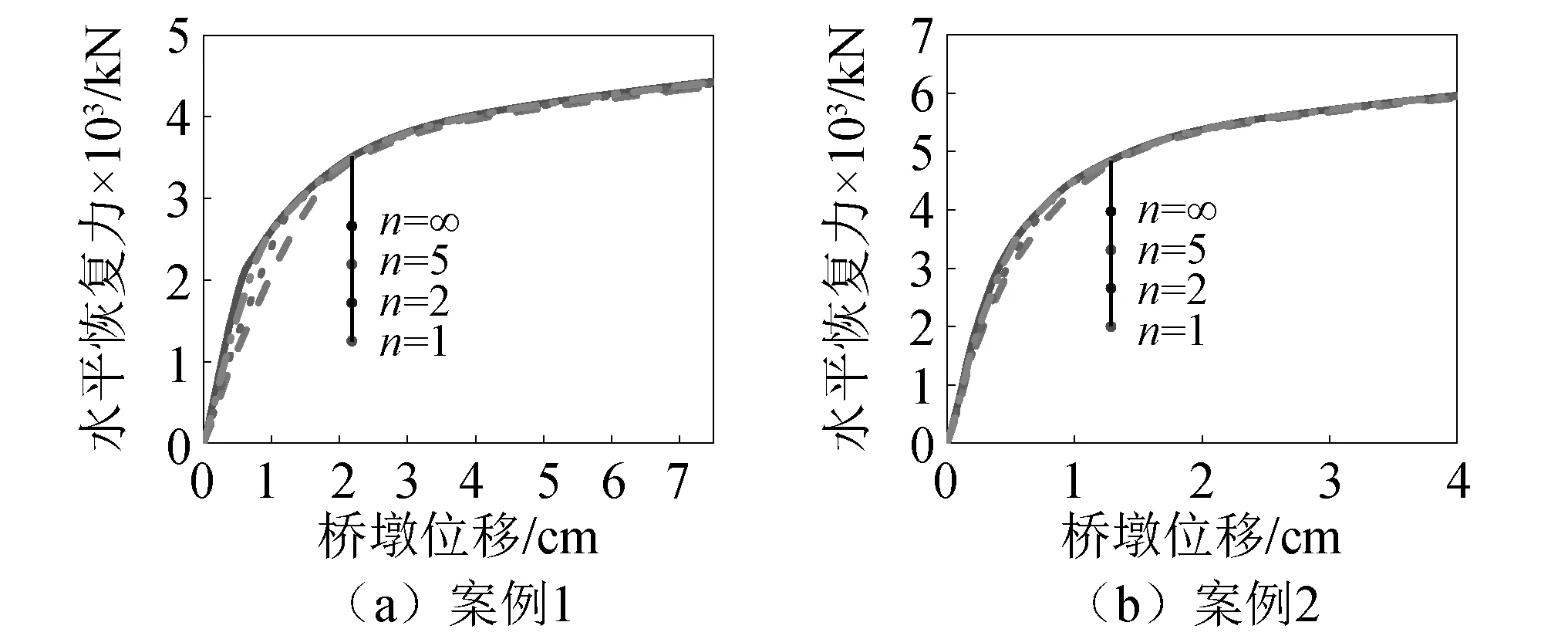
图10 连杆刚度对桥墩恢复力的影响Fig.10 Influence of linkage stiffness on restoring force of bent

3.4 地震动选择

为了解设置不同类型保险丝对双柱墩地震反应的控制效果，选取具有向前方向性效应、滑冲效应的脉冲型和无速度脉冲的3组近断层地震动[23-24]，以及1组远断层地震动[25]沿双柱墩横桥向输入，每种类型的地震动各10条，场地类型主要为D类。放大系数的平均谱如图11所示，可以看出：在长周期范围内具有向前方向性效应和滑冲效应的速度脉冲型地震动的作用强烈，但无速度脉冲效应的近断层地震动和远断层地震动作用在短周期段更加显著。通过调整其加速度峰值(peak ground acceleration,PGA)，以0.1g为步长进行增量动力分析。结果分析时，以每类地震动下结构反应峰值的平均值为讨论指标。

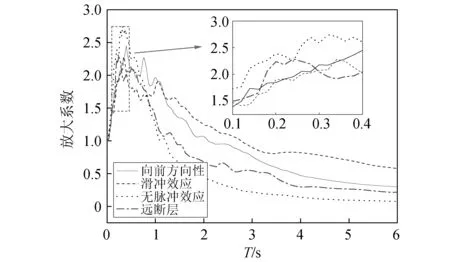
图11 地震动的放大系数谱Fig.11 Amplification spectra of selected ground motions

4 地震反应及减震分析

针对两个设计案例，分别建立不设保险丝的双柱墩模型(下称“裸墩”)以及设置3种形式保险丝(人字形、单斜式、肘节式)的桥墩减震体系模型，以表2所示的BRB作为保险丝，通过输入4种类型的地震动进行非线性动力时程分析。

结构损伤和易损性分析中，通常采用位移延性系数等性能指标表征结构的损伤状态[26]，本文基于文献[27]中以位移延性系数为指标的损伤状态划分区间，以分析设置不同形式保险丝对桥梁双柱墩地震损伤的影响。同时，采用减震率减震装置的减震效果，便采用减震率来表征保险丝系统的减震效果，即定义为裸墩的地震响应峰值和对应减震墩的地震响应峰值之差与裸墩的地震响应峰值之比，表示为

η=(Rn-Ri)/Rn

(12)

式中：Rn为未设保险丝双柱墩(裸墩)的地震响应峰值(每类地震动的平均值)；Ri为设置不同形式保险丝后减震墩的地震响应峰值(每类地震动的平均值)；减震率η越大，表明减震效果越好。

图12和图13给出了案例所示的两个双柱墩在不同强度地震动作用下，未设保险丝的双柱墩(图中的“裸墩”)及采用不同布置形式保险丝时的位移延性系数及其损伤状态。可以看出：

图12 案例1(弯曲破坏)位移延性系数Fig.12 Displacement ductility factors (Case1: bridge bent of bending failure)

图13 案例2(弯剪破坏)位移延性系数Fig.13 Displacement ductility factors (Case2: bridge bent of bending-shear failure)

(1)对于没有设置保险丝的双柱墩(裸墩)，当PGA>0.2g时墩柱开始屈服，即发生了不同程度的地震损伤；当PGA达到0.6g时，墩柱基本达到完全损伤的倒塌状态。但是，当双柱墩设置不同形式的保险丝后，墩柱的损伤明显得到不同程度的降低，如当PGA<0.4g时，设置单斜式和人字形BRB可将双柱墩的地震损伤控制在轻微损伤范围之内(位移延性系数μ<1.2)，而设肘节式BRB系统的双柱墩还未屈服；当PGA增大到0.6g时，滑冲效应作用下的反应最为强烈，桥墩位移延性系数为1.76，才刚进入严重损伤的性能区间，此时BRB应变为0.77%，性能良好。图14和图15分别给出了TCU087-NS和TCU054-EW作用下桥墩和BRB的位移时程曲线和滞回曲线，从图14(a)和图15(a)给出的位移时程曲线可以清楚地看到，设置保险丝构件后对桥墩位移的控制，尤其是肘节式BRB系统将位移反应控制在了弹性状态。

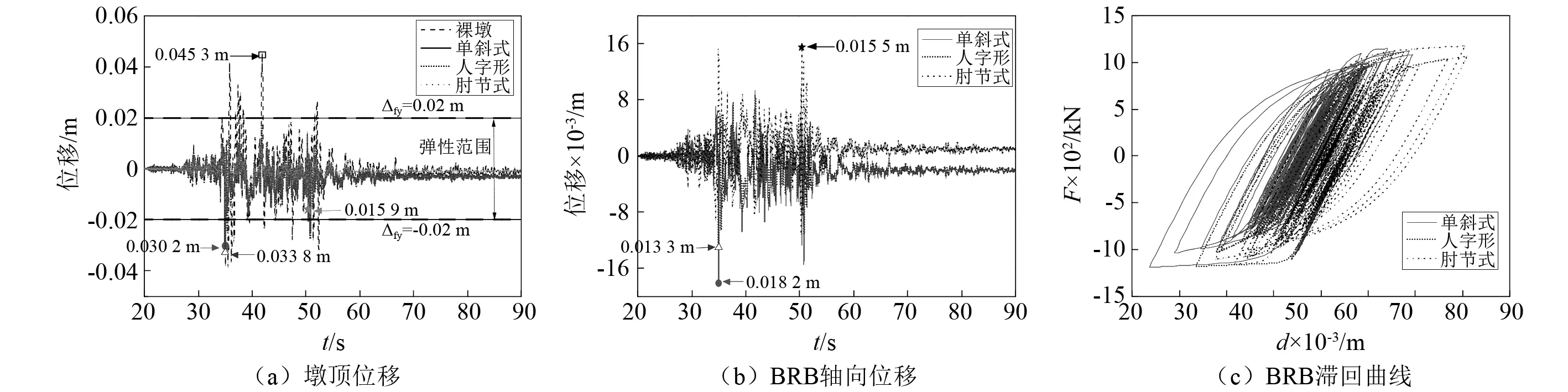
图14 位移时程和滞回曲线(案例1，TCU087-NS，PGA=0.4g)Fig.14 Displacement time history and hysteretic curves (Case1, TCU087-NS, PGA=0.4g)

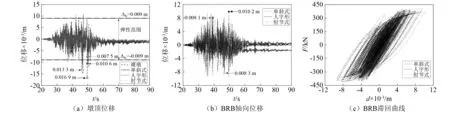
图15 位移时程和滞回曲线(案例2，TCU054-EW，PGA=0.6g)Fig.15 Displacement time history and hysteretic curves (Case2, TCU054-EW, PGA=0.6g)

(2)不同形式的保险丝对双柱墩的减震控制效果差异较大。限于篇幅，图16仅给出了部分滑冲作用和部分强度下保险丝的减震率。从整体的减震率来看，案例1所示的弯曲型双柱墩设置单斜式、人字形和肘节式BRB系统时的减震率分别为：30%～55%，20%～35%和50%～70%，而案例2所示的弯剪型双柱墩的减震率则分别为5%～20%，5%～20%和20%～40%。可以认为，按等强度和等刚度设计下，肘节式BRB系统的减震效果最佳，人字形则最差，主要是由于同等条件下BRB的夹角θ最大，BRB的变形效率较低，而肘节式系统的BRB变形效率则最高。例如，图14(b) 中人字形和肘节式BRB的轴向变形分别为0.013 m和0.016 m，可以认为相差不大，但双柱墩墩顶位移分别为0.031 m和0.016 m(图14(a))，充分说明肘节式系统对BRB位移的放大作用，这也与保险丝设计时的位移放大系数相符(f=1.0)；案例2所示的弯剪破坏型桥墩亦是如此(见图15)。另外，注意到两个案例的减震率相差较大，主要原因是：①两个案例仅墩高有差异，但案例2设置的BRB刚度却较小(见表2)，位移反应自然较大，减震率较低；②采用的保险丝为位移相关型的BRB，减震主要依靠变形时的滞回耗能来实现，而案例2的墩高较低，桥墩的变形相比案例1要小，一定程度上限制了BRB的耗能作用，减震率也随之降低。

(3)地震动类型对双柱墩的反应和保险丝减震率也有一定的影响。当地震动输入强度相对较小(PGA<0.4g)时，不同类型地震动作用下的反应相差不大(见图12和图13)；近断层脉冲型地震动下的反应甚至小于无脉冲型和远断层地震动，主要是由于两个双柱墩及其减震体系都属于短周期结构(0.18～0.37 s)，从图11所示的放大系数谱可以看出该周期段近断层脉冲型地震动的反应略小于其他两类；具有向前方向性效应和滑冲效应的脉冲型近断层地震动主要表现为长周期速度脉冲，对长周期结构的反应更为强烈(见图11)；因此，随着输入地震动强度的增大，双柱墩结构的损伤加剧，随之刚度减小、周期延长，脉冲型地震动下的地震反应和损伤大于其他两类。

(4)弯剪破坏型双柱墩(案例2)的水平刚度较弯曲型(案例1)要大，其屈服位移、变形能力相对较小。对于单斜式和人字形的BRB保险丝体系，即便可以让保险丝先于桥墩屈服，但位移相关型保险丝的耗能需要足够的变形，而且随着保险丝的屈服，整个体系的刚度随之降低、位移需求增大。因此，保险丝在滞回耗能的同时，该类双柱墩结构也会经受较大的地震损伤。但是，肘节式系统放大了保险丝的变形，在同等的桥墩位移和地震损伤情况下，保险丝可以发挥更大的滞回耗能作用(见图13和图15)。可见，肘节式位移放大体系对于高度相对较低，但具有一定弯曲变形能力，最后才发生剪切破坏的双柱墩依然具有较强的适用性。需要说明的是，对于高度非常低的脆性矮墩，发生剪切破坏时的位移非常小，BRB等位移相关型的减震装置难以发挥其滞回耗能作用。

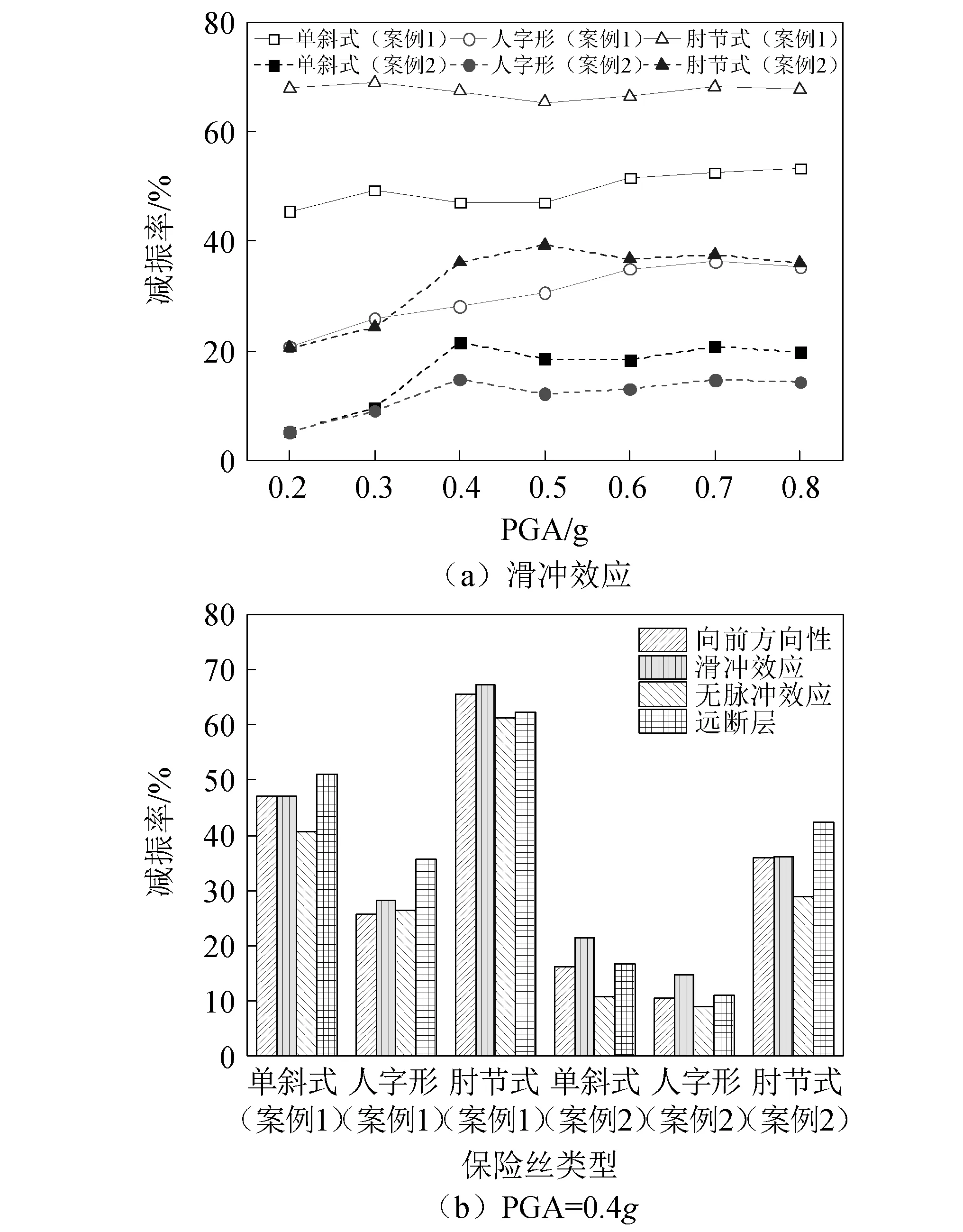
图16 减震率Fig.16 Seismic mitigation ratio

5 结 论

(1)将肘节式位移放大体系应用在双柱墩中，推导出由桥墩材料、几何属性和位移放大系数等无量纲参数控制的BRB核心段长度取值范围表达式，用于双柱墩减震控制设计。

(2)设置单斜式、人字形和肘节式防屈曲支撑对桥梁双柱墩的地震损伤具有明显的控制作用，等强度和等刚度设计下肘节式BRB体系的减震效果最好，按人字形布置的BRB减震效果最差。

(3)肘节式体系的BRB能够充分发挥其变形和滞回耗能作用，可将双柱墩的地震损伤控制在轻微破坏乃至于弹性状态，尤其适用于变形能力相对较弱的弯剪破坏型桥墩。

(4)地震动强度较低时，非脉冲型地震动作用下的反应强烈；但地震动强度较大时，双柱墩结构的损伤加剧，具有向前方向性效应和滑冲效应的脉冲型地震动作用下的反应更加强烈。