平面欠驱动柔性机械臂的PSO轨迹优化与自抗扰振动抑制
潘昌忠, 罗 晶, 李智靖, 熊培银, 陈 君
(湖南科技大学 信息与电气工程学院,湖南 湘潭 411201)
传统工业机器人一般采用刚性结构,存在基座笨重、功耗高、 操作空间有限、负重比低、灵活性差等问题,已经难以满足高精密产品生产和现代化企业的自动化需求[1]。相比而言,柔性臂机器人采用柔性材料制作的柔性连杆结构,具有质量轻、功耗低、工作空间大、负载自重比高、灵活性好等特点[2],在航空航天、工业制造等领域具有广泛的应用前景,受到了人们的广泛关注[3]。然而,柔性机械臂是一类高度非线性、强耦合以及时变的分布参数系统,它具有无限个自由度和有限个控制输入,属于一类欠驱动机械系统[4-6]。有限的控制输入不仅要实现驱动关节的控制目标,而且还要抑制柔性连杆由于运动而引起的弹性振动,否则将严重影响机械臂的定位精度和操作效率[7],而且在外太空等空气阻尼微弱的环境中,这种弹性振动很难自行消失[8]。因此对柔性机械臂进行振动抑制与稳定控制是机器人研究领域的热点难题。
关于柔性机械臂的振动抑制问题,Zhang 等[9]提出了一种基于观测器的边界控制方法,实现了柔性机械臂的轨迹跟踪控制。吴忻生等[10]使用偏微分方程表示的分布参数模型描述柔性机械臂的动态特性,在末端边界基于李雅普诺夫直接法进行控制,降低了机械臂的弹性振动。Liu 等[11]针对具有输入扰动和输出约束的柔性机械臂,利用李雅普诺夫直接法,设计了带有干扰观测器的边界控制器,在调节角度位置的同时抑制弹性振动。然而,这些控制方法除在关节处需要控制输入外,在末端负载处也需要额外的控制输入。
为了实现柔性机械臂仅在关节驱动器作用下的稳定和振动抑制控制目标,杨春雨等[12]根据奇异摄动理论将模型分解为描述刚体运动的慢时间尺度模型和描述柔性变形的快时间尺度模型,通过测量机械臂弹性振动,提出了一种双时间尺度组合控制器。张晓宇等[13]在柔性机械臂两侧粘贴压电传感器和压电致动器,提出一种基于H∞优化的抗扰控制算法。王海等[14]构建了基于压电陶瓷材料的柔性机械臂的主动抑振理论模型,设计了一个可变控制方案的抑振器。娄军强等针对伺服电动机、谐波齿轮减速器、柔性臂及压电致动器组成的智能柔性机械臂系统,提出了一种基于PD控制与模糊控制的复合控制策略。这些控制方法虽然获得了良好的振动抑制效果,但是需要传感器测量柔性臂的角位移,而且需要附加压电传感器检测柔性振动,不仅增加了系统的设计成本,而且使系统的结构更加复杂。Meng 等[15]等利用模糊遗传算法的在线优化能力,提出了一种基于系统能量的智能优化稳定控制策略,实现了柔性机械臂的快速稳定控制。Schnelle 等[16]通过反馈线性化将非线性系统简化为线性系统,提出了一种自适应模型预测轨迹跟踪控制方法。但是,这些控制方法依赖于系统精确的数学模型。当柔性机械臂存在参数摄动、未建模动态及外部干扰等不确定性因素时,控制系统的鲁棒性将难以保证。
针对以上问题,本文以平面单连杆柔性机械臂(planar single-link flexible manipulator,PSLFM)为研究对象,提出一种基于粒子群优化 (particle swarm optimization,PSO) 算法的轨迹优化与自抗扰振动抑制控制方法,实现机器人末端执行器在任意目标位置的稳定控制目标。首先,基于假设模态法和欧拉-拉格朗日公式建立系统的动力学模型,通过分析该模型的欠驱动特性获得驱动变量与欠驱动变量之间的状态约束方程。其次,考虑状态约束关系的影响,利用双向轨迹规划方法,为驱动关节规划一条从初始位置到中间位置的前向轨迹和一条从目标位置到中间位置的反向轨迹,并通过粒子群算法对轨迹参数进行优化,确保两条轨迹平滑地拼合成一条轨迹,从而为系统规划出一条从初始位置到目标位置的期望轨迹,将系统的位置控制与振动抑制问题就转化为轨迹跟踪控制问题。然后,引入线性自抗扰控制(active disturbance rejection control,ADRC)技术,把机械臂的模型参数摄动、未建模动态及外界干扰等不确定性因素看作一个新的扩张状态变量,设计扩张状态观测器和基于状态误差的反馈控制器使系统沿期望轨迹到达目标状态。最后,通过仿真与对比试验,说明所提方法的有效性和优越性。
本文通过把基于PSO的抑振轨迹规划技术与自抗扰控制技术相结合,提出一种基于轨迹规划的前馈控制和自抗扰反馈控制的复合控制策略。与其他方法相比,该控制策略具有以下三个优点:
(1) 不需要额外控制输入,仅使用关节驱动器,同时实现PSLFM的关节稳定控制与弹性振动抑制;
(2) 不使用速度传感器,也不需要检测振动的压电传感器,所设计的控制器仅需要测量角位移的传感器;
(3) 不依赖精确的数学模型,所设计的自抗扰控制器能够保证系统存在不确定性情况下的鲁棒性。
1 PSLFM的建模和问题描述
假设模态法建立的方程计算效率高,便于数值仿真及实时控制,是柔性机械臂研究中的主流方法[17-18]。本章先采用假设模态法与欧拉-拉格朗日公式建立平面单连杆柔性机械臂的数学模型,然后对模型的欠驱动特性进行分析,进而提出本文的控制目标。
1.1 动力学建模
PSLFM的结构模型如图1所示,其物理参数如表1所示。图1中:XOY为惯性坐标;X′OY′为旋转坐标;R为柔性臂上任意点相对于惯性坐标的位置。

图1 PSLFM 的结构模型Fig.1 Structure model of PSLFM

表1 PSLFM 的物理参数
假设该柔性连杆为Euler-Bernoulli臂,并且由于它被限制在水平方向上移动平面上,重力的影响被忽略,那么连杆满足梁的无阻尼弯曲自由振动微分方程
(1)
其中弹性挠度w(x,t)表达为
(2)
式中:pi(t)为第i个时间相关的广义坐标,也称为模态坐标;φi(x)为第i个与空间有关的模态函数
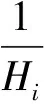
ai[sinh(λix)-sin(λix)]}
(3)

(4)
式中,λi为满足如下特征方程的第i个正解
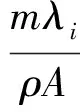
(5)
在实际中,忽略高阶模态对系统的影响,取前n个模态,那么将式(2)重写为
(6)
一般来说,n越大对系统的描述越精确。若模态p1,p2,…,pn都收敛到零,弹性挠度w(x,t)也收敛到零,此时系统将无残余振动。
根据图1的几何关系,位置向量R可以表示为
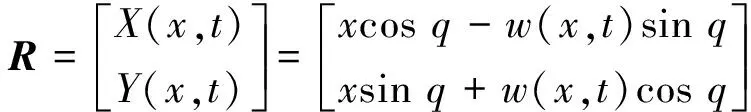
(7)
系统的动能为
(8)
系统的弹性势能为
(9)
式中,ki为系统的弹性系数,可以表示为
(10)
令p=[p1,p2,…,pn]T,θ=[q,pT]T,取欧拉-拉格朗日函数为L=T-D,根据欧拉-拉格朗日方程
(11)
可获得系统的动力学方程
(12)
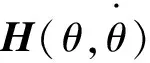
(13)
矩阵M(θ)可以表示为
(14)
式中,矩阵Mqp,Mpp的具体形式为
(15)
式中,σi,ηij,(i,j=1,2,…,n)的表达式分别为
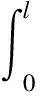
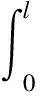
(16)
矩阵Mqq可以表示为
(17)

1.2 问题描述
可以看到,PSLFM建模过程非常复杂,其弹性模态坐标具有无穷维空间,是一类强耦合非线性的分布参数系统,要获得系统精确的数学描述非常困难。另外,从式(12)建立的动力学方程可知,系统有n+1个自由度,但只有一个控制输入,是高度欠驱动的机械系统,其中:q为驱动变量;p为欠驱动变量,它们之间存在强耦合的非线性状态约束关系
(18)
因此,要实现PSLFM的稳定控制与振动抑制,就应该考虑式(18)的非线性状态约束关系的影响,通过控制驱动变量q来间接控制欠驱动变量p,实现q到达并稳定在期望角度qd的同时保证欠驱动变量p收敛到零。
本文的控制目标表述为:对于由式(12)描述的PSLFM,当系统模型不精确时,考虑式(18)的非线性状态约束关系的影响,设计控制律τ使得机械臂驱动关节到达目标角度时,柔性连杆的弹性振动同时得到抑制,即:q→qd,p→0,实现末端执行器从任意初始位置到目标位置的精确稳定控制。
2 振动抑制轨迹规划
为了实现系统的位置控制目标,本章首先为驱动变量q规划规划一条从初始位置到中间位置的前向轨迹和一条从目标位置到中间位置的反向轨迹;然后,采用粒子群算法对轨迹参数进行优化,确保两条轨迹平滑地拼合成一条完整的期望轨迹。
2.1 双向轨迹设计
由于欠驱动变量的存在,直接规划系统从初始状态q0到目标状态qd的平滑轨迹是困难的。本文使用一种双向轨迹规划的方法,它是一种计算简单、操作方便而且效果较好的振动抑制方法。通过选择中间角度qm为驱动变量q规划一条前向轨迹和一条反向轨迹。
根据系统的无残余振动位置控制目标,待规划的期望轨迹应该满足两个边界条件,当系统处于初始状态时,应该满足
(19)
当系统到达目标状态时,应该满足
(20)
因此,给定前向轨迹参数ka,从初始角度q0到中间角度qm的前向轨迹Γ1设计为
(21)
式中:sf=qm-q0;0≤t<1/ka。
给定反向轨迹参数kb,从目标角度qd到中间角度qm的反向轨迹Γ2设计为
(22)
式中:sr=qm-qd;tr=1/kb-t,且0≤tr≤1/kb。
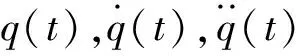
从式(21)与式(22)中还可以看到,qm,ka和kb是轨迹规划中非常重要的一组参数,这三个参数的取值将影响机械臂的跟踪效果,因此为获得更好的跟踪效果,还需要求解出一组最优的参数值。
2.2 基于PSO的轨迹优化
与遗传算法等其他优化技术相比,PSO算法[19]的计算成本更低,需要调整的参数更少。因此,本文采用PSO算法对qm,ka和kb进行智能优化,以确保两条轨迹平滑地拼合成一条完整的期望轨迹,从而将系统的位置控制与振动抑制问题就转化为轨迹跟踪控制问题。

(23)
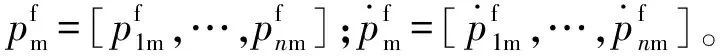
当轨迹Γ2到达中间角度qm时,把式(22)代入式(18)中进行数值求解得到相应的中间位置,记作
(24)
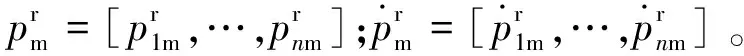
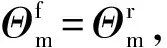
(25)
式中:si=[qm,ka,kb]为第i个粒子的的位置;vi为粒子的速度;Pi为第i个粒子的个体历史最优位置;Gt为群体历史最优位置;N为粒子群的大小;Kmax为最大迭代次数;w为惯性因子;c1,c2为加速常数;vmax,vmin为速度的上下边;smax,smin为位置的上下边界;r1,r2为在[0,1]当中的随机值。
PSO求解算法步骤如下:
算法1:期望轨迹的PSO求解算法

输出:参数qm,ka,kb或最优解Gt
初始化:设置参数N,Kmax,hmin,w,c1,c2,vmax,vmin, 随机初始化粒子群s(0)和初始速度v(0),更新相应个体最佳位置Pt和群体最佳位置Gt。
whileK
fori=1toN
forj=1to3
vi.j(K+1)=wvi,j(K)+c1r1[Pt-si,j(K)]+
c2r2[Gt-si,j(K)]
ifvi,j(K+1)≥vmaxthen
vi,j(K+1)=vmax;
ifvi,j(K+1)≤vminthen
vi,j(K+1)=vmin;
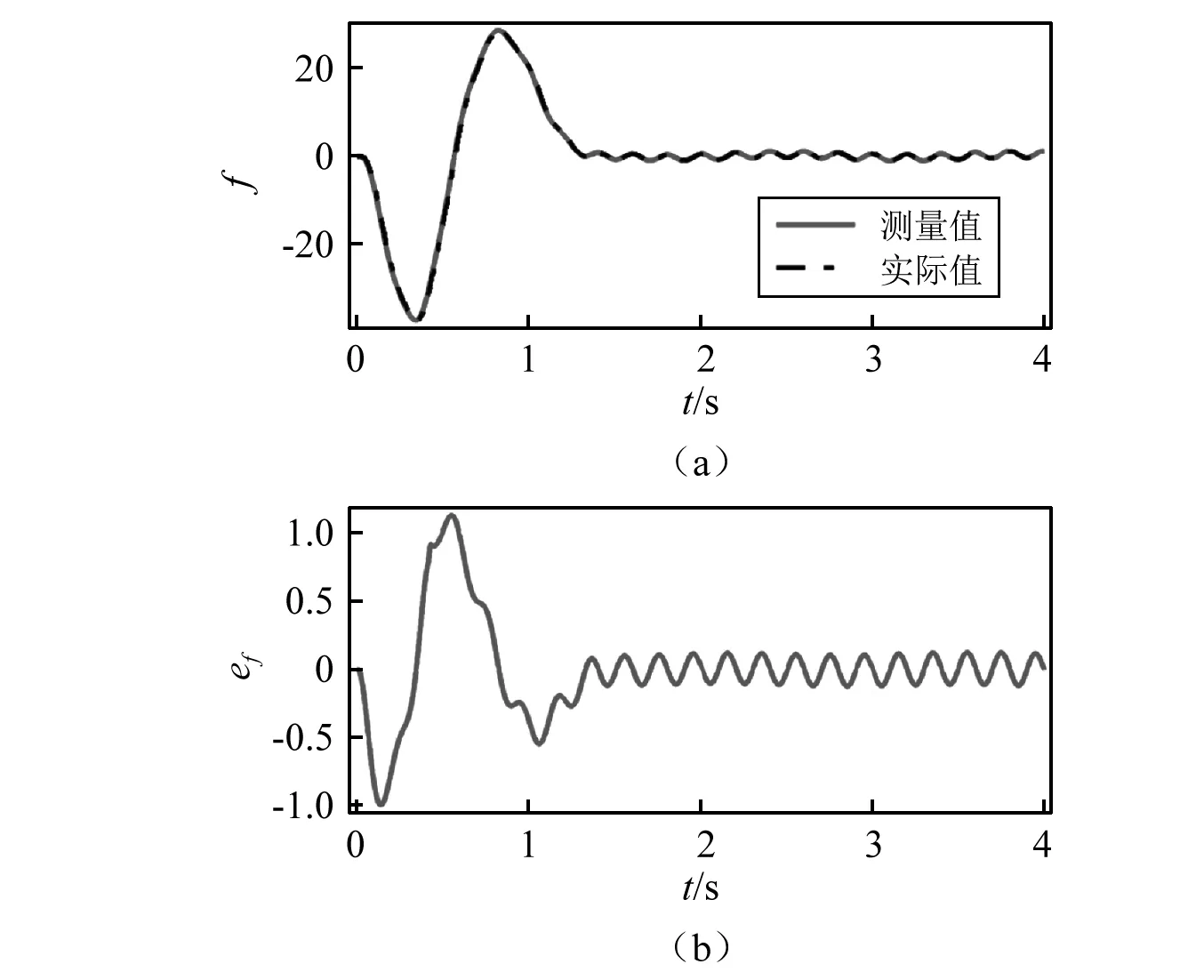
ifh(si) Pt=si(K+1); ifh(si) Gt=si(K+1); K=K+1。 自抗扰控制是在传统PID和现代控制理论的基础上提出的一种不依赖系统模型的控制方法[20]。这种方法在解决非线性和建模不精确的系统等控制问题方面具有广阔的应用背景[21]。因此,本章设计自抗扰轨迹跟踪控制器以实现PSLFM在模型精确时对规划轨迹进行精确跟踪。基于自抗扰控制技术的PSLFM轨迹跟踪控制结构,如图2所示。 考虑式(18)中的非线性约束关系,可以通过控制驱动变量q来间接控制欠驱动变量p。由式(18)得 (26) 代入式(12)可以得到一个驱动变量子系统 (27) 图2 基于PSO和ADRC的PSLFM轨迹规划与跟踪控制结构框图Fig.2 Structure diagram of trajectory planning and tracking control of PSLFM based on PSO and ADRC 为了建立驱动变量子系统的状态空间方程,把机器人的模型非线性项、耦合项归结为系统的总扰动项f,其表达式为 (28) (29) 当状态变量x为已知信息时,为了使式(29)稳定并补偿总扰动f的影响,SEF可以设计为 (30) 根据式(29),驱动变量子系统的状态空间方程为 (31) 其中, (32) 由式(31)可知,把A-KcE的极点配置在左半平面即可保证闭环系统的稳定性。为了简化参数调整过程,可以把极点配置在同一位置,例如 (33) 式中,ωc为控制器带宽。 控制律式(30)不仅需要系统的全状态反馈信息,而且还依赖于非线性项f,当状态反馈信息与非线性项的精确模型不完全可知时,式(30)设计的控制律便难以应用。为此,本节设计LESO用于对状态x和非线性项f进行实时观测,以获得它们的准确估计值。 由式(28)可知,总扰动f中包含高度非线性项、强耦合项。把f看作新的状态变量,并对它进行实时估计,取扩展后的状态变量xe=[x,f]T,扩展后的系统可以写作 (34) 式中:Cm=[1,0,0];ym为可测量的输出。 (35) (36) 式中:I5为5×5的单位矩阵;Lo为观测器增益矩阵。选取合适的Lo可以保证LESO能获得准确的观测值。 根据式(34),把Ae-LoCe的极点配置在左半平面,即可保证LESO的观测误差趋近于零。为了简化参数调整过程,可以把极点配置在同一位置,例如 (37) 式中,ωo为观测器带宽。 (38) 注1:式(33)和式(37)中的带宽参数ωo与ωc的取值对系统的稳定性、鲁棒性等具有重要的影响[22]。它们的优化思路为:调试出合适初值ωo,选择ωc使ωo≈(3~5)ωc;缓慢增加ωo与ωc,直到出现噪声或者震荡;然后分别增加或者减小ωo与ωc,使其满足系统指标要求。 注2:当PSLFM受到参数摄动以及输入干扰d等不确定性因素的影响时,总扰动项f中将引入新的非线性项,使f的表达式更加复杂,即式(28)改写为 (39) (40) 式中,Ao=Ae-LoCe。 令控制器误差ec=xd-x,则SEF中的误差动态可以描述为 (41) 式中,Ac=A-EKc。 联立两式得 (42) 由式(42)可知,误差动态系统的特征值是Ac和Ao的特征值,只要将控制器和观测器的极点配置左半平面,就可以确保误差动态的收敛性。假设总扰动f是有界的,存在线性扩张状态观测器以及合适的控制器参数使闭环系统是有界输入输出有界稳定的[24]。 在本章中,使用MATLAB/Simulink工具搭建仿真平台,通过对比仿真验证所提方法的有效性与优越性。 PSLFM的模型参数选取为:m=0.2,ρA=1,l=1,EI=3,Ih=0.04。考虑到系统模型的准确性和计算的难度,系统的弹性模态数取n=2。PSLFM的初始位置为x=0,y=0和目标位置x=0.877 6,y=0.479 4,相对应的初始角度为q0=0,目标角度为qd=0.5。PSO优化算法中各参数值为N=100,hmin=0.01,w=0.6,c1=2,c2=2,vmax=2,vnin=-3;ADRC控制器的带宽参数值为wc=150,wo=600。 图3 对比的仿真结果Fig.3 Simulation results of comparison 从图3(a)和图3(b)可以看到,在轨迹规划器和跟踪控制器的作用下,本文所提方法的稳定时间约为1.5 s,超调量几乎为零;而Meng等的FGAC方法超调量约为5%,稳定时间约在3.5 s。从图3(c)还可以看到,两种控制方法的弹性扰度都收敛到零的附近,都实现了振动抑制,但是本文方法更快速地实现了振动抑制。从图3(d)可以看到,控制力矩都在±1.5 N·s之间。因此本文所提方法可以降低超调量,使系统具有更好的快速性。图4(a)是f的观测值与实际值的变化曲线,图4(b)是观测误差ef的变化曲线。从图4可以看到,本文所设计的LESO实现了对非线性不确定项f的快速准确的估计。 图4 f的观测值与实际值Fig.4 The observation and the actual values of f 从图5(a)和图5(b)可以看到,系统末端点从初始角度运动到并稳定在目标角度,稳态误差与轨迹跟踪误差都很小。图5(c)显示连杆末端的残余振动逐渐收敛到零。即使系统同时受到参数摄动与外部扰动的影响,控制器也能成功抑制住柔性连杆的残余振动,实现了末端点的位置控制。图5的仿真结果验证了所提方法对输入干扰与参数摄动具有较好的鲁棒性。 图5 受不确定性影响下的仿真结果Fig.5 Simulation results under the influences of uncertainties 本文提出了一种基于PSO轨迹优化与自抗扰控制的平面欠驱动柔性机械臂振动抑制位置控制方法。该方法通过模型的欠驱动特性分析,得到了驱动变量与欠驱动变量的约束关系,并基于该关系,通过双向轨迹规划及PSO智能优化算法获得了驱动变量的最佳运动轨迹,使系统沿该轨迹到达目标位置的同时弹性振动得到抑制。基于自扰扰控制技术设计了扩展状态观测器与状态误差反馈控制律,实现了对最佳运动轨迹的精确跟踪控制。仿真与对比结果表明,所提控制方法具有超调量小、响应速度快、参数整定方便等优点,并且对输入干扰和参数摄动具有较好的鲁棒性。 值得说明的是,本文的轨迹优化是在欠驱动变量标称模型下开展的,即忽略了式(18)中的不确定性;而且ADRC控制器设计也仅考虑了驱动关节变量的不确定性因素。对于欠驱动变量模型存在不确性的情况,可以借鉴文献[25]提出的在线迭代优化算法,以对参数摄动及扰动等造成的角度偏差进行在线修正。此外,搭建实物平台以验证方法的实用性,这些将是下一步要开展的重点研究工作。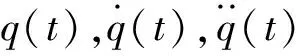
3 自抗扰轨迹跟踪控制器设计
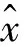
3.1 状态误差反馈控制器

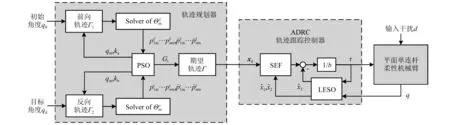


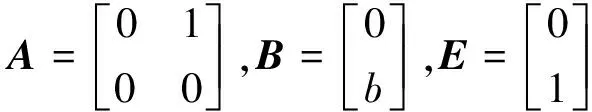
3.2 线性扩展状态观测器
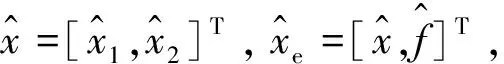

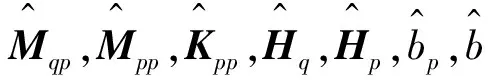
3.3 闭环稳定性
4 仿真结果与分析
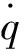

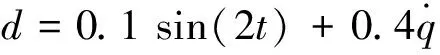

5 结 论

