排除法巧解2022年高考全国理综乙卷第16题
吴荩萱 朱建廉
(1.南京市第一中学,江苏 南京 210001;2.南京市金陵中学,江苏 南京 210005)
基于物理习题的解答,通常有两种不同的目标诉求:一是在考场环境下以“得分”为诉求的所谓“应试解答”,二是在教学情境中以“明理”为目标的所谓“教学解答”.而考场上针对业已被明示为单项选择题的试题进行解答时,如能敏锐地抓住某些“特殊数值”而切入所谓“排除法”的简单逻辑梳理,往往就可以巧妙地避开繁琐的一般性理论推演,从而达成迅捷完成试题解答过程而轻松“得分”之目标.
本文以2022年高考全国理综乙卷第16题的解答分析为例而明之.
例题.如图1所示,固定于竖直平面内的光滑大圆环上套着一个小环.小环从大圆环顶端P 点由静止开始自由下滑,在下滑过程中,小环的速率正比于
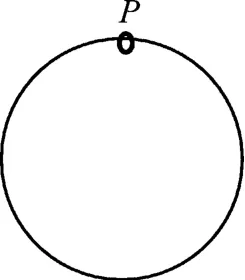
图1
(A)它滑过的弧长.
(B)它下降的高度.
(C)它到P 点的距离.
(D)它与P 点连线扫过的面积.
针对上述试题,本文给出的所谓“从某种‘特殊数值’而切入,采用‘排除法’的定性或半定量的分析”之方法,可以确保在几秒钟内便能够迅速完成试题的解答运作.相应的分析过程如下所述.
解析:如图2所示,设质量为m 的小环从大圆环的顶端P 点处由静止开始自由下滑了h 高度时获得的速率为v,于是不难根据
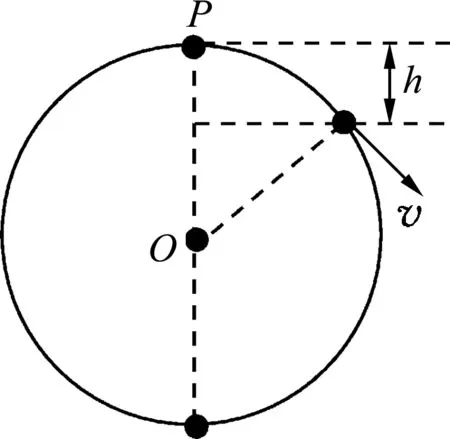
图2


表明,小环速率与它下落高度的算术平方根成正比而并非与下落高度成正比,选项(B)被排除.
如图3 所示,设大环半径为R,环心为O 点,质量为m 的小环下滑到与O点等高处时的速率为v1、下滑到大圆环底端时的速率为v2,由

图3


小环从P 点开始下滑,在获得速率v1和v2的过程中滑过的弧长分别为

表明,小环速率与滑过的弧长并不成正比,选项(A)被排除.
如图4所示,仍设大环半径为R,环心为O 点,质量为m 的小环下滑到与O点等高处时的速率为v1、下滑到大圆环底端时的速率为v2,则依然可得到v1与v2的比值仍如(1)式所给出.
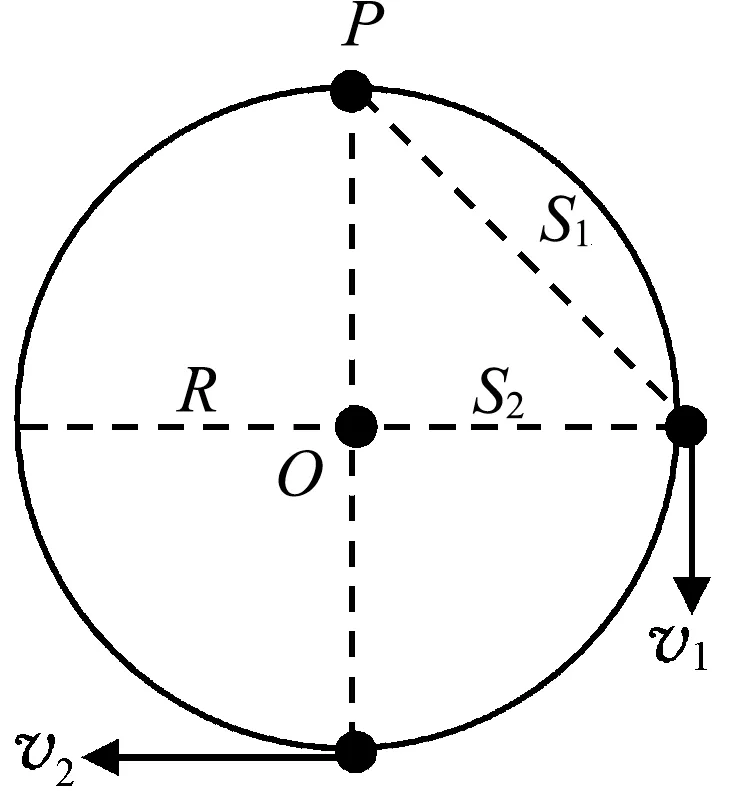
图4
但是,小环与大圆环顶点P 的连线在小环下滑过程中所扫过的面积却分别为
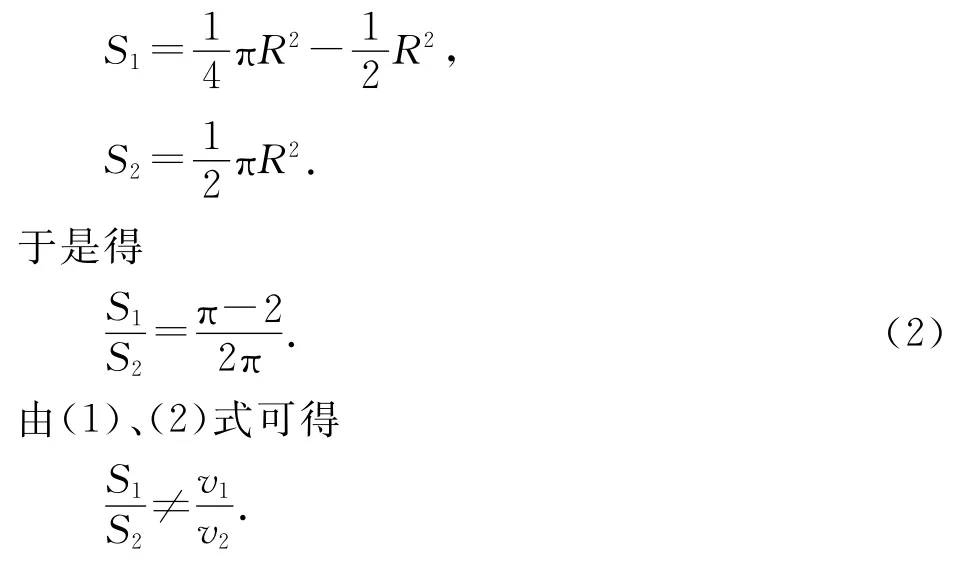
上式表明,小环速率和小环与P 点连线扫过面积不成正比,选项(D)被排除.
既然上述分析理由极其充分地依次排除了选项(A)、(B)、(D),那么我们便可以在所谓“试题命制无误”的前提下自信而做出如是之判断,即此题应选(C).
照理说,建立在上述分析基础上而给出的解答已经是基于试题“应试解答”过程的终极性判断.但是,考虑到许多教师对该试题涉及到的理论推演众说纷纭,所以本文拟把针对该试题以“得分”为诉求的“应试解答”进一步推进到以“明理”为目标的“教学解答”之中而对试题每一个选项均从不失一般性的角度切入进行理性的推演,如斯之工作在达成所谓“明理”目标的同时,还可以反衬“排除法”解答之巧妙,其具体的分析如下.
解析.如图5 所示,设大圆环半径为R,大圆环圆心为O 点,质量为m 的小环下滑了h 高度时滑过的弧长为L、与P 点相距为d、与P 点连线扫过的面积为S、与O 点连线转过的角度为θ,在如是之“不失一般性”的假设前提下,让我们理性推演而导出试题4个选项分别提及的下述关系,即速率v 与弧长L 间的函数关系v=f1(L),速率v与高度h 间的函数关系v=f2(h),速率v与距离d 间的函数关系:v=f3(d),速率v 与面积S 间的函数关系v=f4(S).
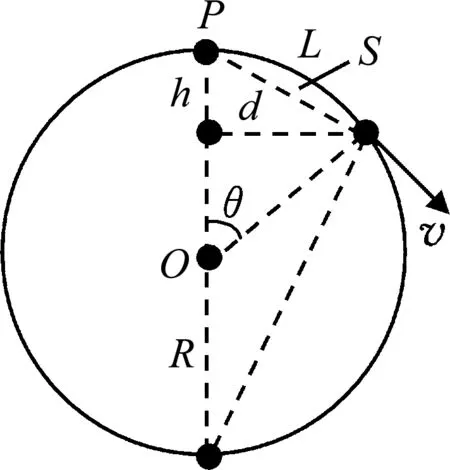
图5
解析:由机械能守恒和图5 所示的几何关系可得
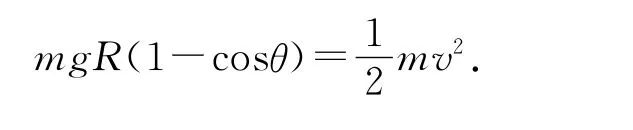

看上去,由(4)式给出的“S 表示为θ 的函数”而获取其反函数后代入(3)式便可完成所谓“速率v与面积S 间函数关系”的构建,但是形如(4)式所示之超越函数的反函数无法给出显性表达,所以我们只能做出如下判断.
小环下滑获得的速率与小环和P 的连线扫过面积间的一般性函数关系只能隐性存在而不能给出显性表达,而这种隐性存在的函数显然不可能是正比例函数.
在结束本文之际想强调指出:针对被明示为单项选择题型的试题在考场的环境中作所谓以“得分”为目标诉求的“应试解答”时,从某种“特殊数值”切入到“排除法”所对应的逻辑梳理过程,从而避开不失一般性的繁杂理性推演,显然是一种上佳的选择.

