四足机器人足端复合轨迹的优化与性能分析*

魏顺祥，吴海波，陈久朋，刘亮，熊彬州，徐洋洋

1. 昆明理工大学机电工程学院，云南 昆明 650500

2. 珠海华冠科技股份有限公司，广东 珠海 519000

仿生机器人是当前研究的热点问题，而良好的足端轨迹可以增加四足机器人对复杂地形的适应性和稳定性，因此四足机器人的轨迹规划是研究的重要问题［1-3］。四足机器人的轨迹规划通常是在笛卡尔空间或关节空间中进行的，并且两者之间存在着映射关系。笛卡尔空间轨迹规划能直观了解足端的运动轨迹，但求解关节转角的逆运动学计算量很大。关节空间轨迹规划常采用插值的方法，在运算方面有着较好的优越性［4-5］。常见的足端轨迹有摆线轨迹和多项式轨迹等方式［6-8］。Yoshihiro Sakakibara 等提出了摆线轨迹的规划方法［9］。王立鹏等提出了足端零冲击轨迹，使足端轨迹在理论上具有零冲击的特性［10］。袁帅东等改进了摆线轨迹，在摆动相中间加了一条水平线，增强了足端的跨障能力［11］。为了使加速度连续并得到更平滑的足端轨迹曲线，Thomas Buschmann提出了基于分段五次多项式的足端轨迹［12］，该轨迹可在保证加速度曲线连续的同时，保证足端在起落点时实现理论上的零冲击。邓华等利用五次多项式对六足并联机器人的足端轨迹进行规划，取得了良好的效果［13］。周坤等利用五次多项式规划了摆动腿跨步阶段的足端轨迹，并在四足机器人上进行了实验验证［14］。常用的关节空间轨迹规划方法有线性插值、B样条插值法和高阶多项式插值等［15］。线性插值法简单方便，但其速度不连续且要求加速度无限大。高阶多项式可保证关节空间运动过程中的角速度和角加速度连续。Reza Dehghani 等使用五次多项式插值进行了五连杆两足动物的循环步态规划和运动控制［16］。仲军等根据主动力矩最小的原则，使用八阶多项式对四足机器人关节空间进行了轨迹规划和实验验证［17］。

理想情况下，可通过无限细分足端轨迹点数量进行逆解来计算关节角度，从而获得关节运动的特性曲线来控制关节的精确运动。但由于控制器计算能力的限制，无法进行密集取点并进行运动学逆解计算。本文将笛卡尔空间和关节空间规划的优点相结合，对规划好的足端轨迹进行离散采样，使用不同的插值点选取方式确定较少的插值点位置进行运动学反解；并在关节空间内进行角速度和角加速的优化，再对相邻的插补点之间用五次多项式函数关系进行连接［18］，以获得平滑的关节曲线来驱动电机运动。因只需对足端轨迹曲线的采样点进行逆运动学计算，本文的方法极大地减少了计算量。最后，将得到的足端轨迹与理想的足端轨迹进行了误差比较，得到了最优的插值方法和角速度、角加速度优化方法。

1 足端轨迹规划

1.1 轨迹规划

摆线运动规律因能很好地满足足端零冲击的轨迹规划要求，在四足机器人的足端轨迹规划中得到了广泛的应用，其表达式为

式中H为抬腿高度，S为步幅，Tf为摆动相周期，Tω为摆动相周期的一半。

文献［12］中，Thomas Buschmann 基于五次多项式构造足端轨迹，使得该轨迹具备足端零冲击以及速度、加速度连续的特点。相比于摆线运动规律，基于五次多项式构造足端轨迹无泰勒级数展开求解的负担。其数学表达式为

基于摆线类型的轨迹具备圆弧形的特点，方便在后续使用切比雪夫点进行插值点的选取；而基于五次多项式类型的轨迹，在后续进行五次多项式关节空间轨迹规划中具有连贯性和一致性。因此，本文选用了摆线轨迹X方向的曲线和五次多项式轨迹Y方向的曲线，建立了复合足端轨迹（以下简称复合轨迹），实现了将摆线运动规律和五次多项式运动规律的融合。该轨迹曲线既结合了摆线规律和五次多项式规律的优点，又使得足端在理论上具有零冲击、速度和加速度连续的特点，其形式为

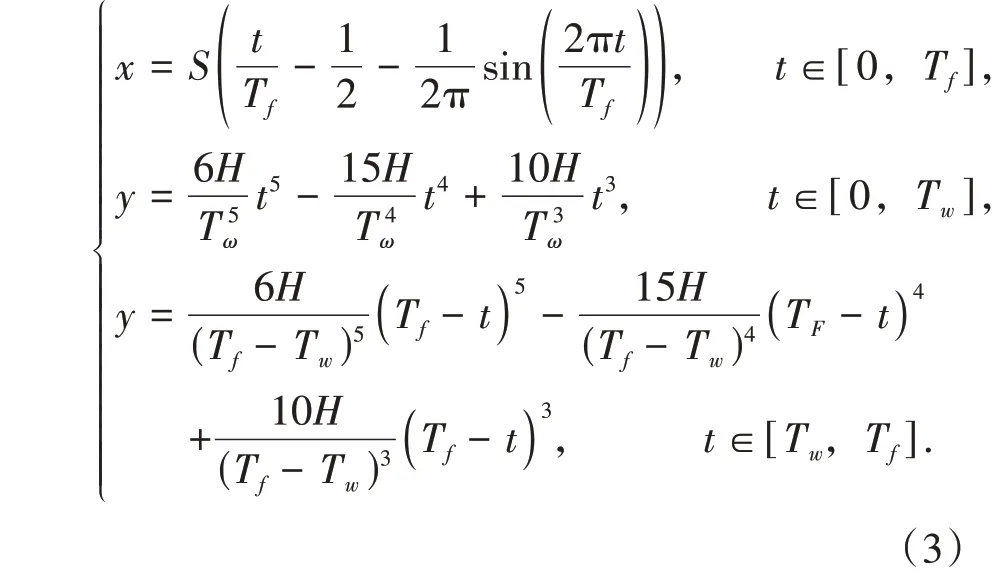
给出一组运动参数H= 40 mm，S= 160 mm，Tf= 0.5 s，Tw= 0.25 s。图1 是根据给定参数得出的笛卡尔坐标空间的三类足端轨迹曲线。其中，复合轨迹具有更大的底部运动空间，落地角度更加垂直不易打滑，故选取复合轨迹作为四足机器人的足端轨迹。

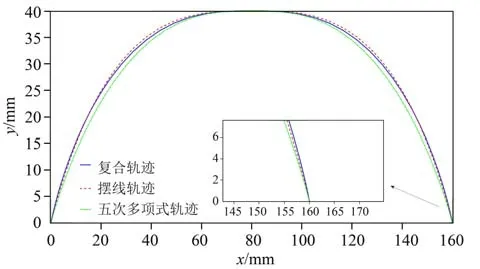
图1 笛卡尔坐标空间的三类足端轨迹Fig.1 Three types of foot trajectories in Cartesian coordinate space

1.2 机构描述及运动学分析

为了便于进行轨迹规划研究，采用简化模型进行运动学分析。如图2所示，整机采用前肘后膝式配置。设大腿长为L1，小腿长为L2，髋关节转角为θ1，膝关节转角为θ2。

图2 四足机器人简化模型Fig.2 Simplified model of a quadruped robot

用Simulink 搭建上述简化模型的单腿运动系统。通过对该系统发送一个时间信号激励，使该模型按照设定的复合轨迹进行逆向运动学求解，并通过求解的结果驱动系统的物理模型进行轨迹的运动学仿真。取L1= 170 mm，L2= 255 mm，单腿一个步态周期的连杆结构轨迹如图3所示。

图3 单腿一个步态周期的连杆结构轨迹Fig.3 A gait cycle link structure trajectory of a single leg

在Simulink仿真中，获得髋膝关节的位移、角速度和角加速度如图4 所示。图4 中，关节转动的角度曲线平滑无突变，角速度、角加速度曲线在较小范围内平缓波动。上述关节运动曲线是微分细化后的求解结果，是对理想的关节运动曲线的逼近［19］。但在实际使用中，由于控制器计算能力有限，无法拾取大量中间点并进行运动学正反解计算，这将极大阻碍系统运动的实时性［20］。同时，微分的过程忽略了各个相邻中间点之间的连接关系，仅是对求解后的点进行直线对接，会导致与实际运动情况不符［21-22］。

图4 髋膝关节的位移、速度和加速度曲线Fig.4 Displacement,velocity and acceleration curves of hip and knee joint

2 关节空间轨迹优化

2.1 插值点的选取

合适的插值点选择可以将轨迹的中间点数量降到最少，增加轨迹与理想轨迹的接近程度。对足端轨迹进行离散插值的方法有等间距点、等时点及切比雪夫点等多种方法［23-24］。在轨迹平面内，对x方向等分称为等间距点；对时间t等分称为等时点；切比雪夫点是单位圆周上等距分布的横坐标，在端点处更密集，更适合于圆弧曲线的插值。由于切比雪夫点可避免龙格现象的产生，因此被广泛地用于高阶多项式的插值。第二类切比雪夫多项式为

其中n∈N，x∈R，且|x| ≤1。式（4）也可记为

这里n∈N，x∈C。对式（5）求根，即可得第二类切比雪夫点。n阶第二类切比雪夫多项式在区间[-1，1]内有n+ 1个根，即

其中k= 0，1，2，…，n。在轨迹上选取11 个插值点将曲线分为10 份，表1 给出了等间距插值点、切比雪夫插值点以及等时插值点的坐标值，与图5中轨迹曲线上的插值点对应。

表1 三种足端插值点位置Table 1 Three kinds of foot-end interpolation point position

图5 三种足端插值曲线Fig.5 Three kinds of foot-end interpolation curves

2.2 五次多项式插补

为了确定三种插值对关节空间映射效果，将等间距点、切比雪夫点和等时点对应的轨迹点作为选用的插值映射点进行运动学反解求得关节空间的轨迹插值点。这在很大程度上减轻了控制器的计算负担，增强了系统运动的控制实时性。为保证各插值点之间平滑过渡，以达到相邻点之间的角度、角速度、角加速度值连续的效果，需要在各相邻插值点之间设置插补函数。五次多项式能满足角度θ，角速度ω，角加速度α连续的最少阶数要求，相比于更高阶的多项式，计算量较小，还能够避免龙格现象。所以，本文采用五次多项式曲线对各相邻插值点进行连接，通过确定各插值点的关节特性参数，从而保证两个插值点之间的平滑性。五次多次式的一般表达式为

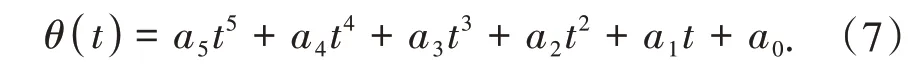
给定边界条件为

其中θ0，ω0，α0为起始点的角度、角速度和角加速度。θf，ωf，αf为终止点的角度、角速度和角加速度。将边界条件代入（7），得

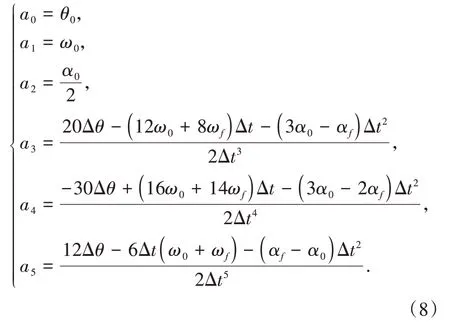
一般情况而言，式（8）中的θ0，θf是已知的，ω0，ωf，α0，αf可通过差商来确定。然而，差商的结果与实际偏差较大，所以本文构造Hermite多项式估计关节插值点的角速度和角加速度，从而减少关节的冲击和振动，提升机器人关节空间运动轨迹的平滑性。

首先，取前3 个插补点θ1，θ2，θ3和边界条件ω1= 0 来构造三次三节点的Hermite 多项式，即多项式P(t)满足条件

因此，Hermite多项式为

其中

第二个插值点的角速度和角加速度估计值为ω2，α2。同理，ωi，αi可以由θi-1，θi，θi+1和已经求出的ωi-1来确定，其中i= 2，3，…，9。从而，求出除首末两点之外的所有插值点的角速度和角加速 度。 设 定ω与α的 首 末 边 界 条 件 为ω1= 0，ω11= 0，α1= 0，α11= 0，就可得到全部关节插补点的角度、角速度、角加速度数据。

在给定插值点基础上进行逆向运动学求解，得到11 个关节空间插值点，分别对三类插值点构造三次三节点的Hermite 多项式来估计插值点的角速度和角加速度，并对其进行五次多项式轨迹规划。图6是采用切比雪夫点插值轨迹获得的关节角速度、角加速度和角加加速度。可以看出，采用Hermite 多项式估计方法能有效的减少角加速度和角加加速度的突变值大小，角速度曲线也变得更加的平滑。

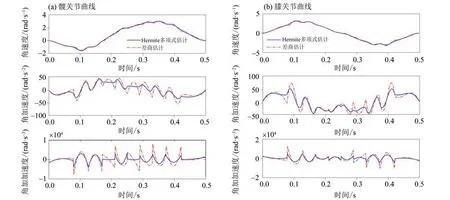
图6 关节角速度、角加速度和角加加速度的对比分析Fig.6 Comparative analysis of joint angular velocity,angular acceleration and angular jerk

表2 和3 分别为对三类插值点使用Hermite 多项式和差商估计得到的角加速度、角加加速度突变最大值以及角加速度、角加加速度减少率。以髋关节为例，等间距插值点角加速度减少率为38.93%，切比雪夫插值点角加速度减少率为20.53%，等时插值点角加速度减少率为7.83%。所以，三类插值点情形下，采用Hermite 多项式估计方法对髋膝关节角加速度和角加加速度的突变最大值均有较大的减小。

表2 三类插值点的Hermite多项式和差商估计角加速度突变最大值、减少率Table 2 The Hermite polynomial and difference quotient estimation of three types of interpolation points to estimate the maximum angular acceleration abrupt change and reduction rate

此外，采用等时插值和Hermite 多项式估计方法的髋膝关节角加速度突变最大值分别为41.38和45.86 rad/s2。在3 种插值方法中，等时插值的角加速度突变最大值最小；虽然切比雪夫插值的角加加速度突变最大值最小，但和等时点插值差别不大。且角加速度对于运动的影响更大，因此使用等时插值和Hermite 多项式估计方法有利于减少电机的抖动和控制器的功耗。

3 仿真与实验

3.1 单腿轨迹仿真与实验

为了验证实际应用效果，使用实验室开发的四足机器人。图7是简化单腿与实际腿部之间的映射关系。根据几何关系可知，四足机器人实际结构和简化结构之间存在转换关系

图7 单腿映射关系Fig.7 Single-leg mapping

采用Simulink 对该机器人进行运动仿真分析，图8是单腿摆动相的虚拟样机运动过程。为了定量描述实际曲线和理想复合曲线的偏差大小，这里采用式（14）计算平均误差值（以下简称为误差值），即

图8 虚拟样机的运动过程Fig.8 The movement process of the virtual prototype

式中n代表实际曲线和理想复合曲线的取点个数，(̑(ti)，̑(ti))为实际曲线上的点，(x(ti)，y(ti))为理想曲线上的点。

在实际曲线和理想的复合轨迹曲线上，各取500 个点用式（14）进行误差计算，结果如表4 所示。可以看出，等时点插值的曲线与理想的复合轨迹的接近程度更好，Hermite 多项式估计方法相比于差商估计对曲线的接近程度有明显的提高；使用Hermite 多项式估计，等距点插值的误差降低了12.61%，切比雪夫点插值的误差降低了23.3%，等时点插值误差降低了29.24%。

表4 两种插值法的曲线误差比较Table 4 Comparison of the curve error of the two interpolation methods

表3 三类插值点的Hermite多项式和差商估计角加加速度突变最大值、减少率Table 3 The Hermite polynomial and difference quotient estimation of three types of interpolation points to estimate the maximum angular jerk abrupt change and reduction rate

图9 是实体样机使用Hermite 多项式估计的等时点插值方法在一个摆动相运动周期内的运动过程。通过激光跟踪仪来对足端进行跟踪采集来获得实际样机的足端轨迹，如图10 所示。由于实际样机腿部关节处存在装配间隙，导致激光跟踪仪采集得到的足端轨迹和仿真得到的足端轨迹存在细小的偏差。但通过实体样机实验，可以看出机器人单腿运动平稳，无明显抖动现象，证明了所提出算法的有效性和正确性。

图9 实体样机的运动过程Fig.9 The movement process of the physical prototype

图10 激光跟踪仪获得的实际样机足端轨迹Fig.10 Foot trajectory of actual prototype obtained by laser tracker

3.2 步态仿真实验

为了验证复合轨迹在四足机器人上的行走的效果，使用Matlab和Adams进行联合仿真实验。采用trot步态，设定步态周期为0.8 s，使用本文所提出的复合轨迹和优化算法进行四足机器人整机的步态仿真。四足机器人一个步态周期的运动如图11所示。

图11 四足机器人一个步态周期运动Fig.11 A gait cycle of a quadruped robot

在仿真模型上应用复合轨迹、摆线轨迹和五次多项式轨迹进行tort步态仿真实验。躯干质心在世界坐标系上运动轨迹如图12～13 所示。图12 中，三种轨迹的四足机器人步态平稳，无明显打滑现象；且由放大图可以看出，复合轨迹质心位移最远，其速度为395.17 mm/s，更不易发生打滑。图13 中，三种轨迹的四足机器人运动平稳，躯干的起伏波动较小，且应用三种轨迹的机器人质心波动范围差别很小。以上证明了所设计的复合轨迹和相关算法的可行性。

图12 躯干质心在前进方向上的运动轨迹Fig.12 The trajectory of the torso center of mass in the forward direction

图13 躯干质心在竖直方向上的运动轨迹Fig.13 The trajectory of the torso center of mass in the vertical direction

4 结 论

针对四足机器人的笛卡尔空间足端轨迹规划，研究了摆线运动规律和五次多项式运动规律的性质和特点，将两者相结合得到了一种复合足端轨迹。为降低实际运动过程中足端轨迹的运动学计算负担，将复合足端轨迹的插值点数量压缩至11个，同时采取等间距点、切比雪夫点和等时点三类插值点来进行比较分析。

利用五次多项式曲线对各插值点之间进行关节空间轨迹规划，使用Hermite 多项式曲线进行对插值点的角速度和角加速度估计，得到了基于三类插值方法的关节空间运动曲线。结果表明：使用Hermite 多项式估计的关节空间各关节的角速度变化更加平滑，角加速度和角加加速度的突变值明显减少。对三类插值方法而言，等时点插值的角加速度突变值更低，效果更好。

通过Simulink 进行单腿仿真，并使用Hermite多项式估计，所得到的足端实际轨迹与理想的复合轨迹的误差值明显减少。采用等时点进行插值的方法所得到的实际轨迹与理想的复合足端轨迹更为接近。通过实体样机实验和整机的步态仿真实验，验证了上述方法和结论的有效性和正确性。