形式下三角矩阵环上的n-Ding模*

张文汇，刘婷

西北师范大学数学与统计学院，甘肃 兰州 730070

20世纪90年代，Enochs等［1-2］引入了Gorenstein投（内）射模和Gorenstein平坦模，这三类模及其维数理论构成了Gorenstein 同调代数的理论核心。近年来，随着Gorenstein 同调理论的进一步丰富发展，出现了许多有重要理论意义的研究成果。2009年，丁南庆和毛立新先后引入GorensteinFP-内射模和强Gorenstein平坦模，这分别是特殊的Gorenstein 内射模和Gorenstein 投射模［3-4］。之后，Gillespie 将这两类模重新命名为Ding 投射模和Ding 内射模［5］。2015 年，唐曦在交换的Noether 环上引入了n-Gorenstein 投射模和n-Gorenstein内射模的概念，并且研究了这两类模的同调性质［6］。

本文所提到的环均指有单位元的非零结合环，模均指酉模。

受以上文献的启发，我们讨论形式下三角矩阵环上n-Ding 模的刻画及其同调性质。称左R-模M是Ding 投射模，如果存在投射模的正合列P：… →P1→P0→P-1→P-2→…，使得M≅Im(P0→P-1)，且对任意平坦左R-模F，序列HomR(P，F)正合；称左R-模E是FP-内射模，如果对任意有限表示左R-模H，ExtR1(H，E) = 0；称左R-模N是Ding 内射模，如果存在内射模的正合列ℑ：… →I1→I0→I-1→I-2→…，使得N≅Im(I0→I-1)，且对任意FP-内射左R-模E，序列HomR(E，ℑ)正合。对于环R，用LM(R)（RM(R)）表示左（右）R-模范畴，RM(MR)表示左（右）R-模M，用pdM(fdM，FP-idM)表示R-模M的投射（平坦，FP-内射）维数。模M的示性模M+= HomZ(M，Q/Z)，Z 表示整数集，Hi(X) 表示复形X的第i次同调群。

定义范畴LM(A) 和LM(B) 的积LM(A) × LM(B) 是如下范畴：其对象为有序对(M，N)，其中M∈LM(A)，N∈LM(B). 任取LM(A) × LM(B) 中的对象(M，N) 和(M′，N′)，态射集

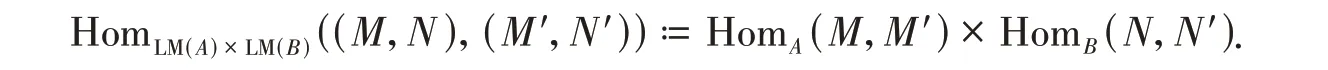
对任意态射(f，g)：(M，N) →(M′，N′)和(f′，g′)：(M′，N′) →(M″，N″)，态射的合成为(f′，g′)(f，g)：=(f′f，g′g).

以下是我们要用到的范畴LM(T) 与LM(A) × LM(B) 之间的几个函子：

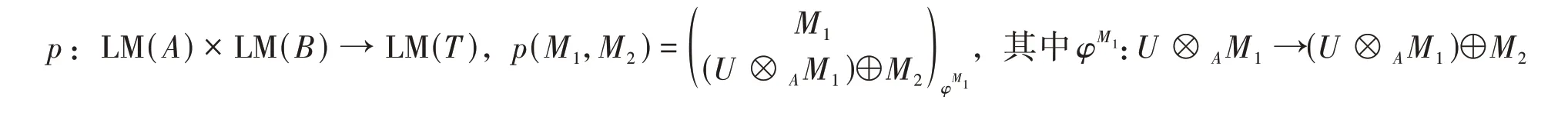
定义q：LM(T) →LM(A) × LM(B)为

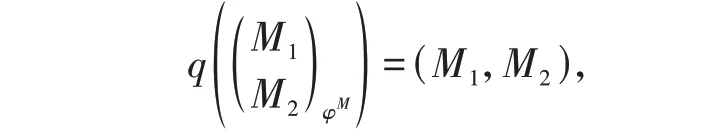
且对LM(T)中的任意态射有

因此(p，q)，(q，h)均为伴随对，从而q是正合函子，p保持投射对象，h保持内射对象[10]。

1 n-Ding投射模

下面讨论形式下三角矩阵环T上n-Ding 投射模的相关性质。

证明 （i）存在投射左T-模的正合列

由引理1可得投射左A-模的正合列

其中M1≅Im. 任取平坦左A-模F，则存在左T-模的正合列

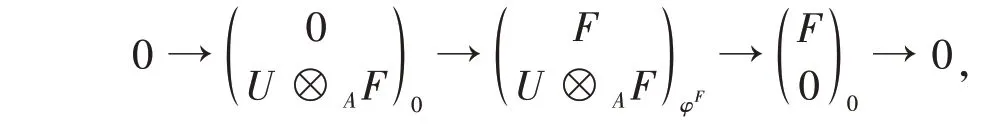
其中φF：U⊗AF→U⊗AF是同构。因此可诱导复形的短正合列

因为fdUA＜+∞，由文献［10］的引理2.3 可知序列U⊗AΔ1正合，所以图中1 ⊗λ1是单同态。再由引理1知，φ-1是单同态，故φM是单同态。

由第一列和第二列的正合性及长正合序列引理，可得投射左B-模的正合列

对任意m∈Z，由函子p，q的伴随性，得

（ii）因为φM：U⊗AM1→M2是单同态，所以存在左T-模的正合列

其中φM1：U⊗AM1→U⊗AM1是同构。又因为M1是n-Ding 投射左A-模，所以存在投射左A-模的正合列

使得M1≅Imf0，且对任意平坦左A-模F，任意整数i≥-n，Hi(HomA(Λ，F)) = 0. 因为fdUA＜+∞，所以序列U⊗AΛ 正合，因此可得投射左T-模的正合列

因为左B-模M2/ImφM是n-Ding 投射模，所以存在投射模的正合列

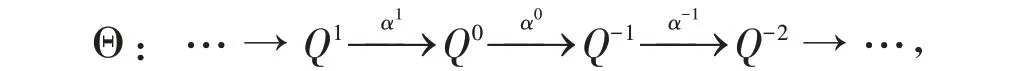
使得M2/ImφM≅Imα0，且对任意平坦左B-模G， 任意整数i≥-n，Hi(HomB(Θ，G)) = 0. 因此可得投射左T-模的正合列

2 n-Ding内射模

设Γ 是 一 范 畴， 其 对 象 是 三 元 组W=(W1，W2)φW， 其 中W1∈RM(A)，W2∈RM(B) 且φW：W2⊗BU→W1是 右A-模 同 态。任 意 两 个 对 象(W1，W2)φW与(X1，X2)φX间 的 态 射 是g=(g1，g2)，其 中g1∈HomA(W1，X1)，g2∈HomB(W2，X2)，且满足φX(g2⊗1) =g1φW. 范畴RM(T)与范畴Γ 等价[15]。我们仍以三元组(W1，W2)φW的形式表示右T-模。注意到，g是单（满）同态当且仅当g1和g2是单（满）同态。设W=(W1，W2)φW是右T-模，由伴随同构HomA(W2⊗BU，W1)≅HomB(W2，HomA(U，W1)). 任取w∈W2，u∈U，定 义：W2→HomA(U，W1) 的 作 用 为(w)(u) =φW(w⊗u)， 则是 右B- 模 同 态。 设g=(g1，g2)：(W1，W2)φW→(X1，X2)φX，

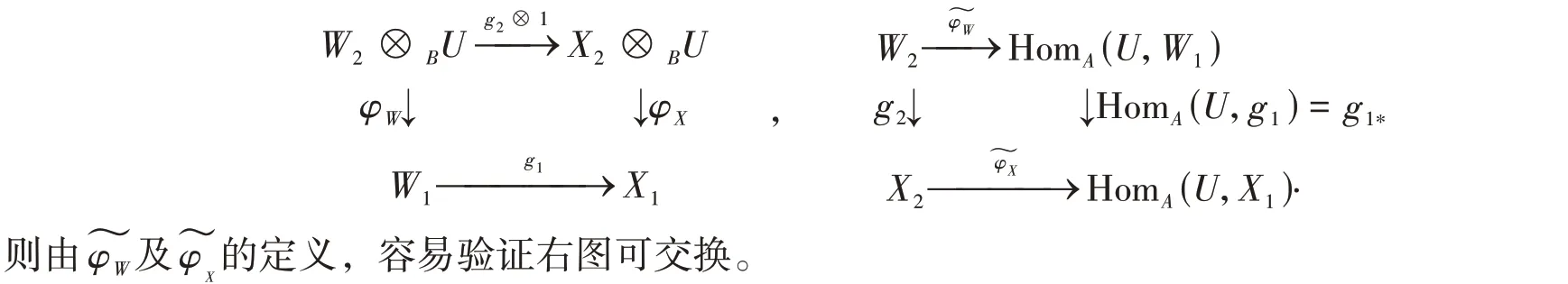
类似地，可以定义范畴RM(A) 和RM(B) 的积，即范畴RM(A) × RM(B)以及范畴RM(T)与RM(A) ×RM(B)之间的几个函子：

p：RM(A) × RM(B) →RM(T)，p(W1，W2)=((W2⊗BU)⊕W1，W2)φW，其 中φW：W2⊗BU→(W2⊗BU)⊕W1的标准单射；对任意态射(g1，g2)，p(g1，g2)=((g2⊗B1)⊕g1，g2).

q：RM(T) →RM(A) × RM(B)，对 任 意 右T-模W=(W1，W2)φW，q((W1，W2)φW)= (W1，W2)，且 对 范 畴RM(T)中的任意态射(g1，g2)，q((g1，g2)) =(g1，g2).

则(p，q)，(q，h)均为伴随对，从而q是正合函子，p保持投射对象，h保持内射对象[11]。

定义2[13]设n是一固定的正整数。称右R-模N是n-Ding内射模，如果存在内射模的正合列

使得N≅Im(I0→I-1)，对任意FP-内射右R-模E，任意整数i≥-n，Hi(HomR(E，Ι)) = 0.

称环R是右凝聚环，如果每个有限生成右理想都有限表示。下面我们讨论形式下三角矩阵环T上n-Ding内射模的结构。

引理3[11]设W=(W1，W2)φW是一右T-模。

（i）W是内射模当且仅当W1是内射右A-模，Ker是内射右B-模，且是满同态；

（ii） 若T是右凝聚环，UA是有限表示模，则W是FP-内射模当且仅当W1是FP-内射右A-模，Ker是FP-内射右B-模，且是满同态。

命题1 设T是右凝聚环，UA是有限表示模，且fdBU＜+∞. 若J是FP-内射右A-模，则右T-模(J，0)0的FP-内射维数有限。

证明 不妨设fdBU=m＜+∞. 由右T-模的序列

的正合性，可诱导出左T-模的正合列

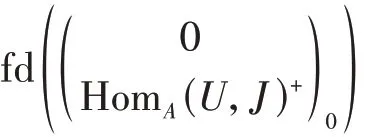
定理2 设T是右凝聚环，BU是平坦模，UA是有限表示模且其投射维数有限，W=(W1，W2)φW是右T-模。

（i） 若W是n-Ding内射模，则W1是(n- 1)-Ding内射右A-模，是满同态，且Ker是n-Ding内射右B-模；

（ii） 若W1是n-Ding 内射右A-模，是满同态，且Ker是n-Ding 内射右B-模，则W是n-Ding 内射模。

证明 （i）存在内射右T-模的正合列

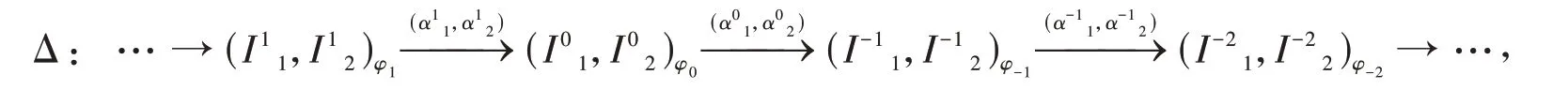
使得W≅Im(，)，且对任意FP-内射右T-模E=(E1，E2)φE，任意整数i≥-n，Hi(HomT(E，Δ))= 0. 由引理3可得内射右A-模的正合列

其中W1≅Im. 任取FP-内射右A-模J，则右T-模的序列

正合，且对任意f∈HomA(U，J)，u∈U，φJ(f⊗u) =f(u)，从而是同构。于是得到复形的短正合列

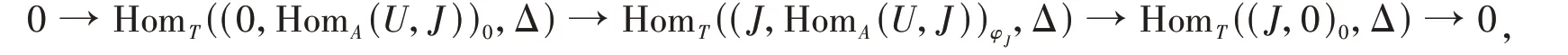
由 引 理3 可 知， (J，HomA(U，J))φJ是FP- 内 射 右T- 模， 故 对 任 意 整 数i≥-n，Hi(HomT((J，HomA(U，J))φJ，Δ)) = 0. 因为BU是平坦模，由文献［11］的引理4.2 可知，HomA(U，J)是FP-内射右B-模，故(0，HomA(U，J))0是FP-内射右T-模，因此对任意整数i≥-n，Hi(HomT((0，HomA(U，J))0，Δ)) =0. 利用长正合序列引理可知，对任意整数i≥-n+ 1，Hi(HomT((J，0)0，Δ)) = 0. 对任意m∈Z，由

故对任意整数i≥-n+ 1，Hi(HomT((J，0)0，Δ)) ≅Hi(HomA(J，Δ1)) = 0，因此W1是(n- 1)-Ding 内 射 右A-模。

设(π1，π2)：(，)φ0→W是序列Δ中的满同态，考虑如下交换图。

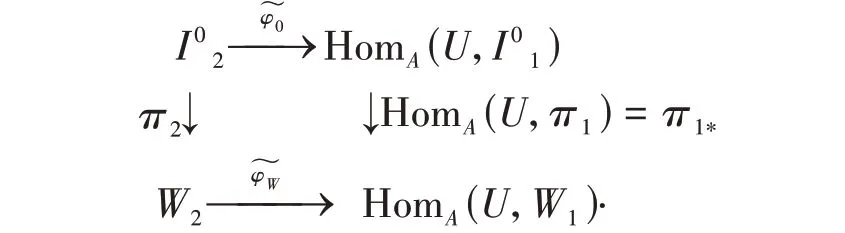
因为pdUA＜+∞，所以由文献［10］的引理2.5 可知，序列HomA(U，Δ1)正合，故π1*是满同态。又因为(，)φ0是内射右T-模，所以由引理3可知是满同态。因此是满同态。

对任意j∈Z，存在态射ρj：Ker→Ker，使得行正合的下图可交换。

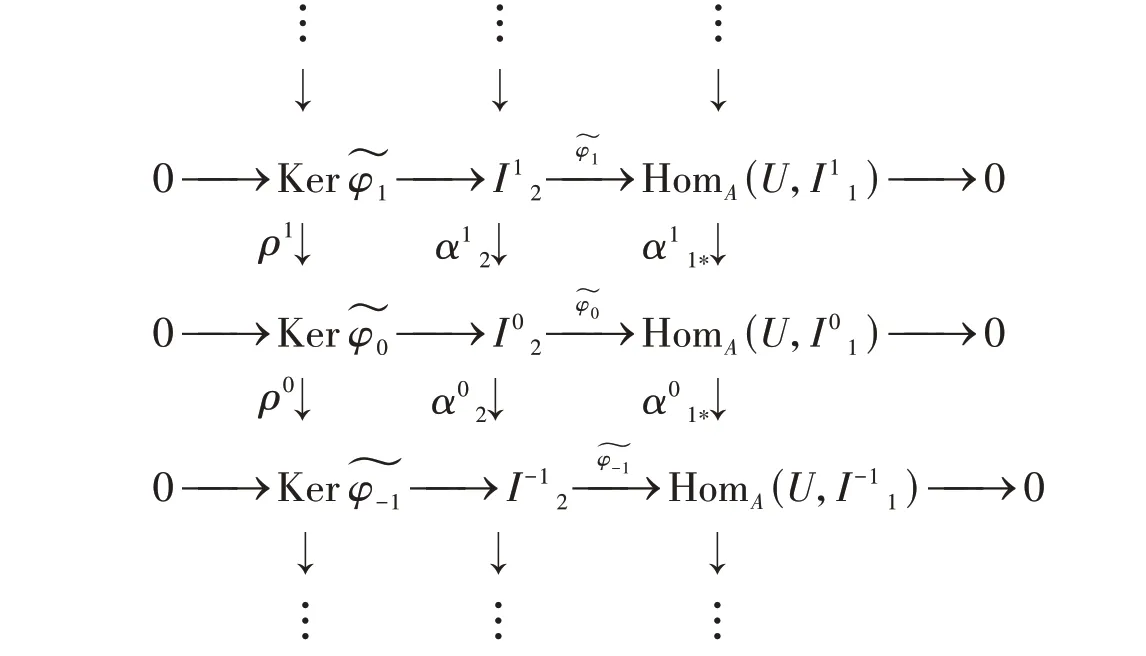
由第二列和第三列的正合性及长正合序列引理，可得内射右B-模的正合列

综上，再由文献［13］的命题2.3可知在正合列(*)中，右T-模W=(W1，W2)φW是n-Ding内射模。

推论2 设R是右凝聚环，T=是由R作成的形式下三角矩阵环，W=(W1，W2)φW是一右T-模。

（i） 若W是n-Ding 内射模，则W1是(n- 1)-Ding 内射右R-模，是满同态，且Ker是n-Ding 内射右R-模；

（ii） 若W1，Ker是n-Ding 内射右R-模，是满同态，则W是n-Ding 内射右T-模。

证明 由文献［16］的推论4.5可知T是右凝聚环，再由定理2易见结论成立。