“错位相减法”求和问题的另一突破路径探讨

蒋彦磊

（南京市江宁高级中学，江苏 南京 211100）

数列求和问题一直是高考中一类比较常见的题型，是高考中的热点与重点之一。对于“等差*等比”型的数列求和，传统的方法是“错位相减法”，该方法虽操作过程简单，但式子变形技巧强、关键点多、对学生的运算能力要求高等，学生经常不小心就出错。本文笔者从另一视角探究解决此类型数列求和的其他一般性解法，供大家参考。

一、问题的提出

数列是高考考查的重点内容，主要考查学生的运算求解能力，无论是小题还是解答题都有所涉及，尤其是数列求和问题涉及的知识点多、方法多、综合性强等对学生的能力要求高，很多学生常因解答过程繁杂、运算能力弱导致失分。若能转换因方法多样、题型灵活问题解决的视角，认清本质也可以简化运算，提高解题效率。以下面问题为例：

（2020 全国3 理17）设数列{an}满足a1=3,an+1=3an-4n。

（1）略；（2）求数列｛2n·an｝的前n项和Sn。

此题，第（1）问是典型的构造数列求通项问题，根据递推式的结构特点，考虑到两边加上一个等差数列的相邻项即可构造特殊数列｛an-2n-1｝为常数列，从而得an=2n+1。第（2）问是数列求和问题，通项公式为“等差*等比”型，通常利用错位相减法可以得出结果Sn=(2n-1)·2n+1+2。但通过以往的教学可以知道，错位相减法容易理解，且操作过程固定，学生易于掌握，但因计算量大，注意点多，学生经常出错，有些老师也会错误地引导，认为解决此类数列求和的方法只有这一种，让学生遇到此类问题总有一种“自古华山一条道”感觉，战战兢兢地算下去。但数列的本质特点是按照一定次序排成的一列数，项与和之间本质上可以直接转化，所以，对于问题（2）是不是可以借助项和关系可参考问题（1）的方法构造新数列解决呢？

二、问题的解决

由项和关系式易知：当n≥ 2时即观察：数列｛(2n+1)·2n｝是由等差数列｛(2n+1)｝与等比数列｛2n｝相乘构造，可尝试把数列｛(2n+1)·2n｝拆分成两个相同结构的一个数列的相邻两项的差，再直接构造与Sn有关的新数列，间接得到Sn。

（一）尝试构造，解决问题

解：（1）an=2n+1；

利用待定系数法，令

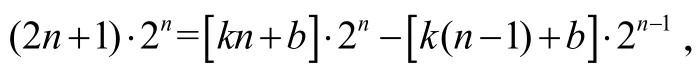
对应系数相等得k=4,b=-2.

所以，(2n+1)·2n=(4n-2)·2n-(4n-6)·2n-1,n≥2.

记bn=(4n-2)·2n.则 (2n+1)·2n=bn-bn-1,n∈N*且n≥2.

所以，Sn=Sn-1+bn-bn-1,n≥ 2.即Sn-bn=Sn-1-bn-1,n≥2.

又当n=2时，S2-b2=S1-b1=2.

所以数列｛Sn-bn｝为常数列，即Sn-bn=2,n∈N*.所以，

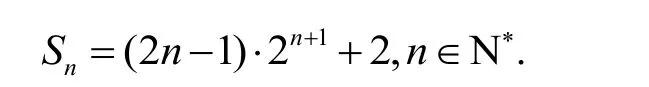
（二）优化解法，发现本质

在前面，构造关于与Sn有关的新数列的过程中，得到Sn=Sn-1+bn-bn-1,n≥ 2.即

Sn-Sn-1=bn-bn-1,n≥ 2.所以，求和过程还可以做“裂项”处理：

（接方法 一）因为bn=(4n-2)·2n，则(2n+1)·2n=bn-bn-1,n∈N*且n≥ 2.又 当n=0,1时也成立。所以

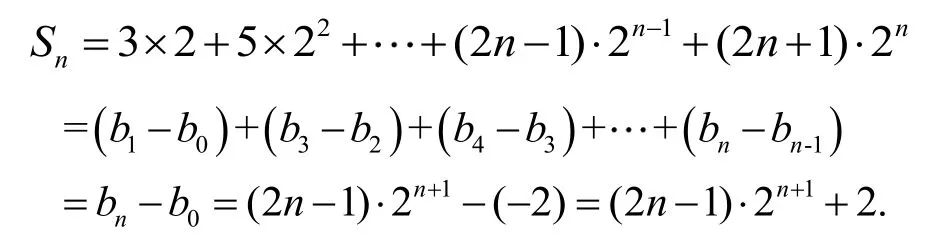
其实上述解决问题的两个角度是有必然联系的，都可以归为裂项变形策略，下统称为“裂项法”。由于数列通项的特点是等差数列*等比数列，考虑到等差数列通项公式的特点及推导方法（裂项叠加消元），也可把通项变形为有相似结构的数列相邻两项的差，如：［a(n+1)+b］·qn+1-（an+b）·qn，再利用待定系数法确定系数，就可以顺利将错位相加法求和问题转化为裂项相消解决，大大减少了运算难度，且不容易出错。只是在确定系数时要细心计算，对求得的检验一下，确保无误再继续求和。该方法更接近问题的本质，相比于“错位相减法”的计算过程，运算过程更优化，学生更容易算对，这不仅能提升学生学好数学的信心，拓宽了学生的思维，也提醒老师在日常教学中引导学生多视角思考问题，多角度解决问题。同时也给老师的教学研究提供了新的思考点，更有利于培养学生的数学核心素养和关键能力。

三、问题的引申

（一）结论

一般模型数列{(an+b)·qn}其中a≠0,q≠0 且q≠1 的前n项和为Sn，则

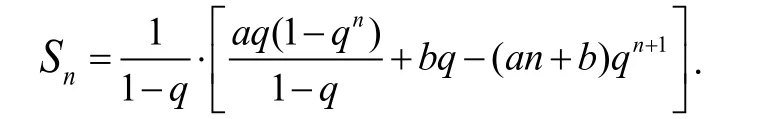
证明：

记数列｛（an+b）·qn｝其中a≠ 0,q≠ 0且q≠ 1的前n项的和为Sn。由错位相减法可以得到

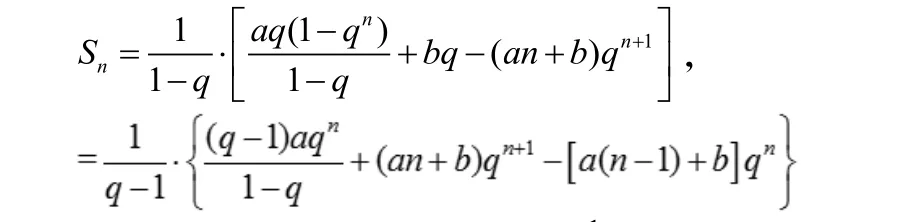
考虑到Sn中含有代数式参考引例，下用裂项法处理通项。

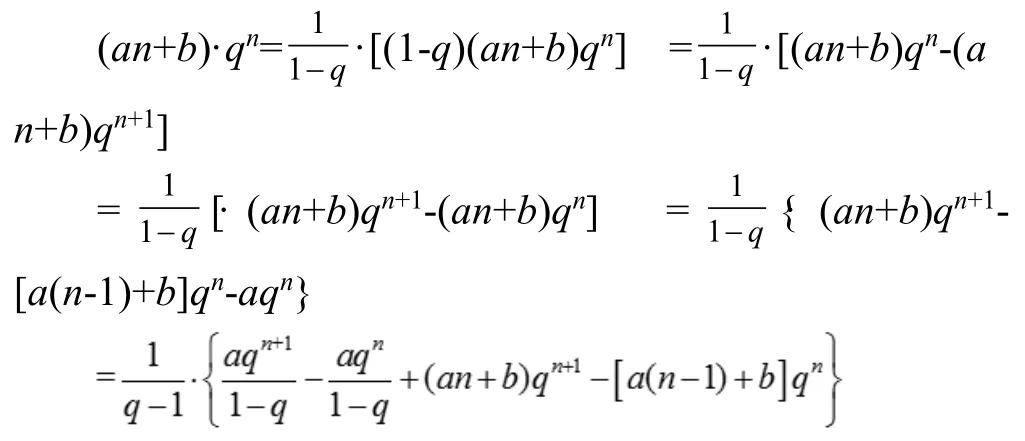
结论：“裂项法”对于一般数列｛（an+b）·qn｝其中a≠0,q≠0 且q≠1 的求和问题都适用。该方法更接近求和问题的本质，相比于以往常规的计算方法，运算过程学生更容易接受，解题思维也更加流畅自然。

（二）引申

对于一 般模型数列 ｛（an2+bn+c）·qn｝其 中a≠ 0,q≠ 0且q≠ 1的求和问题是否适用？

下面以一道具体事例进行探究：

例.求数列｛(n2+n)·2n｝的前n项的和Sn。

解法1：依然利用待定系数法，令

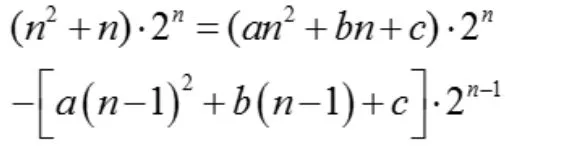
展开，对应系数相等，容易得到

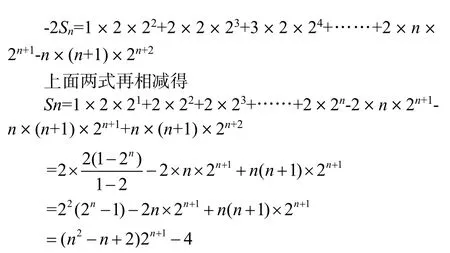
由此看来，“裂项法”也可以解决此类数列的求和问题，对于一般模型的验证过程，请有兴趣的读者可以试试。解法2 两次使用错位相减最终得到答案，进一步说明了“裂项法”与错位相减法的本质一致，方法同源，也进一步说明了这两种方法的普适应和统一性。

四、反思

（一）“裂项法”的一般性

从前面的典例研究过程中，不难发现，“裂项法”对于多项式数列*等比数列型的数列求和即an=(bm-1nm-1+bm-2nm-2+……+b1n+b0)qn型的数列求和问题都适用。下面以m次多项式*等比数列为例介绍一般操作方法：我们只研究q≠ 1的情形，设an=(λm-1nm-1+λm-2nm-2+……+λ1n+λ0)qn-(λm-1(n-1)m-1+λm-2(n-1)m-2+……+λ1(n-1)+λ0)qn-1将上式打开，按照降幂规则合并同类项，整理成如下形式：an=(μm-1nm-1+μm-2nm-2+……+μ1n+μ0)qn。其中μ0，μ1，……μm-1是用λ0，λ1，……λm-1，q来表示的一次式。利用对应系数相等得到一个m元一次方程组，用代入法可以解出λ0，λ1，……λm-1，接着用“裂项法”即可求出数列{an}的前n项和Sn=(λm-1nm-1+λm-2nm-2+……+λ1n+λ0)qnλ0不难看出，当多项式次数较高时，错位相减法就显得非常复杂了，“裂项法”的优越性就显而易见。

（二）裂项法使用的要点

裂项法在使用过程中需注意以下几点：

1.待定系数法确定裂项系数时，最好根据通项结构进行选择。如等。

2.选择不同的相邻项，对于下标n的取值有不同要求。如，引例法2 裂项求和中，最终n的取值需要从0开始，而变式1 中的n取值从1 开始。

3.无论哪一种方法，都要有首项验证的意识。

（三）从思想方法上看，数列求和的本质就是消项。

大家知道连续函数的定积分，根据牛顿—莱布尼茨公式，可以求出原函数后作差，而数列是离散型的函数，且“（xn）'=n·xn-1”因此形如｛（an+b）·qn｝类数列求和也可转化为“差”的形式。如：

(an+b)·q n=anq n+bq n=aq·(nqn-1)+bqn，这样问题转化为一个特殊数列｛n·qn-1｝和一个等比数列的求和问题，只要求出特殊数列｛n·qn-1｝的前n项的和，即可解决问题。在式子n·qn-1中，把q视作变量，联想到导数公式（xn）'=n·xn-1，故还可以用导数法来解决求和问题。

所以从数学本质上看，数列求和的根本方法是“裂项相消”（差分求和），故本文讨论的方法具有普适性。

通过以上讨论不难发现，在数列求和问题中，虽方法多样，但一定要看清本质，灵活选择。相比于传统方法，“裂项法”运用灵活广泛，思路简洁清晰，计算化繁为简，学生不容易出错，在掌握好错位相减法的基础上，再引导学生通过对数列通项的特征进行观察比较、挖掘通项本质内涵，更能进一步理解解题的思想和方法，增强解题能力和自信，从而有利于学生数学学科核心素养的培育。另外，新高考更注重对学生学科关键能力的考查，这就要求老师在课堂教学中，要有意识地引导学生多角度思考问题，经历多方法解决问题尤其是典型问题的探究过程不仅要实更要广，这不仅有助于加深老师对学科内容的理解也促使着学生在解题过程中形成有规律的程序化的解题思路，优化解法和快速准确解题，也提升了学生的数学逻辑思维能力和数学运算能力，还能让学生开拓了数学视野、坚定了学好数学的信心，更有利于学生的持续发展和多元发展。