罕遇地震下高层RC框架结构双地震动强度参数易损性分析

邓夕胜，赖馨粤，袁 凯，林嘉聪，朱一林

（1.西南石油大学土木工程与测绘学院，成都 610500；2.广元市城建投资集团有限公司，广元 628017）

引言

高层RC 框架结构在遭遇罕遇地震时，易发生较大的损伤甚至倒塌，研究高层RC 框架结构在遭遇罕遇地震时的易损性对结构在遭遇罕遇地震作用时可能发生的破坏做出估计，可以对评估地震灾害，加固改造既有建筑提供参考［1］。

高层结构的类型，地震动强度参数的选取对结构的易损性分析影响较大。周颖等［2］采用基于增量动力分析法（Incremental Dynamic Analysis，IDA）对某高层混合结构进行抗震性能分析，该方法可以用来评估复杂高层结构和高层混合结构；邓晖等［3］对超高层混合结构的地震动强度指标进行评估，发现采用考虑结构前a%振型质量参与系数的自振周期所对应谱加速度的几何平均值Sˉa%为地震动指标可以降低结果的离散性，更好地评估结构易损性；汪梦甫等［4］以同济大学模拟地震台试验的高层混合结构模型原型选用结构损伤指数DM（Damage Measure）和地震动强度参数IM（Intensity Measure）进行分析，得到IDA 曲线簇并直接用其绘制出地震易损性曲线，该分析结果与振动台试验结果吻合良好。

地震动强度参数的选取方面，KATSUICHIRO 等［5］基于copula 函数的双结构地震需求参数EDP（Earthquake Demand Parameter）建立维多利亚非延性钢筋混凝土框架双变量地震需求模型，根据预期地震损失和地震性能指标评估了双变量地震易损性及经济损失影响；ALICE 等［6］提出了考虑强度度量参数的异方差性并进行地震动参数的矢量组合绘制易损性曲面；高大峰等［7］考虑PGA和震级M，PGA和震中距R两组双参数对中国双层古建筑木结构的地震易损性影响，证明两个地震动参数可以提高木结构的易损性失效概率；陈立波等［8］基于双地震动强度指标，对典型桥墩易损性进行了研究，桥梁结构与双地震动强度指标比单一地震动强度指标更有效；李宁等［9］采用向量IM 指标对钢筋混凝土桥墩进行易损性分析，与标量IM 指标相比，考虑了两个地震动强度指标的相关性，形成的易损性曲面可以更好反映结构地震失效概率。

钱坤等［10］对高层建筑进行了罕遇地震下的静力弹塑性分析和动力时程分析，从各个方面评估该结构的整体可靠性，找到其薄弱部位并对提出了加固方法；黄彬辉等［11］对上海一个超限高层加固工程进行了罕遇地震下的弹塑性时程分析及抗震性能评价，验证了有限元软件建模的可靠性，结构能满足“大震不倒”的设计要求；潘玉华等［12］对某一超高层框架－核心筒结构进行罕遇地震下的弹塑性时程分析，寻找结构的薄弱部位，并对其进行加固后进行分析对比，结果表明加固后关键构件可以满足抗震性能限值。目前高层RC 框架结构在罕遇地震下易损性研究的相关报道较少，本文对高层RC 框架结构在罕遇地震下，考虑单一地震动强度参数及双地震动强度参数的地震易损性进行对比分析，研究高层RC 框架结构在罕遇地震下的抗震性能。

1 易损性理论

结构地震易损性表示在不同地震动强度的作用下结构达到特定损伤状态的概率［9］。易损性分析不仅是研究结构地震破坏程度的基础，还是结构地震破坏预测的组成部分，其在结构破坏和损失预测中都起着重要的作用。

1.1 单一地震动强度参数的易损性

由文献［13］结构损伤指数DM与地震动强度参数IM的关系如下：

式中：α和β为待拟合参数。

两端取对数得：

式中：a= lnα；b=β。a和b可由IDA分析后得到的数据进行回归分析拟合得到。

由文献［14－15］，结构的易损性曲线可由下式得到：

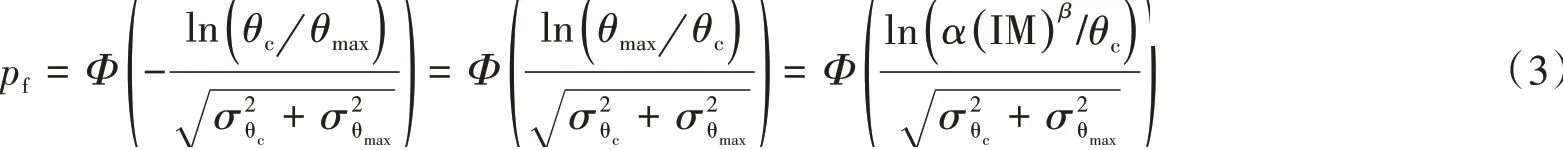
式中：pf为结构损伤超过某一性态点的概率；IM 代表PGA 及Sa（T1，5%）；不同破坏状态对应极限层间位移角θc可由IDA曲线读取分别为不同破坏状态对应极限层间位移角θc和最大层间位移角θmax的对数标准差，可由统计得到，或根据结构物易损性曲线参数高标准耐震设计规范FEMA（HAZUS-MH）［16］取值；Φ( )

x为正态分布函数，可以通过查标准正态分布表来确定。

1.2 双地震动强度参数的易损性

双地震动参数比单一地震动参数能反映更多的地震特性，可以对建筑物进行更全面地地震灾害评估［17］。当选取两个地震动参数时，由文献［17］可得：

式中：a、b和c为回归方程的回归系数；ϱe为相对于平面的残差平方和；n为样本数量；IM1和IM2分别为两个不同的地震动强度参数；σ^ 为离散性系数。

此时，地震易损性函数为：

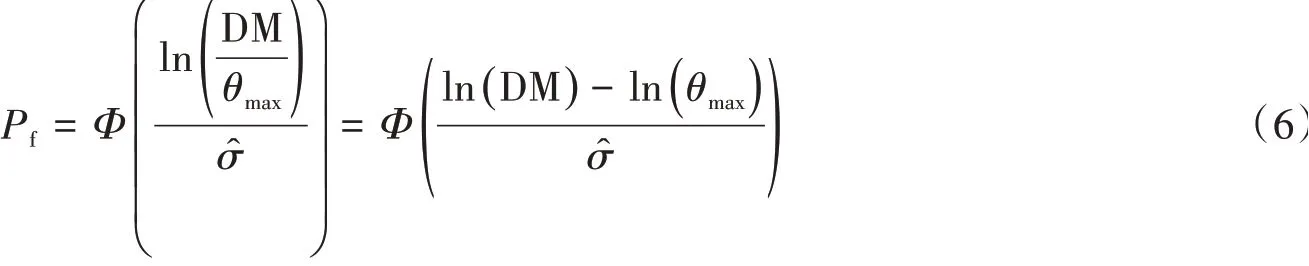
2 地震动强度参数和结构损伤指标的选取

IDA 分析受地震动强度指标选取的影响较大，地震动强度指标是衡量地面运动剧烈程度的重要参数。常用的地震动强度指标有地震动峰值地面加速度（PGA）、峰值速度（PGV）、峰值位移（PGD）和结构第一自振周期对应的谱加速度Sa（T1，5%）等。已有研究表明［18］对框架结构进行IDA 分析时，采用不同的地震动强度指标所得结果的离散程度有较大差异，其中：以PGA 和Sa（T1，5%）为地震动强度指标进行IDA 分析有效性较好，选取PGA和Sa（T1，5%）作为IM指标。

结构的损伤指标是评价结构性能状态的重要参数。常用的结构性能指标有最大层间位移角、顶点偏移率和节点转角等。最大层间位移角可以较为准确地反映出结构的损伤状态，由文献［19］，最大层间位移角与结构损伤程度、结构抗倒塌能力和节点转动情况等都有着直接的关系，能够较好地反映结构的抗震性能。选取最大层间位移角θmax作为结构的DM指标。

3 分析过程

3.1 模型建立

参考《混凝土设计规范》（GB 50010－2010）及《高层建筑混凝土结构技术规程》（JGJ 3－2010）等利用PKPM设计了一个11层RC框架结构，模型基本信息如下：

层高3.6 m，建筑总高度39.6 m，采用整体现浇楼盖，板厚为100 mm。建筑形状规则，每层梁柱的布置位置一致，选取1层结构平面图为例如图1所示。

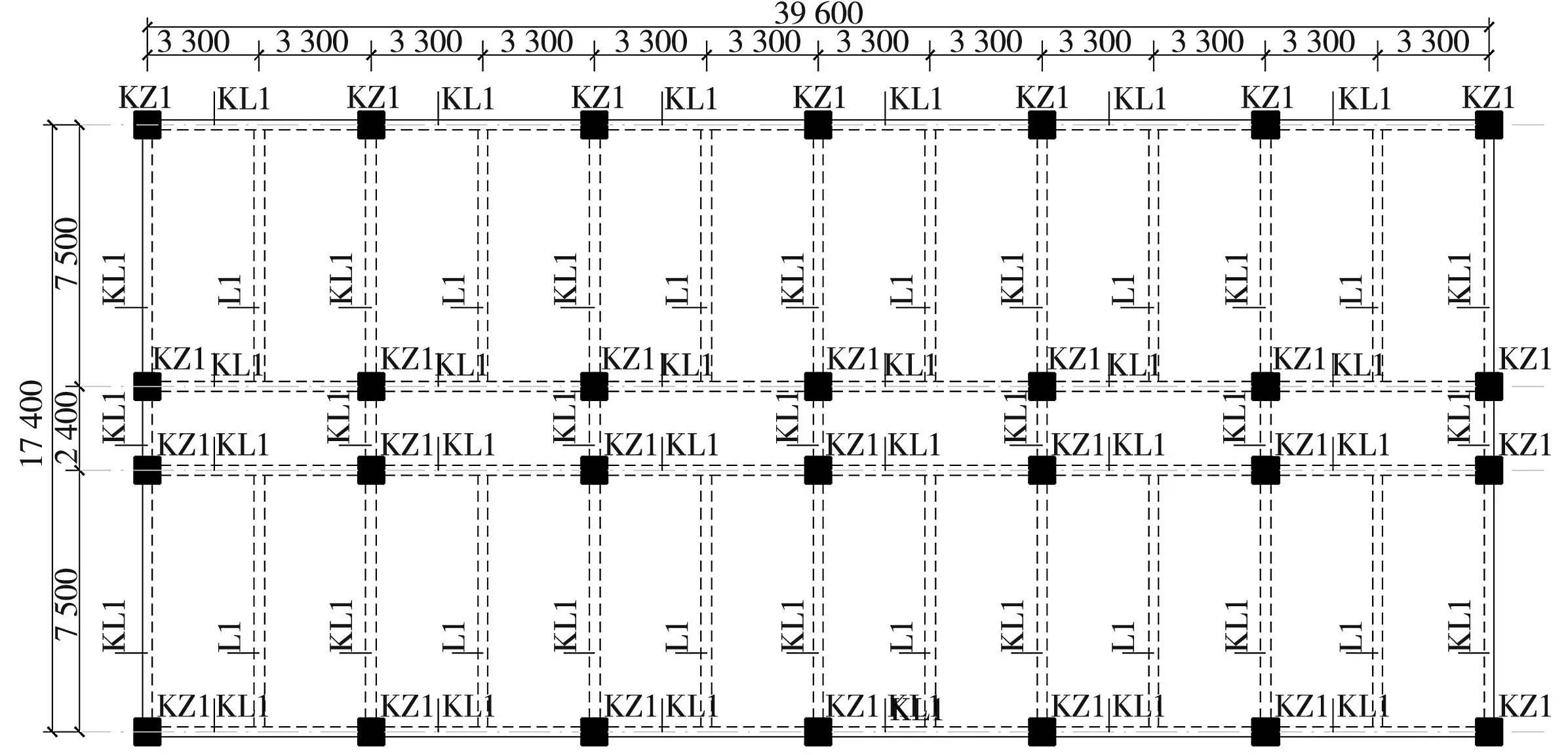
图1 层结构平面图Fig.1 Structural plan layout

设防地震分组为第三组，建筑场地类别为Ⅲ类，设防烈度区为7 度（0.1 g），结构阻尼比0.05。模型混凝土等级为C30，梁柱纵筋为HRB400，板纵筋为HRB400，箍筋为HPB300。荷载的施加：按《建筑结构荷载规范》（GB 50009－2012），楼面：4.6 kN/m2（恒），2.0 kN/m2（活）；屋面：5.0 kN/m2（恒），2.0 kN/m2（活）；填充内墙线荷载8.86 kN/m，填充外墙线荷载11.28 kN/m；屋顶女儿墙线荷载3.33 kN/m。

梁和柱截面尺寸见表1。

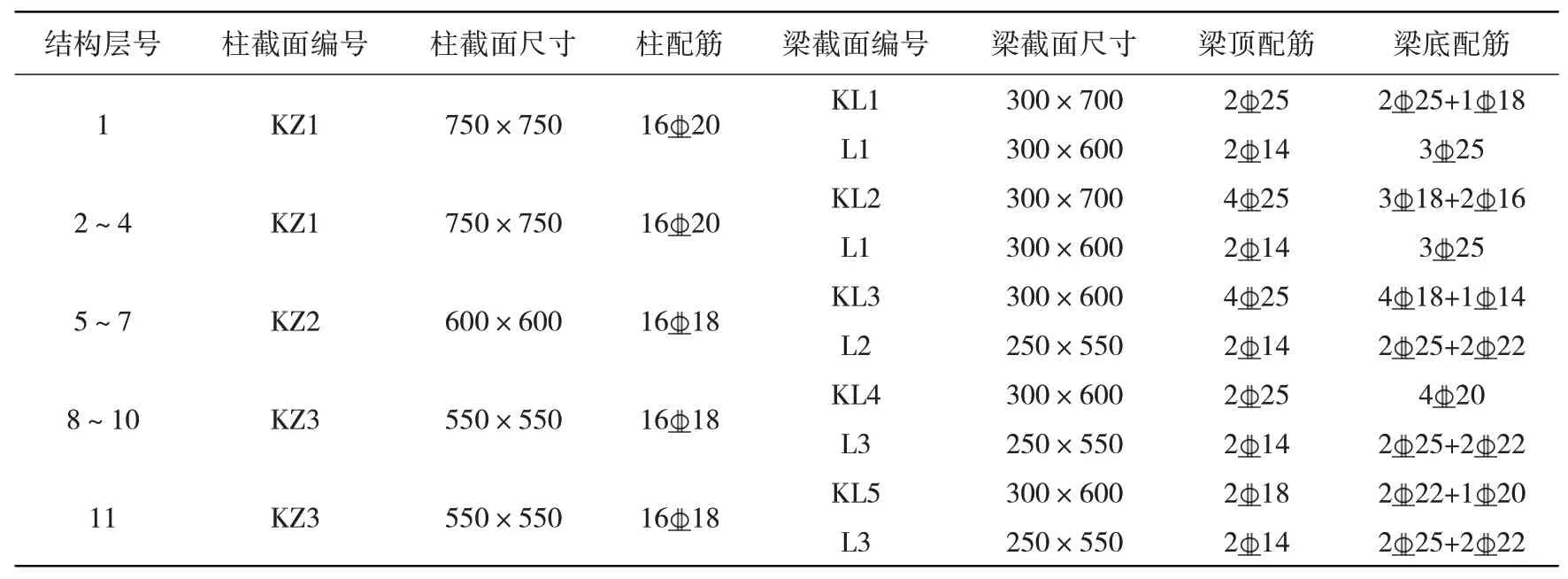
表1 结构基本信息Table 1 Basic information of structure

采用SAP2000 建立有限元模型，进行弹塑性时程分析，钢筋和混凝土本构关系参考《混凝土设计规范》（GB 50010－2010）附录C 中的钢筋及混凝土本构关系；梁柱节点采用选择SAP2000 中默认的铰属性，在梁上采用主方向的弯矩铰M3，在柱上采用P－M2－M3 铰，双向地震动输入，通过定义广义位移来获得结构损伤指标θmax，模型的配筋采用SATWE 计算满足相应规范要求后，再手动配筋建立的PKPM 模型如图2 所示。建立的有限元模型如图3所示。

图2 PKPM结构模型图Fig.2 Structure model layout of PKPM

图3 SAP2000有限元模型图Fig.3 Finite element model layout of SAP2000

3.2 模型验证

采用PKPM和SAP2000两种软件建立的模型前三阶自振周期对比见表2。

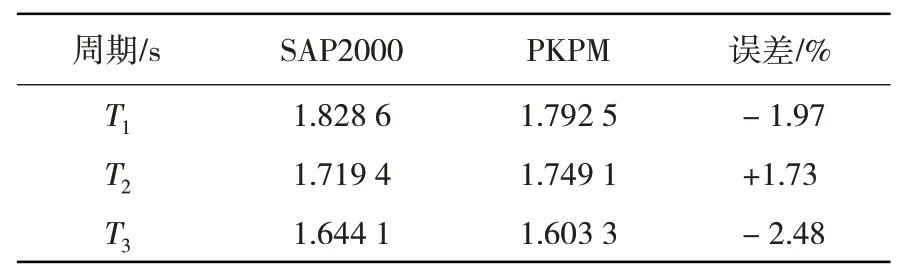
表2 模型前三阶周期对比Table 2 Comparison of the first three periods of the model

由表2 可知：前三阶周期比较接近，说明PKPM 模型和SAP2000 模型具有很好的相似性［3］。为验证SAP2000建模单元模拟的准确性，选用文献［20］的二维三层框架算例，SAP2000模态分析结果与试验对比见表3。

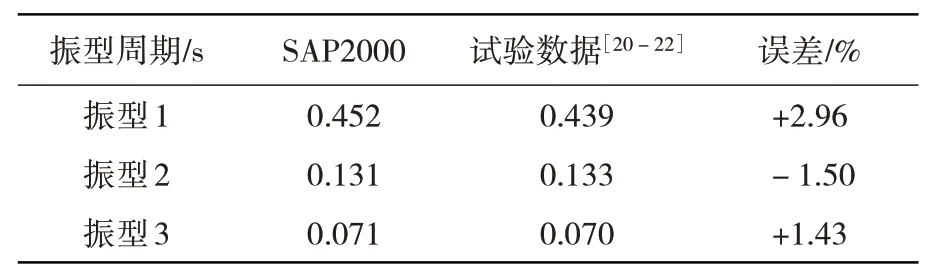
表3 模型周期计算对比Table 3 Comparison of model cycle calculation

由表3可知：采用本文的有限元建模分析与试验误差在允许范围内，表明利用SAP2000建立的有限元模型有工程参考价值。

3.3 地震动选取

由文献［20］，利用IDA方法评估一个中等高度的建筑结构，选用10～20条地震动，加上一个合适的地震动强度指标就可以得出相对准确的结论。

由美国（ATC－63）［23］报告的8 点地震动选取原则，从PEER 地震动数据库中，选取了符合Ⅲ类场地使用的21条地震动记录，以及3条人工地震动，地震动信息见表4。

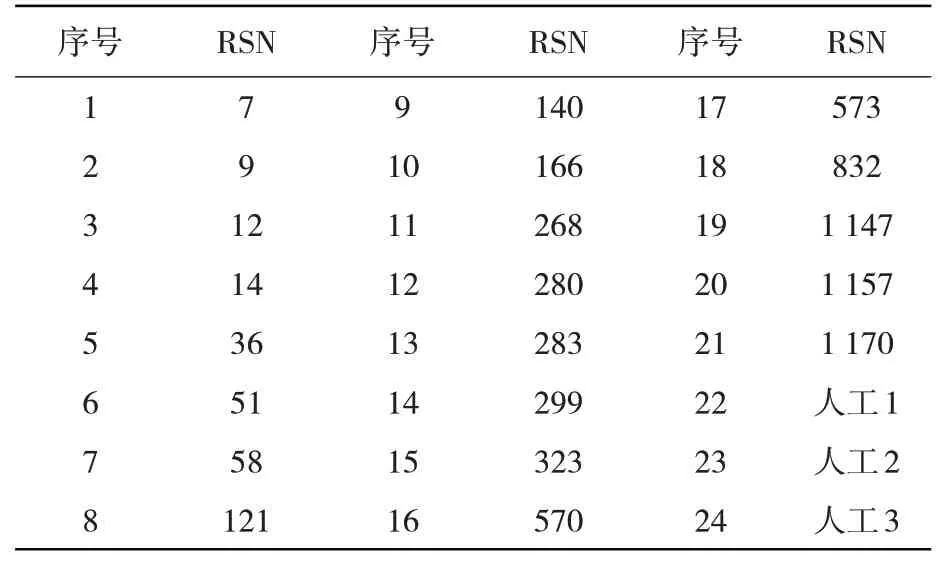
表4 地震动记录RSN信息Table 4 RSN information of ground motion records

3.4 非线性时程分析调幅方法及性能指标确定

地震动调幅方法分为三种［24］，等步长调幅计算量大，选用变步长调幅方法，根据收敛结果进行步长调整，提高计算效率。

以最大层间位移角为结构性能指标，FEMA（356）［25］规定，混凝土框架结构分为以下三种性能状态，不同性能状态对应的最大层间位移角限值参考见表5。

表5 不同性能状态下的最大层间位移角限值Table 5 Maximum interlayer displacement angle limits under different performance states

4 结果及分析

4.1 单一地震动强度参数IDA分析

4.1.1 基于PGA的IDA分析

以最大层间位移角θmax作为X 轴，峰值加速度作为Y 轴，用三次样条插值法将各点进行连接，结果如图4所示。选取16%、50%和84%的三个百分位曲线依据DM 准则统计图4 中的IDA 曲线，利用MATLAB 程序，将地震动强度PGA和最大层间位移角θmax的数据整理为绘制百分位曲线所需的数据，绘制百分位曲线，如图5所示。

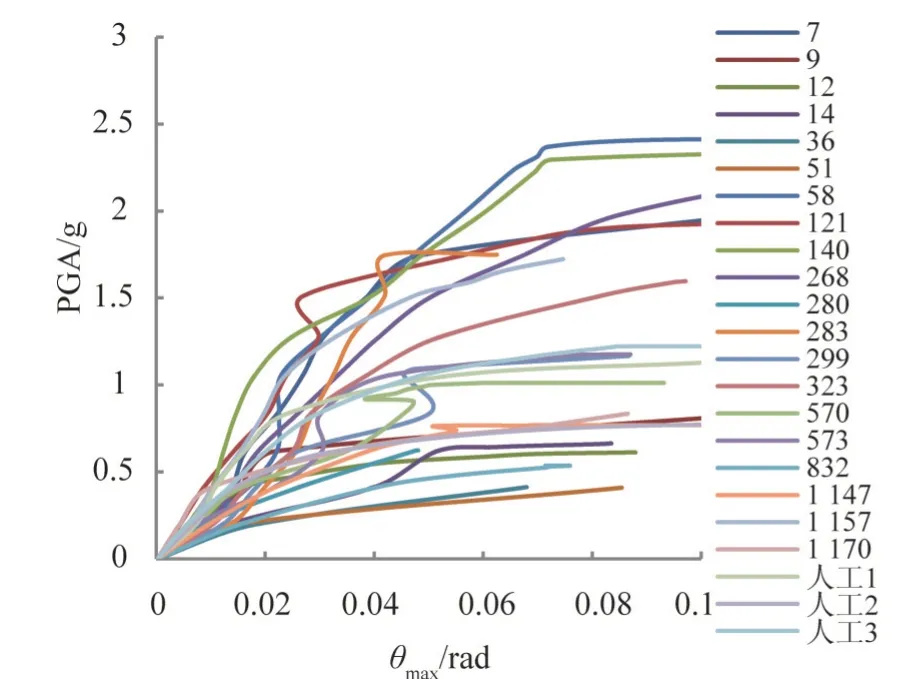
图4 基于PGA的IDA曲线Fig.4 IDA curve based on PGA

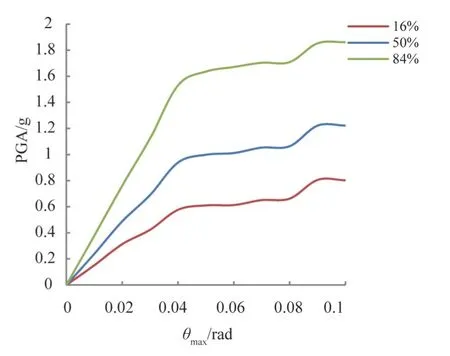
图5 基于PGA的百分位曲线Fig.5 Percentile curve based on PGA

由图5可得到不同性能状态的结构所对应的地震动强度指标PGA，见表4。

由表6 可知：24 条地震动中，当PGA=0.58 g，16%的地震动使结构倒塌；当PGA=0.94 g，50%的地震动使结构倒塌；当PGA=1.53 g，84%的地震动使结构倒塌。

表6 结构不同状态的地震动强度Table 6 Ground motion intensity of structures in different states

4.1.2 基于Sa（T1，5%）的IDA分析

以最大层间位移角θmax为X 轴，阻尼比5%时以结构基本周期对应的谱加速度值Sa（T1，5%）作为Y 轴，用三次样条插值法将各算得数据点进行连接，如图6 所示。选取16%、50%和84%的三个百分位曲线依据DM准则对图6中的IDA曲线进行统计，利用MATLAB程序，将地震动强度Sa（T1，5%）和最大层间位移角θmax的数据整理得到绘制百分位曲线所需数据，绘制百分位曲线，如图7所示。

图6 基于Sa的IDA曲线Fig.6 IDA curve based on Sa

图7 基于Sa的百分位曲线Fig.7 Percentile curve based on Sa

由图7可得到不同性能状态的结构所对应的地震动强度指标Sa（T1，5%），见表5。

由表7 可知：24 条地震动中，当Sa（T1，5%）=0.19 g，16%的地震动使结构倒塌；当Sa（T1，5%）=0.37 g，50%的地震动使结构倒塌；当Sa（T1，5%）=0.72 g，84%的地震动使结构倒塌。

表7 不同性态点对应的结构地震动强度Table 7 Seismic intensity of structures corresponding to different behavior points

4.2 单一地震动强度参数地震概率需求模型

对分析的数据进行汇总，对θmax和地震动强度参数（PGA，Sa（T1，5%））分别取对数，利用Origin2019 进行线性回归拟合分析，得到分别ln（PGA）和ln（Sa）为横坐标的地震概率需求模型，如图8－9所示。

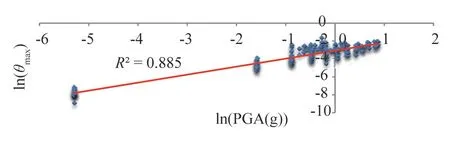
图8 基于PGA地震概率需求模型Fig.8 Earthquake probability demand model based on PGA

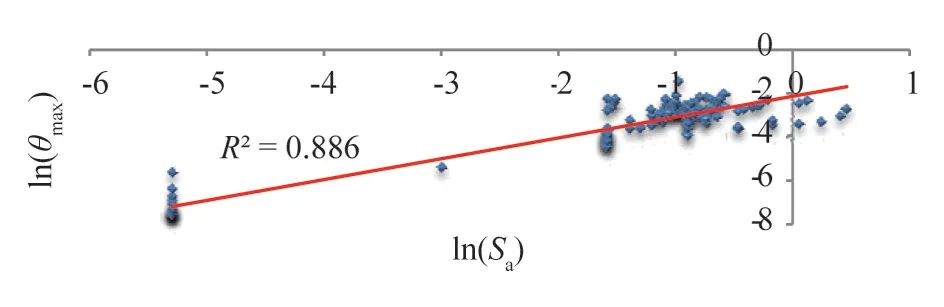
图9 基于Sa（T1，5%）地震概率需求模型Fig.9 Earthquake probability demand model based on Sa（T1，5%）

σ^2= 0.287 22，离散性参数σ^=0.535 93，由公式（2），拟合后的概率需求方程为：

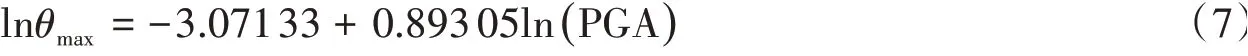
σ^2= 0.285 47，离散性参数σ^=0.534 29，由公式（2），拟合后的概率需求方程为：

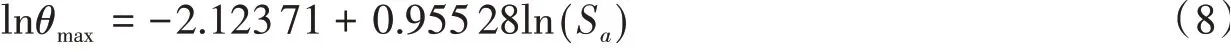
一般认为判定系数R2大于0.7可判定预测模型有效［26］，故线性拟合是有效的。

4.3 单一地震动强度参数地震易损性分析

由易损性理论可知：模型经线性回归得到的概率函数符合标准正态分布。

由公式（3）和公式（7），以PGA为地震动强度参数的失效概率公式为：

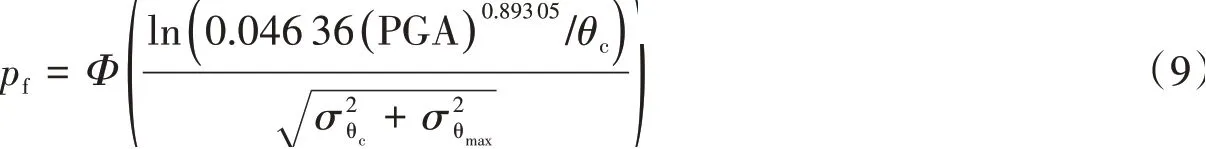
由公式（3）和公式（8），以Sa（T1，5%）为地震动强度参数的失效概率公式为：

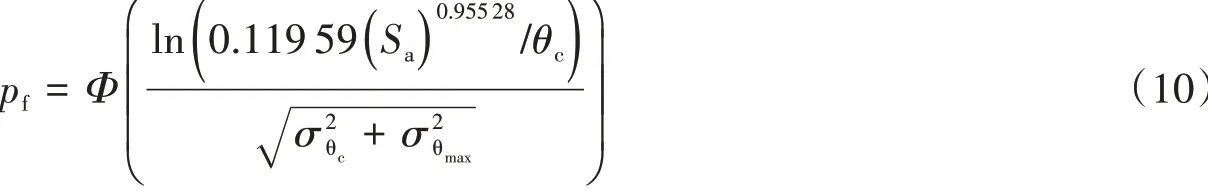
由文献［27］设防烈度为7 度，0.1 g 的地区，罕遇地震对应的，由图10 得

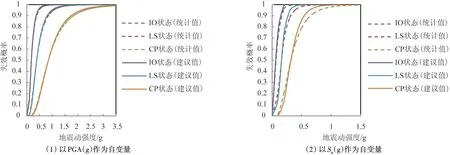
图10 二维易损性曲线Fig.10 Two dimensional vulnerability curves

到在罕遇地震下，采用统计值和采用建议值对应结构在不同性态点的失效概率，见表8。

表8 罕遇地震下失效概率对比Table 8 Comparison of failure possibilityunder rare earthquake

在美国（ATC－63）中建议：“在设防大震下倒塌概率小于10%即认为结构达到大震性能的要求”，以上结果表明，按照我国现行规范设计的高层框架结构能达到大震不倒的性能要求。考虑统计值和建议值的差异性，由表6可知：在罕遇地震下，按统计值得出的结构的IO 状态失效概率比按建议值得出的结构失效概率偏低，但LS和CP状态的结构失效概率偏高，但均能满足大震不倒的性能要求。

4.4 双地震动强度参数地震概率需求模型

以ln( PGA )，ln(Sa(T1,5% ))为自变量，以ln(θmax)为因变量，用Origin2019进行线性回归分析，回归曲面如图11所示。

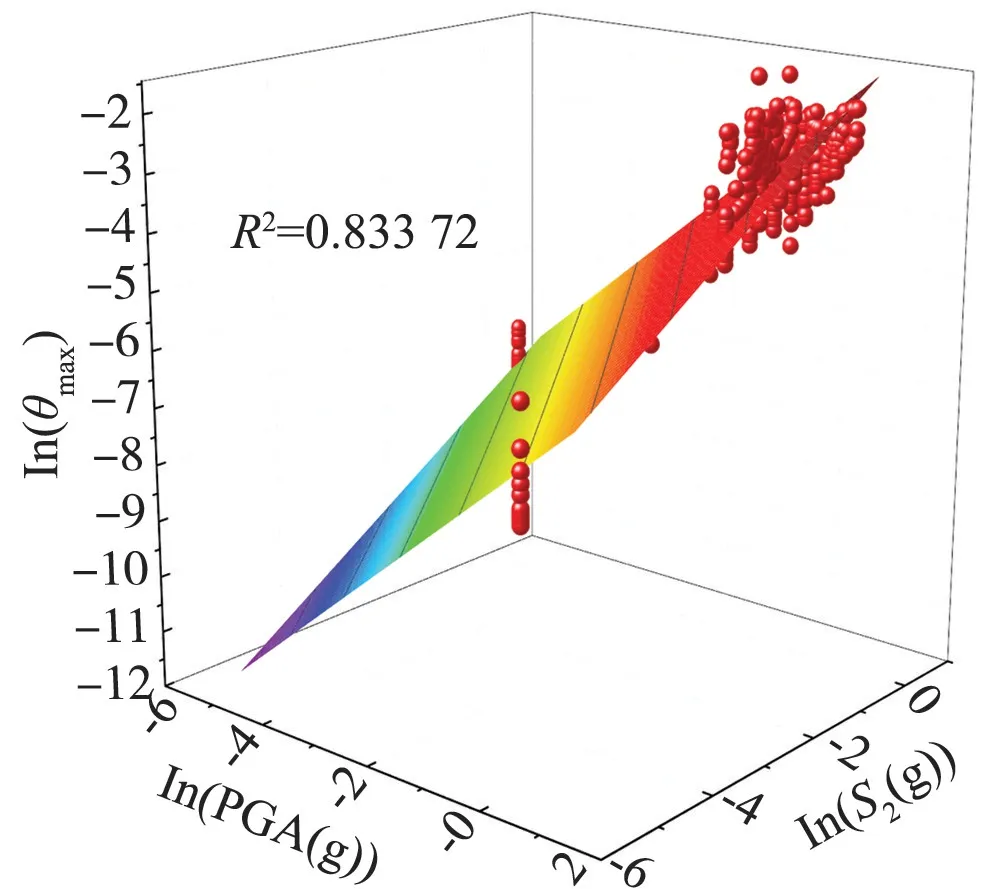
图11 拟合曲面图Fig.11 Fitting surface diagram

R2=0.833 72，表明PGA和Sa（T1，5%）对θmax有良好的预测效果。

由公式（4），拟合后的概率需求方程为：

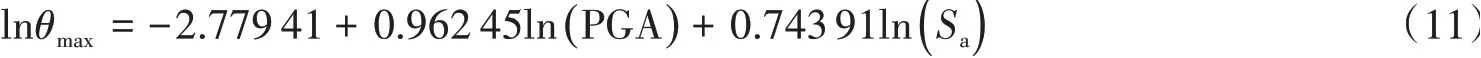
三种情况的离散参数对比见表9。

表9 三种情况的离散性参数Table 9 Discreteness parameters in three cases

由表9 可知，基于PGA 和Sa（T1，5%）的需求拟合离散性系数最大，基于PGA 的需求方程拟合次之，基于Sa（T1，5%）的需求方程拟合离散性最小。

4.5 双地震动强度参数地震易损性分析

选择两个地震动强度参数PGA，Sa（T1，5%），对其分别取对数，以最大层间位移角为损伤指标，也对其取对数，绘制易损性曲面，由公式（6）和公式（8）得失效概率公式为：

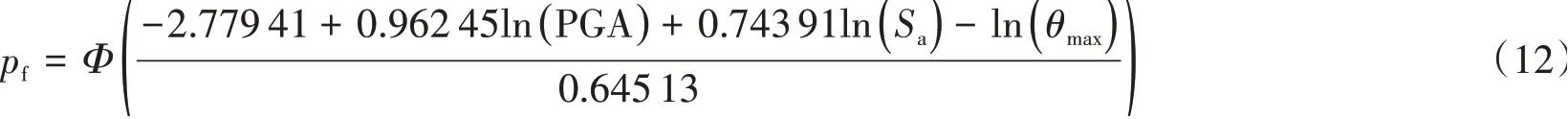
根据不同性能状态绘制易损性曲面如下：

由图12 可知：7 度区，0.1 g 抗震设防状态下，罕遇地震下，即根据文献［27］，PGA=0.22 g 时，结构失效概率随S（aT1，5%）的增大而增大；Sa(T1,5%)大震=0.14 g时，结构失效概率随PGA 的增大而增大；在三种状态曲面两侧缓陡情况基本相近，表明S（aT1，5%），PGA 对结构失效概率的影响相当；如图13 所示，罕遇地震下，采用易损性曲面得到的结构失效概率远小于采用单一地震动强度参数得到的失效概率。

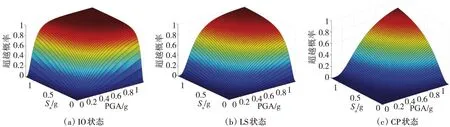
图12 PGA和Sa（T1，5%）组成的易损性曲面Fig.12 Vulnerability surfaces diagram composed of PGA and Sa（T1，5%）

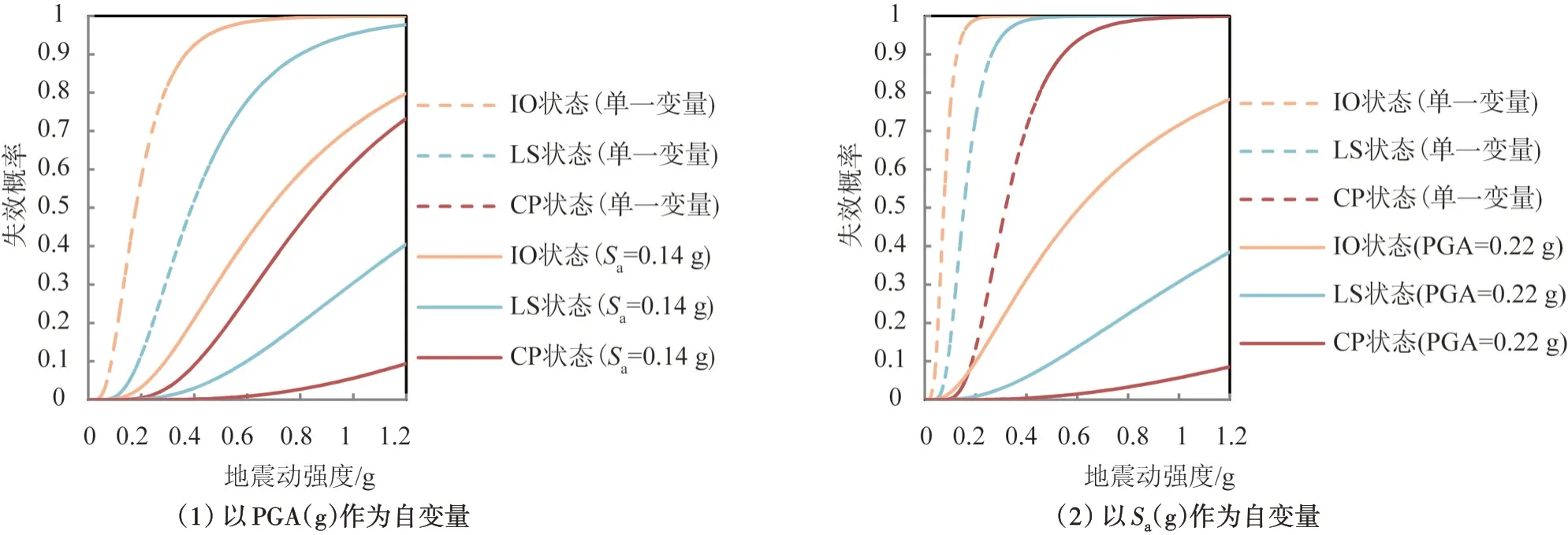
图13 罕遇地震失效概率对比Fig.13 Comparison of failure possibility under rare earthquake

4.6 结构易损性分析对比

为更好地研究基于PGA 和Sa（T1，5%）的易损性曲面模型，对易损性曲面模型和单一地震动强度参数的易损性曲线模型进行对比分析，单一地震动强度参数PGA，Sa（T1，5%）下结构的失效概率基本相当，即对结构损伤的影响基本相当，故只考虑固定PGA，Sa（T1，5%）由小到大变化结果如图14所示。

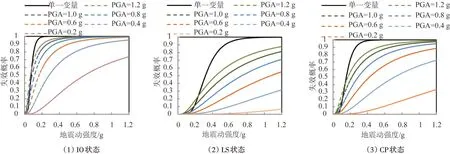
图14 结构易损性模型对比Fig.14 Comparison of structural vulnerability models

见表10，结构在IO 状态、LS 状态和CP 状态下易损性曲面失效概率小于单一地震动强度参数的失效概率，且随着PGA的增大，失效概率接近且逐渐超过第一地震动强度的失效概率，表明采用易损性曲面更能反应结构的损伤程度。美国（ATC－63）中建议：“在设防大震下倒塌概率小于10%即认为结构达到大震性能的要求”，即基于两种不同的地震动参数来看：本文按照我国现行规范设计的高层框架结构均能达到大震不倒的要求，但在基于易损性曲面的失效概率来看：在大震作用下，随着PGA的增加，结构可能会发生倒塌。

表10 不同状态失效概率对比Table 10 Comparison of failure probability in different states %

5 结论

采用单一地震动强度参数（PGA，Sa（T1，5%））和双地震动强度参数（PGA和Sa（T1，5%））对高层RC框架结构进行罕遇地震下的易损性分析，得到的结论如下：

（1）罕遇地震下，采用双地震动强度参数结构失效概率明显低于采用单一地震动强度参数结构失效概率。

（2）高层RC 框架结构，采用单一地震动强度参数PGA 比Sa（T1，5%）离散性高了0.001 64；双地震动强度参数离散性比Sa（T1，5%）增大了0.110 84，比PGA 增大了0.109 2；三种类型离散性相差较小，采用双地震动强度参数进行易损性分析反映的地震动信息更全面。

（3）采用HAZUS99建议值得到的单一地震动强度参数结构失效概率公式对结构易损性评估得出的结论偏于保守；在CP状态下，基于PGA的结构失效概率按统计值计算比按建议值增大了0.4%，基于Sa（T1，5%）的结构失效概率按统计值计算比按建议值增大了4.6%，Sa（T1，5%）受结构影响较大。采用双地震动强度参数得到的结构失效概率公式更能真实量化不同强度地震作用下结构的失效概率。