碟形弹簧自复位梁柱钢节点受力性能分析

朱丽华，韩 伟，宁秋君，刘海林

（1.西安建筑科技大学省部共建西部绿色建筑国家重点实验室，陕西西安 710055；2.西安建筑科技大学土木工程学院，陕西西安 710055）

引言

自复位结构体系由复位元件和耗能元件组成，地震作用时由耗能元件耗散地震能量，地震之后通过复位元件实现结构的复位性能［1］。自复位结构具有残余变形小，震后能快速恢复等优势，因此受到国内外研究者的广泛关注。1991 年，美国PRESS 计划首次提出关于自复位结构的概念［2］。2001 年，RICLES 等［3］提出了由预应力钢绞线复位的自复位钢框架节点；2002 年，RICLES 等［4］对9 个大比例的后张拉自复位钢框架节点进行了试验研究；2008 年，GARLOCK 等［5］研究了不同设计参数对后张拉自复位钢框架体系抗震性能的影响。ROJAS 等［6］和WOLSKI等［7］提出了由预应力钢绞线复位的自复位钢框架梁柱节点，并进行了试验研究；2011 年，潘振华等［8］提出了由钢绞线提供弹性恢复力的自复位钢框架节点，并通过参数分析研究了该节点的抗震性能；2020 年，QIN 等［9］提出了由后张拉预应力钢绞线提供弹性恢复力的自复位钢框架节点，研究了钢绞线预应力对该节点抗震性能的影响；HUANG 等［10－11］通过对后张拉自复位钢框架节点进行低周往复加载试验和有限元分析，研究了该节点的初始刚度，并提出了后张拉自复位钢框架的设计方法；2021 年，HUANG 等［12］通过有限元分析研究了后张拉自复位钢框架体系在不同地震作用下的抗震性能；FANG 等［13］、XU 等［14］和WANG 等［15］提出了碟形弹簧自复位阻尼器，并通过拟静力试验研究了碟形弹簧自复位阻尼器的抗震性能。

目前，自复位结构主要由预应力钢绞线或预应力筋提供弹性恢复力，但预应力钢绞线自复位节点的安装方式相对困难；在荷载的长期作用下，会出现钢绞线松弛和预应力下降等问题，进而影响结构复位能力。针对上述问题，本文提出了一种碟形弹簧自复位梁柱钢节点，该节点的复位和耗能原理与普通钢绞线自复位节点基本相同，其安装方式比普通钢绞线自复位节点简单；此外，通过对碟形弹簧的合理设计能有效控制预应力下降的问题。

1 碟形弹簧自复位节点构造与受力分析

1.1 自复位节点构造

碟形弹簧自复位节点的基本构造如图1（a）所示，该节点由碟簧装置提供弹性恢复力，由腹板摩擦耗散地震能量。碟簧装置由单耳板、外管、碟簧、拉杆和垫块组成，碟簧参数包括外径D、内径d、自由高度H0、碟簧厚度t、压平时变形量h0以及圆锥角θ，如图1（b）所示。碟簧装置具体构造如图1（c）所示，单耳板与外管通过螺纹连接，碟簧两端设置有垫块，并以拉杆作为内导杆，以外管作为外导管，由碟簧提供弹性恢复力，其受力主要由拉杆传递。拉杆受拉时碟簧产生径向变形，为保证碟簧变形不受阻，碟簧与外管和拉杆之间均设置有一定间隙。安装自复位节点时，应先将摩擦板和双耳板焊接在钢柱加强板上，再将钢梁和摩擦片安装在摩擦板之间，并通过高强螺栓固定，最后安装碟簧装置；该节点主要以螺栓连接为主，具有较好的可安装性。

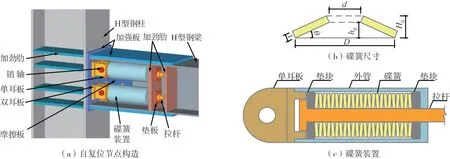
图1 碟形弹簧自复位节点Fig.1 Configuration of self-centering connection with disc springs

1.2 自复位节点受力分析［16－18］

自复位节点的受力分析如图2所示，开口之前，梁柱节点不发生相对转动，此时，自复位节点可等效为传统的刚性节点，其初始刚度k0可根据结构力学力法计算。

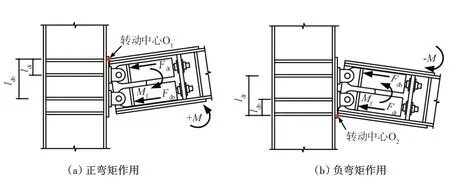
图2 自复位节点受力分析Fig.2 Force decomposition of self-centering connection

自复位节点的开口弯矩主要由弹簧预压力和腹板摩擦力提供，因此节点的开口弯矩为：

式中：F0为弹簧预压力；ldt和ldb分别为上部碟簧装置和下部碟簧装置至转动中心的距离；Mf为腹板摩擦力矩，可采用微元法计算，如图3所示，其计算公式为：

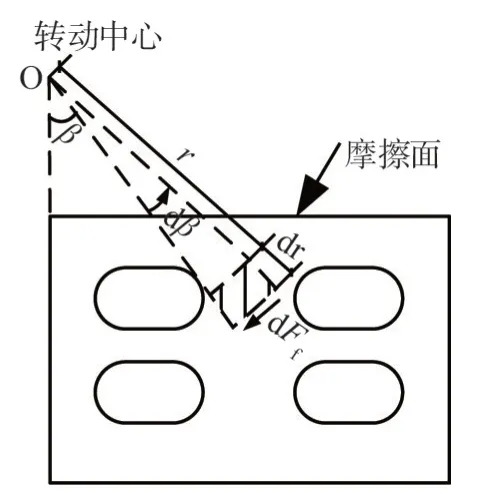
图3 摩擦力矩计算简图Fig.3 Calculation diagram of friction moment

式中：μ为摩擦耗能装置的摩擦系数；P为摩擦面单位面积压力；Nb为单个高强螺栓预紧力；nb为高强螺栓个数；S为有效摩擦面面积。

自复位节点开口之后的刚度主要由碟簧装置决定，因此节点开口之后的转动刚度为：

式中：kd为碟簧装置的刚度；n为碟簧叠合片数；fM为碟簧锥面间摩擦系数；α为碟簧压板处的摩擦面数；fR为碟簧承载力边缘处的摩擦系数；ks为复合碟簧的组合刚度。

自复位节点开口之后，摩擦力矩不再增加，节点的弯矩增量主要来自于碟簧装置，因此节点的抗弯承载力为：

式中：θ为梁柱节点的相对转角。

碟形弹簧自复位梁柱钢节点的耗能性能是重要的性能指标之一，通常以等效阻尼比ξeq作为衡量指标，可根据式（7）计算：

式中，ED为自复位节点单周滞回耗能；ES为同等线弹性体系达到相同位移时所储存的应变能。

2 有限元建模及分析

2.1 碟形弹簧建模及验证

碟形弹簧是该自复位节点的关键部件，其力学性能对节点的受力性能影响很大，本文以文献［17］中单片碟簧的试验结果为依据，对碟簧的有限元模拟方法进行验证，其中碟簧外径为200 mm，内径为102 mm，厚度为8 mm，自由高度为15 mm。采用ABAQUS 建立单片碟形弹簧有限元模型，并将有限元模拟结果与文献［17］的试验结果进行对比，如图4 所示。由图可知：数值计算结果与理论计算结果较为接近，与试验结果有微小差异，整体而言，三种结果基本一致。由此可见：碟形弹簧有限元模拟的方法是可行的。

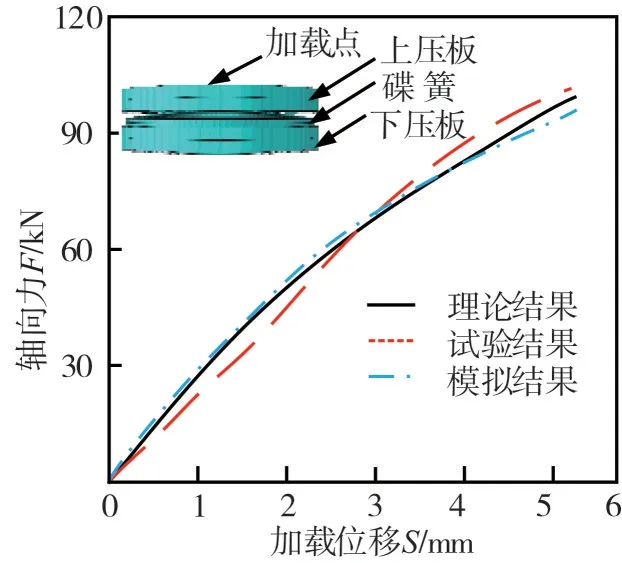
图4 单片碟簧有限元模型及结果对比Fig.4 Finite element model ofsingle discspring and results comparison

2.2 碟形弹簧自复位节点建模

碟形弹簧自复位梁柱钢节点的尺寸如图5所示，钢柱和钢梁均设置有厚度为20 mm 的加劲肋和加强板。碟簧外径为120 mm，内径为37.2 mm，碟簧厚度为9 mm，碟簧减薄厚度为8.5 mm，自由高度为11.7 mm。碟簧装置由24 片碟簧串联而成，其刚度为5.67 kN/mm，除单耳板与外管之间建立绑定约束外，其余部件之间均建立摩擦接触。钢梁与碟簧装置通过 36的10.9级高强螺栓连接，在钢柱的翼缘上焊有厚度为14 mm 的摩擦板，在摩擦板与钢梁腹板之间设置有2 mm 厚的黄铜摩擦片，摩擦片和钢梁腹板均设置有长圆孔，其中摩擦板和摩擦片均设置在钢梁腹板的两侧，并通过 22 的10.9 级高强螺栓与钢梁固定。碟形弹簧采用屈服应力为1 400 MPa 的60Si2MnA 合金钢，耳板和销轴均采用屈服应力为980 MPa 的35 CrMo 合金钢，其余构件均为Q345B。钢材的弹性模量均为2.06×105MPa，泊松比均为0.3，其本构模型均采用双线性随动强化模型，其中强化模量为0.01E。

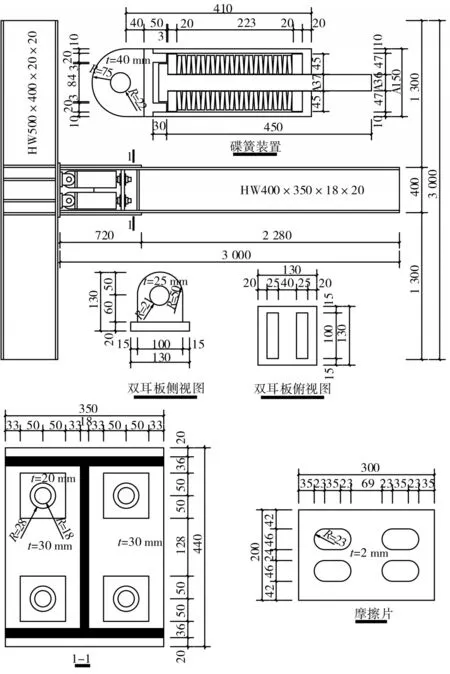
图5 自复位节点构造及尺寸Fig.5 Dimension and detail of self-centering connection

柱顶和柱底均设置铰约束，并在梁端分级施加低周往复荷载，第一级的位移值为5 mm；第二级的位移值为10 mm，以后各级的位移值按14 mm 增大，位移最大值为150 mm，对应的层间位移角为5%，每一级位移加载1 次，共计12 次。碟簧预压力和螺栓预紧力分别为80 kN 和30 kN，二者均通过Bolt Load 施加。构件之间的相互作用根据工程实际建立，其中钢构件之间的摩擦系数为0.2，碟簧锥面间的摩擦系数为0.03，碟簧承载力边缘处的摩擦系数为0.03，黄铜摩擦片与钢梁腹板之间建立绑定约束，摩擦片和摩擦板之间的摩擦系数为0.35。碟形弹簧自复位梁柱钢节点有限元模型如图6所示。

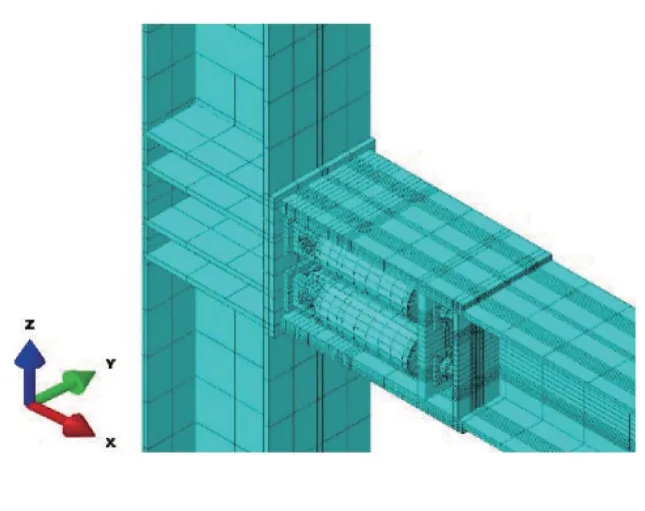
图6 自复位节点有限元模型Fig.6 Finite element model of self-centering connection

2.3 分析结果

理论计算结果和有限元计算结果见表1，表中：θmax为最大层间位移角；Mmax为最大层间位移角所对应的弯矩。由表1 可知：有限元计算结果与理论计算结果的误差较小，其中最大误差仅为7.13%。由此可见：碟形弹簧自复位梁柱钢节点的有限元建模方法准确可行。

表1 计算结果对比Table1 Calculation results comparison

碟形弹簧自复位节点的有限元计算结果如图7所示，由图可知：钢梁的最大应力为334.5 MPa，碟簧的最大应力为1 113 MPa，自复位节点基本处在弹性阶段；自复位节点的滞回曲线如图8所示，该节点的弯矩－转角曲线关于原点对称，为典型的“双旗帜形”。节点的开口弯矩为95.05 kN·m，当层间位移角为5%时，节点的抗弯承载力为149.74 kN·m。在开口之前，自复位节点几乎不发生相对转动，弯矩－转角曲线基本保持线性，节点的初始刚度为9.79 kN/mm，具有较好的初始刚度；开口之后，自复位节点的刚度明显下降，节点的弯矩－转角曲线也基本保持线性；自复位节点卸载时的刚度与加载时的刚度基本一致，荷载卸载到零时，节点的相对转角也接近于零。当层间位移角为2%时，节点的残余变形低于0.2%，符合震后可修复的性能要求［19］。由此可见：碟形弹簧自复位节点具有较好的自复位能力。

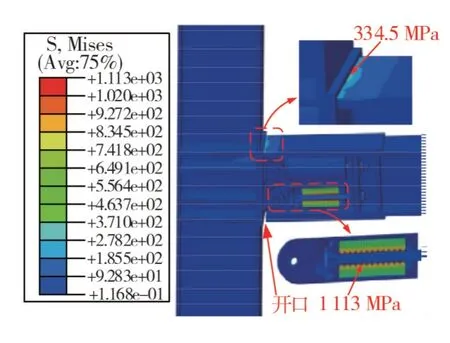
图7 自复位节点有限元计算结果Fig.7 Finite element analysis results of self-centering connection

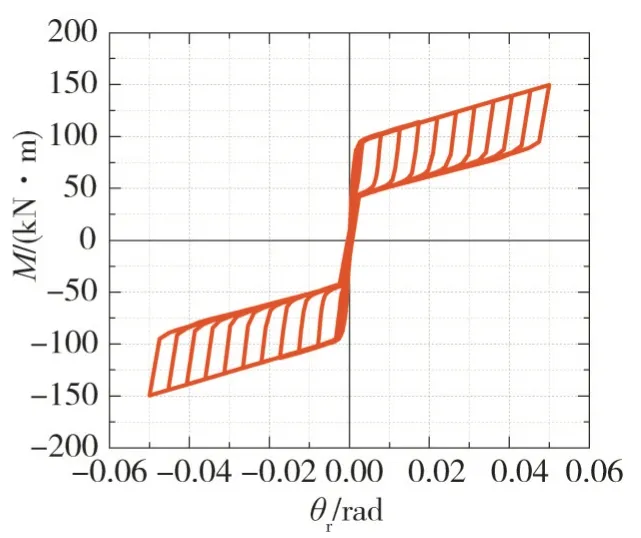
图8 自复位节点滞回曲线Fig.8 Hysteric response of self-centering connection

3 参数分析

3.1 计算结果

碟形弹簧自复位梁柱钢节点有限元分析结果见表2，表中：FB为腹板摩擦耗能装置的螺栓预紧力；FS为碟簧装置的弹簧预压力；θres为自复位节点的残余变形。

3.2 腹板摩擦耗能装置的螺栓预紧力

为考察腹板摩擦耗能装置的螺栓预紧力对自复位节点受力性能的影响，分析了螺栓预紧力分别为30 kN、45 kN和60 kN，其他参数不变的情况下自复位节点的受力性能。

由表2和图9（a）可知：螺栓预紧力对自复位节点开口弯矩和抗弯承载力的影响较大，但对节点初始刚度和开口后刚度的影响较小。螺栓预紧力增大时，滞回曲线变得更饱满，摩擦力矩也会随之增大，从而增大节点的开口弯矩和抗弯承载力。

由表2 可知：螺栓预紧力从30 kN 增加到45 kN 时，等效阻尼比增加了33.3%，残余变形增加了133%；螺栓预紧力从45 kN 增加到60 kN 时，等效阻尼比增加了18.9%，残余变形增加了23.3%。由图9（b）和图9（c）可知：随着螺栓预紧力的增大，自复位节点的耗能能力也会随之增大，但自复位节点的复位能力却随之下降。虽然增大螺栓预紧力会使自复位节点的复位能力下降，但节点的残余变形仍然较小，当螺栓预紧力为60 kN 时，节点的残余变形仅为0.164%，自复位节点仍然具有较好的复位能力，因此增大螺栓预紧力能有效提高自复位节点的耗能能力。

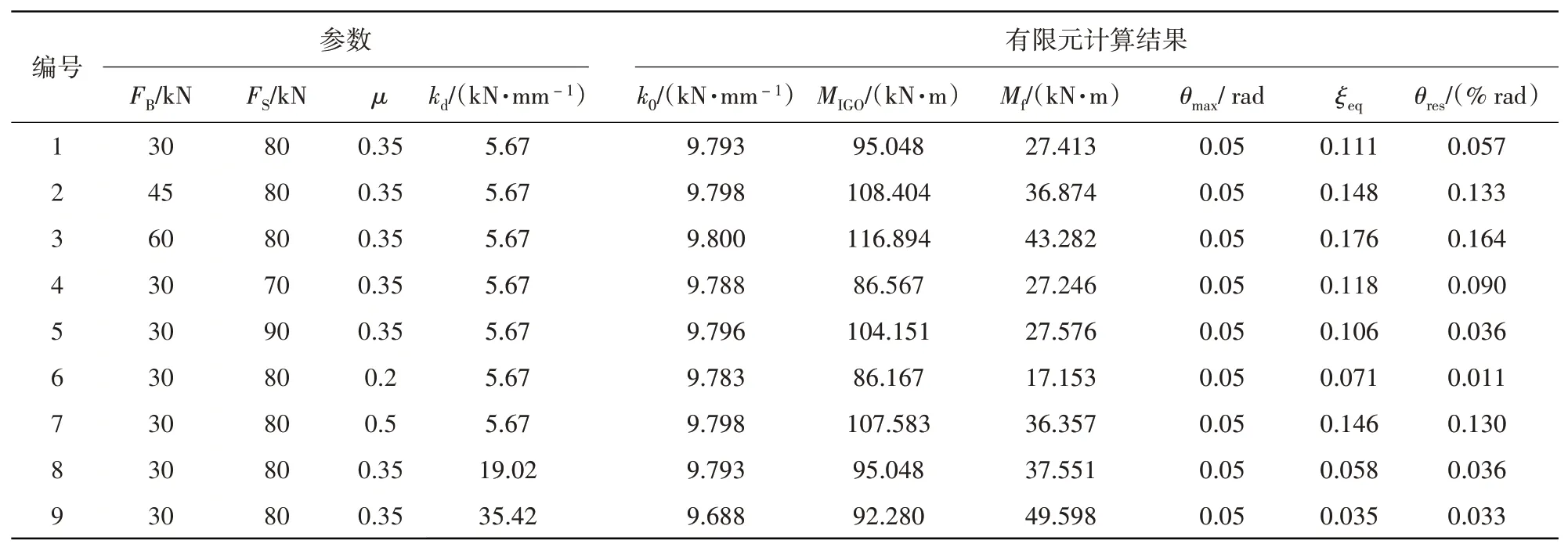
表2 有限元计算结果Table 2 Finite element method calculation results

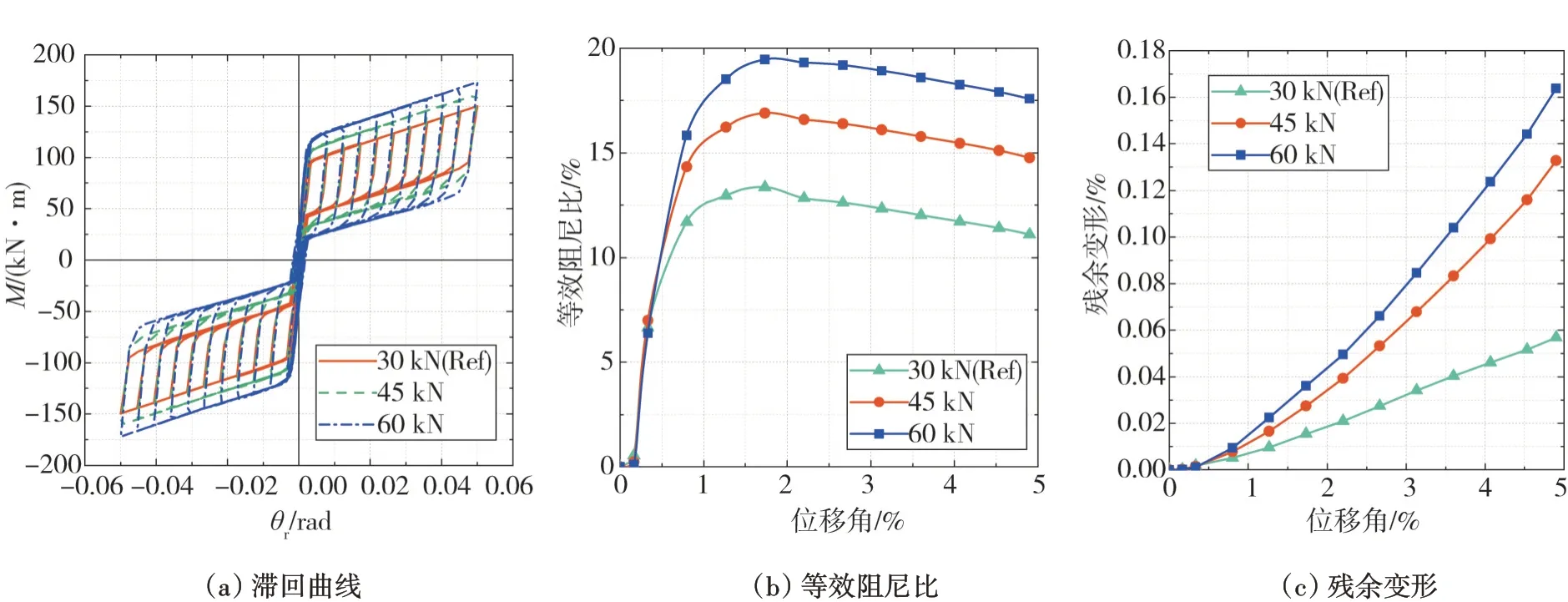
图9 螺栓预紧力对自复位节点力学性能的影响Fig.9 Effects of the bolt preload on mechanical properties of self-centering connection

3.3 弹簧预压力

考察了弹簧预压力分别为70 kN、80 kN和90 kN，其他参数不变的情况下自复位节点的受力性能。由表2 和图10（a）可知：弹簧预压力对自复位节点开口弯矩和抗弯承载力的影响较大，但对节点初始刚度和开口后刚度的影响较小。弹簧预压力增大时，弹簧力矩也会随之增大，从而增大自复位节点的开口弯矩。自复位节点的初始刚度与刚性节点的刚度近似相等，自复位节点开口之后的刚度由碟簧装置决定，因此弹簧预压力对自复位节点初始刚度和开口后刚度的影响较小。

由表2 可知：弹簧预压力为70 kN、80 kN 和90 kN 时，自复位节点的等效阻尼比分别为0.118、0.111 和0.106。弹簧预压力从70 kN 增加到80 kN 时，自复位节点的残余变形下降了36.7%；弹簧预压力从80 kN 增加到90 kN 时，自复位节点的残余变形下降了36.8%。由图10（b）和图10（c）可知：弹簧预压力对自复位节点耗能能力的影响较小，但对节点复位能力的影响较大，并且随着弹簧预压力的增加，节点的复位能力也会随之增大，因此增加弹簧预压力能有效提高自复位节点的复位能力。

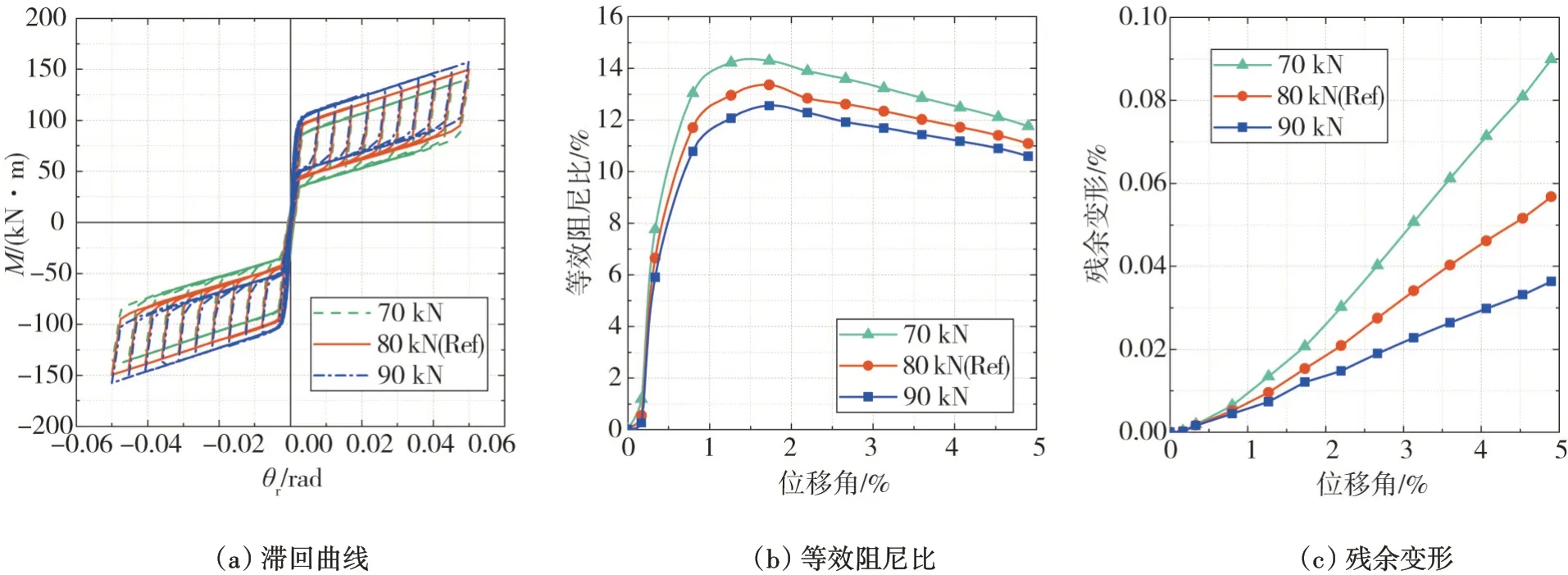
图10 弹簧预压力对自复位节点力学性能的影响Fig.10 Effect of spring preloads on mechanical properties of self-centering connection

3.4 摩擦系数

摩擦系数是影响自复位节点腹板摩擦耗能装置的重要参数，为研究摩擦系数对自复位节点受力性能的影响，分别研究了摩擦系数为0.2、0.35和0.5，其他参数不变的情况下自复位节点的受力性能。

由表2 和图11（a）可知：摩擦系数对自复位节点开口弯矩和抗弯承载力的影响较大，但对节点初始刚度和开口后刚度的影响较小。摩擦系数增大时，自复位节点的摩擦力矩也会随之增大，从而增大节点的开口弯矩和抗弯承载力。

综上所述，经产前彩超检查能够发现胎儿的肺内异常病灶，有利于对其病理性质和变化进行监测，因此常规的产前超声检查对于胎儿肺内病灶的发现以及评估和预后均有十分重要的价值。

由表2 可知：摩擦系数从0.2 增加到0.35 时，自复位节点的等效阻尼比增加了56.3%，残余变形增加了418%；摩擦系数从0.35增加到0.5时，自复位节点的等效阻尼比增加了31.5%，残余变形增加了128%。由图11（b）和图11（c）可知：增大摩擦系数能有效提高自复位节点的耗能能力，但节点的残余变形也会随之增大。虽然增大摩擦系数会增大自复位节点的残余变形，但自复位节点的残余变形仍然很小，当摩擦系数为0.5时，残余变形仅为0.13%，自复位节点仍然具有较好的复位能力，因此增大摩擦系数能有效提高自复位节点的耗能能力。然而摩擦系数也不宜过大，否则会出现自复位节点无法复位和过早进入塑性的现象。

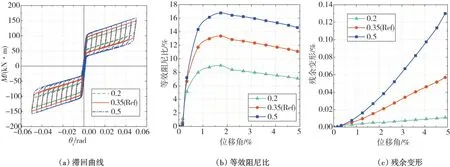
图11 摩擦系数对自复位节点力学性能的影响Fig.11 Effects of friction coefficients on mechanical properties of self-centering connection

3.5 弹簧刚度

碟簧装置的刚度主要取决于碟簧叠合数量和碟簧组合方式，本文分别考察了单片碟簧叠合、两片碟簧叠合和三片碟簧叠合，其他参数不变的情况下自复位节点的受力性能，碟簧装置的刚度分别为5.67 kN/mm、19.02 kN/mm和35.42 kN/mm。

由表2 和图12（a）可知：弹簧刚度对自复位节点开口后刚度和抗弯承载力的影响较大，但对节点开口弯矩和初始刚度的影响较小。开口之后，节点的刚度主要取决于碟簧装置，因此随着碟簧装置刚度的增加，节点开口之后的刚度也会随之增大。在加载后期，自复位节点开口后刚度出现了增大的趋势，以刚度为35.42 kN/mm 为例，当层间位移角为4%时，节点的开口后刚度开始出现增大的趋势。这是由于当层间位移角为4%时，碟簧的变形量在0.75h0左右，此时碟簧的刚度会明显增大，因此节点的开口后刚度会出现增大的趋势。

由表2可知：弹簧刚度从5.67 kN/mm 增加到19.02 kN/mm 时，等效阻尼比下降了47.8%，残余变形下降了36.8%；弹簧刚度从19.02 kN/mm 增加到35.42 kN/mm 时，等效阻尼比下降了40%，残余变形下降了8.3%。由图12（b）和图12（c）可知：弹簧刚度对自复位节点耗能能力和复位能力的影响较大。当弹簧刚度增大时，自复位节点的复位能力也会随之增大，但节点的耗能能力却随之下降。这意味着增大弹簧刚度能有效提高自复位节点的复位能力，但弹簧刚度也不宜过大，否则在加载后期会出现刚度不稳定的现象。

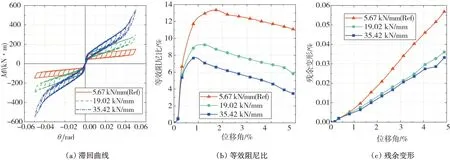
图12 弹簧刚度对自复位节点力学性能的影响Fig.12 Effects of spring stiffness on mechanical properties of self-centering connection

4 碟形弹簧自复位节点恢复力模型

由有限元分析结果可知：碟形弹簧自复位节点的滞回曲线呈典型的“双旗帜形”，符合自复位结构的基本特征。自复位节点的理论滞回曲线可分为4 个阶段，每个阶段所对应的刚度分别为k1、k2、k3和k4，如图13 所示。在第一阶段，梁端弯矩M小于节点的开口弯矩MIGO，梁柱之间不发生相对转动，此时，自复位节点可等效为传统的刚性节点，此时自复位节点的转动刚度k1为：

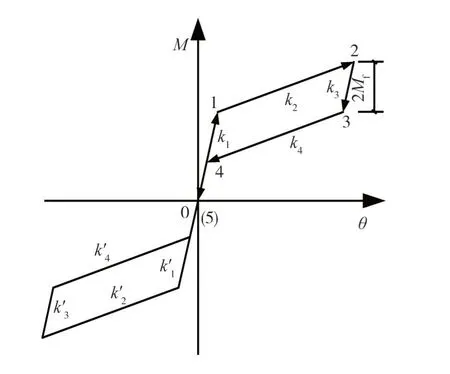
图13 理论滞回曲线Fig.13 Theoretical hysteretic response

式中：l为梁端加载点至转动中心的距离。

在第三阶段，自复位节点的变形主要来自于钢梁和钢柱的弹性变形，梁柱之间几乎不发生相对转动，因此第三阶段的刚度与第一阶段的刚度近似相等，即：

卸载到3点时，摩擦力矩被克服，自复位节点开始发生反向转动，因此3点的弯矩M3为：

在第四阶段，摩擦力矩被克服，摩擦耗能装置再次进入零刚度段，此阶段的刚度主要由碟簧装置决定，即：

卸载到4点时，自复位节点的开口闭合，碟簧装置恢复到初始状态，因此4点的弯矩M4为：

卸载到5点时，自复位节点恢复到初始状态。

将上述恢复力模型的理论计算结果与有限元计算结果进行对比，如图14 所示。由图可知：恢复力模型的理论计算结果与有限元计算结果基本吻合。在第三阶段，理论滞回曲线的刚度偏大，这是由于在推导恢复力模型时，假定其刚度与初始刚度近似相等所致。

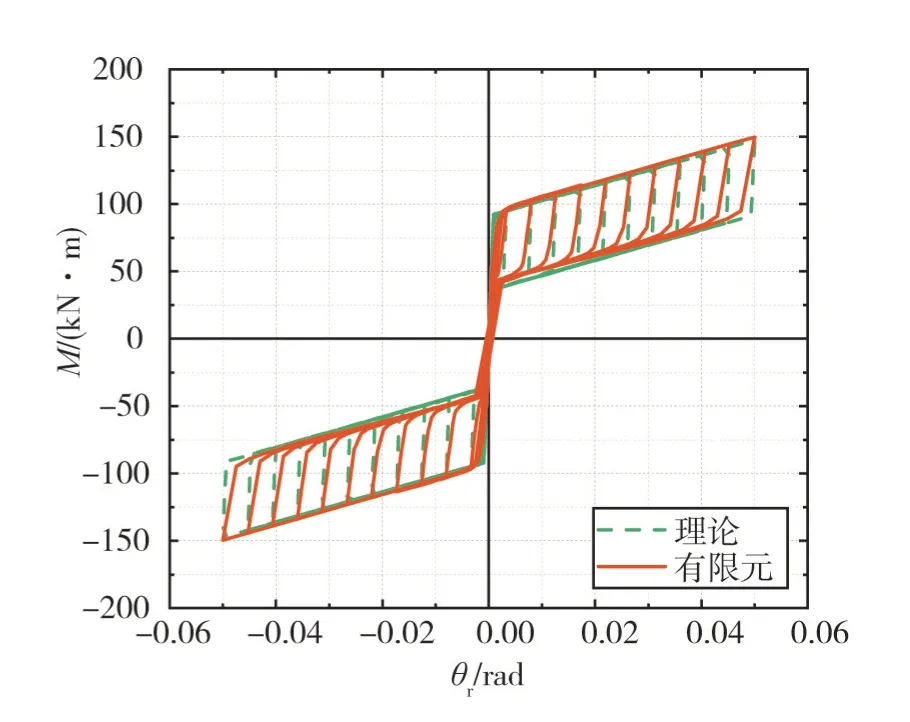
图14 恢复力模型理论结果与有限元结果对比Fig.14 Comparison between theoretical results and finite element results

5 结论

本文提出了一种新型碟形弹簧自复位梁柱钢节点，该节点的滞回曲线呈现典型的“双旗帜形”，具有较好的耗能能力和复位能力。通过对该节点受力性能的理论分析和数值模拟分析得到如下结论：

（1）增大腹板摩擦耗能装置的螺栓预紧力和摩擦系数能明显提高自复位节点的抗弯承载力和耗能能力，但螺栓预紧力和摩擦系数也不宜过大，避免自复位节点过早进入塑性。

（2）增大弹簧预压力能明显提高自复位节点的抗弯承载力和复位能力；弹簧预压力对节点的耗能能力没有显著影响。

（3）增大弹簧刚度能明显提高自复位节点开口后刚度、抗弯承载力和复位能力，但弹簧刚度也不宜过大，以确保自复位节点具有稳定的开口后刚度。

（4）推导了碟形弹簧自复位梁柱钢节点的恢复力模型，理论计算结果与有限元计算结果基本吻合。