碟形弹簧内锥角的计算

□ 季 乐 □ 彭 亮 □ 吴智科

南京三众弹性技术研究院有限公司 南京 210031

1 研究背景

碟形弹簧具有轴向空间紧凑、缓冲能力强的优点,在越来越多的领域获得了应用,在很多地方可以代替螺旋弹簧[1-3]。目前,对碟形弹簧的研究主要集中在力学特性,以及缓冲减振、控制运动的应用上[4-8]。但是,对于碟形弹簧几何特征中的内锥角,精确计算一直未见报道,常见的计算方法均为近似值[9-10]。对此,笔者提出一种计算碟形弹簧内锥角的方法。

2 碟形弹簧几何尺寸

给定碟形弹簧的外径D、内径d、厚度t、高度H0,即可确定碟簧尺寸,如图1所示。内锥角为α。

图1 碟形弹簧尺寸

3 普通碟形弹簧内锥角计算

由图1可得如下关系:

(1)

整理后可得:

(D-d)/2×sinα-tsin2α=H0cosα-tcos2α

(2)

令x=sinα,于是有:

(3)

整理后得到:

(4)

可见,这是一个一元四次方程,可用牛顿迭代法求解,记:

y=Ax4+Bx3+Cx2+Ex+F

(5)

式中:A、B、C、E、F为对应项的因数。

其导函数为:

y′=4Ax3+3Bx2+2Cx+E

(6)

(7)

(8)

一般经三次迭代,即可获得满意精度,内锥角为:

α=arcsin(x3)

(9)

例一:某碟形弹簧的外径为31.5 mm,内径为16.3 mm,厚度为1.75 mm,高度为2.45 mm,求这一碟形弹簧的内锥角。

初值为:

进行迭代,见表1。

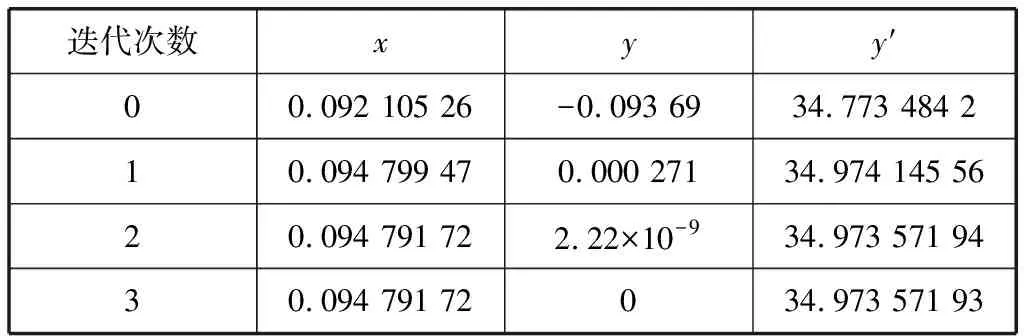
表1 例一内锥角计算迭代

则内锥角为:

α=arcsin(x3)=arcsin 0.094 791 72

=0.094 934 26 rad

换算成角度制,α为5.439 33°。

以上计算过程可编辑成Excel表格,省时便捷。

例二:在AutoCAD软件中绘制例一所述碟形弹簧的截面。

由于AutoCAD软件稍早一些的版本无法自约束尺寸,因此需借助上面计算出的内锥角进行绘图。

从任一点M引一条角度为5.439 33°的直线MN,往下绘制一条与之平行,且距离为1.75 mm的直线PQ,在上方绘制一条距离点P为2.45 mm的水平线P′N,与直线MN交于点N。绘制直线NQ垂直于直线PQ。删除多余线段,并制作镜像,即为所得,如图2所示。可见,测量的数据与碟形弹簧尺寸相同。

图2 例一碟形弹簧绘制

4 带圆角的计算

实际生产的碟形弹簧,截面的四个角是圆弧过渡的,圆弧半径为r,尺寸如图3所示。

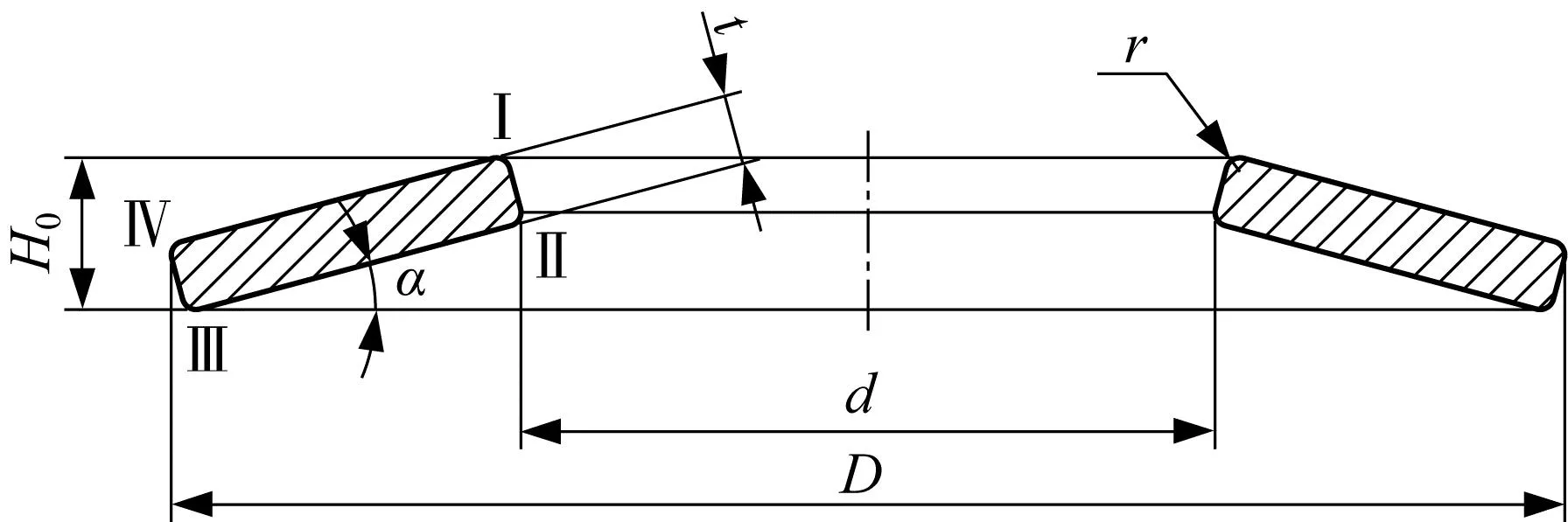
图3 带圆角碟形弹簧尺寸

考虑截面去除圆角后的中间矩形部分,矩形部分的内锥角与原碟形弹簧相同,如图4所示。由此,只要在式(4)中将D、d、t、H0依次以D-2r、d+2r、t-2r、H0-2r代替即可。

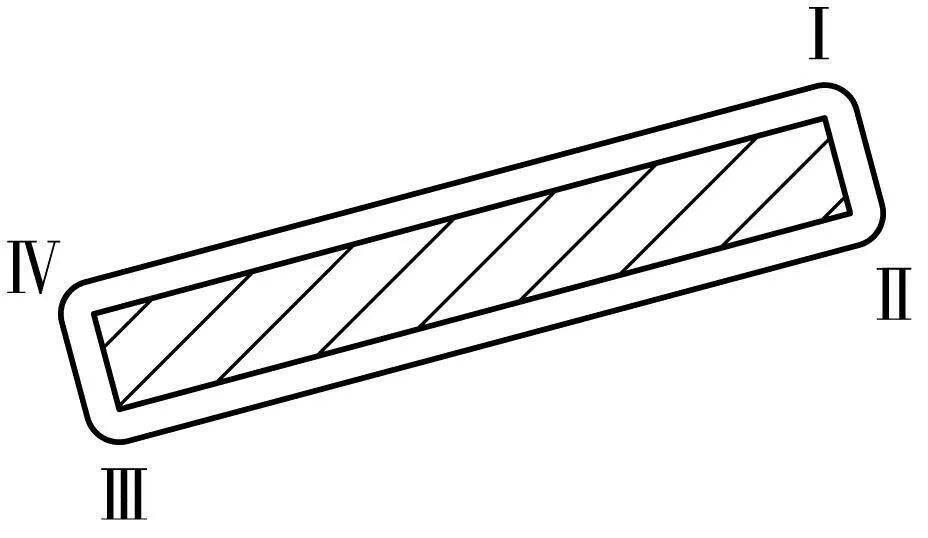
图4 中间矩形部分内锥角

5 有支撑面的计算

有支撑面的碟形弹簧尺寸如图5所示,b为支撑面宽度,t′为厚度。

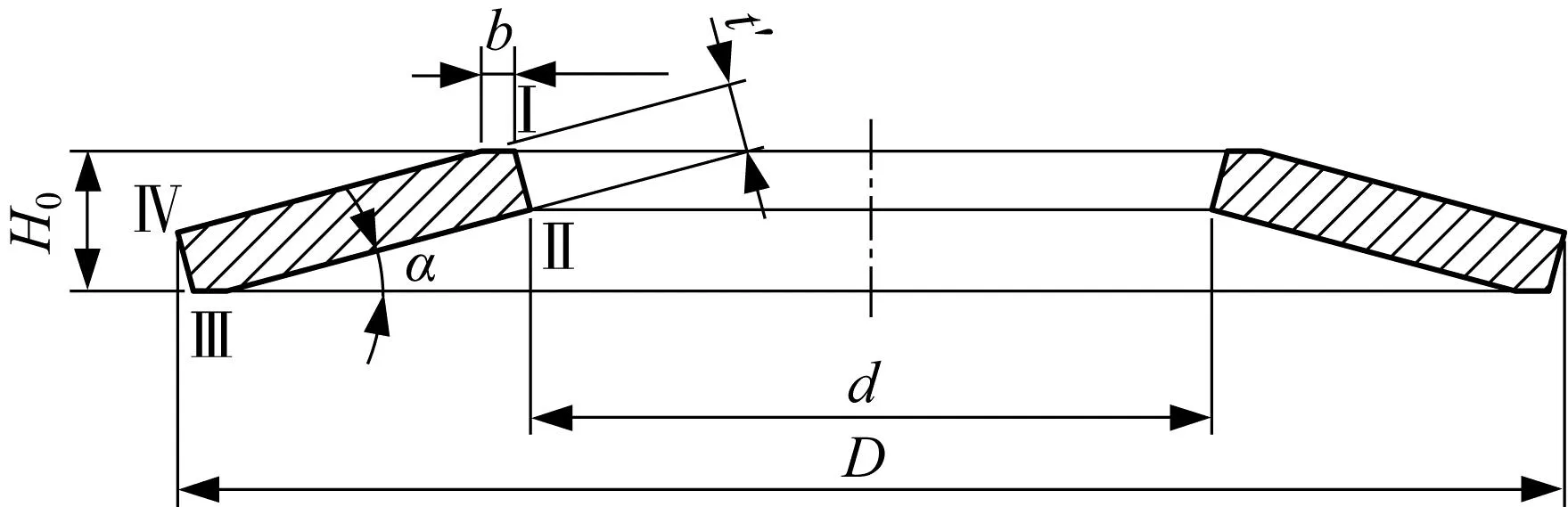
图5 有支撑面碟形弹簧尺寸

与无支撑面碟形弹簧类似,由图5可得如下关系:

(D/2-d/2-t′sinα-2bcos2α)tanα=

H0-t′cosα

(10)

整理后得:

(D-d)/2×sinα-t′sin2α-2bsinαcos2α=

H0cosα-t′cos2α

(11)

令x=sinα,可得:

(D-d)/2×x-t′x2-2bx(1-x2)=

(12)

整理得一元六次方程:

Ax6+Bx5+Cx4+Ex3+Fx2+Gx+H=0

(13)

A=4b2

(14)

B=-8bt′

(15)

C=4t′2+4[(D-d)/2-2b]b

(16)

E=4bt′-4[(D-d)/2-2b]t′

(17)

(18)

G=2[(D-d)/2-2b]t′

(19)

(20)

也可用牛顿迭代法计算出带支撑面碟形弹簧的内锥角,记:

y=Ax6+Bx5+Cx4+Ex3+Fx2+Gx+H

(21)

其导函数为:

y′=6Ax5+5Bx4+4Cx3+3Ex2+2Fx+G

(22)

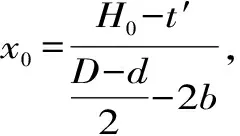
一般经三次迭代,即可获得满意精度,内锥角为:

α=arcsin(x3)

例三:碟形弹簧外径为250 mm,内径为127 mm,厚度为6.7 mm,高度为14.8 mm,支撑面宽度为1.75 mm,求内锥角。

初值为:

进行迭代,见表2。

表2 例三内锥角计算迭代

则内锥角为:

α=arcsin(x3)=arcsin 0.141 543 66

= 0.142 020 602 rad

换算成角度制,α为8.137 181°。

以上计算过程可编辑成Excel表格,省时便捷。

6 带圆角有支撑面的计算

带圆角有支撑面碟形弹簧的尺寸如图6所示。

图6 带圆角有支撑面碟形弹簧尺寸

对此,可将圆角补齐为直角,如图7所示。

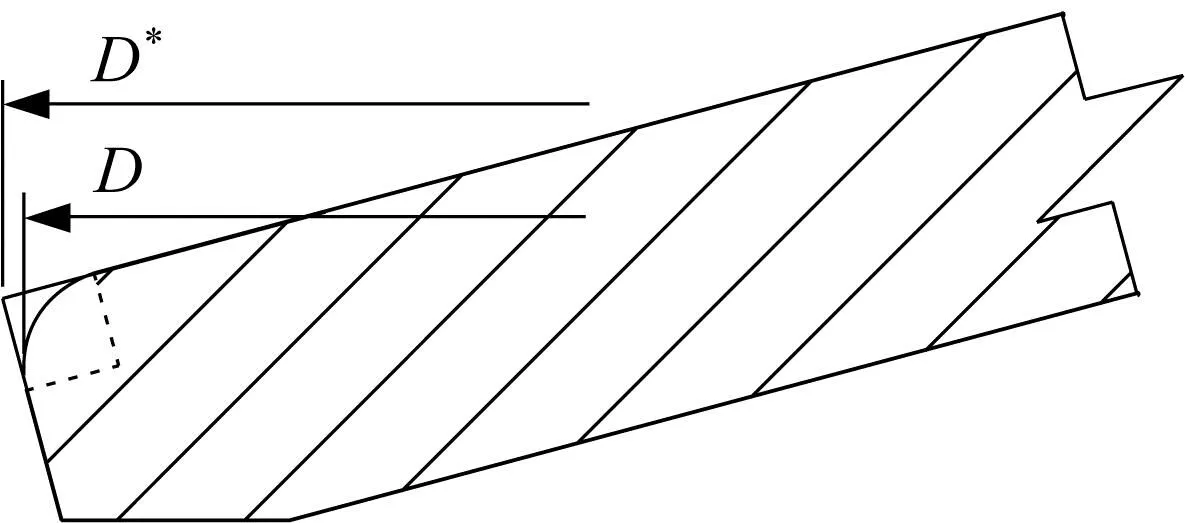
图7 圆角补齐

对内外径进行修正,可得:

D*=D+2r(sinx0+cosx0-1)

(23)

d*=d-2r(sinx0+cosx0-1)

(24)

然后在式(16)～式(19)中,用D*、d*代替D、d即可。

由于D*、d*的计算用的是初值x0,因此最终计算的内锥角会有些许误差。

7 结束语

笔者针对普通碟形弹簧、带圆角碟形弹簧、有支撑面碟形弹簧、带圆角有支撑面碟形弹簧,分别推导内锥角计算式,并给出计算示例与应用,具有参考价值。