基于稀疏表示的数控机床主轴故障特征提取*
□ 黄日进 □ 李成贵 □ 邹才深
广西英华国际职业学院 广西钦州 530213
1 研究背景
数控机床作为典型的机械设备,在工业生产中被广泛运用。对机械设备的运行状态进行监测,是一种发现早期故障,避免生产损失的常见手段。数控机床的主轴振动信号能够反映设备运行状态,是一种故障监测预警的理想对象[1-2]。不过,由于噪声干扰、频率混叠及早期振动不明显等广泛存在的问题,对故障信号进行分析存在一系列难点。稀疏表示理论近年来在信号分析领域被广泛关注和尝试,具有从冗余数据中选择提取有效信息的能力,为从复杂信号中挖掘故障核心特征提供了一种新的路线。
对信号进行稀疏表示,在稀疏优化目标函数的约束下,从包含信号信息的过完备原子库中选取有限个原子作为信号特征提取结果。王林等[3]将稀疏表示理论运用于滚动轴承故障特征提取,并选取匹配追踪算法作为稀疏系数的求解方法。石娟娟等[4]提出一种基于优化最小的稀疏表示方法,用于提取和分离齿轮箱齿轮复合故障特征成分。孟宗等[5]研究滚动轴承瞬态冲击信号的稀疏表示方法,实现对轴承故障类型的有效鉴别。
数控机床在运转中,主轴会产生非平稳故障振动信号,具有时变特性,导致难以有效在时域中捕捉并分析特征。作为一种旋转机械,主轴频域信息较之时域对故障有更好的可解释性[6]。笔者提出一种基于稀疏表示的数控机床主轴故障特征提取方法。首先在信号的希尔伯特-黄变换边际谱上,以信号的瞬时频率信息构建过完备解析字典。然后引入稀疏主成分分析算法,对信号的字典载荷进行稀疏求解,将主分量对应的特征频率作为能够反映不同故障主要差异的稀疏基,来构建原始故障信号的稀疏表示。最后建立仿真数据集,对模型有效性进行验证分析。
2 故障信号稀疏表示
2.1 过完备字典
数控机床主轴机械故障会引起一组具有特定频率的异常振动,利用全频谱分析方法对信号进行频域分析,可以获得系统的固有频率和故障的特征频率等信息[7-8]。在噪声及继发故障等复杂工况的干扰下,数控机床主轴振动信号会表达出非周期非平稳特性。为此,对振动信号的时域波形s(t)进行希尔伯特-黄变换,求取信号的时频域信息h(ω,t),为:
h(ω,t)=H[s(t)]
(1)
式中:H代表希尔伯特-黄变换函数;ω为角速度;t为时间。
对时域积分,得到故障信号的瞬时频率表达,为:
(2)
式(2)即希尔伯特-黄变换边际谱。
构造一个n维状态空间Rn,对于一个给定的故障信号si(t),令其对应状态向量xi为:
xi=[xi1xi2…xin]xi∈Rn
(3)
xij=hi(ω)|ω=ωjj=1,2,…,n
(4)
式(3)对应希尔伯特-黄变换边际谱hi(ω)上的n点采样。由于频率混叠等原因,相邻频率之间是非正交的,整体信息存在冗余,所以式(3)成为表示给定故障信号的一组过完备字典。
2.2 稀疏系数矩阵
根据式(3),将m个采样信号在希尔伯特-黄变换边际谱上的采样值构建为样本的非稀疏系数矩阵X,为:

(5)
对X进行奇异值分解,为:
X=UΣVT
(6)
式中:U、V分别为m×m和n×n正交矩阵;Σ为对角矩阵。
Σ对角元素为从大到小排列的X的非零奇异值,V的各列就是Σ中非零奇异值对应的特征向量。
记Vj为V的第j列,令:
Fj=XVj
(7)
式中:Fj为第j个主成分的非稀疏初始赋值。
以如下所述的回归分析形式继续进行稀疏化求解[9],为:
(8)
式(8)对应稀疏主分量的优化问题,表示在稀疏度测量函数l2范数下求取最小方差,β为求取第j个稀疏主成分的载荷向量。
添加β的l2范数惩罚项,避免在高噪声环境下对模型过度拟合。此外,根据文献[10]提出的稀疏主成分分析算法,通过添加β的l1范数惩罚项,实现对载荷向量的稀疏化,最终得到目标函数,为:
(9)
式中:λ、λ1为动态调整的惩罚项因数。
当λ1足够大时,可以得到稀疏的β。重复式(7)~式(9),计算其它稀疏主成分,进而可以得到一个低维空间的稀疏状态向量,作为原始故障信号的稀疏表示。
3 仿真验证分析
3.1 主轴振动模型
数控机床主轴作为一种旋转机械,不同类型故障各自对应一种或多种特征频率。根据正常工况、主轴不平衡、主轴不对中、切削刀具摩擦的物理模型特性,对四类工况按照下述公式设定仿真信号[11],为:
s1(t)=A1sin(2πft)
(10)
s2(t)=A1sin(2πft)+A2sin(2πft+φ)
(11)
s3(t)=A1sin(2πft)+A3sin(2π2ft)+A4sin(2π4ft)
+A5sin(2π8ft)
(12)
s4(t)=A1sin(2πft)+A6sinc(2πft)
(13)
s1代表正常工况,刻画系统本身的工作频率。s2代表主轴不平衡故障,包含系统工频和一组同频异相的异常振动。s3代表主轴不对中,除系统工频外,在二倍频、四倍频、八倍频加入幅值依次减小的异常振动。s4代表切削刀具摩擦,利用sinc函数模拟快速衰减的冲击信号成分。
令f为10 Hz,A1~A6分别为1、2、2、1、0.3、1,φ为π/2,并对所有信号添加信噪比为3 dB的高斯白噪声,记录5 s的时域波形,最终得到四种条件下数控机床主轴振动仿真信号样本,如图1所示。
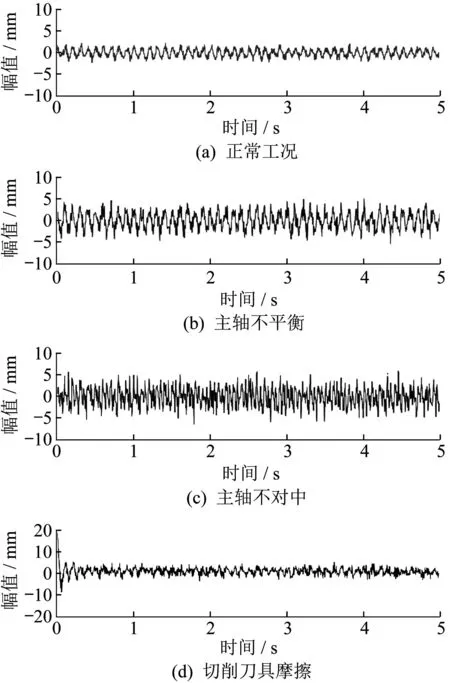
图1 振动仿真信号样本
根据式(2),求解仿真信号的希尔伯特-黄变换边际谱,如图2所示。观察到相比于正常状态,主轴不平衡和切削刀具摩擦故障都出现了低于工频的异常频率,高频部分则均无明显能量。在衰减冲击信号的影响下,出现切削刀具摩擦故障的信号在低于工频部分有更明显的能量。主轴不对中故障展现出相比其它情况更宽的故障频带。
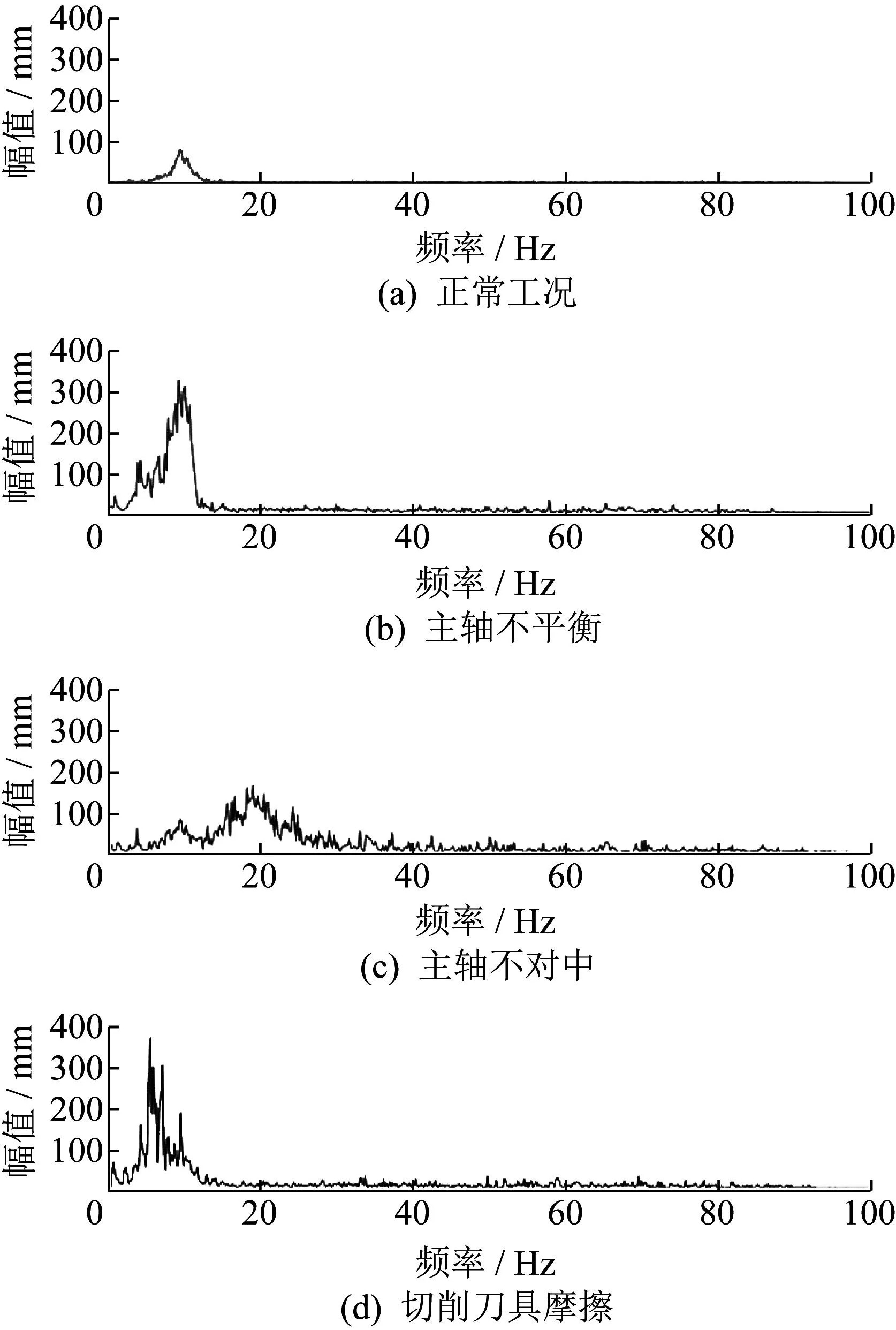
图2 仿真信号样本希尔伯特-黄变换边际谱
3.2 故障信号稀疏表示
在每种条件下重复生成50组信号,共计得到200组信号,作为主轴振动仿真信号数据集。对信号在希尔伯特-黄变换边际谱进行500个点的均匀采样,构建非稀疏系数矩阵。利用稀疏主成分分析算法进行稀疏化求解,得到给定仿真信号数据集的主分量对应的特征频率,见表1。

表1 主分量对应特征频率 Hz
主分量1~主分量5的权重依次降低,其中主分量1反映了系统中可能出现的非周期冲击信号扰动,主分量2为系统的正常工频,主分量3体现了故障振动中能量最大的二倍频成分。选取前三个主分量计算仿真信号数据集的状态空间向量,得到200组仿真信号在三维空间中的关系,如图3所示。可以看到,主分量1~主分量3已能对给定信号按照不同工况条件进行较为有效的区分。

图3 仿真信号三维空间关系
4 结束语
笔者将稀疏理论与信号分析结合,以数控机床主轴振动信号为研究对象,提出一种基于稀疏表示的数控机床主轴故障特征提取建模方法。振动信号的希尔伯特-黄变换边际谱刻画了信号的瞬时频率特性,能有效捕捉机械故障引起的非平稳振动。在希尔伯特-黄变换边际谱上构建信号的过完备表示,根据稀疏主成分分析算法,选取能反映不同工况信号主要差异的特征频率来构建信号的状态空间向量,作为信号的稀疏表示。
经过仿真数据分析,这一方法能有效捕捉系统的工频、能量最大的倍频、快速衰减的冲击信号等成分,实现对主轴不平衡、主轴不对中、切削刀具摩擦等故障信号的特征提取和分类。

