计算思维的浓度

陈凯 上海市位育中学

考虑这样一个简单的任务：有某个列表，规定其中所存储的数据处于非1即0的两种状态之一，要求学生按枚举的方式编写算法，将列表中存储状态取反，也即将所有的1变为0，将所有的0变为1。请问，学生在任务实施过程中，有没有运用到计算思维？又凭什么理由说有或者没有运用到计算思维呢？后一个问题显然更难以回答。因为教师可能有这样的感觉：在此任务的实施过程中无论如何都可能涉及一些计算思维的运用，但若想进一步解释哪里涉及了计算思维的运用，却又难以言说了。那么，不妨换个角度加以询问：学生在何种情况下实施这个任务以及怎样实施任务，能更好地体现出计算思维的运用？举例说，有以下几种情况。情况A：学生已经学习过在列表中查询所有的奇数并打印的算法和程序代码，要求学生将已学习过的算法和程序代码稍加改造，用于新布置的状态取反任务；情况B：学生已经学习过在列表中查询所有的奇数并打印的算法和程序代码，要求学生利用陌生的积木式图形编程环境编写算法来实现状态取反任务；情况C：学生已经学习过在列表中查询所有的奇数并打印的算法和程序代码，此时被要求在了解了一定的图灵机的规则后，按图灵机的运行方式编写算法来实现状态取反任务。对于以上三种情况，教师们可能有一种朦胧的感觉，似乎情况B和情况C的任务实施过程，对计算思维的要求更高。在这里，笔者试着借用“浓度”一词，来描述任务中对计算思维方面能力的要求的程度。当然，对于具体任务的差异与计算思维浓度的关系，是否能在一定程度上取得共识，尚需要在较大规模的调查后方能得到结论。本文聚焦的是另一个问题，即教师直观上会对任务实施产生出计算思维浓度差异的感觉，其根本原因是什么？围绕这个问题，本文给出若干假设，可作为深入调查研究的线索，值得在实际的教学工作中加以验证。提出这些假设的目的是解答这样的疑惑：在某特定任务的实施中，模式识别、解构和抽象等思维的运用，是如何上升为具有计算机科学特征的计算思维的？

●模式的挖掘

设想一下，几乎每个人在用数字计数的时候，其行为都是自然而然的，在计数过程中，头脑不会明显意识到逢十进位的规则。而一些对二进制已经非常熟悉的人，他们在计数时，也同样会感觉到二进制数码的变化过程是自然而然的，也许只有当被问及是如何知道每次增加1之后数码的变化，大概才会隐约感觉到计数过程中各个数码所发生的类似于套娃一般的变化规律。人的头脑在把握二进制计数过程中对数码变化的感觉，与在古老的九连环拆装过程中所体验到的有相当程度的类似。而初学二进制的人则更有可能根据逢二进一的规则，用逻辑来推导出数码的变化。对于已经相当熟悉十进制或二进制计数的人来说，若要制作出一个能够计数的装置，那么更重要的，恐怕不只是识别出某种模式，而是要挖掘出某种模式，前者是人的头脑自然而然的行为，后者是人用某种机械化的方式对原本自然而然的行为进行模拟。以二进制计数为例，可能被挖掘出来的模式是多样的。例如，可以由每个数码相互影响的连锁反应来挖掘出某种规律：经观察可知，每一次加1，最后一个数码的状态总是取反，而只有当数码的状态由1转而为0时，它左侧也就是高位的数码状态才取反，这个连锁反应可以一直向更高位传递下去；或者，也可以从加1的频率和数码的状态之间挖掘出规律（数码之间的相互影响反而是可以忽略的），可以注意到，每次加1，最后一个数码状态总是取反，而每次加2，高位的数码状态总是取反，每次加4，更高位的数码状态总是取反，以此类推。当然，存在更多可能被挖掘出的变化模式，如采用特定的递归或迭代的算法都可以实现二进制计数的数码变化，而这些规律对于数码变化过程实施的效果，都与二进制计数逢二进一的数学规则实施的效果是一致的。变化模式的多样性，为计算的机械化实现提供了多种多样的可能。

这里给出另一个例子，假设有一串数字为1、121、12321、1234321，如问下一个数字会是多少，显然应该是123454321，为后续行文方便，不妨称其为金字塔计数。每个人都不妨回想一下，自己是如何在头脑中按当前模式变换出下一个数字的。以下是某一种常见的思维模式的示例，当在头脑中念出121的时候，“2”这个数字在心中留下了特别深刻的印象，从而为下一轮的变化做好了铺垫，相对地，从1到2的变化，以及从2到1的变化，反而是自然而然进行的。于是，在下一轮念数的一开始，头脑就先将2转变为3，然后自然而然地从1计数到3，并同时对“3”这个数字进行了特别加深的记忆，以便为下一轮变化做好铺垫……这可能是人的头脑在金字塔计数中实现模式识别的最好方法了。若是编写某个算法，主要以模拟人的思维过程的方式来实现金字塔计数当然是可以的，不过显然，存在更多种实现此类变换的方式。下面给出两种不同的方法：比如，对列表[0，0，0，0，1，0，0，0，0]中的数据进行迭代，将所有存在着的非0的数字，以及虽然是0但旁边是1的数据加1，显然，借助简单的枚举算法就可以将列表变换为[0，0，0，1，2，1，0，0，0]，若再进行一次替换列表就变成[0，0，1，2，3，2，1，0，0]，以此类推。或者也可以考虑采用分形的方式来实现变换，假设用“*”符号的数量来表示某个数字，那么，如允许在变换过程中引入某些临时的符号，就可以设计一套特定的规则进行符号的替代变换并实现金字塔计数。一种可行的方案是这样的，初始符号串为“<*.>”，其中“.”为数字之间的分割，“<”和“>”代表数字的边界，接下来只要反复实施将“*.”变为“**.”、将“<”变为“<*.”、将“>”变为“*.>”的替换，就能实现本节金字塔计数任务了。由这些例子可以看出，计算思维中的模式识别，更多具有挖掘隐含规律的意味。

无论是机械化的二进制计数，还是分形式的金字塔计数，可以看出，它们在实现过程中的变化模式与人日常思维的模式都有很大的差别，所以，当任务的目标确定为实现某个自动计算的装置或算法时，可以借由观察这种思维方式上的差异，来估计计算思维的浓度。

●局部构件对整体行为的模拟

假设学生将要实施的任务是：判断某个数字的奇偶性，如果是奇数，则对该数乘以3再加1，如果是偶数，则对该数除以2。很容易用流程图描述算法，在流程图中可以看到有判断数字奇偶性的判断框,有数字乘以3加1的处理框，有数字除以2的处理框等。假设将这个流程图的各个部分拆成零件，然后将这些零件交给另一个人，并向其告知整个任务的目的，那么此人应当较为容易推测出，由流程图拆为零件的各个部分在功能上的意图。

不过，在某些时候，局部的构件的行为，只有放在整体的视野下才具有意义。例如，利用计数频率和二进制数码的状态的关系设计如下计数方法。步骤1：写八个0和八个1放置在一行；步骤2：再写两遍四个0和四个1放置在下一行；步骤3：再写四遍两个0和两个1放置在下一行；步骤4：再写八遍一个0和一个1放置在下一行。其过程如下页图1所示。被拆解出来的前三个步骤似乎与二进制计数的功能是无关的，只有在实施最后一步时，才能领会到，所有的步骤与二进制计数有着整体上的联系，从而产生出从纵向上看数字的变化正对应着二进制计数的效果。

图1 注：只有在步骤4实施过程中，才能实现计数，并显现出前面步骤的意义

这里再举一个例子。考虑这样的情况，某个二进制运算装置并不以“0”作为“0”，以“1”作为“1”，而是以信号出现位置作为判别数值的依据。例如，下页表中的数据表示的是二进制数“0111”。看上去就好像有个拨码开关，往上拨为“1”，往下拨为“0”。这里姑且称之为拨码二进制。

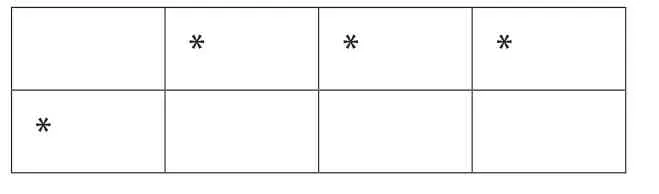
用信号的位置表示二进制数值

怎样用这样的装置来进行计数呢？一种可行的程序代码和运行效果如图2所示。和上面的例子类似的是，从代码中也很难直接看出逢二进一的数学规则。

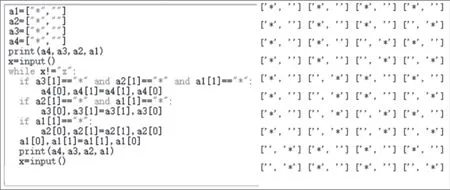
图2 一种二进制计数的方法

从上述例子可以看出，一个自动化过程或装置的解构和构造，常常具有复杂系统中层级模拟和功能涌现的特点，这个特点有时会因为高度的模块化封装而被遮蔽起来。例如，用Python语句来实现两个数字相加的运算，简单的一句print(a+b)就能实现，但何以能实现这个功能？即便深入到两个数字的相加是如何用底层机器指令描述的，人们还是无法知晓机器到底是怎样实现加法操作的，只有将指令和硬件电路当作一个整体来了解时，才能领悟到运算器、控制器、存储器三者在实现任务时错综复杂的关系和此计算何以可行在整体上的原因，这种领悟无疑需要更多更强的计算思维能力。笔者并不是想说，教师们一定要在教学中解释计算机底层工作的原理，而是想说，仅仅用超级简略的五大逻辑部件的计算机架构图纸或者十来行实现某简单任务的程序代码来当作教学内容，并宣称能实现计算思维的培养，这是相当可疑的。

●可实体化的抽象

计算思维中的抽象与数学上的抽象有怎样的区别？数学上的抽象保留了量的关系和空间形式，而舍弃了非数学的一切特征，往往有着抽象概念逐级提高的特点。而一个计算装置为了真正制造上的可能性，有对抽象之物实体化的特点，并且，计算装置中的实体化，既有为了实现更广泛的他物的需求而升级的趋势，也有为了实现自身而寻求基础元件的降级的趋势。下面用一个用数字逻辑实现的二进制加法的装置来具体说明，图3所示是一个二进制加法模块处理两个输入数据，并得到两个输出数据的演示。

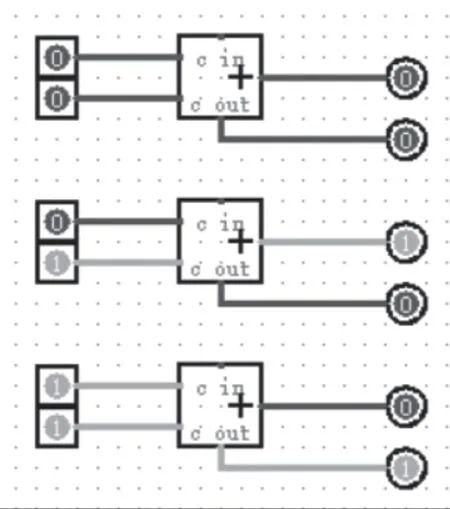
图3 二进制加法输入和输出的三种情况

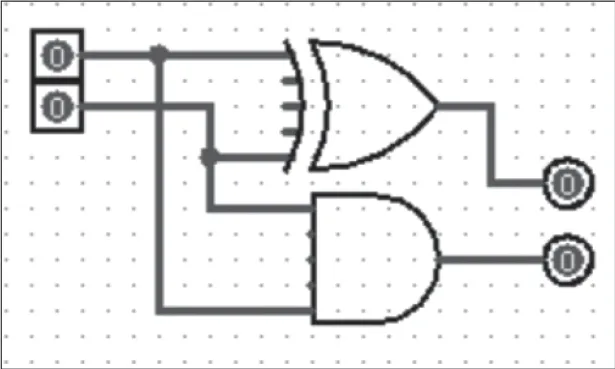
图4 实现两个二进制数字加法的半加器

将加法器模块分解成两个逻辑门后，可发现这两个逻辑门本身仍然是抽象的概念，还可以继续向更底层寻得使其能具有逻辑运算能力的更基础的元件，那就是三极管。三极管仍然是抽象的概念，直到寻得物理上的实体的晶体管或电子管。

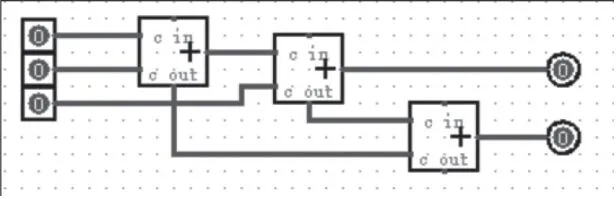
图5 实现三个二进制数字加法的装置

如果使用前面所说的拨码二进制的形式组装一个二进制加法器，结构就完全不同了。图6所示是一个可对两个二进制拨码进行加法运算的装置。

图6 一种拨码二进制加法装置

以上所举的数字电路的例子主要是用来说明，每一种抽象的功能元件，用以实现其功能的基础实体是多样的；而每一个作为基础的实体元件，用于构建整体功能的方式也是多样的。一个朴素的假设是，计算思维能力较强者，能更灵活地依赖抽象元件的实体化的多样性来解决问题。

●提升计算思维的浓度

本文从模式识别、解构、抽象三个角度给出了关于计算思维浓度的假设，认为某个任务若对计算思维能力有较高的要求，需要实施者对模式的挖掘、局部构件对整体行为的模拟、可实体化的抽象这三点有所作为。

考虑这样一个任务，即编写算法计算第n项斐波那契数列项的值。比较容易想到的方法是，设立某列表，列表的第一项和第二项都存入数字1，借助循环语句使列表之后每一项都是前两项之和。如果试着将算法的行为实体化，就可以想象出这样的画面：某个机器跨骑在列表第一项和第二项的位置上，它通过两个信号读取传感器读入列表两个项的值，机器将两个值相加，然后向右移动列表一项的位置，当机器跨骑在第二项和第三项的位置时，将先前加法运算的结果写在列表第三项的位置上，接下来，就是读入第二项和第三项的值，以此类推……这种实体化的想象是多样性的，也可以想象同时有许多机器都跨骑着三个列表项，每个机器都可以将左面两个列表项的值相加存入最右面的列表项，这其实就用到多引擎计算的思路了，其实施步骤与前者有相当大的区别。在放开束缚进行实体化的想象时，须知这里所说的实体不一定是真正物理意义上的实体，如在用递归的方法计算斐波那契数列项的相关想象中，机器本身具有瞬间自我复制的能力。从培养计算思维角度看，在设计特定算法计算斐波那契数列项的时候，希望学生领悟到自己其实是在用一个现实世界中可能不存在的物件来实施某个计算任务，当然，这种可能不存在的物件在抽象的概念上是成立的，它自身是由更基础的现实中可能存在的物件、或仍然可能不存在的物件模拟出来的。

除了无束缚地对抽象物件进行实体化可能性的想象，有时也可以经由特定的实体化的限制来启发思维。假设这样一个任务：只用一个存储空间来存储斐波那契数列项的数据，并计算第n项的斐波那契数列项的值。一种可能的方法是，将变量值设为形如“101”的样子，其中“0”之前“1”的数量代表第一项的值，“0”之后“1”的数量代表第二项的值。于是，任务就转换成了如何将“101”变换成“1011”，继而变换成“110111”。显然，为了实现这种变换，就需要进一步挖掘出符号串变换的模式，然后用特定的算法来实施整个演化过程，从而模拟出斐波那契数列项的计算过程。

本文给出了一系列与模式识别、解构与抽象有关但又与日常思维中的模式识别、解构与抽象有一定区别的任务，并相信此类任务的实施需要较高的计算思维的浓度，但对于这个假设的科学论证，无疑还需要投入更多的时间、精力和资源。