函数单调性的四应用

李 柳

(河北省石家庄市第四十二中学)

函数问题历来是高中数学的重点与难点,说它是重点,因为它是高中数学大厦的基石,在高中数学的任何一个知识板块中都有函数；说它是难点,主要是因为函数性质的应用具有一定的综合性与灵活性.函数的单调性作为函数的基本性质之一,在数学解题中有着广泛的应用,那么灵活应用函数的单调性,能解决哪些问题呢?

1 利用函数的单调性比大小

2 利用函数的单调性解不等式

3 利用函数的单调性求值域或最值

4 利用函数的单调性求参数的值或范围

在函数单调性的应用中,常常出现一类含参数问题,要求解题者根据题中给出的单调性求参数的值或取值范围.

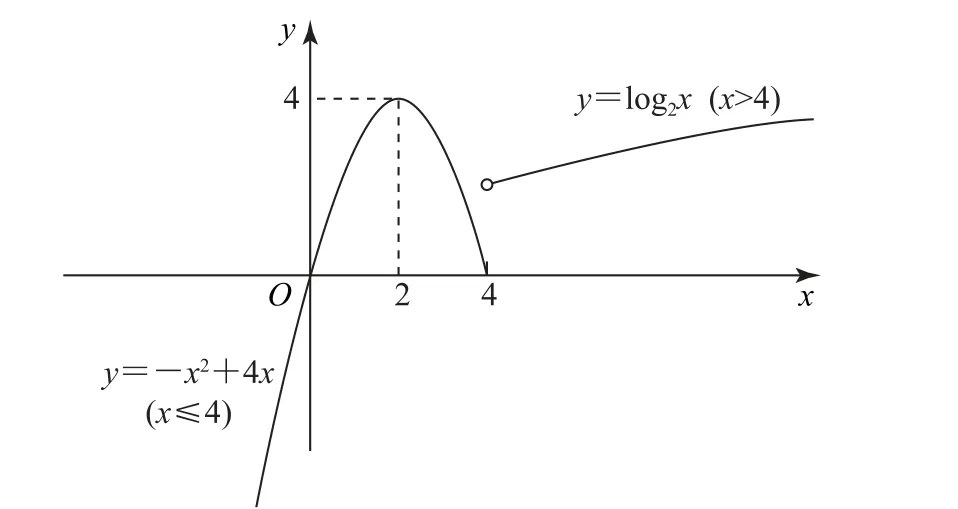
图1

基本初等函数的单调性一般取决于该函数的基本量,如指数函数与对数函数取决于它们的底数,幂函数则取决于它的指数,而分段函数则必须满足每一段单调,且整个函数单调.利用函数的单调性求参数的值或范围,一般转化为含参不等式组来处理,有时利用它的图像能更加直观地得到答案.

当然,函数单调性的应用远不止本文所提及的四种情形,如利用函数的单调性还可以解方程、作函数图像等.但无论是哪种问题,都离不开函数单调性定义的直接应用与逆向应用,有时还可辅以函数图像来分析问题,从而能更直观、更有效地得出答案.