借助函数的性质巧解题

和黎明

(山西省长治市长子县第一中学校)

函数的性质是高考考查的重点,特别是指数函数、对数函数、幂函数的基本性质,一般以选择题或填空题的形式出现,难度中等.本文结合例题对常见有关函数的性质问题进行分析,希望对学生的学习有所帮助.

1 借助函数的奇偶性,巧求值

归纳总结 求解此类问题需要关注以下两点:一是分析相关函数的奇偶性,具体问题中,往往需要灵活构造函数,并分析该函数的奇偶性；二是活用函数的奇偶性解题,灵活运用函数的奇偶性对目标式进行变形,再化简求值.

2 借助函数的单调性,巧求参数的取值范围

利用函数的单调性求参数的取值范围是一类经常考查的热点问题,只有熟练掌握指数函数、对数函数、幂函数的单调性以及复合函数的单调性法则,才能顺利求解相关问题.

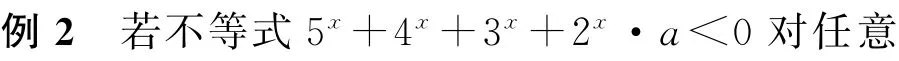
归纳总结 求解此类问题需要关注以下两点:一是分析函数单调性,具体问题中往往需要结合题意先构造函数,再分析其单调性；二是运用单调性,结合目标问题灵活运用得到的新函数的单调性加以求解.

3 借助函数的奇偶性和单调性,巧求参数的取值范围

求解与函数有关的不等式问题时,往往需要灵活运用函数的奇偶性,先对已知不等式(或目标不等式)进行适当变形,再利用函数的单调性加以求解.

归纳总结 求解本题的关键在于,先充分利用f(x)为偶函数这一条件对已知不等式进行化简、变形,再利用f(x)在区间[0,＋∞)上单调递减解不等式.特别提醒:一般地,若f(x)为偶函数,则必有f(x)＝f(|x|).

4 借助函数的对称性,巧求值

5 借助函数的性质,比较大小

归纳总结 上述求解思路可概括为借助设元变形,先将目标问题等价转化为考查2k－1,3k－1,5k－1的大小,再根据幂函数f(x)＝xk－1的单调性加以讨论分析.特别提醒:幂函数y＝xα在(0,＋∞)上的单调性可分为三种情况.

1)若α＞0,则函数单调递增；

2)若α＝0,则函数无单调性(为常数函数)；

3)若α＜0,则函数单调递减.

总之,处理与函数有关的数学问题,往往需要关注函数的单调性、奇偶性、对称性等,从函数的性质出发,探求具体的解题思路,提升解题能力.