基于PCA 和KPCA 的高光谱遥感数据降维对比研究

李昌元，刘国栋，谭 博

（1. 重庆交通大学土木工程学院，重庆 400074）

高光谱遥感影像在反映地物空间位置信息的同时也记录着地物反射的光谱波段信息，两种图像信息相互结合，能更精细地表现光谱维中不同地物间的细微差异[1]，大幅提升地物的识别与分类精度。然而，高光谱遥感影像数据光谱波段众多、特征空间维数过高，极易造成数据冗余，且光谱相邻波段间存在较强的相关性，更会引发“维度灾难”[2]，给后续的地物识别与分类等带来诸多困难。对高光谱遥感影像数据进行降维，既能充分利用其丰富的数据量，又能降低数据处理代价、解决特征空间维数过高的问题，还能保留必要的地物信息，提高地物识别、分类的精度和效率。

高光谱遥感影像数据的降维技术主要包括波段选择和波段提取两种，按照不同的标准又可分为线性映射和非线性映射降维[2]。基于线性变换降维的方法称为线性映射降维，主要包括PCA[3]、线性判别分析（LDA）[4]和独立成分分析（ICA）[5]等，方法简便且计算速度快。高光谱遥感数据本质是非线性的，线性映射降维方法无法利用高光谱数据自身的非线性结构。因此，诸多学者提出不同的非线性映射降维方法，主要包括基于核技术的非线性降维方法（如Fauvel M[6]等提出的KPCA、杨国鹏[7]等提出的核Fisher 判别分析）、DONG G J[8]等提出的等距映射（ISOMAP）、罗琴[9]等提出的局部线性嵌入（LLE）等。非线性映射降维方法弥补了线性映射降维方法不能发现高光谱影像数据非线性结构的缺陷，但其处理复杂的非线性特征关系时计算量非常大，大幅增加了计算成本。

现有研究中，没有明确对PCA 算法和KPCA 算法差异性的比较。本文通过设定阈值，计算了主成分分量的个数和降维时间，比较了两种算法的数据压缩能力、计算机运行成本等内部差异性；再加入多层次感知器（MLP）对降维后的数据进行外部差异性分析，基于两种降维算法的分类结果做进一步评价，分析了两种降维算法的优劣。

1 基本原理与实现步骤

1.1 PCA算法

1.1.1 基本原理

PCA 算法是一种基于线性映射的特征提取技术。通过一定变换将高维影像数据变换到一个新的低维空间，使高维数据的最大方差投影在第一个低维空间的坐标（即第一主成分分量）上，第二大方差投影在第二个低维空间的坐标（第二主成分分量）上，以此类推[10]。利用少数几个主成分分量将原始高维影像数据最大限度地保留下来，第一主成分分量包含了原始高维影像数据中的绝大部分信息[11]。PCA 算法主要利用协方差矩阵是一个实对角矩阵的性质，即方差最大化、协方差最小化，来进行降维。

1.1.2 实现步骤

假设高光谱遥感数据有P个波段，数据表示为X=(x1,x2,…,xN)=(X1,X2,…,XP)T，其中Xk为一个N×1 维的列向量（N为高光谱数据的像元数目，即N=m×n，m为行数，n为列数），则X为一个N×P的矩阵，降维后的低维输出维度为d（d≪P）。其主要步骤为[12-14]：

1）计算所有训练样本的均值向量。

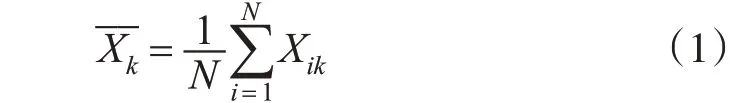
式中，i=1,2,…,N；k=1,2,…,P。

2）计算原始高维数据零均值化的标准矩阵。

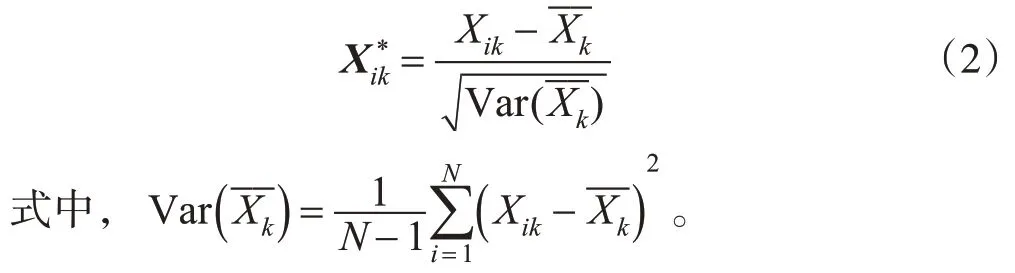
3）计算所有训练样本的协方差矩阵。

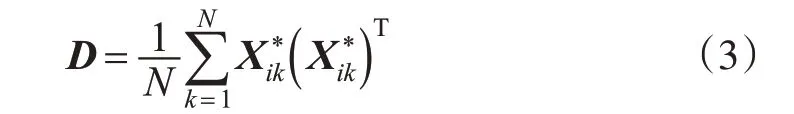
4） 计算协方差矩阵的特征值λ1,λ2,…,λP,λ1≫λ2…≫λP及其对应的特征向量α1,α2,…,αP，并将特征值由大到小进行排序，其特征向量会随特征值的排序依次排列；通过得到的特征值，计算每个主成分所含的贡献率σi和累计贡献率δ。

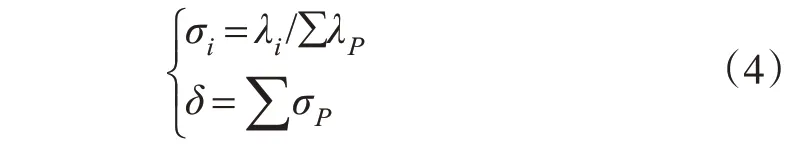
5）取最大的d个特征值（d≪P），将对应的特征向量α1,α2,…,αd组成转换矩阵A=[]α1,α2,…,αd，利用式（5）计算得到原始高光谱遥感影像数据X降至d维的数据Y。

变换后原始影像数据的绝大部分信息排在前面的几个主成分分量中，众多靠后分量包含的信息基本为噪声[15]。因此，PCA 算法在一定程度上起到了降噪的作用。PCA算法的降维流程如图1所示。

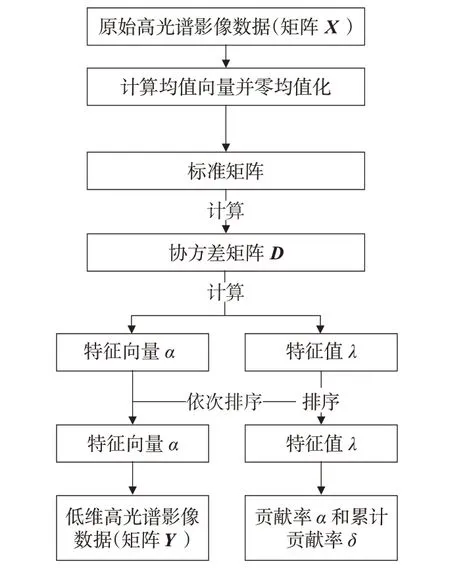
图1 PCA算法降维流程图

1.2 KPCA算法

1.2.1 基本原理

PCA算法一般适用于数据的线性降维，但高光谱数据的本质是非线性的，线性映射降维方法无法表示其非线性结构。为了实现高光谱数据的非线性特征提取，在线性映射降维方法的基础上加入了核函数，将传统线性映射降维方法核化。核化方法采用非线性映射将输入空间的原始数据映射到高维特征空间，在特征空间中进行线性处理，其关键在于引入核函数，忽略具体映射函数的表达式，直接得到低维数据映射到高维后的内积（协方差矩阵的每个元素都是向量的内积）[16]。目前，广泛使用的核函数主要包括[17]：

1）线性核函数：K(x,y)=xTy+c。

2）多项式核函数：K(x,y)=[a(x·y)+c]d，c≥0,d≤N,a为常数。

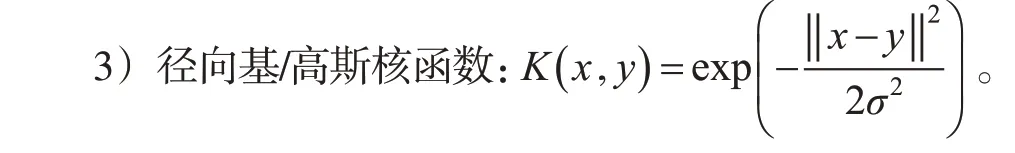
4） 多层感知器核函数（Sigmoid 核函数）：K(x,y)=tanh[s(x·y)+c] ，s、c为常数。

KPCA算法是将输入的矩阵数据X由一个非线性映射Φ 映射到更高维的特征空间ℜ 中，使其线性可分，然后在高维特征空间ℜ 上执行线性PCA，利用核函数求得内积，得到矩阵数据X在特征向量上的投影。其降维基本原理为[16-20]：

假设原始高光谱遥感影像数据矩阵为X=[x1,x2,…,xN]，其中每个样本点Xi为P维列向量，X中共有N个样本。利用一个非线性映射Φ 将矩阵X中的向量Xi映射到高维特征空间ℜ （假设有K维），则有：

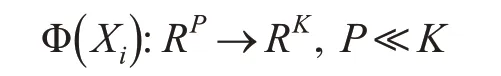
将矩阵X中所有样本都映射到高维特征空间ℜ中，得到一个K×N的新矩阵Φ(X)，即

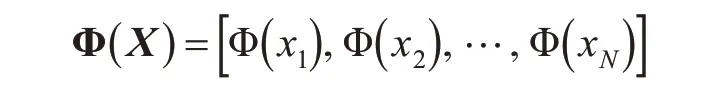
假设矩阵Φ(X)已作中心化处理，则有：

在特征空间ℜ 中，其协方差矩阵为：

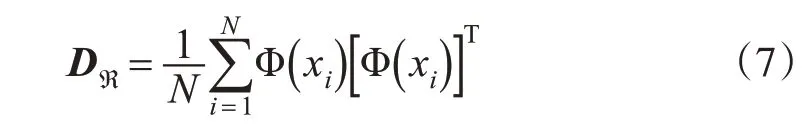
式中，Dℜ为K×K的矩阵。

利用式（8）求解特征空间ℜ 的特征值问题：式中，K维列向量Ρ是特征空间ℜ中对应的特征向量。

将式（7）代入式（8），则有：

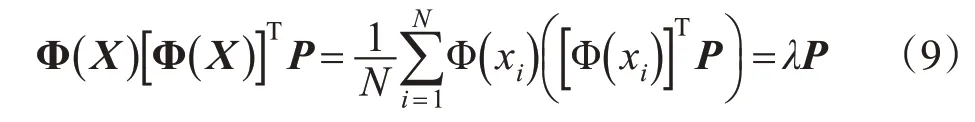
当λ≠0 时，特征向量Ρ的线性表示为：

式中，α为N维列向量[α1,α2,…,αN]T。

此时，求解特征向量的问题随之转化为求解对应α值的问题，将式（10）代入式（9），则有：

Φ(X)[Φ(X)]TΦ(X)α=λΦ(X)α

将两边左乘矩阵[Φ(X)]T，即

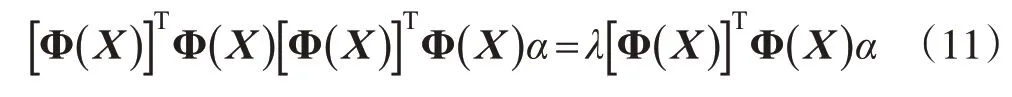
定义一个N×N的矩阵K=[Φ(X)]TΦ(X)，其第i行j列的元素为Ki,j=[Φ(xi)]TΦ(xj)，则式（12）可转化为：

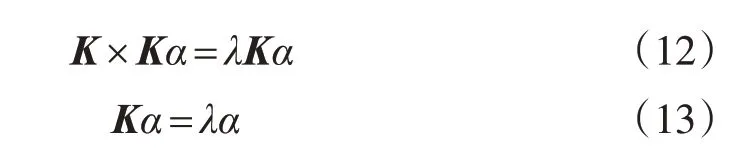
此时得到的特征向量α并不是PCA算法特征值分解时得到的基向量，而是利用特征空间映射样本线性表示时的线性系数。实际上应求得α对应的特征向量P的标准向量，因此需对Ρ进行归一化处理，即

PTP=1

则有：

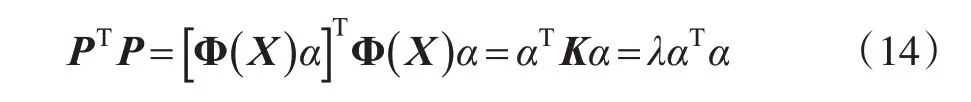
求解得到K的特征值和特征向量α后，再利用式（10）求解得到特征向量Ρ，在KPCA算法特征空间ℜ 中的主成分方向就是Ρ，则原始数据映射到特征空间ℜ 上第j维向量Ρj的投影为：

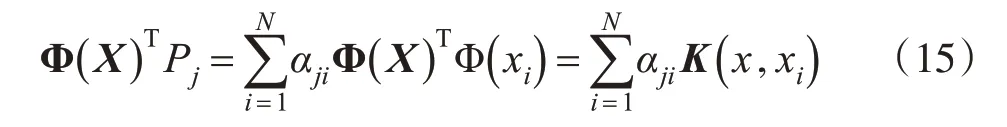
若特征空间ℜ 中的数据未满足中心化条件，则需对矩阵K进行改正，将K͂代替式（13）中的K，即

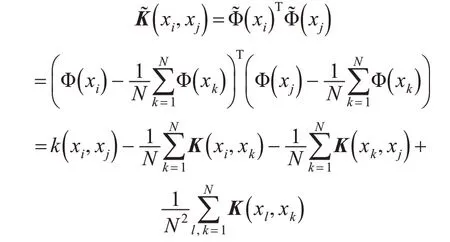
可转化为：

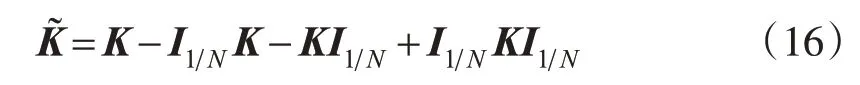
式中，I1N为一个N×N的矩阵（与核矩阵维数相同），其所有元素均为1N。

1.2.2 实现步骤

若高光谱遥感影像数据有M个训练样本，每个样本有P个波段，记X=[X1,X2,…,XM]，将其表示为M×P的矩阵，降维后的低维输出维度为d。其主要步骤为[21]：

1） 将矩阵X映射到特征空间ℜ 中，即Φ(X)=[Φ(x1),Φ(x2),…,Φ(xM)]。

2）选择合适的核函数，对核矩阵作中心化处理，建立标准核矩阵，并计算标准核矩阵，即=K-I1M K-KI1M+I1M KI1M。

3）计算核矩阵K͂的特征值λ1,λ2,…,λP,λ1λ2…≫λP及其对应的特征向量Ρ1,Ρ2,…,ΡP，并将得到的特征值由大到小进行排序，其特征向量会随特征值的排序依次排列。

4） 对特征向量Ρ1,Ρ2,…,ΡP进行正交单位化（Gram-Schmidt 法），得到的特征向量即为核主成分分量α1,α2,…,αP。

5）取最大的d个特征值（d≪P），提取对应的d个主成分分量α1,α2,…,αd，求得投影矩阵Y，即Y=，α=(α1,α2,…,αd)，Y为矩阵X数据经KP⁃CA算法降维后的数据。

KPCA算法降维流程如图2所示。

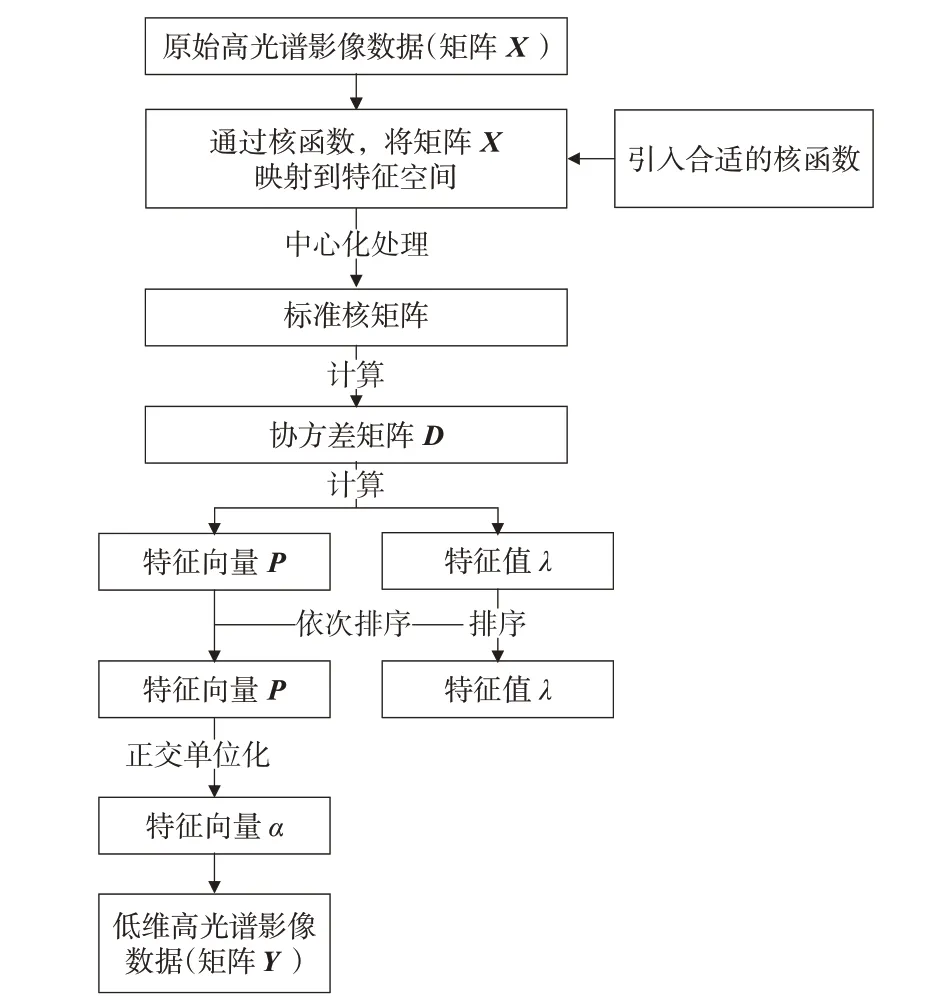
图2 KPCA算法降维流程图

2 实验方法与结果分析

2.1 实验数据

本文选用1992 年AVIRIS 拍摄的Indian Pines（印度松树）数据集。该影像数据集截取145像素×145像素大小作为高光谱遥感影像数据降维的测试数据，共有21 025个像素，其中背景像素10 776个，地物像素10 249个；共有220个波段，但其中20个波段受噪声和水汽影响，因此剔除这20个波段，选用剩余的200个波段作为研究对象。Band43、Band23 和Band10 三个波段叠加形成的假彩色合成图像如图3a所示；印度松树数据集16种地物的真实地物图像如图3b所示。

图3 印度松树测试数据集

2.2 实验结果分析

实验利用Python 编写PCA 和KPCA 两种降维算法，利用印度松树数据集进行测试。为了比较PCA算法与KPCA 算法之间的差异性，设置固定的阈值T（即累积贡献率）≥0.95，得到降维后各主成分分量的贡献率和累计贡献率，重复5 次得其平均值，结果如表1所示。

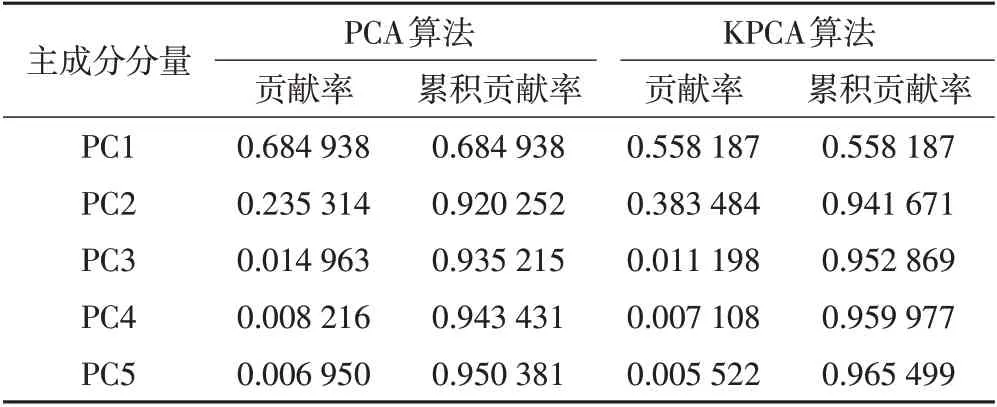
表1 PCA算法和KPCA算法降维后各主成分分量的贡献率与累计贡献率

由表1 可知，原印度松树影像数据200 维包含的信息，经PCA算法降维后其数据前5个主成分分量就表达了整个影像数据95.038 1%的信息，而经KPCA算法降维后其数据仅前3 个主成分分量就包含原始影像数据95.286 9%的信息量，说明PCA算法和KPCA算法均能对高光谱遥感影像数据进行优化处理，达到数据压缩、约简的目的，而KPCA 算法作为PCA 算法的核函数延伸方法，处理高维影像数据时在尽可能包含更多原始信息的基础上具有更强的压缩能力和的更好降维效果。

通过计算两种降维算法的时间，比较了二者的时间复杂度。两种算法均运行5次取平均值，对比其运行成本，PCA算法用时16 s，KPCA算法用时85.6 s，PCA算法的优势较明显。原因在于，KPCA算法做了非线性变换，在高维空间进行协方差矩阵的特征值分解，再采用与PCA 算法相同的方式进行降维，在高维空间中KP⁃CA算法运用了核函数运算，计算量远超于PCA算法。

为进一步对比两种降维算法的差异性，充分分析二者的特征差异性，本文选择基于分类应用的降维效果评估方法，以MLP为分类器进行分类。MLP分类器是目前遥感领域的主流分类器之一，由许多相同的处理单元并联组合而成，能进行大量简单单元的并行活动，对信息的处理能力、普适性较强，较适合高光谱遥感数据这类大型数据的分类处理，在遥感影像分类中有较多的应用实例，更容易验证PCA 算法和KPCA算法的降维效果。

两种降维算法基于MLP分类应用的降维效果如图4所示，可以看出，第1、7和8种地物的分类准确率为100%，由于这3 种地物样本太少，无法做到有效预测，因此其分类没有价值。地物序号为0 的是影像的背景值，是分类中错分的主要因素。总体而言，KP⁃CA算法经分类后各地物的分类精度略优于PCA算法。

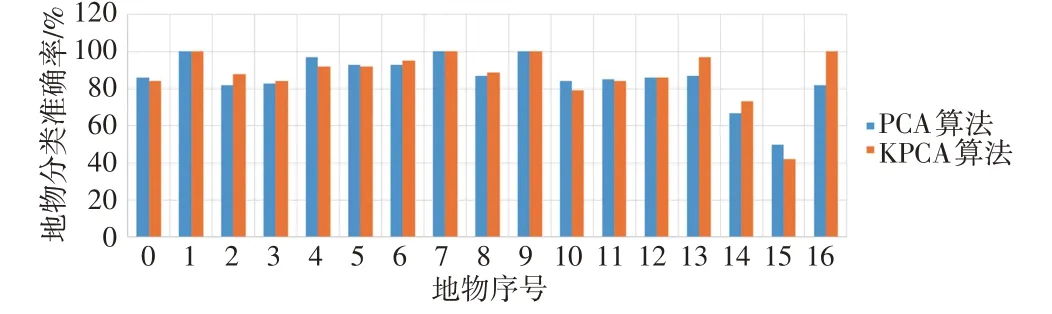
图4 基于MLP分类应用的降维效果对比

由两种降维算法分别经MLP分类器分类后的结果可知，KPCA 算法的总体精度高于PCA 算法，错误分类比例也较少，但分类的时间略长，如表2所示。

表2 基于两种降维数据的MLP分类结果精度统计表

3 结 语

1）PCA算法和KPCA算法通过舍去一部分原始影像中不必要的数据信息来降低维度，使得样本采样更密集，缓解了维度灾难，降低了噪声影响。实验结果表明，在相同数量的主成分分量条件下，KPCA 算法能更很好地包含高光谱遥感影像中的原始信息，具有比PCA算法更好的信息集中性。

2）KPCA算法在低维空间应用核函数，巧妙地从低维升至高维，在高维空间中实现非线性映射，但大幅增加了算法的复杂度，降低了高光谱遥感影像数据降维处理的时效性。在这一点上，PCA算法计算量小且速度快，具有更大的优势。

3）KPCA算法提取的各分量特征在后续的影像分类中具有良好的表现，各地物总体精度均高于PCA算法，具有足够的适用性。

4）PCA 算法在提取遥感数据主要信息的同时将所有样本当作一个整体看待，寻找均方误差最小的线性映射投影，却忽略了地物的类别属性，导致后续的分类精度降低，出现比KPCA算法更多的错分和漏分现象。

由于高光谱数据特征维度过高，对后续的研究易造成巨大影响，因此找到一个既能充分利用高光谱丰富数据量又能降低消耗成本的降维方法才能解决处理高光谱数据成本大的问题。同时，选择不同的核函数也会不同程度地影响降维与分类的效果。因此，非线性KPCA算法的参数选择也是一个降维算法的改进方向。