建筑沉降监测与组合预测模型研究

梁 珂，李文阳，王宏宇，刘伟东，任秀波

（1. 自然资源部第一大地测量队，陕西 西安 710000；2. 长安大学地质工程与测绘学院，陕西 西安 710054）

众所周知，在施工和运营期间，建筑物受到地质、气候以及建筑物自身原因或邻近地下工程建设的影响，基础部分受力不均匀，将出现不同程度的沉降[1]。建筑物沉降往往受各方面的影响，沉降情况大不相同[2]。在各种因素的影响下，建筑物的沉降量在短时间或某段时间内会发生巨大变化，导致建筑基础部分或建筑物结构发生不可逆的变化，极大影响建筑物的正常使用，甚至对人民生命财产造成巨大损失[3]。建筑物沉降监测的目的在于收集、分析、总结获取的变形数据，得出其变化规律，从而科学准确地预测建筑物未来的变形趋势，快速做出补救措施。此外，需根据建筑场地的环境，制定一套合理的、详尽的监测方案[4-5]。

因此，需要预测模型对建筑沉降进行准确、科学的预测，进而及时发现问题并解决。通常来讲，单一预测模型无法综合各种有效信息对变形体进行准确预测，将导致部分信息的遗漏，预测精度不高[6-7]。为提高预测精度，保证建筑物的安全运营，需要结合各种变形因素，将各单一模型进行最优组合。我国对组合预测模型的研究相对较晚，但逐渐也有十几年的研究历史。我国研究学者针对组合模型撰写过许多文章，发表在各大期刊，反响很好[8-10]。随着研究的不断深入，我国研究学者在组合模型的众多难点中有了重要创新与突破，包括组合预测、自适应预测和马尔科夫预测等[11-13]。如何准确监测建筑物的沉降[14]，并对其未来的变形趋势做出科学预测是本文的研究重点[15]。本文研究的主要内容为：

1）介绍建筑沉降监测的相关概念，获取沉降监测数据、精度选择、数据处理方法。

2）介绍组合预测模型的原理与分类，单一模型中的灰色系统模型和时间序列模型以及一些常见的非线性函数模型。

3）分别利用非线性函数中的S型函数、二次曲线函数、灰色模型对工程实例进行分析预报。

4）将灰色模型分别与S型函数、二次曲线函数进行组合，再通过Matlab软件编程实现对工程实例的分析预报，并将各模型处理结果进行比较，得出结论。

1 组合预测模型研究

在实际工程中，建筑沉降预测结果会受多方面因素的影响，为减少该影响，可选择多个单一预测模型进行预测。由于不同预测模型的理论支撑不同，其预测结果也往往不同。因此，为提高预测精度，将各单一预测模型进行最优组合是一种很全面的预测方法。组合预测模型能综合各单一模型提供的有效信息，更加系统、全面地对系统进行预测，且能有效减少随机因素的影响。如何赋予各单一模型预测结果的权重是提高预测精度、减少有效信息遗漏的关键。

1.1 时间序列模型

时间序列是指将观测数据按时间或空间顺序进行排列[16]。时间序列分析方法的理论支撑是信息处理技术和现代统计学，用以研究信息在某种趋势的随机变化过程中的规律。时间序列模型研究的只是因自变量自身变化的规律，和其他变量无关。

1.2 灰色系统理论

灰色系统理论是指信息不充分且原始数据较少的不确定性系统通过处理已知信息，提取其中有用的信息，对系统运行进行准确描述[17-18]。GM(m,n)模型是有且只有一个单一变量的一阶微分方程模型，只要一个数列即可建模。若检验后发现模型的精度不够，则需建立合适的残差模型来补偿精度。灰色模型常用的补偿精度方法是后验差检验。

2 工程实例分析

2.1 工程概况

宿迁中学新校区位于江苏省宿迁市宿城区，南边为微山湖路，西边为红海路，东边为南海路。综合楼为框架结构，主楼6 层，局部1～2 层，建筑面积约为2 万m2。观测数据时间为2007-02-16—2007-08-20，历时6 个月。本文只选取其中一组数据（18 号点），共19期数据，沉降折线如图1所示。本文采用组合模型进行预测模型分析。

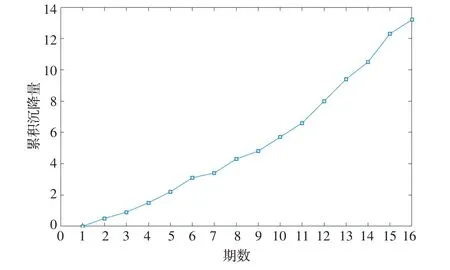
图1 沉降折线图

2.2 S型函数

2.2.1 S型函数建模

S型函数的表达式为：

S型函数建模成果如图2所示。

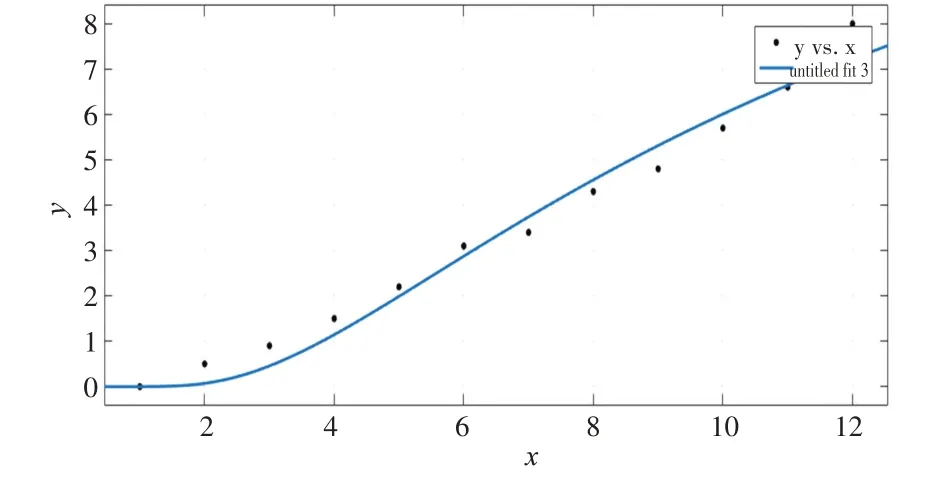
图2 S型函数建模成果

2.2.2 数据处理

S型函数模型沉降拟合结果如表1所示，S型函数模型沉降拟合对比图如图3 所示。根据上述结果，本文利用S型函数对13～16期的沉降数据进行预测，结果如表2所示。S型函数模型沉降预测对比图如图4所示。

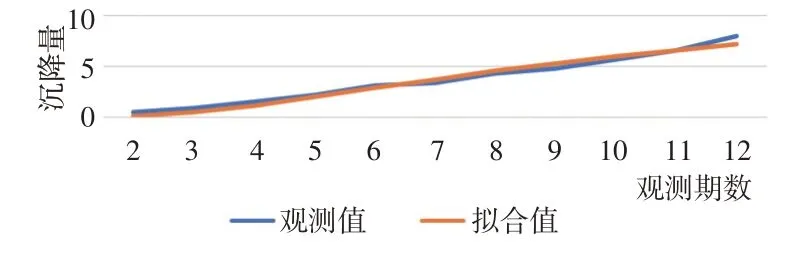
图3 S型函数模型沉降拟合对比图/mm

图4 S型函数模型沉降预测对比图/mm

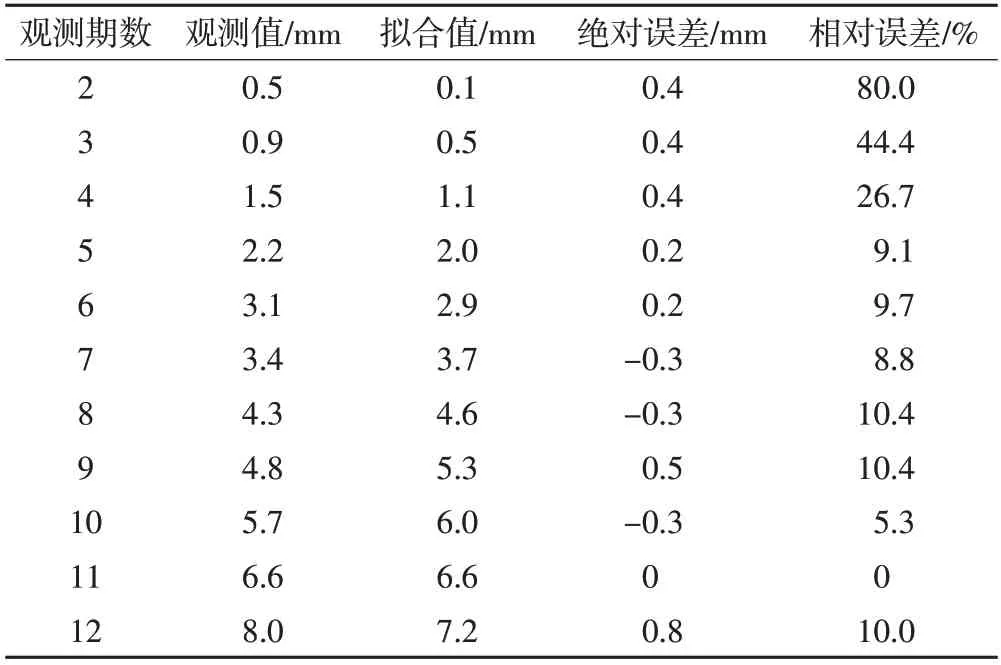
表1 S型函数模型沉降拟合检测表

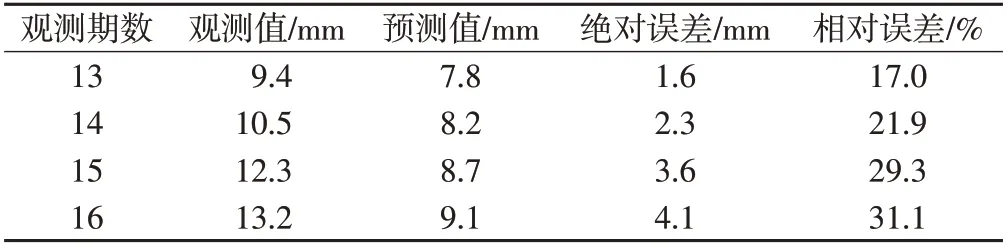
表2 S型函数沉降预测检测表

2.2.3 成果评价

18 号点的沉降量点位基本都在S 型函数图像的两侧，且与图像的趋势相距不远，前12期拟合值与观测值的误差很小，但预测值与观测值的误差越来越大，由此可以判定，随着观测期数的增加，S 型函数模型的预测精度将大大下降。

2.3 二次曲线函数

2.3.1 二次曲线函数建模

二次曲线函数的表达式为：

二次曲线函数建模成果如图5所示。

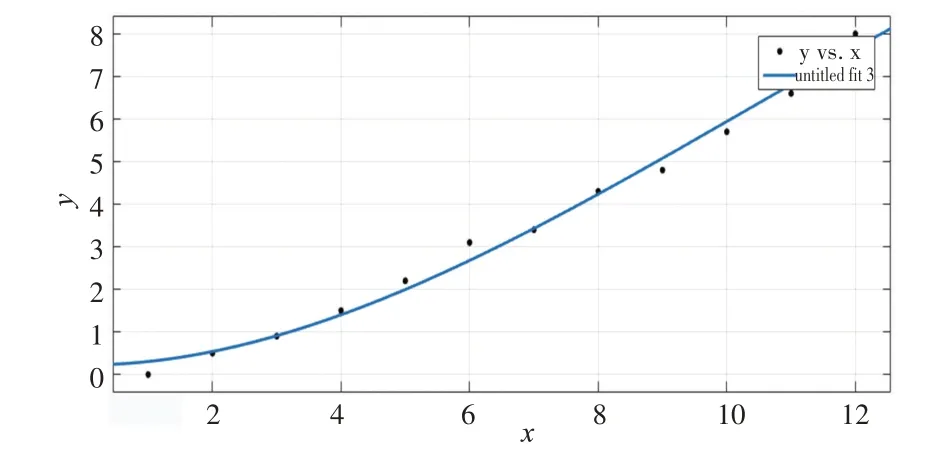
图5 二次曲线函数建模成果

2.3.2 数据处理

二次曲线函数模型沉降拟合结果如表3 所示，二次曲线函数模型沉降拟合对比图如图6 所示。根据上述结果，本文利用二次曲线函数对13～16 期的沉降数据进行预测，结果如表4 所示。二次曲线函数模型沉降预测对比图如图7所示。

表3 二次曲线函数模型沉降拟合检验表

图6 二次曲线函数模型沉降拟合对比图/mm

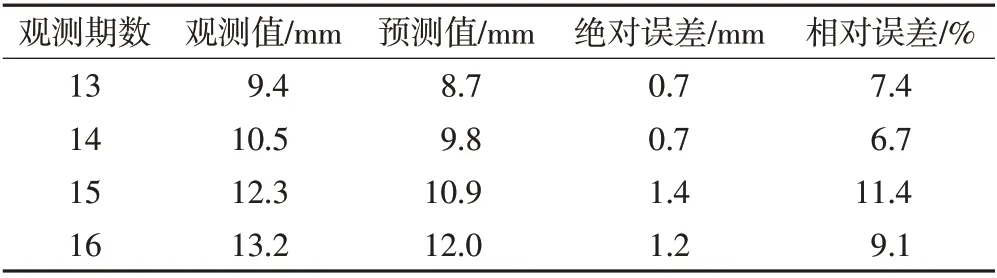
表4 二次曲线函数沉降预测检测表

图7 二次曲线函数模型沉降预测对比图/mm

2.3.3 成果评价

沉降量的点位具有一定规则性地分布在二次曲线函数的两侧，且离散程度不大。拟合的平均误差较小，对13～16 期的沉降量进行预测，所得预测值与观测值的平均误差为8.7%，预测精度相对较好。

2.4 灰色模型

2.4.1 GM（1，1）建模

GM（1，1）模型一般要求参与预测的原始数据不少于4 个，这样才能得到较好的预测效果。本文研究了灰色模型步长与预测效果之间的关系，通过对比不同步长的预测结果发现，步长太长反而会影响预测精度，因此选择7～12期的观测数据作为原始数据建立灰色模型，进而预测13～16 期的沉降值。灰色模型图像如图8所示。

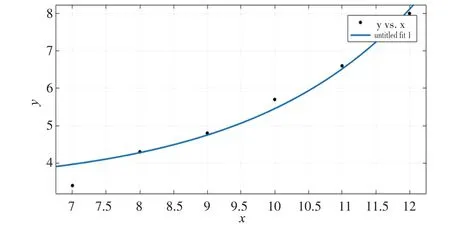
图8 灰色模型图像

2.4.2 数据处理

GM（1，1）模型沉降拟合结果如表5所示，GM（1，1）模型沉降拟合对比图如图9 所示。根据上述结果，本文利用GM（1，1）模型对13～16 期的沉降数据进行预测，结果如表6 所示。GM（1，1）模型沉降预测对比图如图10所示。

表5 GM（1，1）模型沉降拟合检测表

图9 GM（1，1）模型沉降拟合对比图/mm

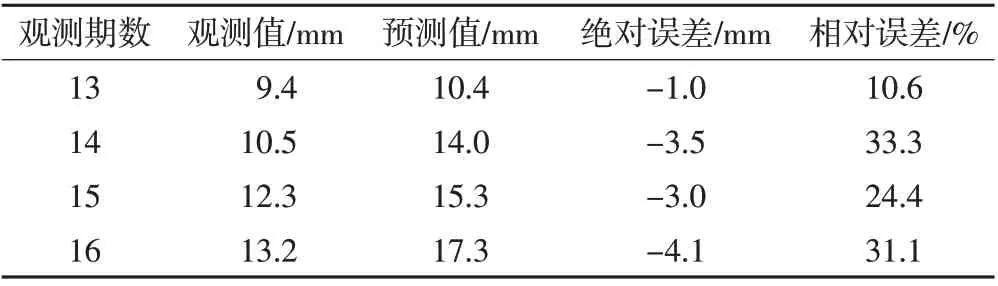
表6 GM（1，1）模型沉降预测检测表

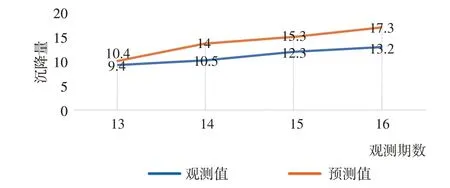
图10 GM（1，1）模型沉降预测对比图/mm

2.4.3 成果评价

根据拟合结果来看，GM（1，1）模型对18 号点的预测较为理想，预测点位趋势基本符合实测变形趋势；但从18 号点13～16 期沉降量预测结果来看，结果并不理想，因此灰色模型在步长的选择上很关键，步长过长将影响预测精度。通过计算对比发现，在本工程中灰色模型适合短期的预测，后期精度将逐渐下降。

2.5 组合预测模型

2.5.1 灰色模型与S型函数的组合模型

通过Matlab 计算得到该组合模型的预测方程为：

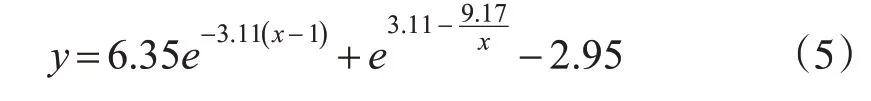
灰色模型与S 型函数的组合模型图像如图11 所示。本文利用该组合模型对18 号点7～12 期沉降量进行拟合，结果如表7 所示。灰色模型与S 型函数组合模型沉降拟合对比图如图12所示。根据上述结果，本文利用灰色模型与S型函数组合模型对18号点13～16期沉降量进行预测，结果如表8 所示。灰色模型与S 型函数组合模型沉降预测对比图如图13所示。

图11 灰色模型与S型函数组合模型图像

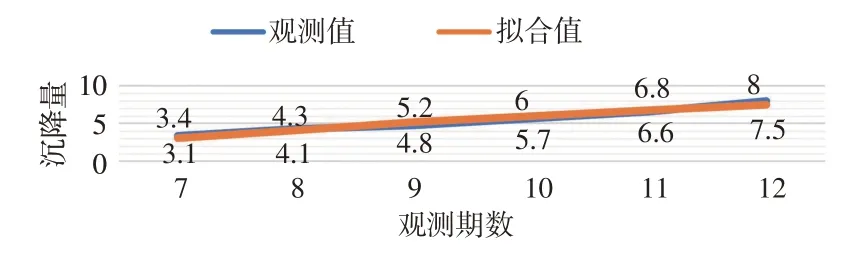
图12 灰色模型与S型函数组合模型沉降拟合对比图/mm

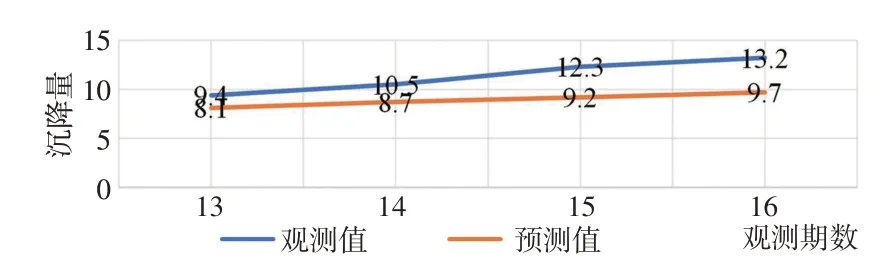
图13 灰色模型与S型函数组合模型沉降预测对比图/mm

表7 灰色模型与S型函数组合模型沉降拟合检测表

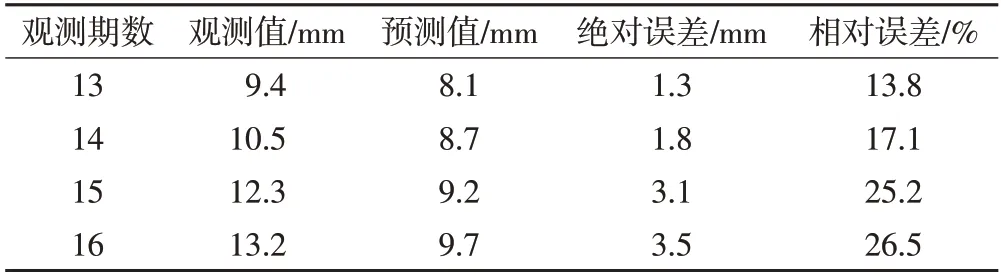
表8 灰色模型与S型函数组合模型沉降预测检测表

2.5.2 灰色模型与二次曲线函数的组合模型

利用Matlab计算得到该组合模型的预测方程为：

灰色模型与二次曲线函数组合模型图像如图14所示。本文利用该组合模型对18 号点7～12 期沉降量进行拟合，结果如表9 所示。灰色模型与二次曲线函数组合模型沉降拟合对比图如图15 所示。根据上述结果，本文利用灰色模型与二次曲线函数组合模型对18号点13～16期沉降量进行预测，结果如表10所示。灰色模型与二次曲线函数组合模型沉降预测对比图如图16所示。

图14 灰色模型与二次曲线函数组合模型图像

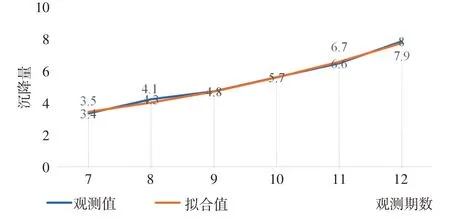
图15 灰色模型与二次曲线函数组合模型沉降拟合对比图/mm

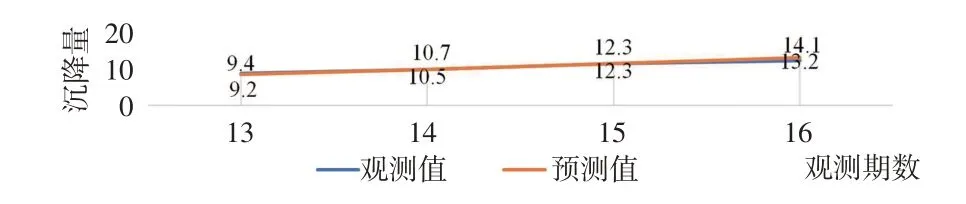
图16 灰色模型与二次曲线函数组合模型沉降预测对比图/mm

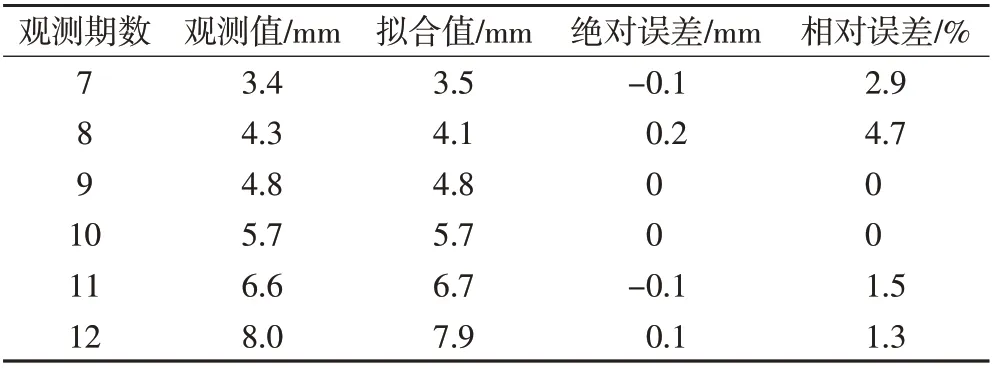
表9 灰色模型与二次曲线函数组合模型沉降拟合检测表

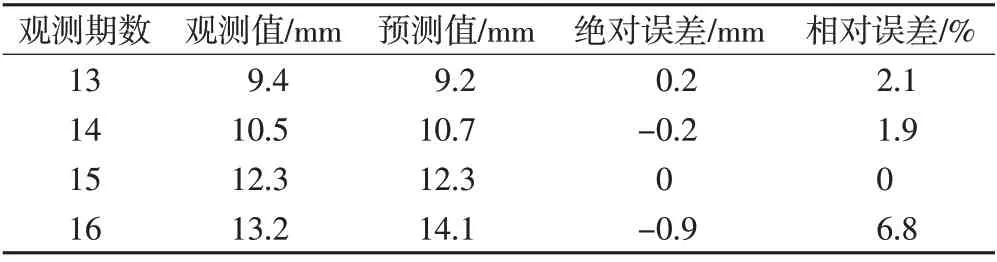
表10 灰色模型与二次曲线函数组合模型沉降预测检测表

2.6 各种预测模型预测结果精度分析

本文分别利用S 型函数、二次曲线函数、灰色模型、灰色模型与S 型函数的组合模型、灰色模型与二次曲线函数的组合模型对18号点13～16期的沉降量进行预测，得到了不同的预测效果。各模型的精度如表11 所示，可以看出，灰色二次曲线函数组合模型的外符合精度最高。

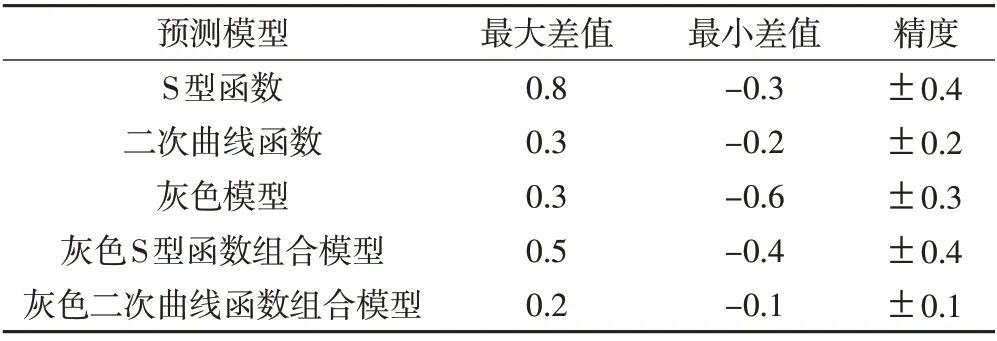
表11 各模型精度结果/mm

各模型预测值与实测值的对比如图17所示，可以看出，无论是单一模型还是组合模型，它们都有其预测适用的特定范围，5 种预测模型的预测精度均不相同，这与模型本身以及已知的原始数据有关。综合来看，5 种预测模型中灰色二次曲线函数组合模型的预测效果最好。组合模型的预测精度普遍高于单一模型，其原因是在建模时单一模型不能考虑所有情况，而组合模型则可综合考虑多方面问题，思路相对周全。组合模型能较好地对建筑沉降进行准确预测，但若存在突变数据的影响，组合模型的预测精度就未必比单一模型高，如18号点灰色模型的平均误差比灰色二次曲线组合模型略优，由此可以判定，变形预测精度不光取决于预测模型本身，还与原始观测数据的质量密切相关。

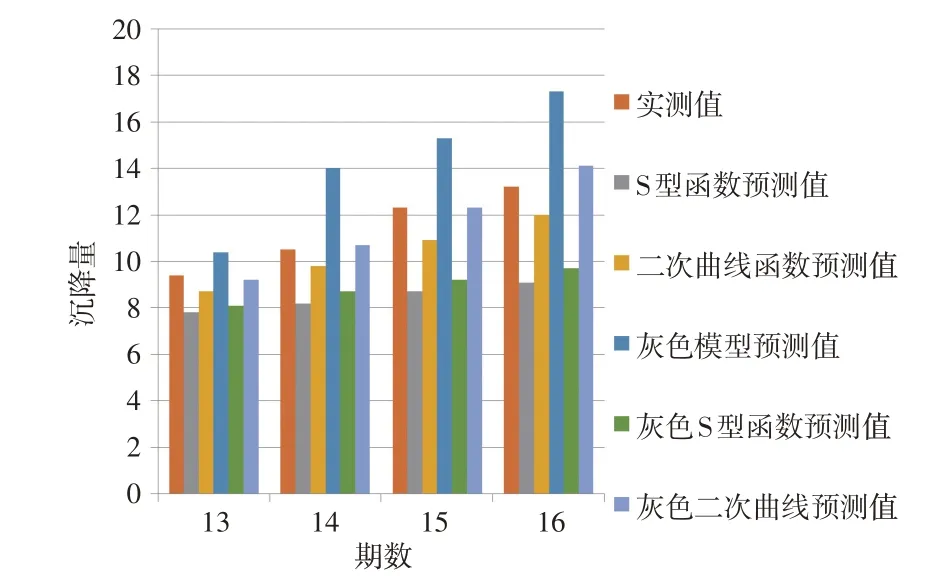
图17 各模型预测值与实测值的对比图/mm

3 结 语

我国经济实力的飞速发展，工程建设的快速推进以及复杂的建筑工程不断出现都对建筑沉降监测提出了更高的要求。为了保证人民生命财产安全，建筑沉降监测意义重大。本文结合宿迁中学新校区的沉降监测项目，首先讨论了建筑沉降监测的概念和方法，制定了监测方案，并对各种预测模型进行了理论研究；然后对S 型函数、二次曲线函数、灰色模型、灰色S 型函数组合模型、灰色二次曲线函数组合模型进行了工程分析，对比了5 种预测模型的预测效果。

1）本文总结了建筑沉降监测的意义和目的，讨论了监测方法，制定了监测方案。在监测网布设时选择稳定的点作为基准点和监测点，采用专用的测量仪器，运用科学的测量方法，保证观测数据的准确性和可靠性，可为后期的沉降预测提供很好的辅助作用。

2）本文研究了组合模型建模的常见方法，并分别对S 型函数、二次曲线函数、灰色模型进行建模。

3）本文分别将灰色模型与S型函数、二次曲线函数进行组合，采用相同的方法进行数据处理，并对比分析了各预测模型的预测效果和精度，最后得出一个准确预测的模型。