临近空间飞行器超螺旋滑模自适应姿态控制

周奕雯， 仲科伟， 张万超， 金一欢， 蒋虎超

上海航天控制技术研究所, 上海 201109

0 引 言

临近空间飞行器因其飞行速度快、突防能力强等优点成为世界各国争相研究的热点.临近空间飞行器在快速机动过程中，因大攻角与快速滚转的需求同时出现，将造成三通道之间产生强烈的耦合，在侧向通道形成较大的侧滑角.由于所在的环境复杂多变，气动参数摄动严重，这些因素决定了临近空间飞行器是一个存在严重不确定性的非线性系统.因此，临近空间飞行器在快速机动过程中，处于强耦合、强非线性、强不确定的飞行状态下，需要重点考虑控制系统的指令跟踪以及抗干扰能力.

针对上述难题，文献[1]将动态逆与鲁棒控制方法相结合，采用鲁棒控制策略补偿系统参数不确定性和外界干扰，但存在逆误差.文献[2]在假设外界干扰变化缓慢的前提下，提出了一种自适应反步控制律.滑模变结构控制方法具有快速响应、对扰动不敏感和设计简单等优点[3]，因此常应用于临近空间飞行器控制系统设计.文献[4]在反步设计的每一步中均采用滑模控制设计虚拟控制量来补偿不确定性的影响，但该方法要求每个子系统的不确定项信息已知.文献[5]针对执行器的多故障问题，设计了一种快速自适应终端容错控制器，但存在抖振现象.为抑制抖振，并保证鲁棒性，文献[6]采用饱和函数代替符号函数，然而饱和函数法会使得系统轨迹稳定在滑模面附近而非滑模面上，降低了控制精度.通过高阶滑模来抑制抖振可以提高控制精度并且增强系统对干扰的鲁棒性.文献[7]提出了一种基于扩张观测器的自适应高阶滑模控制方案，通过观测器在线重构系统中的干扰.文献[8]提出了一种快速超螺旋算法，通过在普通超螺旋算法中加入线性项，提高了算法的收敛速度，并基于此算法设计干扰观测器对干扰连续估计和补偿.文献[9]在干扰上界未知的前提下，设计了一种自适应律，提出一种自适应超螺旋算法，应用于吸气式高超声速飞行器控制，成功削弱了抖振.上述算法由于积分项中含有不连续的符号函数，只能得到连续的控制输入，但不光滑，还存在参数过大估计的问题.

针对具有强非线性、强耦合、强不确定性的临近空间飞行器BTT控制模型，提出了一种改进的超螺旋滑模自适应控制方法，精确跟踪快速滚转机动时的姿态指令，设计自适应控制律来选取控制参数，提高响应速度和鲁棒性能，抑制滑模控制存在的抖振现象.

1 建立飞行器数学模型

将临近空间飞行器动力学方程进行合理简化，建立六自由度刚体数学模型[10]：忽略重力影响；飞行器满足面对称条件，即惯性积Jxz=Jyz=0，Jxy数值较小可忽略；认为飞行器巡航阶段速度变化缓慢，即飞行速度近似为常数；认为sinα≈α，cosα≈1，sinβ≈β，cosβ≈1，tanα≈α，并忽略含有攻角、侧滑角的二阶小量，即认为α2≈β2≈αβ≈0。

以飞行器的滚转角γ、侧滑角β和攻角α3个角度以及弹体坐标系中的滚转角速度ωx、偏航角速度ωy和俯仰角速度ωz3个转动角速度为状态变量，以副翼偏转角δx、方向舵面偏转角δy和升降舵面偏转角δz为控制量，建立临近空间飞行器非线性耦合数学模型：

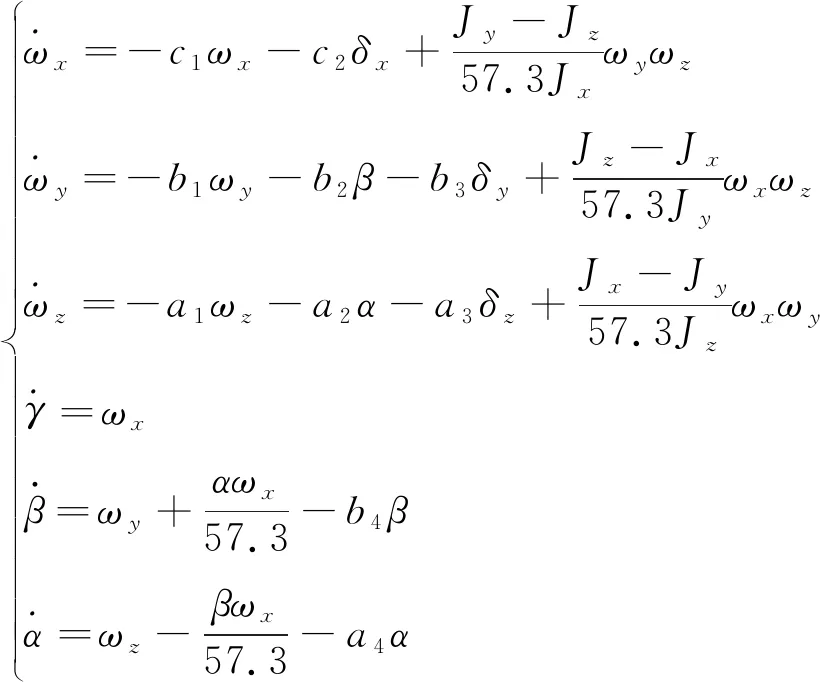
(1)

其中，ai,bi,ci分别为俯仰通道、偏航通道和滚转通道相应的动力系数，具体定义见参考文献[10]。

用一阶惯性系统来等效实际舵机，控制目标是跟踪攻角指令αc和滚转角指令γc并将侧滑角指令βc置零，以实现临近空间飞行器倾斜转弯控制。

令系统输出Y=[γβα]T，系统状态量X=[γβαωxωyωz]T，控制输入U=[δxδyδz]T，分别对输出变量Y求二阶导数可以得到与控制输入相关的表达式：

(2)

式中

考虑如下含不确定项的二阶被控对象：

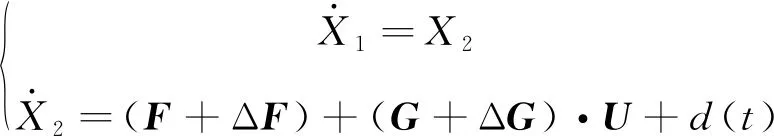
(3)

其中，为外加干扰，ΔF和ΔG为系统不确定性部分.

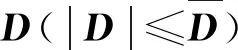
2 控制器设计与稳定性分析

滑模控制的不变性可有效抵抗干扰，但由于未建模动态和非理想的切换特性，传统滑模存在抖振现象，这种抖动会引起舵面的剧烈振荡，大量消耗系统的能量.超螺旋算法通过积分获得实际的控制变量，因此不含高频切换量，从而可以削弱抖振，具有强鲁棒性和高精度的控制性能.

超螺旋算法的形式如下：

(4)

参考文献[11]中控制参数λ和α的选取需要已知干扰导数的上界，这在实际应用中难以获取。

传统超螺旋算法有以下不足[12]：

1)当系统距平衡点较远时，收敛速度慢；

2)积分项含有符号函数，控制指令是不光滑的，会影响控制性能；

3)控制参数的选取需要已知干扰的边界信息.

针对上述问题，对超螺旋滑模算法进行改进：

1)在控制指令中加入线性项ks1以加快收敛速度；

2)将积分项下符号函数sign(s1)改为双曲正切函数tanh(s1)，保证控制量的光滑性；

3)在干扰导数上界信息未知的情况下，设计一种自适应律来自动调整控制参数，同时避免参数过大，造成系统不稳定.

2.1 超螺旋滑模控制器设计

下面简化为一维变量并省略t表示.假设目标指令为xd，跟踪误差为e=x1-xd.控制器设计步骤如下[13]：

因此，设计控制器：

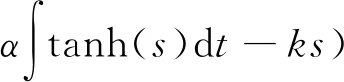
其中，参数ω1,γ1,u,sM,ε,β均为正的实数.

2.2 稳定性分析

为方便证明，下面以符号函数sign(s)代替双曲正切函数tanh(s).

定义Lyapunov函数

则

定义Lyapunov函数[14]

则

可得

由于

为保证Q正定，令

2.3 自适应律设计

在设计步骤中增加包含参数误差的二次项Lyapunov函数，从而引入参数调整律的求取步骤，通过在线修正控制参数保证闭环系统的动态品质.

定义Lyapunov函数[15]

其中，参数γ1,γ2为正的实数.

则

η=min(r,ω1,ω2)

因此

为了保证有限时间收敛，令ξ=0，同时避免增益过大，故控制参数λ和α的自适应律为

通过自适应律调整控制增益，对未知不确定性上界的系统仍能有较好的控制效果.在自适应律中引入tanh(|s|-u)，保证切换增益的有界性，避免参数过分估计造成系统不稳的问题.由Lyapunov稳定性理论可知，该控制系统在参数不确定以及干扰的情况下具有稳定性和自适应性.

3 仿真结果

传统超螺旋滑模控制与改进的超螺旋滑模控制效果对比如图1所示.仿真结果显示改进的超螺旋滑模方法能够提高响应速度和控制精度，控制效果更光滑.

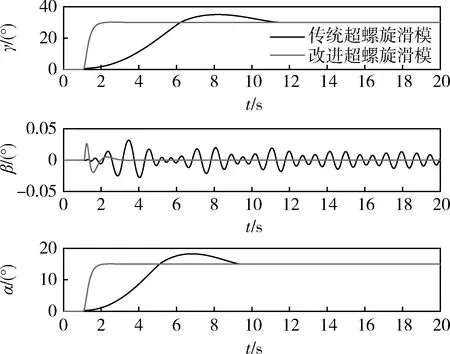
图1 改进的超螺旋滑模控制效果图

对临近空间飞行器三通道耦合非线性模型进行定点仿真，验证改进的超螺旋滑模自适应控制器的指令跟踪能力和鲁棒性.选取典型巡航阶段：飞行高度23 km，速度5Ma的飞行特征点状态数据进行仿真.对于滚转通道，飞行器需要通过快速滚转以满足机动的需求，因此其滚转角的跳变应比较明显，滚转角速度较大；对于偏航通道，倾斜转弯的控制模式要求其侧滑角应保持在±3°以内；俯仰通道，保持固定攻角，维持进气道正常工作.根据以上分析设定下面仿真条件，来检验系统在不同条件下的适应能力.控制参数的选取如表1所示.

表1 控制器参数

3.1 方波指令跟踪仿真结果

攻角αc为15°的阶跃指令，始终保持侧滑角βc为0°，滚转角γc为幅值45°的交叉方波指令，这对滚转控制性能要求很高，在保持攻角和侧滑角不变的情况下进行大范围的滚转机动，将线性滑模控制法(黑色实线)与改进的超螺旋自适应控制法(蓝色实线)对比，仿真结果如图2和图3所示，控制参数λ和α自适应变化情况如图4所示.

图2 滚转角、侧滑角和攻角跟踪曲线

图3 舵响应曲线

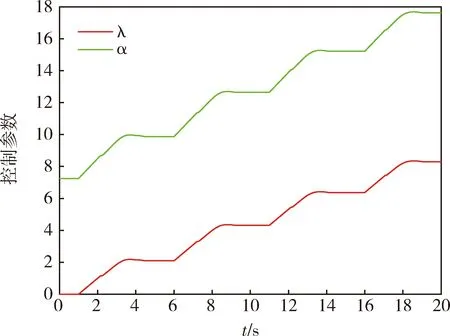
图4 自适应曲线

从仿真结果来看，线性滑模控制方法侧滑角最大偏差为0.8°且存在剧烈抖振.改进的超螺旋自适应控制方法跟踪攻角指令上升时间为0.73 s，跟踪滚转指令上升时间为0.69 s，攻角和侧滑角在滚转机动时出现偏差，攻角偏差小于4°并在1.2 s内消除偏差，侧滑角偏差小于0.25°随后在0.8 s内消除偏差，控制量光滑.仿真结果表明在快速滚转机动过程中改进的超螺旋自适应控制方法能够实现姿态指令的精确跟踪并且能够削弱抖振，控制参数具有自适应能力.

3.2 抗干扰仿真结果

下面验证控制器在强不确定性下的抗干扰能力，同时考虑了外界干扰和气动参数摄动.攻角αc为15°的阶跃指令，保持侧滑角βc为0°，滚转角γc为30°的阶跃指令，滚转通道分别加入3种干扰：5～10 s时加入3°的副翼等效舵偏干扰；15～20 s时加入正弦干扰D_ωx=100sin(2πt)；25～30 s时加入[-100,100]均匀分布的高斯白噪声干扰.考虑气动建模误差，将气动参数进行±30%拉偏.综合考虑控制器在外界干扰和气动拉偏条件下的控制性能，仿真结果如图5和图6所示.

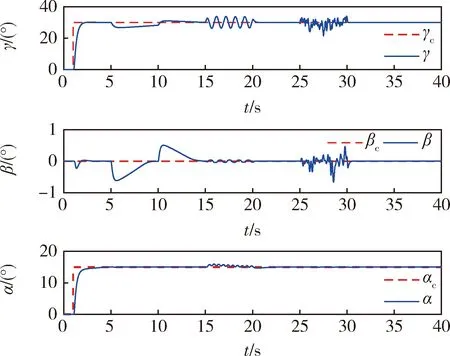
图5 +30%气动参数拉偏干扰仿真结果

图6 -30%气动参数拉偏干扰仿真结果

在加入外界干扰和气动参数拉偏±30%的情况下，滚动角和攻角能精确控制，不影响系统的快速性和稳定性.侧滑角保持在±1°以内，可以满足临近空间飞行器倾斜转弯协调控制的要求.仿真结果证实了改进的超螺旋自适应控制方法具有较强的鲁棒性能.

4 结 论

针对临近空间飞行器快速滚转机动过程中的姿态控制问题，设计并改进了超螺旋滑模自适应控制器，利用类二次型Lyapunov函数给出了闭环系统的稳定性证明.该方法在传统超螺旋滑模算法的基础上，增加了线性项并将积分项下改为连续函数，在复合干扰变化率有界但界限未知情况下，设计了超螺旋滑模控制参数的自适应律，同时避免参数过分估计，造成系统不稳定.控制系统能够精确跟踪指令信号，具有良好的鲁棒性能并且削弱抖振，避免剧烈抖振对舵机造成损坏，具有工程应用价值.本文假设系统模型的结构已知，后续将对系统模型未知的情况进一步开展研究.