轻质高刚仿生杆及其在柔性机构中的仿真分析

张述卿，叶 壮，郜军霞，邵 超，李 根

1. 北京控制工程研究所,北京 100094

2. 北京轩宇空间科技有限公司，北京 100190

0 引言

在空间机构领域，轻质高刚结构可有效减少结构的质量，降低发射成本，提高产品机械性能.结构解剖表明水生植物香蒲的杆径细长且可达数米，杆部几乎皆为多腔体中空结构，杆部截面形状约为半圆形，基于这种轻质高刚结构特点的仿生杆结构具有广泛的空间应用前景，例如可用于以杆件为基本受力单元的天线展开机构、磁力矩器长臂杆、空间站超长操作臂杆等空间大型机构，还可用于精密定位、精密测量等空间柔性机构.

电磁力平衡传感器作为一种高精密测力传感器，分辨率普遍可达被测最大载荷的十万分之一，其将在空间操控、行星探测等领域发挥重要作用.例如在行星探测中通过电磁力平衡传感器对已知质量量块的测量，可以标定行星表面引力的大小.如果将轻质仿生杆应用到传感器的精密机构设计中，可减轻传感器结构质量，为空间探测节约发射和运输成本.

柔性铰链作为柔性单元由一块材料切削而成，利用材料的弹性变形在相邻刚性杆之间产生相对运动，消除了装配间隙引起的位移误差，运动精度高[1-3]，已被广泛用于高精密电磁力平衡传感器[4]，在该领域目前国外技术处于领先地位，如德国赛多利斯sartorius、瑞士梅特勒托利多Mettler-Toledo、美国奥豪斯(Ohaus)等公司[5,6].

本文通过对电磁力平衡传感器中柔性机构的理论分析揭示了其误差来源，采用轻质高刚仿生杆结构作为刚性承力结构，并采用实心材料的柔性转动单元构建了一种精密柔性机构，通过有限元仿真分析探索仿生轻质高刚杆的应用效果，为仿生杆在空间精密机构领域的应用提供参考.

1 轻质高刚仿生杆结构

1.1 香蒲杆结构解剖及力学测试

从总高度不小于200 mm的香蒲杆长度中点部位取样本，如图1所示香蒲杆结构组成可分为平形外壁、弧形外壁、横向膜、纵向膜四部分.

图1 香蒲杆解剖结构

通过对样本测量，平形和弧形外壁厚度约为0.4～0.8 mm，横向和纵向膜厚度约为0.1～0.3 mm，纵向膜间隔约为1～2 mm，横向膜间隔约为纵向膜间隔的2～3倍.

如图2所示，取悬臂长度为50 mm的香蒲杆，一端固定约束，另一端分别从平形外壁、弧形外壁和侧向3个方向施加正压力，各向力位移曲线、刚度位移曲线分别如图3、图4和图5所示.

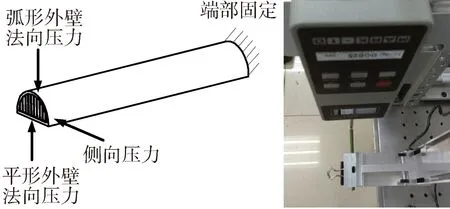
图2 香蒲杆力学测试示意图

图3 平形外壁力位移曲线和刚度位移曲线

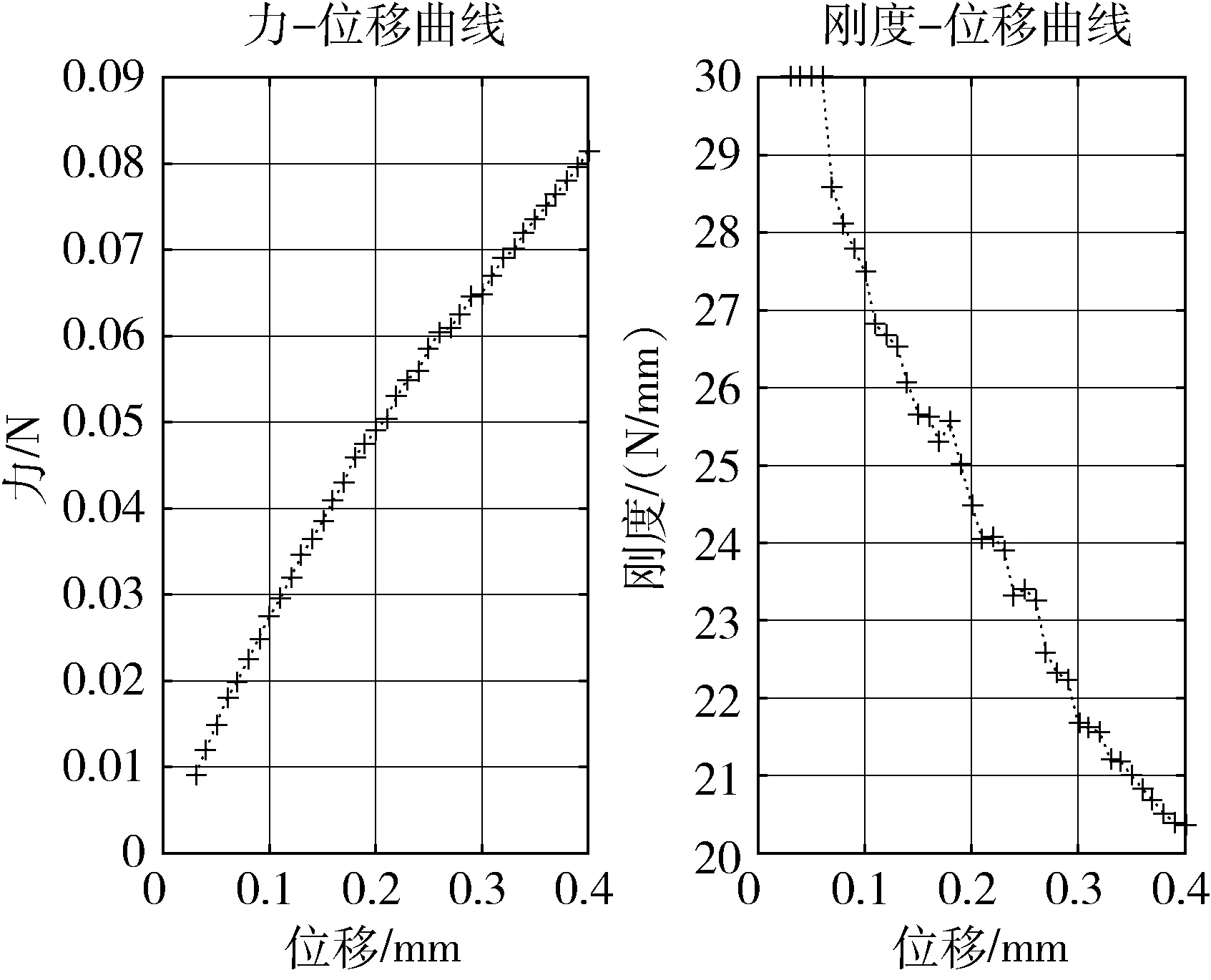
图4 弧形外壁力位移曲线和刚度位移曲线

图5 侧向外壁力位移曲线和刚度位移曲线

测试结果表明，香蒲杆外壁各向弯曲刚度中平形外壁受压刚度最低，弧形外壁受压刚度较高且刚度值在各位移处皆大于平形外壁受压刚度，侧面受压刚度最高且刚度值在各位移处为弧形外壁受压刚度的2～3倍.此外，平形外壁法向受压刚度、侧面受压刚度随着位移的增加有升高趋势，弧形外壁受压刚度随着位移的增加则有降低趋势.

1.2 轻质高刚仿生杆结构

根据香蒲杆结构特征，首先建立如图6所示半圆形仿生香蒲杆结构，单位为毫米.其次，根据前节力学测试结果，为避免使用平形壁面特征，利用香蒲杆弧形外壁、侧向外壁弯曲刚度较高的特点，采用平形外壁对扣的形式建立圆形截面仿生杆结构，将对扣重合壁面厚度设计为0.2 mm的隔膜，与横向膜、纵向膜厚度一致，如图7所示.

图6 半圆形截面轻质高刚仿生杆结构示意图

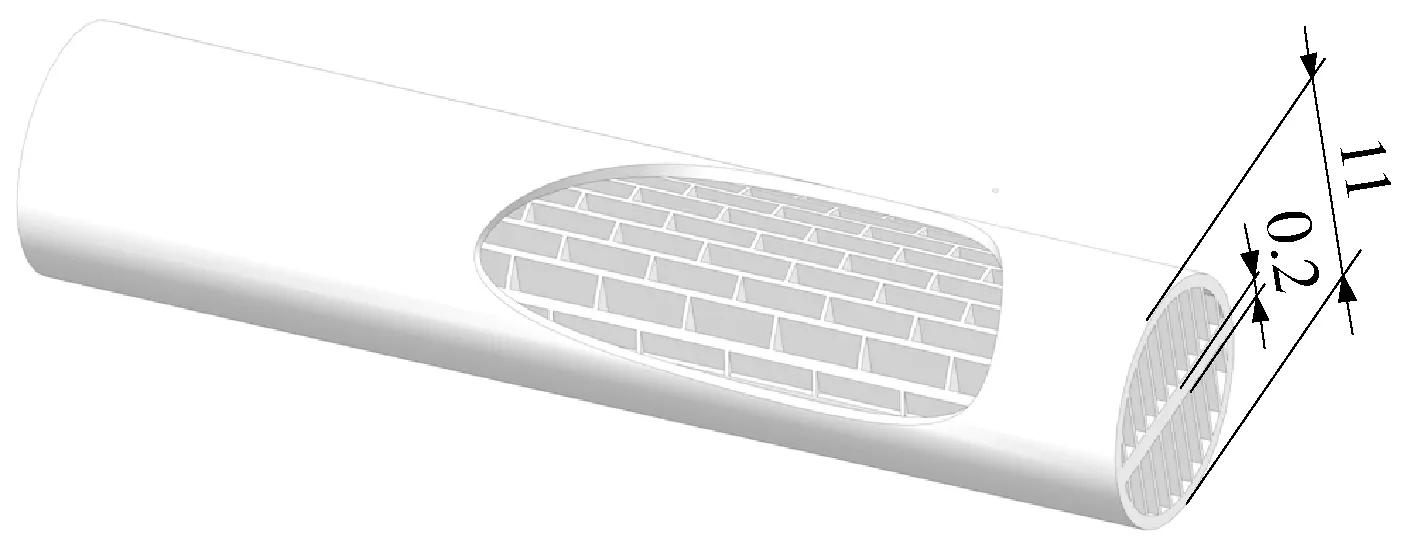
图7 圆形截面轻质高刚仿生杆结构示意图

为考察圆形截面仿生杆的弯曲刚度，将其与空心圆管结构作对比.取仿生杆与空心圆管的长度、质量、外径皆相等，计算得空心圆管壁厚约为1.29 mm.在有限元仿真软件中取材料为铝合金7075-T6，对长度皆为100 mm的两种杆模型一端端面全约束，另一端端面施加值为10 N且垂直于杆轴线的力载荷，分析结果如图8～13所示.

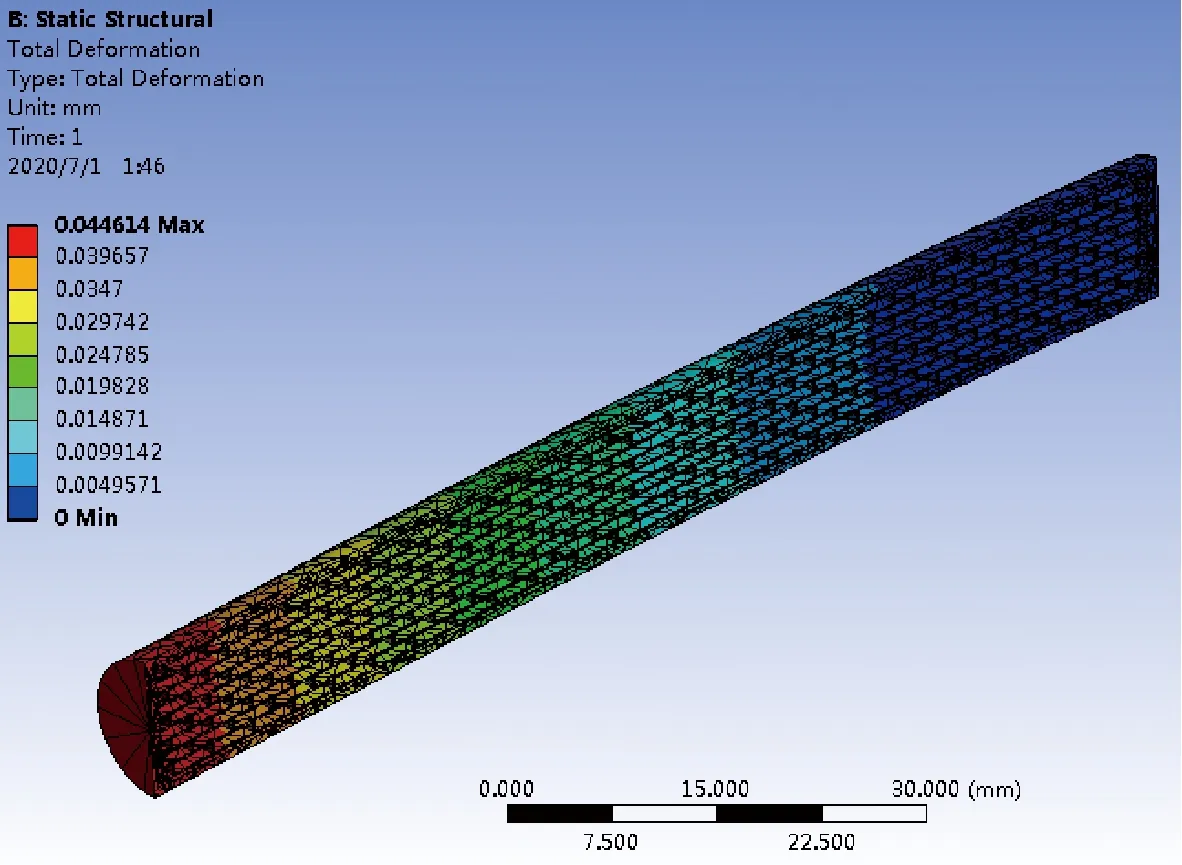
图8 仿生杆变形云图

图9 空心圆管变形云图

图10 仿生杆应变云图

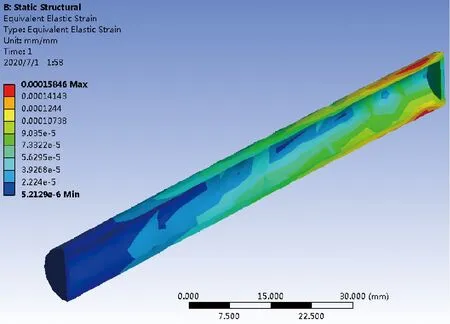
图11 空心圆管应变云图

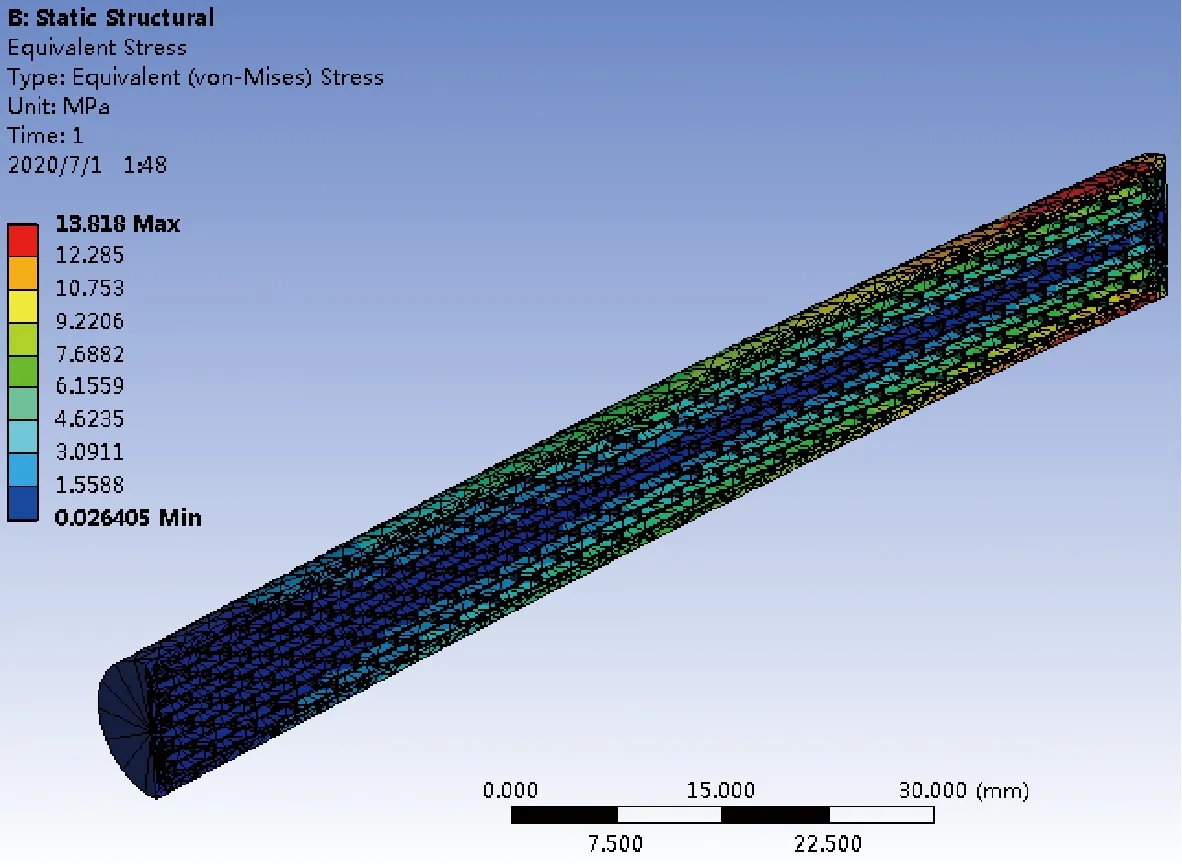
图12 仿生杆应力云图

图13 空心圆管应力云图

仿真结果表明，10 N载荷下仿生杆末端最大位移、最大应变、最大应力分别为空心圆管结构的0.46倍、0.44倍和1.23倍，仿生杆弯曲刚度约为空心圆管的2.2倍.

综上，仿生杆结构具有多腔体结构，质量轻、刚度高的优良特性，将在空间展开机构等以臂杆件为主的各类空间机构中具有广泛应用前景.本文将以对电磁力平衡传感器中精密柔性机构的分析为例，进一步开展仿生杆在柔性机构中的应用研究.

2 刚性、柔性精密机构分析

2.1 刚性平行四杆机构

电磁力平衡传感器的机构中的罗伯威尔机构的主构型为平行四杆机构，图14所示为一种由连杆机械铰链构成的刚性平行四杆机构，其中杆4、杆2、杆3和带载荷梁的连杆1组成一个平行四边形，载荷G放在载荷梁上，电磁平衡力F施加在连杆1的延伸杆上，则电磁平衡力F和载荷G的大小相等，此关系与二者具体的作用位置R、Δ无关，就此文献[7-10]已经证明，这里不再赘述.

图14 刚性平行四杆机构及其受力分析

若四边形ABCD不是严格平行四边形，将产生测量误差，记为形状误差.刚性杆件通过机械铰链连接，由于装配误差及配合间隙的存在，形状误差较大，限制了传感器的测量精度.

2.2 柔性平行四杆机构受力分析

如图15所示，以直圆型柔性铰链为例，柔性平行四杆机构在任意平衡位置对杆件1列力、绕A点的力矩平衡方程：

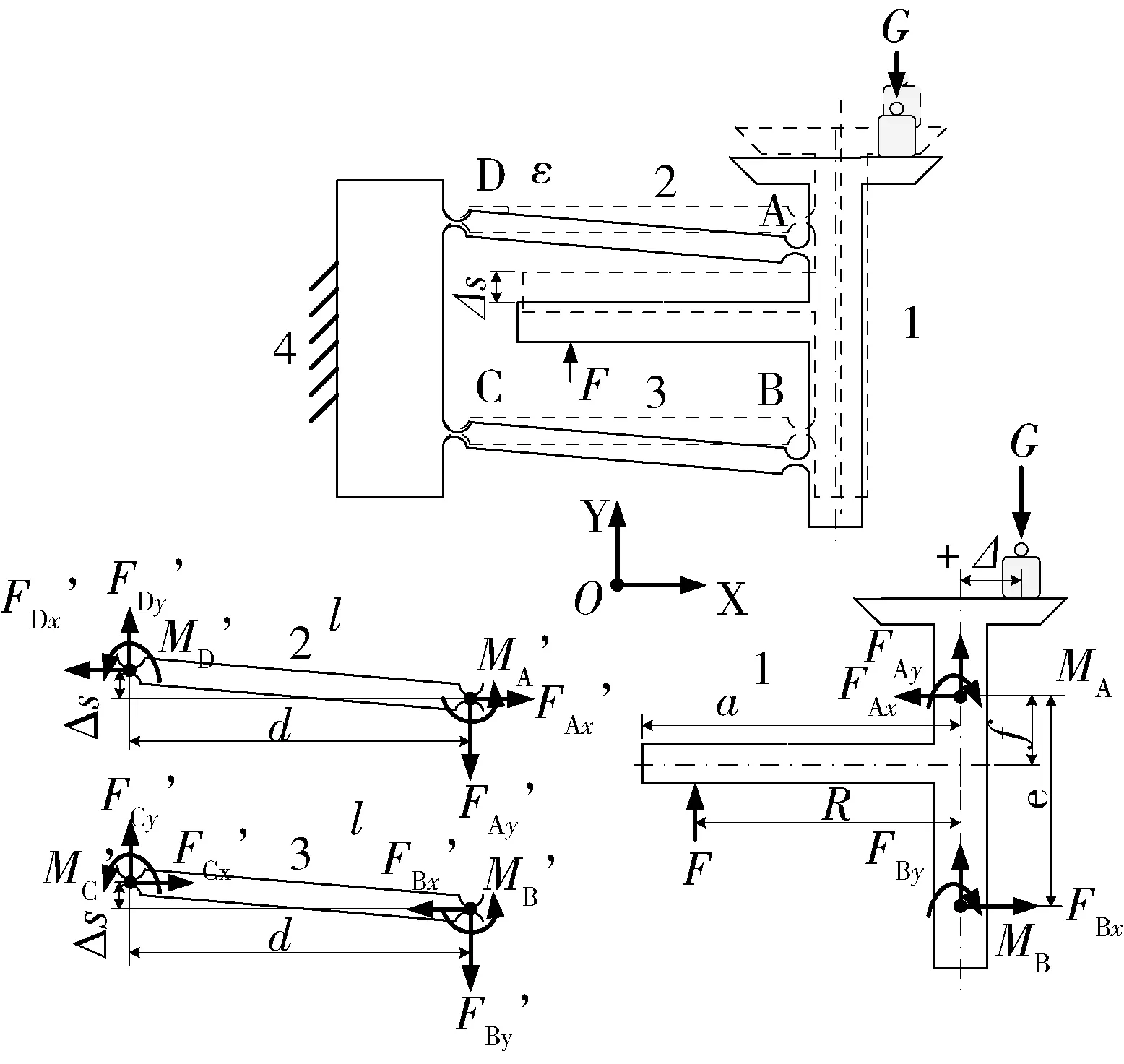
图15 柔性平行四杆机构及其受力分析

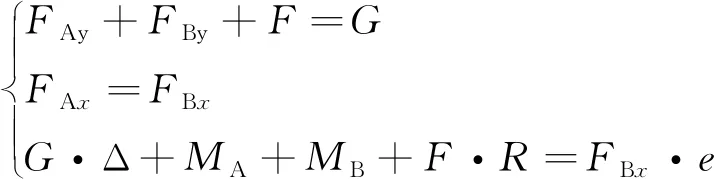
(1)

分别对杆件2、3的D、C点列力矩平衡方程：

(2)

假设受载后平行四边形4个柔性铰链的转角大小相等，结合作用力与反作用力大小相等得边界条件

(3)

联立方程组(1)、(2)、(3)解得杆件1的受力情况

(4)

式(4)中第一个式子即为被测载荷的表达式，ΔF为载荷的测量误差.

连杆1Y方向位移为Δs时，铰链A、B、C、D的转角ε和弯矩M分别为[11]

(5)

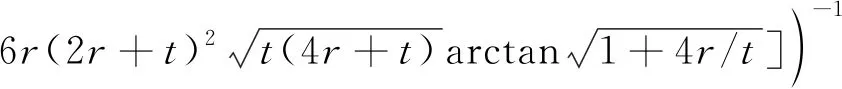
(6)

其中，E为弹性模量，r为铰链半径，w为铰链宽度，t为铰链厚度.

2.3 误差分析

(1)设位置传感器的检测误差为Δs，将式(5)、(6)代入式(4)得载荷质量的测量误差Δm为

[t(4r+t)·(6r2+4rt+t2)+6r(2r+t)2·

(7)

取机构参数E=71.7×109Pa、t=0.15 mm、r=2.925 mm、w=10 mm、l=125.075 mm、g=9.8 N/kg，Δs和Δm之间的关系如图16，可知若位移检测误差为0.5×10-6m，则传感器质量测量误差约为3×10-2g.

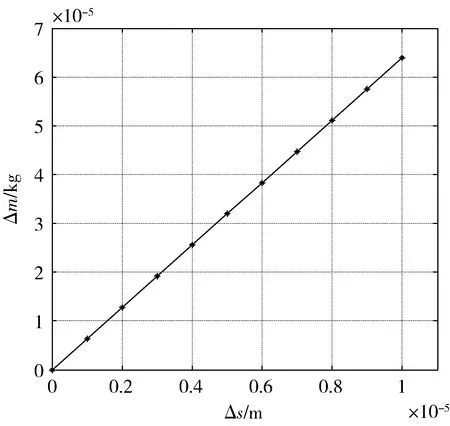
图16 Δm与Δs关系

特别地，只有当平衡力F使得柔性平行四杆机构在初始位置处平衡即Δs=0时，才有F=G即电磁平衡力等于被测载荷自身的重力.

(2)由于被测件在载荷梁上的放置位置是随机的，通常平衡力F和载荷G的作用线不重合，由前节分析知此时铰链所受轴向力Fx不为零，轴向力引起的轴向位移量Δx使杆1发生一定偏转角γ，从而起杆1末端Y向的位置检测误差Δs，如图17所示.

图17 柔性平行四杆机构中铰链变形Δx及其引起的位置误差Δs

机构中取f=e/2，平衡力F与载荷G对杆1作用的合力矩MF,G=FΔ+GR，由式(4)得铰链A、B、C、D初始平衡位置处的轴向位移Δx为[11]

(8)

杆1末端Y向的位置检测误差Δs为

(9)

取参数a=120 mm、R=80 mm、e=60 mm，其余参数同上，MF,G和Δm关系如图18，可知若F与G对杆1的合力矩为80 g·cm，则传感器质量测量误差约为1.2×10-4g.

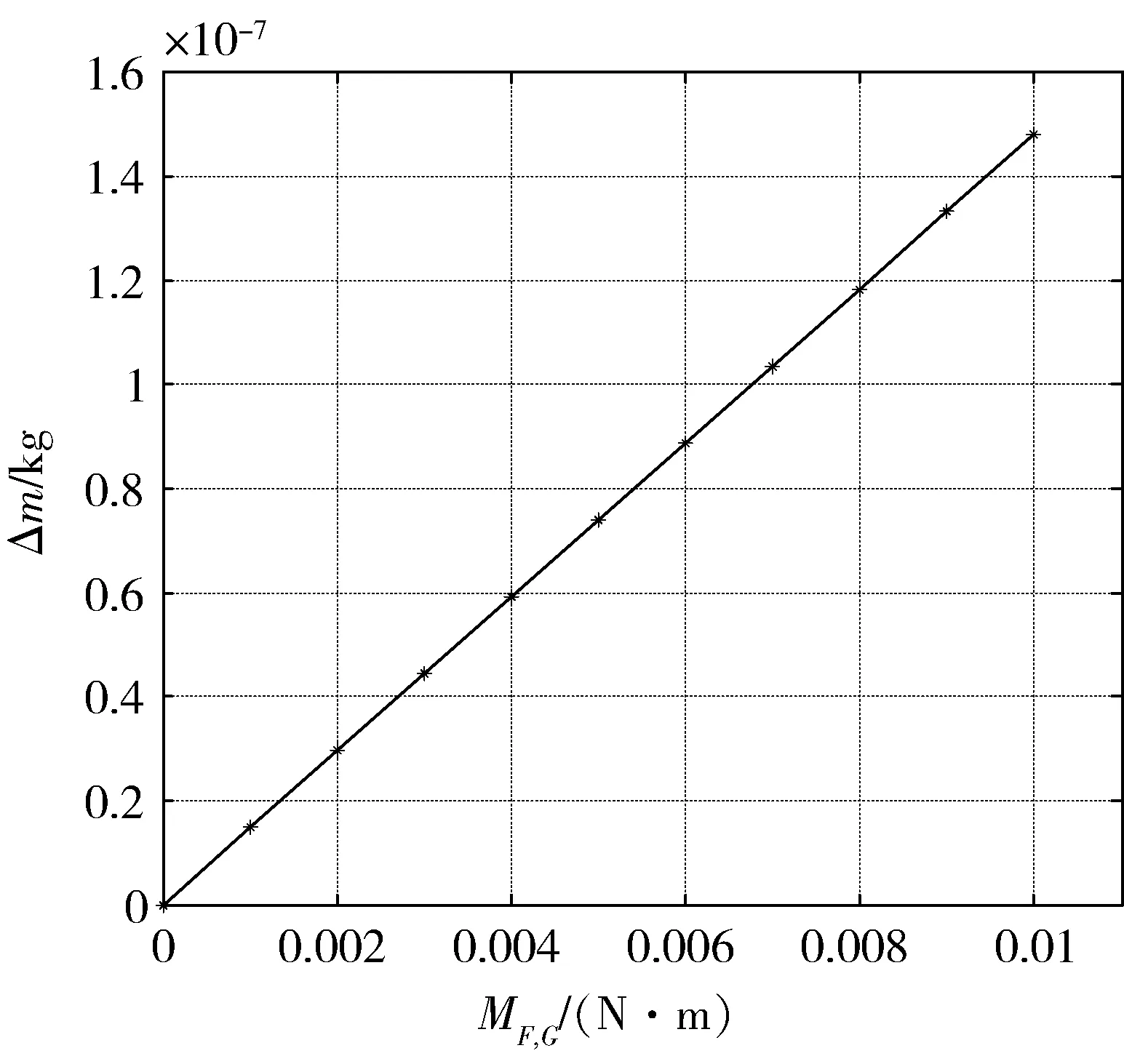
图18 Δm与MF,G关系

图19 直圆型柔性铰链

αZ=CMMZ-CFYFY

(10)

式中，CFY、CM分别为切向力柔度和弯矩柔度，二者取值为[11]

令铰链转角为零，得：

MZ=rFY

(11)

式(11)即直圆型柔性铰链只发生平移运动的载荷条件.

单个矢量力的平移将引入力矩，由式(11)可知当切向力FY作用在直圆型柔性铰链长度的中点位置时，铰链轴向位移Δx为零，绕Z轴转角θZ为零，铰链将只发生Y方向的平移运动[14]，如图20所示.

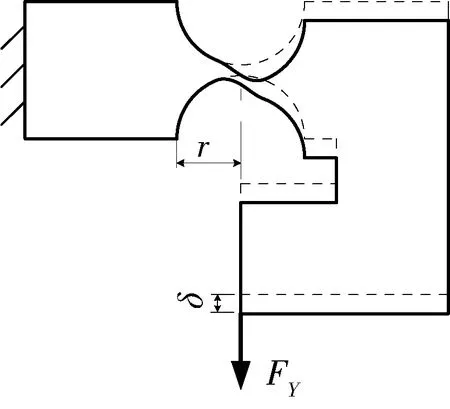
图20 铰链平移运动载荷条件

同理，对于柔性平行四杆机构，如图21所示，被测载荷G为一种切向载荷，当G的作用线通过杆2(或杆3)长度的中点时，杆1将只发生Y向的平移运动，此时杆1延伸杆末端Y向的检测位移δ不含由杆1倾斜引起的误差Δs.

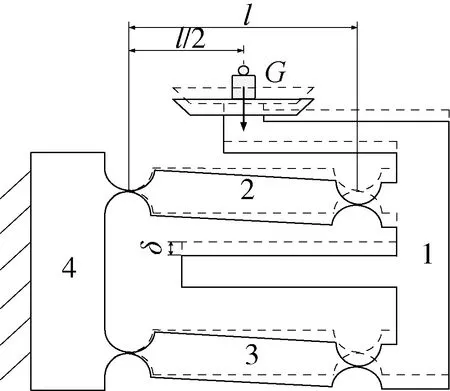
图21 柔性平行四杆机构不引入位移检测误差的载荷条件

因此，通过使载荷梁中心的位置尽量靠近杆2(或杆3)的中点可有效减小传感器动态调整过程中Y向位移δ的检测误差，缩短系统调整时间.进而，通过使电磁力驱动力F的作用线与外载荷G的作用线共线，则二者形成的合力矩将为零，由连杆1转角γ引起的位移δ的检测误差将为零，从而有效提高传感器对质量测量的精度.

3 有限元仿真及分析

采用圆形截面轻质高刚仿生杆为主要承力结构，直圆缺口型铰链为柔性转动单元，对柔性转动单元两端预留轴向5 mm长度的实心材料作为过渡，建立初始位置处平衡的柔性平行四杆机构有限元模型，如图22所示.取铰链参数E=71.7×109Pa、t=0.15 mm、r=2.925 mm、w=11 mm，机构参数l=120 mm、a=80 mm、R=60 mm、e=60 mm、f=0.5e，模型材料取铝合金7075-T6，载荷条件取F=G=0.5 N，令载荷偏距Δ从-l/2到50 mm每间隔5 mm取值分别加载.仿真结果表明，仿生杆部位受力均匀，机构最大应力约为0.63 MPa，如图23所示，最大应变约为9.14×10-6mm，如图24所示，均发生在杆1延伸杆直角根部附近，此位置为圆柱相贯线，属局部应力集中现象，可通过倒角等方式对结构优化.

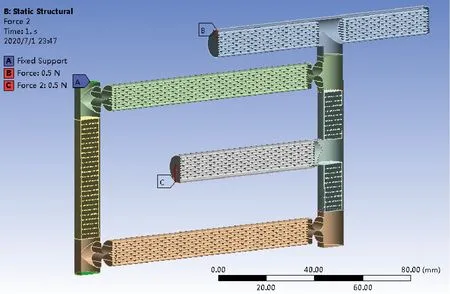
图22 采用仿生杆的柔性机构有限元模型

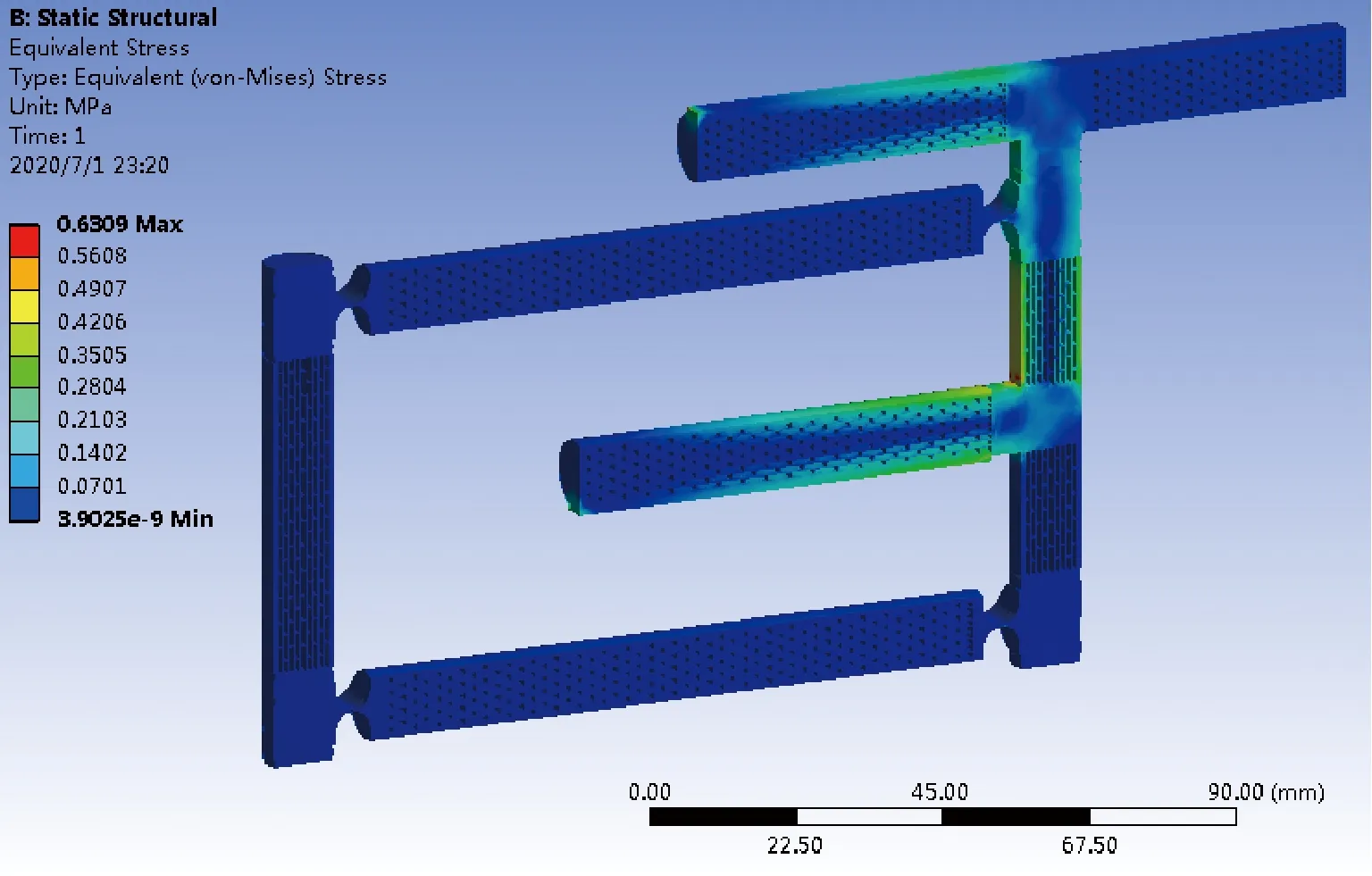
图23 采用仿生杆的柔性机构应力分布云图

图24 采用仿生杆的柔性机构应变分布云图

如图14所示，在有限元仿真中保持Y向载荷G=0.5 N的大小不变，其作用位置随Δ变化，杆1延伸杆R处施加反向驱动力F，调整F的大小使水平杆2、3达到初始水平位置时(取误差≤±2 nm，根据位移检测精度而定)计算F与G的差.如图25所示，仿真结果表明当Δ=50 mm时F和G相距最远，F和G最大相差1.9×10-5N，相对误差为0.0038%.随着载荷G的位置向杆2的中点(Δ=-l/2处)靠近，F和G的差在不断减小并在杆2中点附近取得零值.

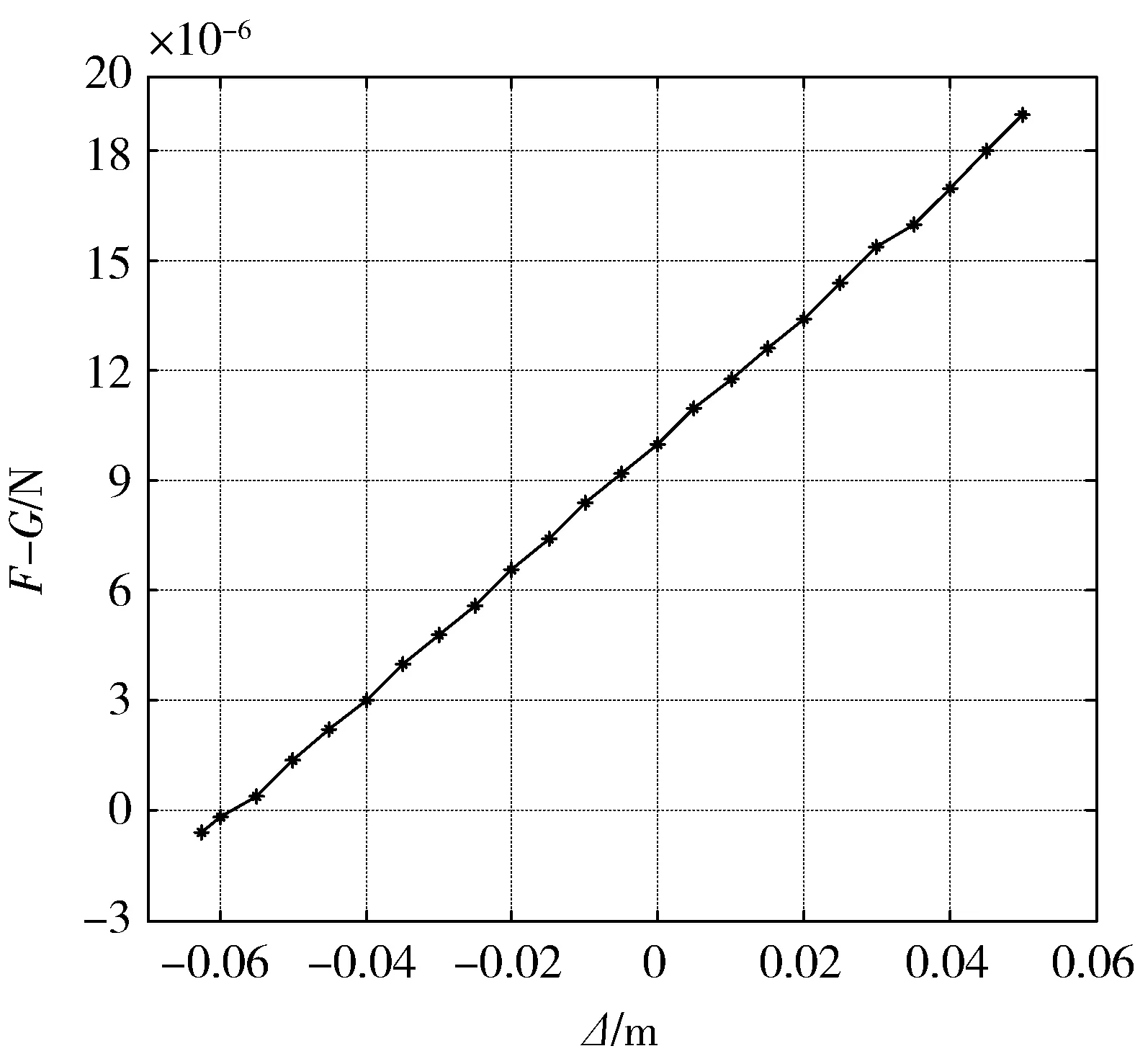
图25 F与G的差随Δ变化的有限元仿真

4 结 论

柔性罗伯威尔机构力学分析中假设柔性平行四杆机构的4个柔性铰链内弯矩是相等的，而实际由于轴向力FX的存在，铰链X向微小变形Δx使得杆2被拉长杆3被压短，机构并非严格意义的平行四边形，导致四个铰链间内弯矩的不等，故该假设会产生微小误差.同理，对柔性铰链Y向微小变形Δy进行了忽略，实际杆1(或杆4)两个铰链所受Y向力是大小相等方向相反的，这导致两个铰链的Y向位移Δy大小相等方向相反，从而使杆1被压短杆4被拉长，也会引起平行四边形一定程度的变形，从而引入微小误差.通过合理设计柔性铰链参数(例如宽度w)可以减小铰链变形进而降低此类机构形状误差引起的测量误差.

仿生杆结构特点为多腔体薄壁结构，尺寸在毫米级，基于目前的技术水平，仿生结构可采用3D打印技术实现.针对空间应用背景，在结构设计和制作过程考虑放气孔或真空制造工艺.关于仿生机构发射过程遇到的力学振动和冲击，可通过结构设计提高机构自身刚度或采取外部减震措施等方法解决.

本文通过有限元仿真分析，对比了仿生杆和空心圆管的弯曲刚度，以仿生杆为承力结构构建了一种精密柔性机构，并对机构进行了误差分析.基于仿香蒲杆结构的圆形截面仿生杆，其弯曲刚度明显优于等长度、等外径、等质量的空心圆管，圆形截面仿生杆具有质量轻、刚度高的优点，其在空间大型天线展开机构、空间站大型操作臂等领域具有广泛的应用前景.采用圆形截面仿生杆构建的柔性机构载荷测量的最大相对误差为0.0038%，机构力学性能优良，仿生杆作为承力结构可用于构建精密柔性机构.