浅析整体法和隔离法在高中物理教学中的应用研究

寇 娥

(甘肃省民乐县第一中学 734500)

物理作为具有较强生活性的一门学科，通过物理知识的学习，通常能够使学生更好的理解与掌握实际生活中存有的物理现象.高中物理的内容中，力学通常是重点，不论是课程的安排，还是考试中的占比，都能体现出该知识点.在对力学问题进行解决时，常规思路就是与已知条件相结合分析受力情况，明确物体的实际受力状况，以形成构造力学的等式，也就是隔离法处理，对于部分的物理问题而言，物理受力的状况通常极为复杂，若拆分了受力系统，就会造成相应的干扰项，并影响到学生自身的判断，因此，在处理相关物理问题的时候，需试着将系统看作成整体，也就是整体法.因此，高中物理的课堂教学中，教师需注重整体法与隔离法的渗透，以促进学生的思维发展以及解题过程的优化.

1 整体法与隔离法概述

1.1 整体法

1.1.1 整体法内涵

整体法主要是将几个物体当做是个整体，或者将看着有明显的不同特点与性质的物理过程当做整体进行处理.对于整体法而言，是高中物理教学中常用的基本方法，也是研究物理教学整体系统或过程开展的分析与研究方法.力学的学习中，则是将几个物体当做成一个整体，将当做研究对象进行受力分析，只是对整体对象以外的物体对于整体呈现的作用力(外力)进行分析，而不用考虑其内部中的互相作用力(内力).

1.1.2 整体法选用原则

整体法的运用不是很广泛，并非所有平衡问题与动力学都能通过整体法进行研究.通常来说，求解问题符合下述几种情况的时候，则能通过整体法运用原则：(1)相同性质物体作为研究对象来解决物理问题.(2)不受到其他细节干扰，系统的解决单一物理问题.(3)运用物理规律解释应用系统问题，如整体受力分析、动量定理、机械能量守恒定律等.(4)涉及到多个物体或多个过程作为一个整体来研究，一般采用整体法，例如：平衡状态需要系统分析外力，而非系统内部各种物体之间的互相作用，也就是内力；突出主要的矛盾，也就是研究的外力，并避开其次要矛盾，也就是系统内力.其优点是帮学生理清一个系统完整的受力情况，及整个运用过程，从整体视角出发揭示事物的变化规律.避免中间过程的复杂分析，有利于更准确解决物理问题.

1.1.3 整体法解题的步骤

(1)将研究对象看做一个整体，对整个受力分析，避免分析系统内部之间的力；

(2)分析除整体以外的物体，对整体所施加的作用力，或者对运动过程实施分析；

(3)建立多种思维模式，体现一种综合性思维，重视知识的综合和思维组合，整体思维不仅建立在理论性较强，具有较高的物理研究价值，还需要运用整体思维研究分析.

1.2 隔离法

1.2.1 隔离法内涵

隔离法主要指把研究对象由周围环境当中隔离出来实施单独研究，该研究对象既能是个物体，也能是物体的某个部分，广义上讲，隔离法还包含了将物理过程由整个过程隔离.同时，隔离法还是指对物理问题当中单个物体或者单个过程实施分析与研究的一种方法，将其运用于力学中，则是将分析的物体由有关物体体系当中隔离，将其当作研究对象，分析研究对象之外的物体对于该对象形成的作用力，而不考虑具体研究对象对于其他的物体形成的作用力.

1.2.2 隔离法选用原则

隔离法的应用通常较为广泛，大部分是力学问题，将研究对象从系统中隔离出来系统分析，或是将研究过程从整体过程中隔离出来分析.通常物理模型运用到隔离法可以有效解决教学难题，但是由于复杂且繁琐的计算过程，为解题带来不小的难度.为此，在选用隔离法解决物理模式时应当注意以下几点原则.(1)将某个过程从整体过程中分离出来，如果求解目标是某一个过程中间的物理量，从这个状态中提取后分析.(2)求解目标当中某个运动物体出现的变化.(3)研究系统内部物体之间存在相互作用，求解系统当中某个具体运动规律.

1.2.3 隔离法解题的步骤

(1)研究对象从周围环境中隔离出来单独分析，这个研究对象可以是物体，也可以是物体的一部分.

(2)将一个物理过程从其过程中全部隔离出来.

(3)求解对象之间计算内力或者加速度，优先选择隔离法.

(4)挖掘已知的物理量与未知的物理量的隐含关系，并选择相应的物理规律，列出对应的方程并加以求解.其运用优点是容易看清单一物体的运动情况，清楚了解每个物体在每段过程里的运动状况.利于将复杂的物理题目简单化、单一化.与此同时，隔离法在教学中便于学生掌握，适合物理知识初学者应用.

2 整体法和隔离法在高中物理教学中的应用策略

2.1 多物体整体

单一物体形成的系统，可以根据牛顿第二定律写为F=ma，而两个或者两个以上的物体形成的系统，当系统中各物体加速度各不相同，牛顿第二定律依然适用，即能写为：F=m1a1+m2a2+m3a3+m4a4…+mnan.

2.1.1 应用于平衡状态中

例如，如图1可知，质量分别是m1、m2的两个物体经过轻质弹簧进行连接，通过力F的作用，沿着水平方向进行匀速直线的运动，且m1在地面，而m2在空中，同时力F和水平方向呈现θ角，那么，m1所受到的支持力FN与摩擦力f是正确关系的为( ).

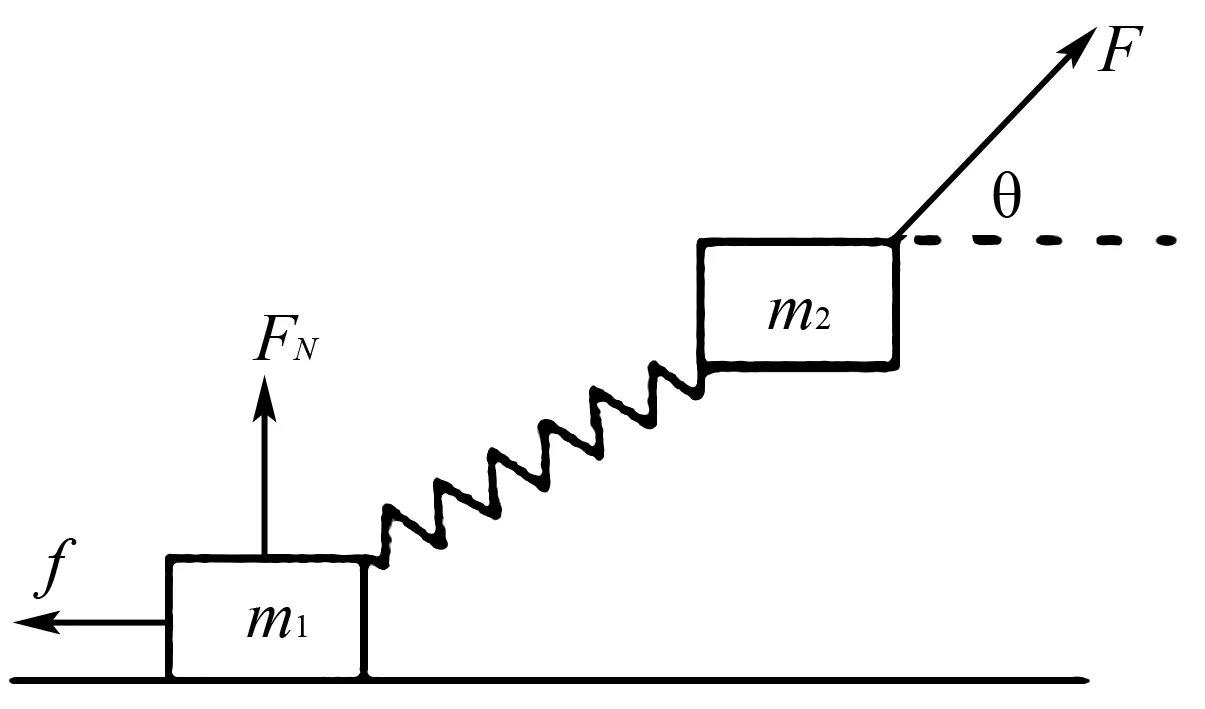
图1

A.FN=m1g+m2g-Fsinθ

B.FN=m1g+m2g-Fcosθ

C.f=Fcosθ

D.f=Fsinθ

解析本题解题法为整体法.答案：AC

2.1.2 应用于牛顿运动定律中

例如，如图2可知，光滑的水平面上放着质量是m与2m的四块木块，其中，由两个的质量是m的木块中间通过不能伸长的轻绳进行连接，且木块之间最大的静摩擦力是μmg，现在通过水平拉力F拉一个质量是2m的木块，将四个木块通过相同速度进行运动，轻绳对m的拉力最大是( ).

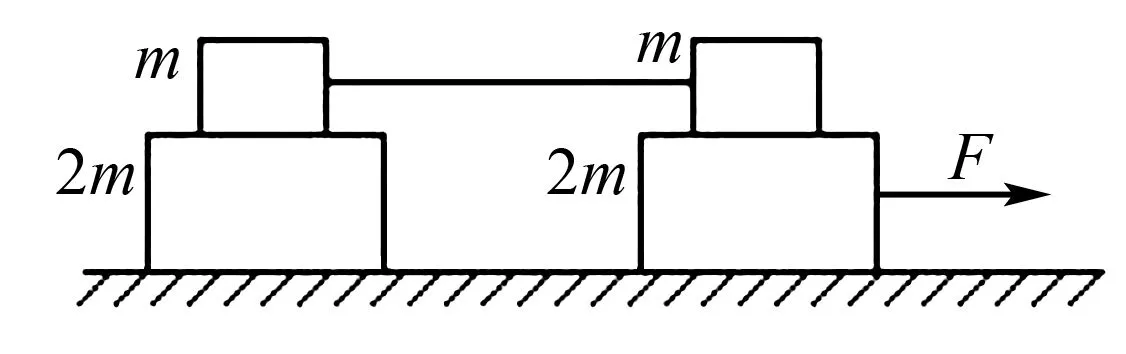
图2

A.3μmg/5 B.3μmg/4 C.3μmg/2 D.3μmg

答案：B

2.2 多过程整体

在遇到物理习题中涉及到多个运动过程的题型，应当采用隔离法先拆分过程，就能找出其遵循的规律，如机械能守恒、动量守恒的定律，因此，教师可引导学生将其视为一个整体，一次性列出方程解答，这样能够省略中间过程，而且还能防止解很多的方程，以促使学生的解题效率与速度得到切实提高.

例如，质量是M、内壁间距是L的箱子处于光滑的水平面，箱子的中间有个质量是m的小物块，箱子地板与小物块之间的动摩擦是μ，在初始时候，小物块停留于箱子的正中间，如图3，现给出小物块水平朝右的初速度是v，小物块和箱壁经过N次碰撞后，又会回到箱子的正中间，与箱子呈相对静止.假设碰撞都存有弹性，在这个过程中，系统所损失掉的动能是( ).

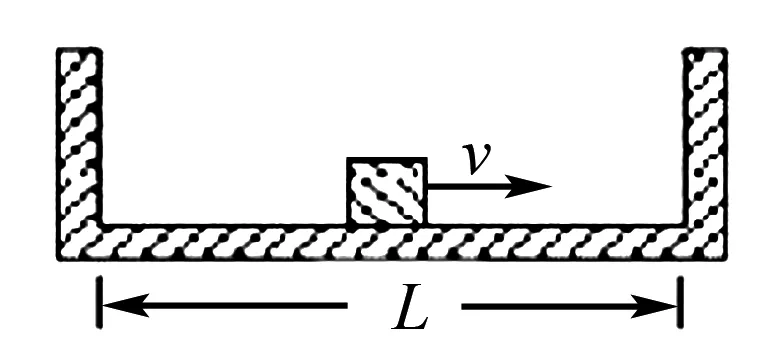
图3

A.mv2/2 B.(mM)/2(m+M)v2

C.NμmgL/2 D.NμmgL

将N次的碰撞看作为整体，在具体解题的时候，就不需要考虑中间的碰撞细节，只有找出系统化初、末的状态，就能有效简化问题.答案：BD.

3 整体法与隔离法运用的应用要点

在处理物理问题是，不能孤立看待整体法或隔离法，两者在解题思路上看似相互相对立，但又形成统一关系，由实际问题的具体情况作为出发点，灵活的选择研究对象，合理的选择应用的方法.大部分题目都要求综合运用两种方法，实际应用顺序也比较固定，也就是求取外力的时候，先隔离再整体；求取内力的时候，则是先整体，再隔离，不论是哪种，都是为了求解出共同加速度.

综上所述，整体法更加注重对整体系统和外界环境的相互作用进行分析，而忽视了系统内的物体见互相作用的关系，这种处理问题，能够更直观的看出物理量的关系，但却无法理清楚系统中物体内部的作用关系.以此为基础，就能通过隔离法进行问题解决，通过整体法进行补充，因此，在物理问题的解决时，如物理试题是求取外力，则优先选择整体法；如物理试题是求取内力，则需优先选择隔离法，从而使学生实现高效解题.