“双减”背景下 让实验教学走进中职数学课堂——中职数学圆中最值问题初探

谢小云

(福建省武平职业中专学校 364399)

当下，国家大力发展职业教育，教师面对数学基础普遍较差，学习数学兴趣普遍不高的中职学生，遇到了很大挑战，为了提高课堂效率，提高学生动手能力、思维能力、探究能力，本人用实验教学方法探究数学问题，揭示数学问题本质.日常教学中，我们常常把圆看作是静态的，如果把动点放在图形上，静态圆就变成动态圆，这样就构成了栩栩如生的数学问题，让学生乐于探究，教学方法也由传统的满堂灌教学法变成了研究性学习.

1 点与圆的最值问题探究

实验一：已知圆C：(x-4)2+(y-2)2=1及点P(-1，0)，在圆C上求一点A，使AP最长或最短.

实验目的：掌握圆外一点到圆上一点最值求法，培养分析问题和解决问题能力.

实验用到的公式：两点间距离公式.

实验教具：细线、直尺、A4纸、圆规、图钉.

实验方法：让学生在A4纸上画出圆C及点P位置，用图钉把细线的一端固定在P点，拉直直线，让另一端点A在圆C上移动，注意观察线段PA长度的变化并测出PA的长度.

实验图像：动点A以线段PC与圆交点D为出发点顺时针方向匀速运动一周，以动点A的运动时间为横坐标，PA长度为纵坐标画出图像.

实验误差及分析：所作的图形不准确以及肉眼观察与真实数据差异.

图1 图2

实验结论及分析：如图1，连结线段PC与圆C相交于点A，设点B是圆上异于A点的任意一点，则PB+BC≥PC=AC+PA，因为圆的半径相等即AC=BC,所以PB≥PA，此时PA最短；如图2，延长线段PC交圆C于点A，设点D是圆C上异于点A的任意一点，连结CD及PD，在△PCD中，PC+CD≥PD，又因为CD=CA，所以PC+CA≥PD即PA≥PD，此时PA最长.

通过上述实验教学，学生直观形象地得出圆外一点到圆上一点最值问题与圆心和半径有关，即PAmax=PC+r，PAmin=PC-r(r为圆C的半径)，面对数学基础较差的中职学生，圆的最值问题既是重点也是难点又往往是会考考点，教学时让学生自己动手实验，可起到事半功倍的效果.

2 直线和圆的最值问题探究

实验二：已知圆C：(x-3)2+(y-4)2=1，直线L：y=x+5,求圆上一点A到直线L的距离最大值和最小值.

实验目的：让学生掌握圆上一点P(x0,y0) 到直线距离最值求法及转化数学思想.

实验用到的数学公式：点到直线的距离公式.

实验误差分析：所作的图形不准确以及肉眼观察与真实数据差异,另外三角板起始刻度不在边上，要把无刻度这部分重新计算也增加误差.

实验用具：A4纸、三角板

实验过程及方法：让三角板的一条直角边紧靠直线L，另一条直角边与圆C相交于点A，与直线L相交于点P，仔细观察PA长度的变化规律.

实验图像：当直角边过圆心与圆相交于A、B两点，动点D从A点出发顺时针方向匀速运动一周，以动点D的运动时间为横坐标，PA长度为纵坐标画出图像.

实验结论：如图3，当三角板的另一条直角边过点C时，线段PC的延长线与圆相交于点A，此时PA最长.如图4，当线段PC与圆相交于点A时.此时PA最短，即PAmax=|PC|+r,PAmin=|PC|-r(r为圆C的半径)，圆上一点到直线L的距离的最值仍然与圆心和半径有关.

图3 图4

实验分析：如图4，设点D是圆上异于A、B点的任意一点，连结PD、DA、DC，在三角形PCD中PD+DC≥PC，又因为PC=PA+AC，DC=AC所以PD≥PA，如图3，设点D是圆上异于A点的任意一点,在三角形PCD中PC+CD≥PD,又因为CA=CD，所以PC+CA≥PD,即PA≥PD,结论成立.

实验改进与启发：可以自制三角板，刻度从边上开始计算.

实验目的：让学生掌握过圆内一点最短弦长求法及数形结合数学思想.

实验用具：A4纸、三角板、图钉、直尺

实验过程及方法：让直尺中某一点紧靠P点，绕点P旋转直尺一周，与圆相交于AB，观察AB长度的变化规律.

实验误差分析：所作的图形不准确以及肉眼观察与真实数据差异,另外，A、B两点都是动点，给测量带来难度.

实验创新：鼓励学生大胆改进实验，容易测出AB长度.

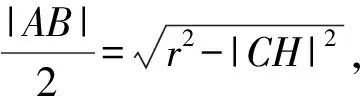
3 圆与圆的最值问题探究

实验四：“将军饮马”问题，已知点C1(3,4)、C2(-2,2)，在x轴上找一点P，使|PC1|+|PC2|最短.

实验目的：让学生掌握直线上一动点到两定点距离最短求法及数形结合数学思想.

实验用到的公式：两点间距离公式及对称数学思想.

实验用具：A4纸、图钉、细线、直尺

实验过程及方法：在A4纸上画出所需图形，用图钉把细线一端固定于C1点，细线上一动点P在x轴上移动，另一点C2也在细线上移动，仔细观察|PC1|+|PC2|的长度变化.

实验结论：如图5，过点C2作关于x轴的对称点C0，连结C0C1与x轴交于点P，则点P就是所求的点.

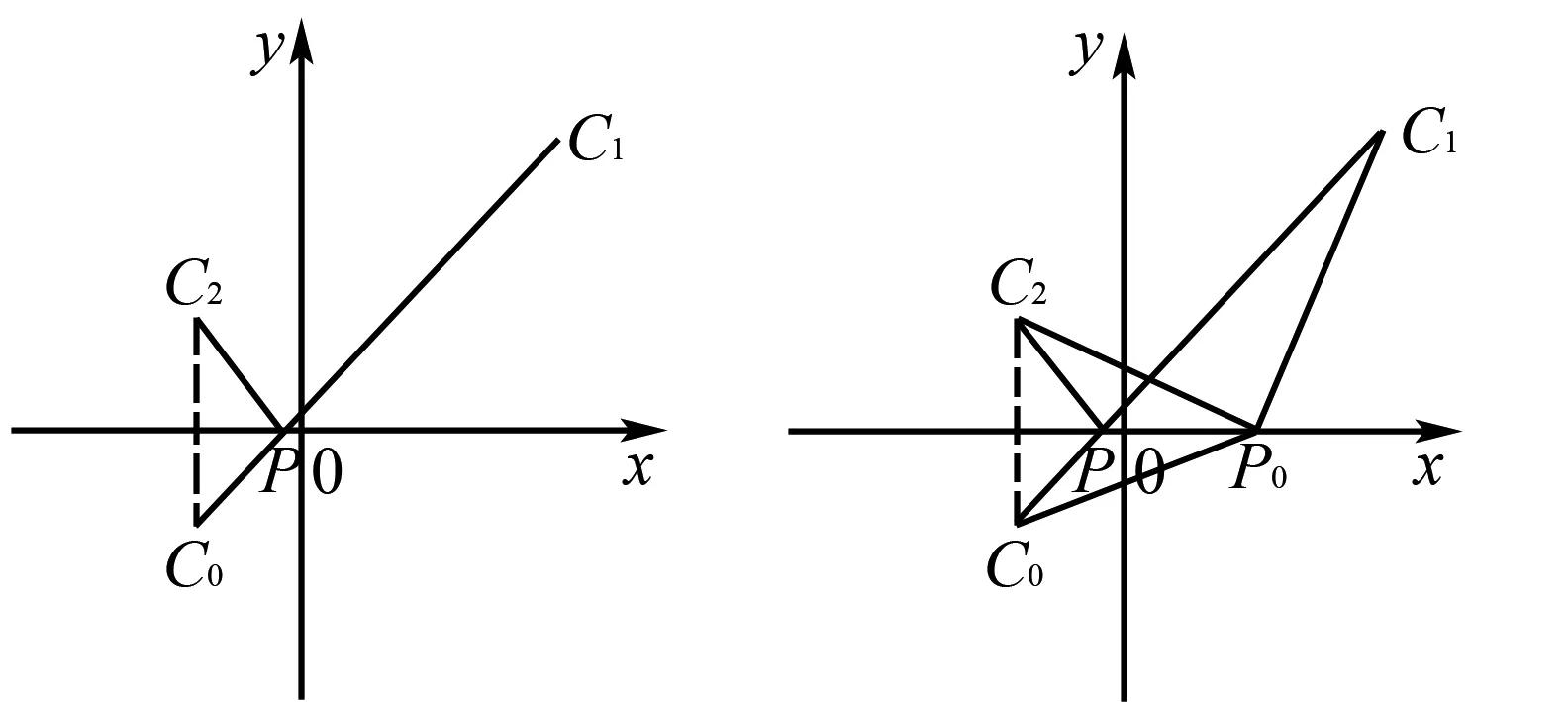
图5 图6

分析实验结果：如图6，设点P0是x轴上任意一点，因为x轴是C2C0的中垂线，所以C2P0=C0P0,C2P=C0P,即PC2+PC1=PC0+PC1=C0C1，而P0C2+P0C1=P0C0+P0C1≥C0C1,所以P0C2+P0C1≥PC2+PC1，实验结论是成立的.

实验五：如图7，已知点C2(-2，2)及⊙C1：(x-3)2+(y-4)2=1，点A是⊙C1上动点，在x轴上找一点P，使|PA|+|PC2|最小.

实验用具：硬纸壳两张，图钉，胶水，细线，圆规，三角板，滑轮，大头针.

实验准备：用硬纸壳制作一个圆及凹形纸槽.

实验过程与方法：如图7，在硬纸壳上用大头针固定坐标轴及圆位置，纸槽固定在x轴，细线穿过滑轮一端固定在⊙C1上，另一点C2也在细线上，滑轮在纸槽上运动，顺时针旋转圆，仔细观察|PC1|+|PC2|的长度变化.

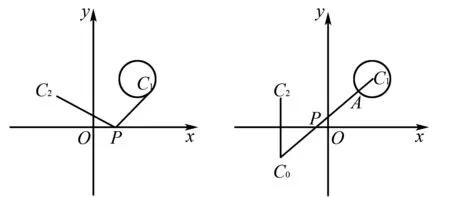
图7 图8

实验目的：让学生掌握在直线上找一点到一定点与圆上动点距离最短求法及数形结合数学思想.

实验误差分析：所作的图形不准确以及肉眼观察与真实数据差异,另外，A、P两点都是动点，给测量带来难度.

实验结论：如图8，过点C2作关于x轴的对称点C0，连结C0C1与x轴交于点P，此时|PC2|+|PC1|最小，所以|PC2|+|PA|=|PC2|+|PC1|-r.

分析实验结论：“以静制动”分析问题，首先考虑在x轴上找一点P1使|PC1|+|PC2|最短.此时A点就是PC1与⊙C1的交点，从而得出(|PC2|+|PA|)min=|PC2|+|PC1|-r.

实验改进：本实验较复杂，学生可以结合所学专业充分发挥想象空间，做出实用、精美教具，这样数学与所学专业就结合在一起了.

实验六：如图9，已知⊙C1(x-3)2+(y-4)2=1，圆C2：(x+2)2+(y-2)2=1,A、B两点分别为⊙C1及⊙C2上的动点，在x轴上找一点P，使|PA|+|PB|最小.

本实验可以让学生亲自动手制作，发挥学生主观能动性，培养学生创新能力.

图9 图10

实验分析:如图10，首先考虑在x轴上找一点P，使|PC1|+|PC2|最短,则|PA|+|PB|=|PC1|-r1+|PC2|-r2.

数学实验是探究问题本质非常有效的途径.数学实验探究过程要从简单到复杂，从现象到本质，在课堂上我们应该勤于动手，敢于动脑，勇于探究，大胆创新，在减负的背景下让实验教学走进课堂，提高学生核心素养，减轻学生负担.