含转动摩擦型干式梁-柱节点的新型装配式混凝土框架结构抗震性能研究

杨参天，李爱群,，贾军波

(1. 东南大学土木工程学院，南京 210096；2. 北京建筑大学土木与交通工程学院，北京 100044)

装配式预制混凝土(precast concrete, PC)结构体系被大量应用于各类建筑的建造，产生了良好的社会和经济效益[1-2]。在各类PC 结构中，PC框架结构常用于各类医院、校舍、办公楼等在城市中具有重要功能的建筑物，其抗震安全是影响城市综合灾害抵御能力的重要因素。梁-柱节点是决定PC 框架结构抗震性能的关键，按照现场装配是否需要浇筑混凝土，可分为湿式和干式两类节点[3-5]。其中，干式节点具有施工效率高和绿色环保的特点，是建筑工业化的发展方向之一，也是装配式结构领域的研究热点。因此，干式装配梁-柱节点的创新发展和相关研究具有重要意义。

国内外学者提出了各类干式装配梁-柱节点的构造形式。美国和日本联合开展的PRESSS 项目[6]提出了预应力装配式梁-柱节点，通过节点试验研究验证了其力学性能，提出了相关设计方法，并在工程实践中应用推广。Hanaor 等[7]提出了一种采用预应力螺栓的装配式梁柱节点，可实现刚性和半刚性连接，并开展了试验研究，提出了节点简化设计方法。郭彤等[8]提出了腹板摩擦式自定心预应力混凝土框架梁柱节点，试验研究表明：该节点具有震后自复位、主体结构基本无损、耗能机制明确等优点。Morgen 等[9]提出了一种基于摩擦耗能装置的装配式梁-柱节点，开展了节点和摩擦单元的试验研究，并提出了相关设计方法。吕西林等[10]提出了一种螺栓装配式梁柱节点，通过振动台试验验证了节点力学性能，并提出了构造设计建议。Hong[11]提出了端板螺栓装配式梁柱节点，开展了试验研究，并提出了构件和结构层次的设计方法。研究表明：干式装配梁-柱节点的研发应面向以下需求：1)构造形式简洁易施工，充分体现干式装配的特点；2)力学性能可靠易调控，且适应于结构体系的性能需求。

基于上述需求，本研究提出了一种转动摩擦型干式装配梁-柱节点(rotational friction dissipative joint,RFDJ)，具有刚度、屈服弯矩易调控和变形、耗能能力强的特点。为了研究RFDJ 对于装配式框架结构抗震性能的影响并验证其可行性，以含RFDJ 和灌浆套筒柱脚节点的新型装配式框架结构体系(novel precast concrete frame, NPCF)作为研究对象，综合考虑楼层数量和结构关键设计参数，设计了2 个传统现浇框架结构(reinforced concrete frame,RCF)分析案例和120 个NPCF 结构分析案例，开展了多遇和罕遇地震作用下的结构非线性时程分析，分析了关键设计参数对NPCF 抗震性能的影响，研究了NPCF 结构的地震响应控制机制。

1 转动摩擦型干式梁-柱节点及具有其的装配式框架结构

1.1 转动摩擦型干式梁-柱节点

本研究提出的转动摩擦型干式装配梁-柱节点(rotational friction dissipative joint, RFDJ)构造如图1所示。柱端耳板、梁端耳板、环形摩擦片和预紧螺栓构成了可转动耗能的摩擦铰。梁端和柱端预埋件使得预制混凝土梁柱与摩擦铰通过螺栓连接，以实现RFDJ 的干式连接。

图1 RFDJ 构造Fig. 1 Configuration of RFDJ

相比于传统等同现浇型装配式梁-柱节点，RFDJ 具有以下特点：

1)刚度、屈服弯矩易调控。

RFDJ 的转角-弯矩关系是由摩擦铰决定的，相关研究[12-13]中转动型摩擦阻尼器与摩擦铰的基本原理一致，试验[12]和数值模拟[13]研究均表明转动型摩擦阻尼器呈现典型的理想弹塑性的滞回模型，与支撑型[14]摩擦阻尼器相同。因此，RFDJ 的转角-弯矩关系呈现为如图2 所示的典型理想弹塑性滞回模型。摩擦铰发生转动摩擦前，RFDJ 保持弹性；摩擦铰起滑后，RFDJ 屈服，节点承载力恒定。因此，RFDJ 的转角-弯矩关系可由初始刚度ke和起滑弯矩Ms两个参数描述。

图2 RFDJ 理论转角-弯矩关系Fig. 2 Theoretical moment-rotation relationship of RFDJ

摩擦铰起滑前的RFDJ 可等效为弹性钢梁，ke可通过调整预埋件和连接件的截面尺寸调控。为了兼容我国现行规范中现浇混凝土框架结构的设计方法，建议ke的取值与同梁柱截面的现浇梁-柱节点的弹性转动刚度相等。值得注意的是，在选取预埋件和连接件的截面尺寸时，还应充分考虑RFDJ 节点梁端的抗剪、抗扭刚度和强度。

参数Ms可根据库仑-摩擦定律，在极坐标内积分计算：

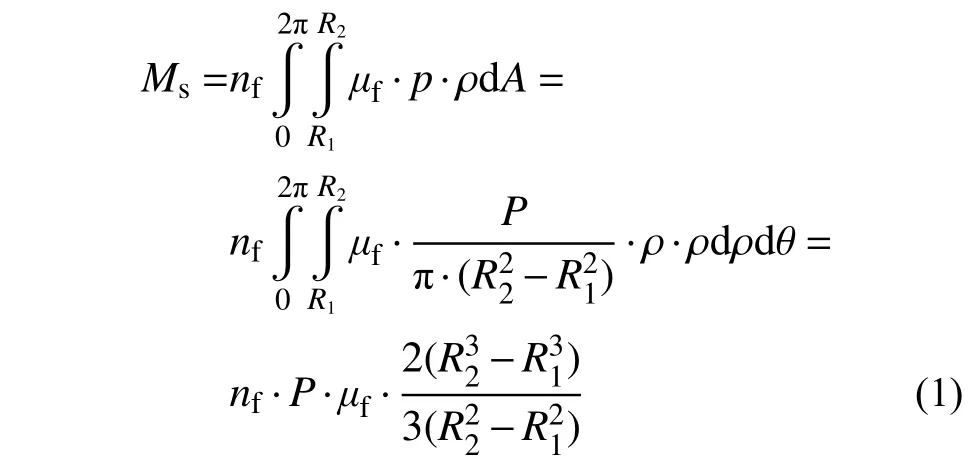
式中：nf为摩擦面的数量；µf为摩擦片与耳板表面间的摩擦系数；R1和R2分别为环形摩擦片的内径和外径；P为预紧螺栓上施加的总预紧力。国巍等[13]推导的转动型摩擦阻尼器的理论计算公式与式(1)相同，这是因为RFDJ 中摩擦铰的耗能机理与该阻尼器一致，精细数值模拟结果表明该公式具有可靠性和较高的准确性。基于上述原理，通过调整预紧力螺栓的预紧力，可实现RFDJ 的屈服弯矩(即起滑弯矩Ms)的调控。

由以上分析可知，传统等同现浇型装配式梁-柱节点的刚度和屈服弯矩是相互耦合的，难以分别调控。而RFDJ 的刚度和屈服弯矩解耦，具有易调控的特点。因此，相比于传统等同现浇型梁-柱节点，RFDJ 更易于实现节点力学性能与需求的匹配，可形成明确简便的设计方法。同时，RFDJ 的变形模式与传统现浇节点的理想变形模式相同，变形集中于梁端，符合“强柱弱梁”的设计理念。

2)变形、耗能能力强。

传统等同现浇型装配式梁-柱节点的变形能力是有限的，随着位移的增加，承载力逐渐依次上升到屈服点和峰值点，随后进入下降段。通常认为混凝土构件在承载力下降至峰值的85%时失效[15]。然而对于RFDJ，达到屈服弯矩后将保持恒定，因此理论上，RFDJ 的变形能力并非受节点的承载力控制，在几何尺寸设计合理的前提下具有显著优于传统等同现浇型节点的变形能力。

同时，由图2 可见，RFDJ 呈现理想弹塑性模型的滞回曲线，为饱满的平行四边形。而传统等同现浇型梁-柱节点的滞回曲线通常呈现为具有明显捏拢特征的梭形[16]。因此在相同变形水准下，RFDJ 具有更好的耗能能力。

1.2 含RFDJ 的新型装配式框架

上述分析指出了RFDJ 在构件层次抗震性能的优越性。为了研究RFDJ 对于装配式框架结构抗震性能的影响并验证其可行性，本研究对含RFDJ 的装配式混凝土框架结构开展抗震性能研究。值得注意的是，除梁-柱节点外，柱脚节点对装配式框架抗震性能同样具有重要影响，本研究在此选取研究和工程中具有代表性且广泛应用的灌浆套筒柱脚节点，该类节点可实现等同现浇的力学性能[17]。综上，本研究的研究对象即为如图3 所示的含RFDJ 和灌浆套筒柱脚节点的新型装配式框架结构体系(novel precast concrete frame, NPCF)。

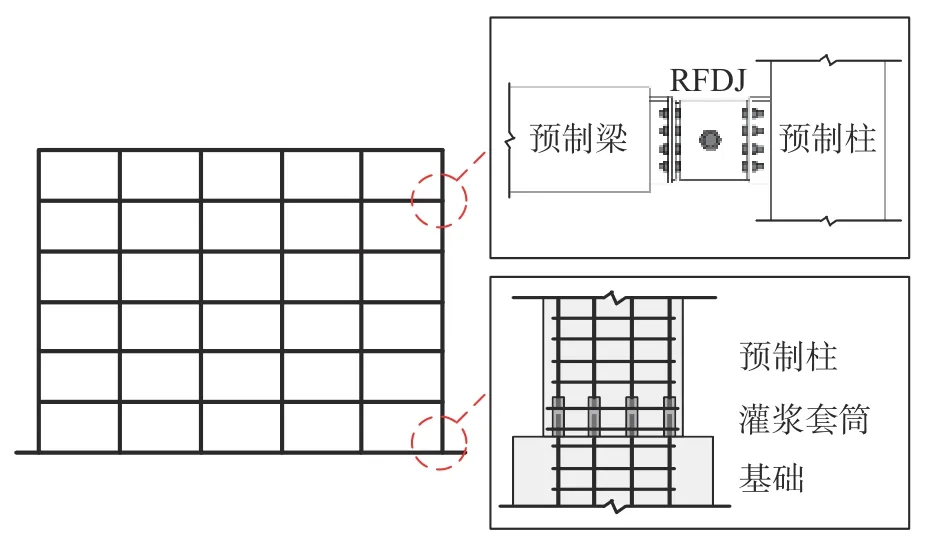
图3 含RFDJ 和灌浆套筒柱脚的新型装配式框架结构体系Fig. 3 Novel precast concrete frame with RFDJs and grouted sleeve column-base joints

1.3 新型装配式框架的关键设计参数识别

研究表明：灌浆套筒柱脚可实现与现浇柱脚相同的抗震性能[17]。因此NPCF 与现浇框架结构可能存在的抗震性能差异是由RFDJ 引起的。由前文分析可知，在节点构件层次，初始刚度ke和起滑弯矩Ms决定RFDJ 的转角-弯矩关系，是影响RFDJ力学性能的关键设计参数。在整体结构层次，各个RFDJ 的转角-弯矩关系对结构抗震性能存在重要影响。其中，ke的取值与同梁柱截面的现浇梁-柱节点的弹性转动刚度相等，因此，NPCF 结构中各RFDJ 的Ms取值对结构抗震性能具有主要影响。

本研究采用总起滑弯矩比ρ 和起滑弯矩分布系数αi两个无量纲参数表征各RFDJ 的Ms的值。值得注意的是，当同一楼层中各RFDJ 具有相同的Ms取值时，可为NPCF 的设计和建造提供便利。因此，本文假定同一楼层中各RFDJ 具有相同的Ms取值，则可用ρ 用于描述结构中所有RFDJ的Ms之和的相对值，按式(2)计算：

式中：nb为框架跨数；Ms,i为第i层中RFDJ 的Ms；OTMbase为结构布置和构件截面尺寸相同的现浇框架结构弹性小震反应谱分析得到的基底倾覆弯矩。

αi用于描述各楼层Ms的相对值分布，即：

根据式(2)和式(3)，结构中楼层i中RFDJ 的起滑弯矩为：

由式(4)可见ρ 和αi(即Ms分布模式)共同决定了结构中各RFDJ 的Ms取值，因此，ρ 和Ms分布模式对NPCF 抗震性能存在影响，有必要通过参数分析研究确定其是否为决定NPCF 抗震性能的关键设计参数。

2 案例设置、分析模型与地震动选取

2.1 分析案例设置

为研究RFDJ 对于装配式框架结构抗震性能的影响并验证其可行性，探究关键设计参数对NPCF抗震性能的影响，并揭示NPCF 结构地震响应控制机制，本研究以不同楼层数量的2 个现浇框架结构作为基准，考虑不同层数、Ms分布模式和ρ 的影响，形成了120 个NPCF 结构分析案例，具体而言：

设计了层数分别为6 层和9 层的现浇框架结构作为基准结构。其抗震设防烈度为8 度(0.2g)，场地类型为II 类，设计地震分组为第二组。结构布置如图4 所示，6 层和9 层框架的梁截面分别为300 mm×500 mm 和350 mm×550 mm，柱截面分别为450 mm×450 mm 和550 mm×550 mm，两者分别命名为RCF6 和RCF9，建立结构模型并开展相关分析计算。RCF6 和RCF9 的一阶周期分别为1.073 s 和1.271 s，小震弹性反应谱分析层间位移角分别为1/625 和1/743，满足规范[18]限值1/550的要求。

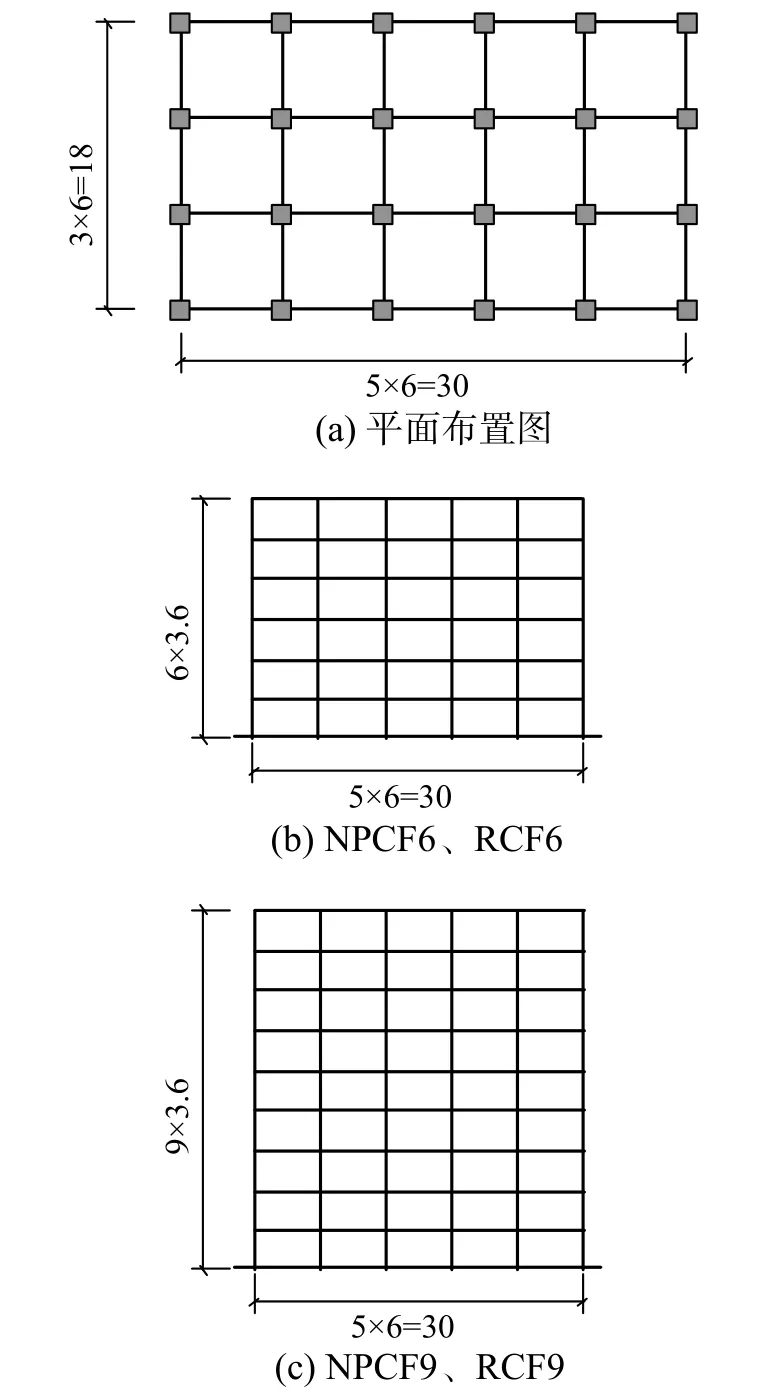
图4 分析案例结构布置图 /mFig. 4 Plan view of study cases

为对比NPCF 与现浇框架结构抗震性能的差异，基于基准现浇结构RCF6 和RCF9，选取相同的结构布置和构件截面尺寸，并将梁柱节点替换为RFDJ，形成了新型装配式框架体系案例结构NPCF6 和NPCF9。其 中RFDJ 的ke与RCF 中 对应梁-柱节点的弹性转动刚度相等，因此NPCF 与对应RCF 的一阶周期一致。

为探究设计参数对NPCF 抗震性能的影响，通过调整ρ 的取值和Ms分布模式形成了一系列NPCF 设计案例。ρ 的取值为20 个，介于0～26 之间。本研究在此借鉴Lu 等[19]提出的结构性能调控技术，拟通过设置不同楼层间RFDJ 的耗能能力极差，引导更为合理的控制机理和控制效果，为此考虑了如图5 所示的3 种Ms分布模式，分别为：1)均匀分布，各楼层RFDJ 的Ms相同；2)均匀累积分布，Ms随楼层增大而减小，且相邻楼层Ms差值相等；3)一阶振型位移角分布，即各楼层Ms按结构一阶振型层间位移角的比例关系分配。其中，前两种分布模式与结构特性无关，一阶振型位移角分布模式与结构动力特性相关。

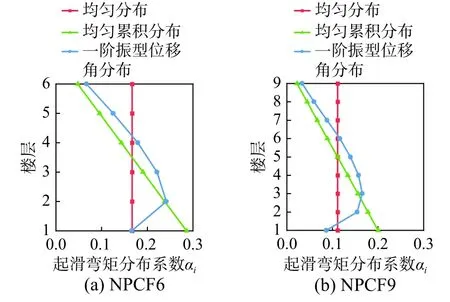
图5 NPCF 设计案例考虑的3 种Ms 分布模式αi 取值Fig. 5 Values of αi of three Ms distribution patterns of NPCF study cases

综上所述，在不同层数的两个RCF 基准结构的基础上，考虑2 种楼层数、20 个ρ 的取值和3 种Ms分布模式，共设计了120 个NPCF 分析案例，用于开展非线性时程分析。

2.2 弹塑性有限元模型

采用OpenSees[20]建立了2.1 节中RCF 和NPCF结构的弹塑性有限元分析模型。陆新征等[16,19,21-22]提出了适用于混凝土框架结构的精细数值模拟方法，该方法精度好、效率高，能够完整揭示结构的损伤演化机理和控制机理，在此本研究采用上述方法建立结构有限元模型。混凝土梁柱均采用基于位移的纤维梁柱单元模拟，其中钢筋纤维采用Steel02 材料，混凝土纤维采用Concrete01 材料。约束区和保护层混凝土本构关键点参数均采用Kent-Scott-Park 模型计算[23]。

本研究基于OpenSees 提出了适用于RFDJ 的宏观数值模拟方法，如图6 所示。连接件和预埋件在地震作用下保持弹性，因此，采用弹性梁单元模拟。摩擦铰采用零长度转动弹簧单元模拟，弹簧力学属性采用理想弹塑性单轴材料表征，初始刚度为极大值，屈服荷载为Ms。

图6 RFDJ 宏观数值模型Fig. 6 Macro numerical model of RFDJ

2.3 地震动选取

基于抗震规范相关要求和设计反应谱[18]，采用PEER NGA West 2 数据库[24]选取了13 条天然地震动时程记录用于弹塑性时程分析。设计反应谱与选取地震动平均反应谱吻合良好，如图7 所示。根据规范要求，开展多遇和罕遇地震作用下弹塑性时程分析时，地震动的峰值加速度分别调幅至70 cm/s2和400 cm/s2。

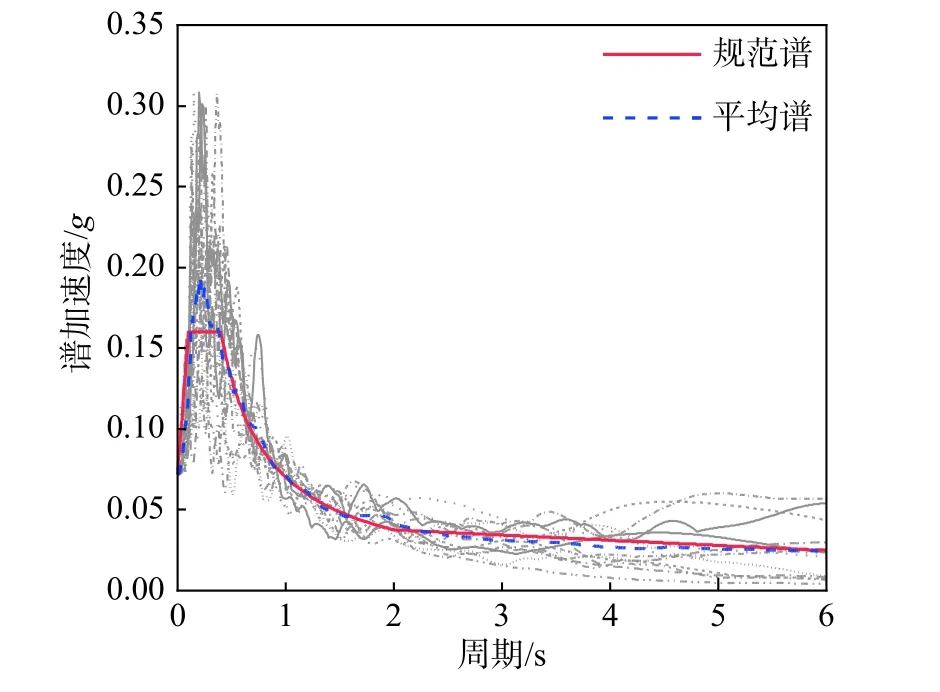
图7 选取地震动反应谱与规范反应谱对比Fig. 7 Comparison between mean spectra of selected ground motions and design spectrum of code

3 结构地震响应分析

为了研究RFDJ 对于装配式框架结构抗震性能的影响并验证其可行性，探究关键设计参数对NPCF 抗震性能的影响，并揭示NPCF 结构地震响应控制机制，采用上述13 条地震动开展了多遇地震和罕遇地震作用下RCF 和NPCF 案例结构的弹塑性时程分析，主要地震响应结果分析如下。

3.1 最大层间位移角

最大层间位移角(θmax)是广泛用于各国规范和相关研究的结构性能评价指标[21,25-28]。本文通过计算NPCF 和RCF 最大层间位移角(和)的相对差值Rθ定量对比NPCF 和RCF 的抗震性能，即：

具有不同Ms分布模式和ρ 取值的NPCF6 和NPCF9 案例结构在多遇地震和罕遇地震作用下的Rθ和θmax分别如图8 和图9 所示。由图可见：

图8 PCF6 分析案例最大层间位移角Fig. 8 Maximum inter-story drift ratio of NPCF6

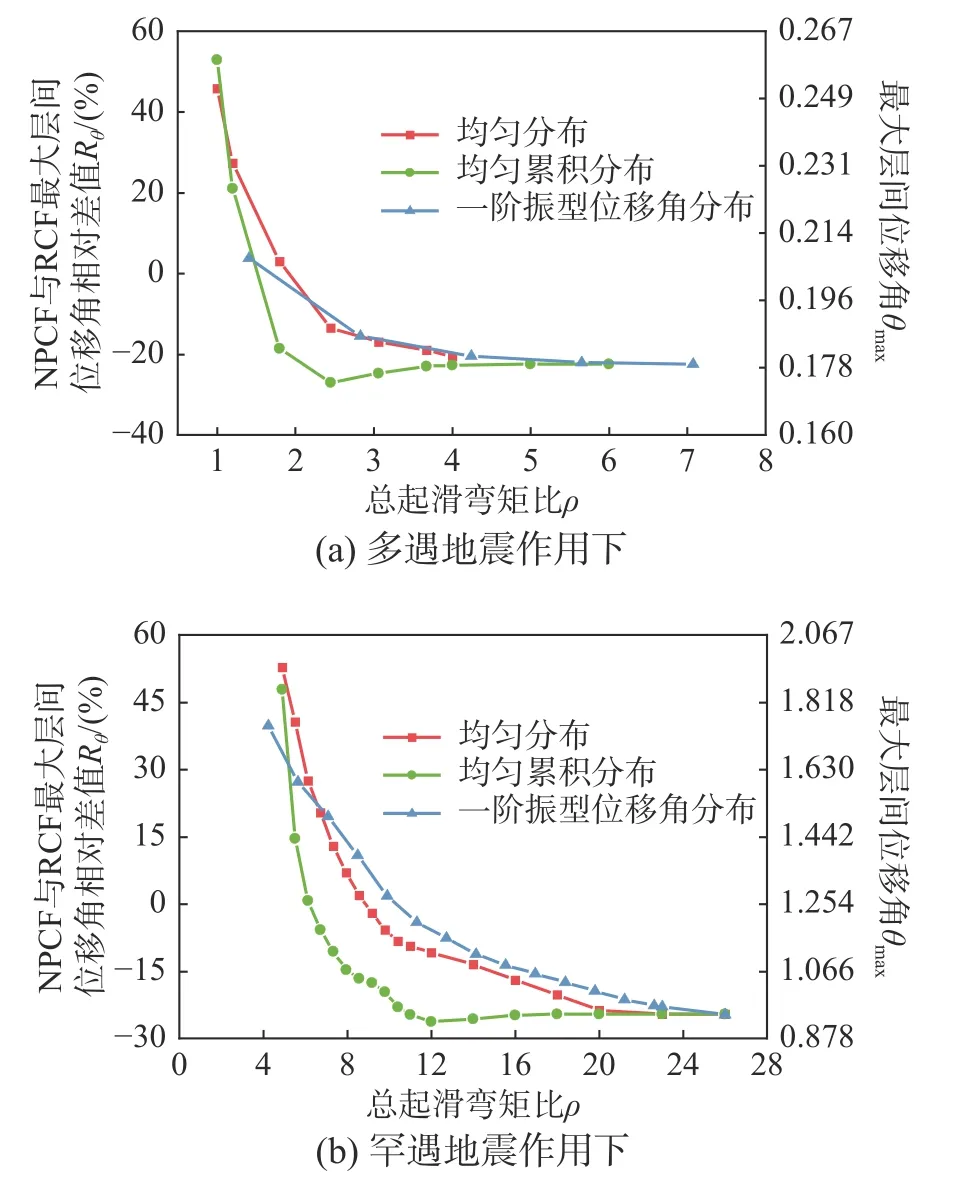
图9 NPCF9 分析案例最大层间位移角Fig. 9 Maximum inter-story drift ratio of NPCF9

1) RFDJ 具备用于装配式框架结构的可行性。当Ms分布模式和ρ 的取值合理时，NPCF 可满足抗震规范对框架结构在多遇地震下1/550 和罕遇地震作用下1/50 的层间位移角限制要求，并且可实现小于0 的Rθ。因此，NPCF 可实现等同甚至优于RCF 的抗震性能。

2) ρ 的取值对Rθ具有显著影响。总体上Rθ随ρ 的增加而降低，当ρ 达到阈值 ρ*时，Rθ收敛于。这是由于 ρ*对应于较高的Ms取值，此时结构中摩擦铰均不发生摩擦转动，因此在 ρ*基础上进一步提高ρ 的值不会对NPCF 的结构响应产生变化。值得注意的是，各案例结构的均小于0。NPCF6 在多遇和罕遇地震下分别为-2.67%和-17.12%，NPCF9 在多遇和罕遇地震下分别为-22.44%和-24.54%。这是因为摩擦铰不发生转动的NPCF 结构等同于梁端为弹性钢梁的混凝土框架结构，结构的屈服后刚度高于现浇混凝土框架结构。

3)Ms分布模式对Rθ-ρ 曲线的形状存在影响。对于采用均匀分布和一阶振型位移角分布的案例结构，除多遇地震作用下的NPCF6 外，Rθ-ρ 曲线均为单调递减曲线，Rθ随ρ 的增加而降低，并收敛于。然而，对于采用均匀累计分布的案例结构，Rθ-ρ 曲线均为存在极小值的非单调曲线，具体而言，Rθ首先随ρ 的增加而显著降低，在达到最小值后，Rθ随ρ 的增加小幅增长，最终收敛于。

由图8 和图9 可知，当罕遇地震作用下θmax满足规范限制要求1/50 时，ρ 值基本接近多遇地震作用下的 ρ*。则在满足规范变形限值要求的前提下，ρ 值主要影响罕遇地震作用下的结构响应。因此，本研究以罕遇地震作用下的Rθ和θmax作为衡量NPCF 抗震性能的标准。对于每种Ms分布模式，选定罕遇地震作用下Rθ达到最低值Rθ,min的结构作为最优案例结构。

表1 中列出了采用不同Ms分布模式的最优案例结构在罕遇地震作用下的Rθ,min及对应的ρ 值。可见，采用均匀累积分布时，Rθ,min最小，且对应的ρ 值同样最小。进而RFDJ 节点的Ms需求较小，降低了摩擦铰中预紧螺栓的预紧力需求，有利于RFDJ 节点的深化设计和施工。因此，均匀累积分布具有更高的层间位移角控制效率。

表1 最优案例结构罕遇地震作用下的Rθ, min 及对应的ρTable 1 Values of Rθ, min and ρ of optimal study cases under MCE

3.2 层间位移角分布

罕遇地震作用下最优NPCF 案例结构和对应的RCF 案例结构在多遇和罕遇地震作用下的层间位移角分布如图10 所示。

多遇地震作用下，采用不同Ms分布模式的NPCF 具有相同的层间位移角分布，说明各案例结构摩擦铰均未发生转动摩擦，结构地震响应一致，与3.1 节相关分析结论相同。罕遇地震作用下，采用均匀累计分布的NPCF 具有最小的层间位移角，而采用均匀分布和一阶振型位移角分布的NPCF层间位移角分布基本一致。

层间位移角集中系数(drift concentration factor,DCF)被广泛用于量化表征框架结构层间位移角分布的集中程度[25]，按下式计算：

式中：θmax为最大层间位移角；θroof为结构顶点位移角。DCF=1 表示结构层间位移角均匀分布，DCF越大，则层间位移角分布不均匀程度越高。

罕遇地震作用下，最优案例结构的DCF 如表2 所示，RCF6 和RCF9 的DCF 分 别 为1.39 和1.62。可见，采用各Ms分布模式的NPCF 的DCF均小于RCF 的DCF，结合图10 可知，相比于RCF，NPCF 结构的层间位移角分布更均匀。

图10 最优案例结构层间位移角分布Fig. 10 Distribution of story drift ratio (θ)of optimal study cases

表2 最优案例结构罕遇地震作用下的DCFTable 2 DCF of study cases under MCE

同时值得注意的是，采用均匀累积分布的NPCF6 和NPCF9 具有最小的DCF，分别为1.24 和1.26，而采用另外两种Ms分布模式时DCF 相近。因此，采用均匀累积分布时，层间位移角分布更均匀。

3.3 RFDJ 工作状态

上述分析表明：RFDJ 的工作状态对NPCF 结构的地震响应和抗震性能具有关键影响。为了深入揭示NPCF 结构的地震响应控制机理，有必要对案例结构中RFDJ 的工作状态进行具体分析。本研究以RFDJ 弯矩利用率β 描述RFDJ 的工作状态，即β=Mj/Ms，其中Mj为摩擦铰在地震作用下承担的弯矩。β＜1 表示RFDJ 处于起滑前锁定状态，β=1 表示处于转动摩擦工作状态。

罕遇地震作用下最优案例结构各楼层的β 如图11 所示。对于采用均匀累计分布的NPCF，2 层及以上楼层的β 均为1。然而对于采用另外两种Ms分布模式的NPCF，仅有采用一阶阵型位移角分布的NPCF9 的结构底层β=1，其它案例结构β 均小于1。

图11 最优案例结构罕遇地震作用下RFDJ 弯矩利用率Fig. 11 RFDJ moment usage ratio of optimal study cases under MCE

由上述现象可知，对于采用均匀累积分布的最优案例结构，NPCF 中绝大多数RFDJ 处于摩擦转动工作状态，RFDJ 的耗能能力得到了充分的利用。而采用另外两种Ms分布的最优案例结构，NPCF中绝大多数RFDJ 仍处于起滑前锁定状态，RFDJ无法耗散地震能量。

因此，3.1 节中Ms分布模式对Rθ-ρ 曲线的形状存在影响的实质是Ms分布模式对NPCF 结构地震响应控制机制具有显著影响。具体而言，采用均匀累积分布时，结构耗能能力和需求得到了良好的匹配，NPCF 的结构响应控制是通过RFDJ 的耗能特性以及提高节点屈服后承载力和割线刚度实现的。然而采用其余两种Ms分布模式时，无法匹配NPCF 结构的耗能需求分布，NPCF 的结构响应控制是通过提高节点屈服后承载力和割线刚度实现的。因此，采用均匀累积分布时，以最小的ρ 值即可实现最好的层间位移角控制效果，具有更高的层间位移角控制效率。

4 结论

本研究提出了一种转动摩擦型干式装配梁-柱节点(rotational friction dissipative joint, RFDJ)，具有力学性能可调控和变形、耗能能力强的特点。为了研究RFDJ 对于装配式框架结构抗震性能的影响并验证其可行性，本研究以含RFDJ 和灌浆套筒柱脚节点的新型装配式框架结构体系(novel precast concrete frame, NPCF)作为研究对象，综合考虑2 种楼层数量、20 个总起滑弯矩比(ρ)取值和3 种起滑弯矩(Ms)分布模式，设计了2 个传统现浇框架结构(reinforced concrete frame, RCF)分析案例和120个NPCF 结构分析案例，开展了多遇和罕遇地震作用下的结构非线性时程分析，识别并探究了关键设计参数对NPCF 抗震性能的影响，揭示了NPCF结构地震响应控制机制，得出以下主要结论：

(1) RFDJ 具备用于装配式框架结构的可行性。经合理设计，NPCF 可满足抗震规范对框架结构层间位移角限值的要求，可实现比传统RCF 更小的层间位移角，并实现等同或优于RCF 的抗震性能。

(2) ρ 和Ms分布模式是共同决定NPCF 抗震性能的关键设计参数。

(3) ρ 的取值对NPCF 结构的地震响应水准具有显著影响，总体上结构地震响应随着ρ 的增大而降低，并最终收敛于稳定值。

(4)Ms分布模式对NPCF 结构的地震响应控制机制具有显著影响。采用均匀累积分布时，以最小的ρ 值即可实现最好的层间位移角控制效果，有利于节点深化设计和施工。同时，采用均匀累积分布时，层间位移角分布更均匀。