磁浮车辆-桥梁耦合系统随机振动分析的时域显式方法研究
陆周瑞,陈 冉,苏 成,2
(1. 华南理工大学土木与交通学院,广州 510640;2. 华南理工大学亚热带建筑科学国家重点实验室,广州 510640)
磁浮列车以其运行速度高、乘坐舒适安全、线路适应能力强、运营维护成本低等优势,成为当前颇具竞争力的地面轨道交通运输工具[1-4]。目前,国内外已建成多条磁浮列车商业线路,我国600 km/h 高速磁浮试验样车也已进入试跑阶段。当磁浮列车高速通过高架桥梁时,轨道不平顺是诱发磁浮车辆和桥梁耦合振动的重要因素,直接影响行车舒适性和稳定性[5-6]。经典的车桥耦合动力学理论主要聚焦于确定性振动分析方面,考虑输入系统的激励是确定性函数(如某一轨道不平顺样本),研究单一给定激励作用下车桥系统的动力响应。事实上,轨道不平顺具有本质的随机性,而车桥耦合系统本身是一个时变体系,在轨道随机不平顺作用下的车桥耦合振动是典型的非平稳随机振动问题,需要在非平稳随机振动理论框架下进行研究。考虑轨道不平顺等激励源的随机特性,开展磁浮车辆-桥梁耦合系统(以下简称磁浮车桥耦合系统)随机振动分析方法研究具有重要的理论价值和现实意义。
已有的车桥耦合系统随机振动分析方法可以划分为统计型方法[5,7-9]和非统计型方法[10-19]。统计型方法即传统的随机模拟法(也称Monte Carlo 模拟法),该法通过计算车桥耦合系统在大量随机生成激励样本下的时域响应,统计得到车桥动力响应的随机特征,如文献[5]采用轨道不平顺谱生成样本,模拟计算了TR06 磁浮车桥耦合系统时域上的随机响应,通过时频变换给出系统随机响应的功率谱。统计型方法本质上是针对样本的确定性分析方法,其优点是原理简单和适用性广,但计算效率严重依赖于所需样本量和单样本时程分析效率,难以满足大型复杂磁浮车桥耦合系统随机振动计算的需求。非统计型方法指基于随机振动理论的分析方法,主要有谱演化法(包括功率谱法[10-11]和虚拟激励法[12-15])、矩演化法[16]和概率密度演化法[17-19]等。其中,虚拟激励法已被应用于磁浮车辆随机振动问题,如文献[12]基于虚拟激励原理,提出磁浮车辆系统受多点异相位平稳随机激励的响应功率谱计算方法,但未考虑磁浮车辆与桥梁的耦合振动问题。总体而言,对于一般的车桥耦合系统随机振动问题,已开展了大量研究,但针对磁浮车桥耦合系统随机振动问题,相关研究尚不多见。
时域显式法(explicit time-domain method)是近年来发展起来的一类针对大规模系统的高效非平稳随机振动分析方法[20-23]。该法通过构建系统动力响应的时域显式表达式,实现系统物理演化机制与概率演化机制的相对分离,在获取响应统计矩的过程中,无须反复求解系统运动方程,同时可以任意选取所关注的自由度进行降维计算。最近,时域显式法已成功应用于线弹性接触[24]和非线性赫兹接触[25]的轮轨车桥耦合系统随机振动分析,展现了良好的计算精度和效率。
本文在文献[24 - 25]的基础上,进一步发展了考虑轨道随机不平顺作用的磁浮车桥耦合系统随机振动分析时域显式法。分别从车辆系统和桥梁系统的运动方程出发,结合车轨间的电磁力方程和几何相容条件,构建表征车桥相互作用的电磁力关于轨道不平顺的时域显式表达式,并进一步得到磁浮车桥耦合系统关键响应关于轨道不平顺的时域显式表达式。在此基础上,利用统计矩运算法则或随机模拟法,高效计算磁浮车桥耦合系统关键响应的演变统计矩。数值算例表明,本文所提方法具有理想的计算精度与效率。
1 磁浮车桥耦合系统的基本方程
1.1 计算模型
为了阐述时域显式法的列式过程,考虑二自由度常导电磁悬浮型车辆以匀速V通过简支梁桥的计算模型,如图1 所示。车辆系统由车体、车体悬架和电磁铁组成,采用多刚体建模,m1和m2分别为车体和电磁铁的质量,ks和cs分别为车体悬架的刚度和阻尼。桥梁系统采用平面梁单元建模,L为桥梁跨度, ρAb和EIb分别为桥梁的线密度和抗弯刚度。假定磁浮车辆通过桥梁前桥面在自重作用下保持水平,并假定轨道与桥面之间不存在相对位移,w(x)为轨道不平顺随机场,以向下为正,其中x=Vt。
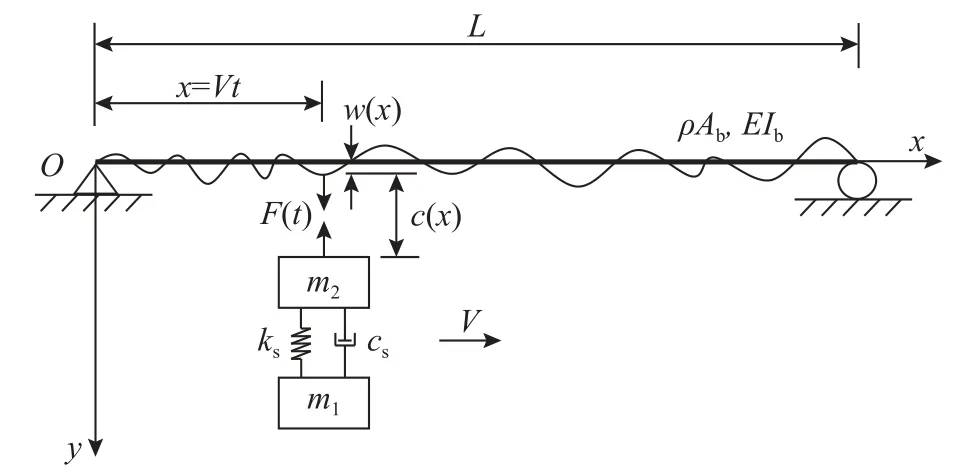
图1 二自由度磁浮车辆-桥梁耦合系统力学模型Fig. 1 Mechanical model for a 2-DOF maglev vehicle-bridge coupled system
1.2 磁浮车辆系统运动方程
车辆系统的运动方程可以列为:
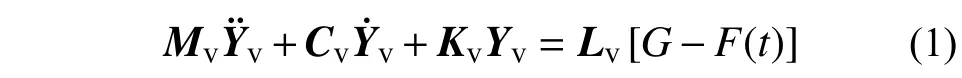
式中:下标v 表示车辆(vehicle);Mv、Cv和Kv分别为车辆系统的质量矩阵、阻尼矩阵和刚度矩阵;Yv、和分别为车辆系统的位移向量、速度向量和加速度向量,方向以向下为正,并取车辆系统在岸上的静悬浮位置为原点;G为车辆系统的重力;F(t) 为 电磁吸引力,如图1 所示;Lv为作用于车辆电磁铁上荷载 [G-F(t)]的定位向量。
1.3 桥梁系统运动方程
桥梁系统的运动方程可以列为:
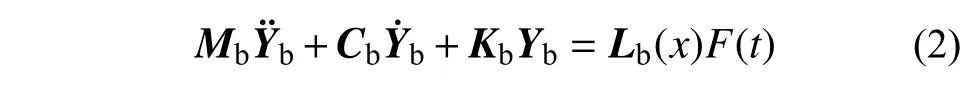
式中:下标b 表示桥梁(bridge);Mb、Cb和Kb分别为桥梁系统的质量矩阵、阻尼矩阵和刚度矩阵;Yb、和分别为桥梁系统的位移向量、速度向量和加速度向量,方向以向下为正,并取车辆通过桥梁前的桥梁系统静平衡位置为原点;Lb(x) 为 车辆位置x处 电磁力F(t)的定位向量。
1.4 电磁力方程
与轮轨直接接触方式不同,磁浮车辆借助电磁铁和轨道之间的电磁吸引力克服重力作用,实现悬浮。任意瞬时的电磁力可以表示为:
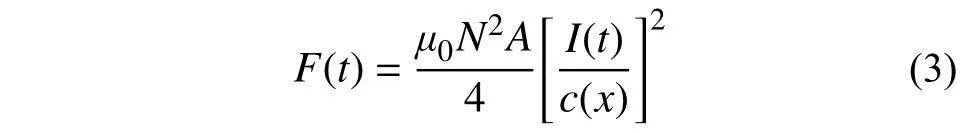
式中:μ0为空气磁导率;N为电磁铁线圈匝数;A为有效磁极面积;I(t) 为 电磁铁电流;c(x)为悬浮间隙,x=Vt,如图1 所示。
式(3)说明了电磁力是关于电流和悬浮间隙的非线性函数。假定车辆静悬浮时,电流和悬浮间隙分别为I0和c0,此时电磁力F0=G。考虑到车辆运行时控制电流和悬浮间隙的变化较小[5],在I0和c0处对电磁力进行一阶泰勒展开,可将电磁力表达为如下线性函数:
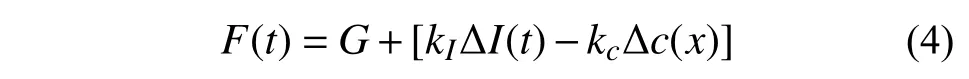
式中: ΔI(t) 和 Δc(x)分别为电流变化量和悬浮间隙变 化 量;kI和kc分 别 为 ΔI(t) 和 Δc(x)的 比 例系数,其表达式分别为:
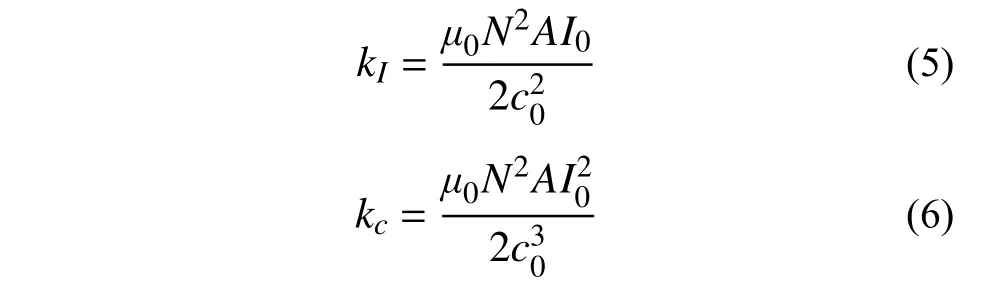
1.5 电流控制律和车轨几何相容条件
电磁力是有源主动控制力,通常可以将悬浮间隙变化量等信号输入悬浮控制器,实现电磁力的动态调整,进而控制悬浮间隙变化量,保持车辆的悬浮稳定性。选取悬浮间隙变化量 Δc(x)、车辆电磁铁竖向速度(t) 和 竖向加速度(t)为状态反馈量,则电流控制律可以写为[8]:
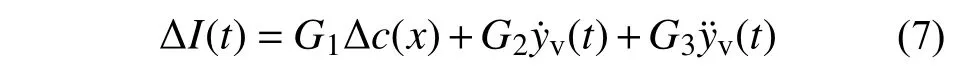
式中,G1、G2和G3分别为 Δc(x) 、(t) 和(t)的反馈系数。
根据车辆和桥梁之间的几何相容条件,由图1可得悬浮间隙变化量 Δc(x)的表达式为:
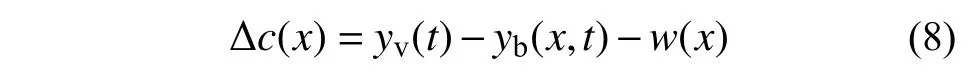
式中:yv(t) 为 车辆电磁铁竖向位移;yb(x,t)为电磁力作用点处桥梁竖向位移。
将式(7)和式(8)代入式(4),整理后可得:
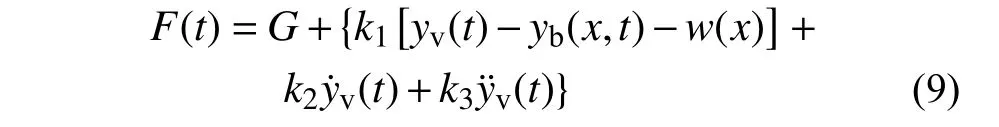
式中:
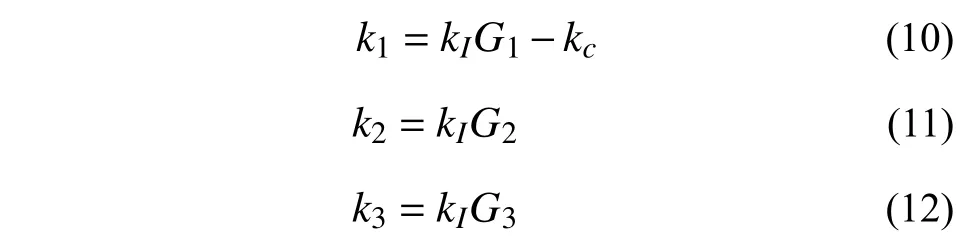
由以上推导可见,电磁力式(9)综合考虑了线性化电磁力方程式(4)、电流控制律式(7)和几何相容条件式(8),揭示了车桥运动状态及轨道不平顺对电磁力的影响机制。
2 系统响应的时域显式表达式
2.1 系统响应关于电磁力的显式表达
采用任意一种数值积分方法,如Newmark-β法,分别求解运动方程式(1)和式(2),导出车辆和桥梁响应关于各离散时刻电磁力F(ti)的显式表达式:

2.2 电磁力关于轨道不平顺的显式表达
考虑全部时刻的电磁力,由式(9)可得:
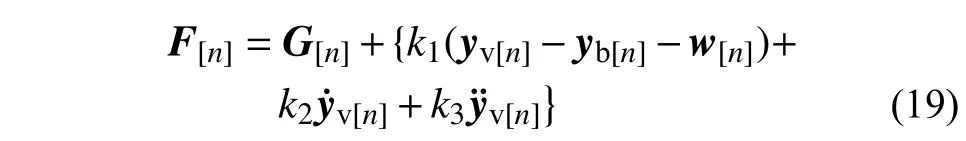
式中,w[n]=[w(x1)w(x2) ···w(xn)]T。
将式(15)~式(18)代入式(19),整理后可得:
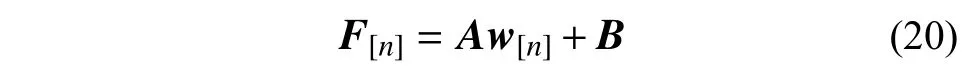
式中:
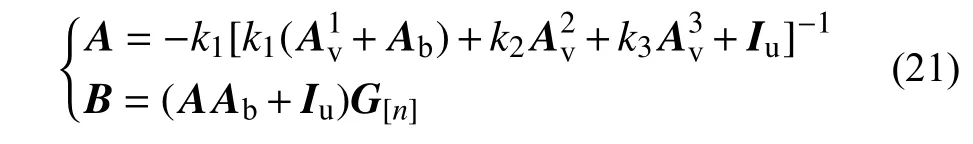
式中,Iu为n阶单位矩阵。
式(20)即为电磁力向量F[n]关于轨道不平顺向量w[n]的显式表达式,该式从本质上反映了磁浮车桥耦合系统的物理演化过程。
2.3 系统关键响应关于轨道不平顺的显式表达
式(13)和式(14)分别给出了电磁力作用下磁浮车辆系统和桥梁系统的响应表达式,而式(20)则给出了电磁力关于轨道不平顺的表达式。因此,可以进一步推导车辆系统和桥梁系统关键响应关于轨道不平顺的显式表达式。假定rv(t)和rb(t)分别为磁浮车辆系统和桥梁系统的某一关键响应。同样地,由式(13)和式(14)可以得到全部时刻rv(ti)和rb(ti)(i=1,2,···,n)分别为:

将式(20)分别代入式(22)和式(23)中,整理后可得磁浮车辆系统和桥梁系统关键响应关于轨道不平顺的显式表达式:
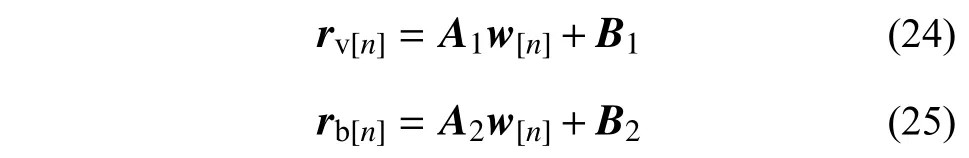
式中:
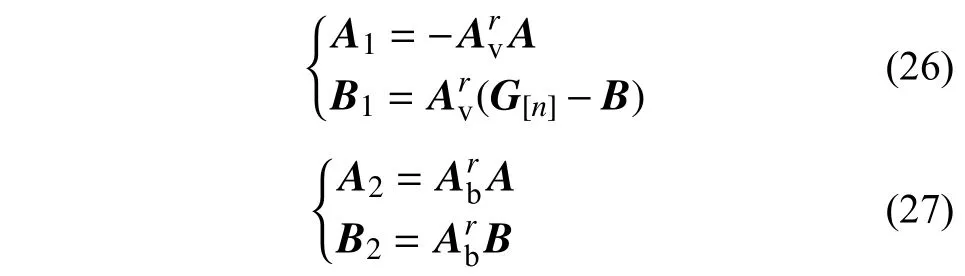
2.4 电流变化量及悬浮间隙变化量关于轨道不平顺的显式表达
除了车辆系统和桥梁系统的关键响应外,与磁浮车辆行驶稳定性密切相关的控制电流变化量和悬浮间隙变化量也应重点关注。由式(7)和式(8)可 以 得 到 全 部 时 刻 ΔI(ti) 和Δc(ti)(i=1,2,···,n)分别为:
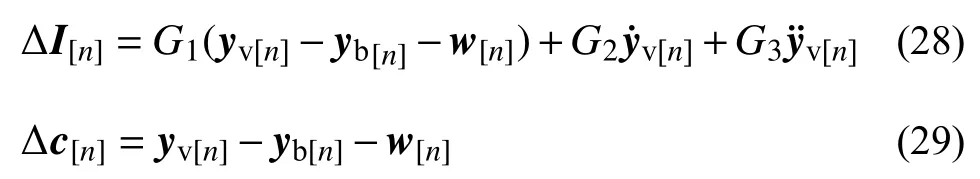
式 中: ΔI[n]=[ΔI(t1)ΔI(t2) ··· ΔI(tn)]T,Δc[n]=[Δc(t1) Δc(t2) ··· Δc(tn)]T。
将式(20)代入式(15)~式(18),然后再分别代入式(28)和式(29),整理后可得电流变化量和悬浮间隙变化量关于轨道不平顺的显式表达式:
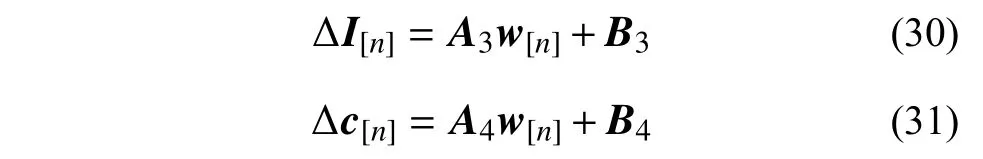
式中:
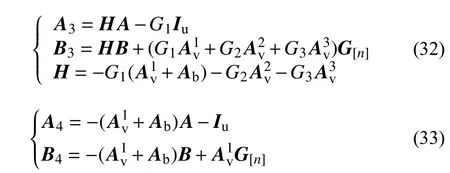
至此,已经获得磁浮车桥耦合系统关键响应、控制电流变化量以及悬浮间隙变化量关于轨道不平顺的显式表达,分别如式(24)、式(25)、式(30)和式(31)所示。当给定轨道不平顺随机场的功率谱密度函数或相关函数后,即可利用上述式子开展磁浮车桥耦合系统随机振动分析。
3 磁浮车桥耦合系统随机振动分析
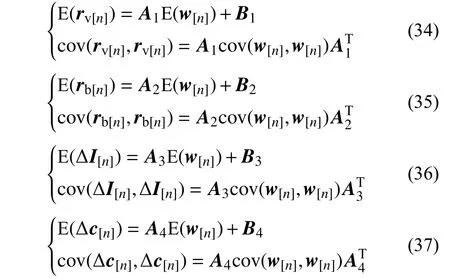
3.1 时域显式直接法
式中, E(w[n]) 和 cov(w[n],w[n])分别表示轨道不平顺的均值向量和协方差矩阵,它们的具体形式如下:
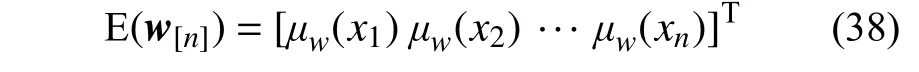
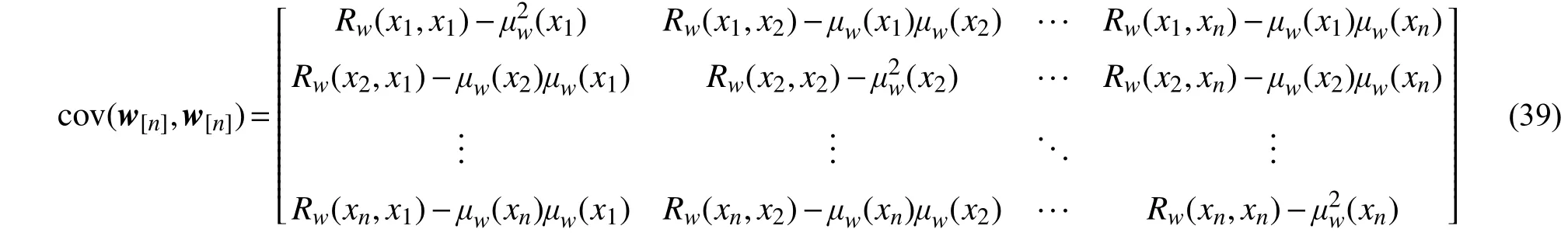
其中,μw(x)和Rw(x,x+τ)分别为轨道不平顺场的均值函数和相关函数。特别地,当w(x)为均匀随机场时,Rw(τ)可由轨道不平顺场的功率谱密度函数Sw(ω)通过傅氏变换求得。
值得注意的是,由式(34)~式(37)计算得到的各协方差矩阵,其对角线元素即为各个时刻磁浮车桥耦合系统关键响应、电流变化量以及悬浮间隙变化量的方差值。
从上述计算列式可以看出,由于已经先行构建了磁浮车桥耦合系统关键响应、电流变化量以及悬浮间隙变化量的显式表达式,在其统计矩的计算过程中,并不需要嵌入磁浮车桥耦合系统运动方程的求解,同时可以针对任意关键响应进行降维计算,显著提高了随机振动的分析效率。由于该法是在时域显式表达式的基础上直接进行统计矩的运算,因此可称为时域显式直接法。
3.2 时域显式随机模拟法
磁浮车桥耦合系统关键响应、控制电流变化量以及悬浮间隙变化量的平均峰值通常也是需要重点关注的,可以利用随机模拟方法获得。根据式(39)给出的轨道不平顺向量w[n]的协方差矩阵,利用随机向量的数字生成方法,如正交分解法[26],即可生成w[n]的大量样本(k=1,2,···,K),K为样本总数。将生成的轨道不平顺样本代入时域显式表达式(24)、式(25)、式(30)和式(31),得:
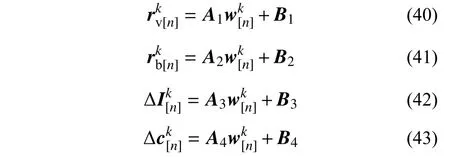
对各个物理量的时程样本峰值进行统计,即可得到各物理量的平均峰值如下:
3.农村新型养老保险。国务院从2009年起开展新型农村社会养老保险(简称新农保)试点。新型农村社会养老保险是以保障农村居民年老时的基本生活为目的,由政府组织实施的一项社会养老保险制度,是国家社会保险体系的重要组成部分。养老待遇由社会统筹与个人账户相结合,与家庭养老、土地保障、社会救助等其他社会保障政策措施相配套,建立个人缴费、集体补助、政府补贴相结合的筹资模式。

值得注意的是,若采用传统随机模拟法,需要将生成的轨道不平顺样本代入电磁力式(9),并借助磁浮车桥耦合系统运动方程式(1)和式(2)进行反复迭代求解,样本分析计算效率很低。利用已经构建完毕的磁浮车桥耦合系统关键响应、电流变化量和悬浮间隙变化量的时域显式表达式进行随机模拟,在样本分析中并不需要求解磁浮车桥耦合系统运动方程,且可以针对任意关键响应进行降维计算,大幅提高了随机模拟的计算效率。由于该法是在时域显式表达式的基础上进行随机模拟,因此可称为时域显式随机模拟法。
4 数值算例1
采用图1 所示的磁浮车桥耦合模型开展数值模拟研究,相关参数参考文[27]选定。桥梁跨度L=20 m , 线密度 ρAb=1.42×103kg/m,抗弯刚度EIb=1.66×108N·m2,采用Rayleigh 阻尼模型,阻尼比 ζ=0.05。桥梁离散为100 个平面梁单元。车体质量m1=500 kg , 电磁铁质量m2=300 kg,车体悬架刚度ks=1.40×104N/m , 车体悬架阻尼cs=5.80×102N·s/m 。 空气磁导率μ0=4π×10-7H/m,有效磁极面积A=0.049 m2,线圈匝数N=356 T,静悬浮电流I0=20 A , 静悬浮间隙c0=0.01 m。电流控制的位移反馈系数G1=7500 A/m,速度反馈系数G2=10 A·s/m , 加速度反馈系数G3=0.5 A·s2/m 。 车辆行驶速度V=20 m/s。
假定轨道不平顺场为零均值均匀随机场,其功率谱密度函数可取为如下形式[5]:
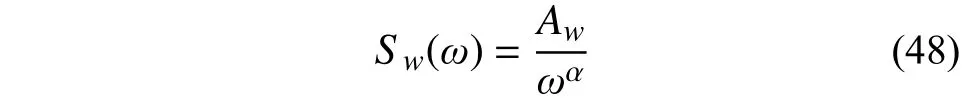
式中:ω为空间圆频率,ω=2πf,f为空间频率;α为频率特征参数;Aw为粗糙度系数。在本算例中,取 α=3,Aw=6.1×10-8m,f的取值范围为[0.01,7]m-1。
4.1 单样本时程分析
根据上述功率谱密度函数形成如式(39)所示的轨道不平顺向量的协方差矩阵,据此生成大量轨道不平顺样本,其中一条轨道不平顺样本如图2所示。
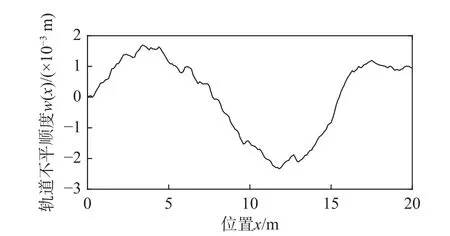
图2 某轨道不平顺样本Fig. 2 A sample of guideway irregularity
采用Newmark-β 积分格式建立磁浮车桥耦合系统关键响应、电流变化量和悬浮间隙变化量的时域显式表达式,分别如式(24)、式(25)、式(30)和式(31)所示,时程分析步长 Δt=0.005 s。考虑图2 所示的单个轨道不平顺样本,采用时域显式法获得桥梁跨中竖向位移ybm、车体竖向加速度a1、电流变化量 ΔI和悬浮间隙变化量 Δc的时程曲线,分别如图3~图6 所示。为了进行对比,采用传统的Newmark-β 逐步迭代法计算得到的结果也示于图3~图6 中。从图中可见,时域显式法和传统方法的计算结果完全吻合,说明了时域显式法的正确性。
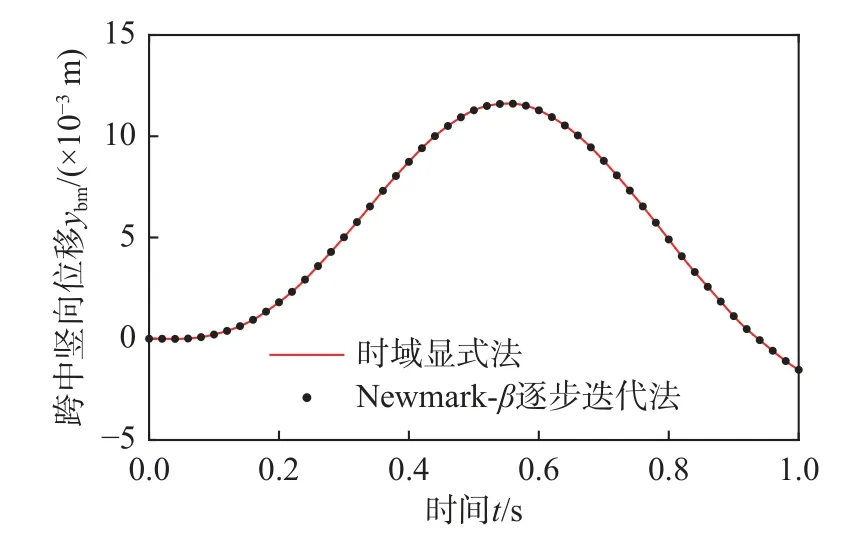
图3 桥梁跨中竖向位移 ybm时程Fig. 3 Time history of vertical displacement ybmat mid-span of bridge
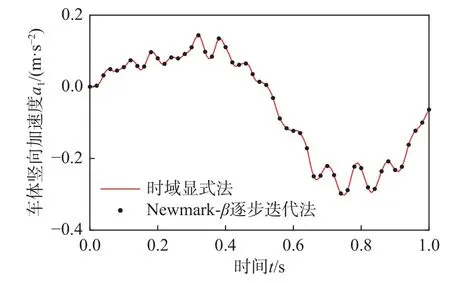
图4 车体竖向加速度 a1时程Fig. 4 Time history of vertical acceleration a1 of car body
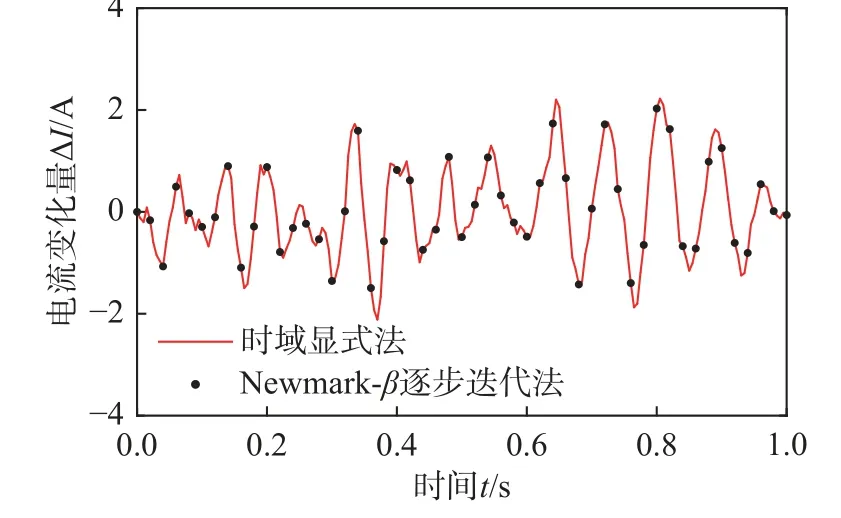
图5 电流变化量 ΔI时程Fig. 5 Time history of electric current change ΔI
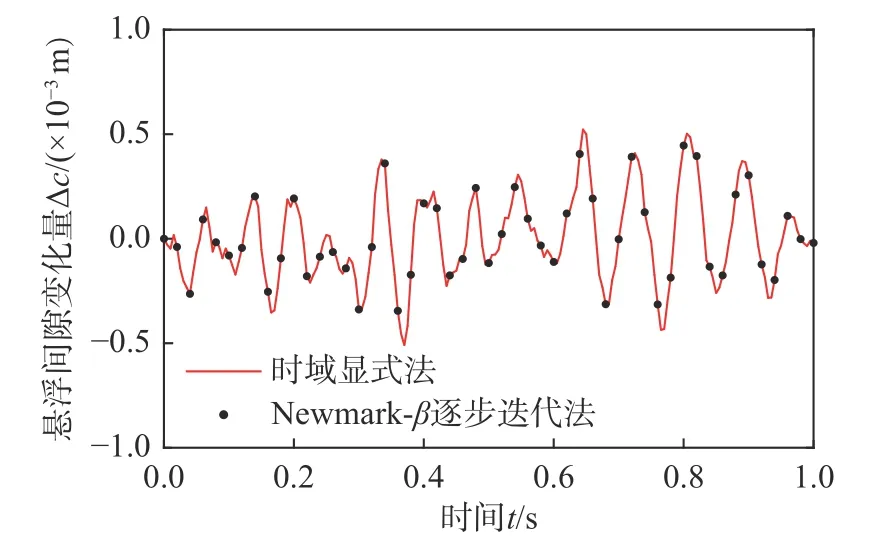
图6 悬浮间隙变化量 Δc时程Fig. 6 Time history of air gap changeΔc
在计算效率方面,表1 对比了两种方法进行单样本分析的计算耗时。从表1 中可见,时域显式法的耗时由两部分组成:一部分是建立时域显式表达式所需时间(0.739 s);另一部分是利用时域显式表达式进行时程分析所需时间(0.013 s),总耗时0.752 s;而Newmark-β 逐步迭代法则耗时1.413 s。显然,对于单样本时程分析,时域显式法的计算效率已经高于Newmark-β 逐步迭代法的效率。

表1 单样本时程分析耗时对比Table 1 Comparison of computation time for sample analysis
4.2 响应统计矩分析
采用时域显式直接法,即式(34)~式(37),计算磁浮车桥耦合系统关键响应、电流变化量和悬浮间隙变化量的统计矩时程。其中,考虑到轨道不平顺是零均值均匀随机场,因此 E(w[n])=0,而cov(w[n],w[n])可以利用式(48)给出的功率谱密度函数计算得到。图7~图14 分别给出了桥梁跨中竖向位移ybm、车体竖向加速度a1、电流变化量 ΔI和悬浮间隙变化量 Δc的均值时程和标准差时程。为了进行对比,根据 cov(w[n],w[n]),通过正交分解法生成大量轨道不平顺样本,采用时域显式随机模拟法进行统计矩分析,其结果也示于图7~图14中。从图中可见,随着样本数的增加,时域显式随机模拟法的计算结果逐渐收敛,并与时域显式直接法的计算结果十分接近,验证了时域显式直接法的正确性。注意到,对于随机模拟,计算电流变化量或悬浮间隙变化量统计矩时程所需样本数一般要多于计算桥梁跨中竖向位移或车体竖向加速度统计矩时程所需的样本数。从图8 可见,在车辆即将出桥时,桥梁跨中竖向位移的标准差出现最大值,这一现象与文[10]算例中出现的情况相似。
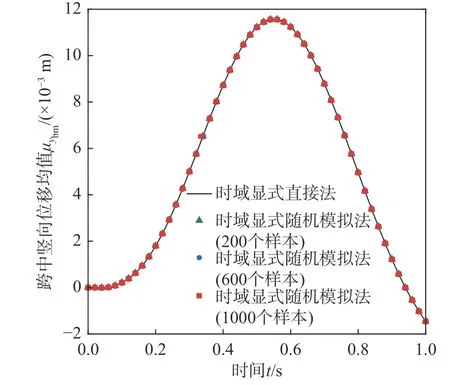
图7 桥梁跨中竖向位移 ybm 均值时程Fig. 7 Time history of mean value of vertical displacement ybmat mid-span of bridge
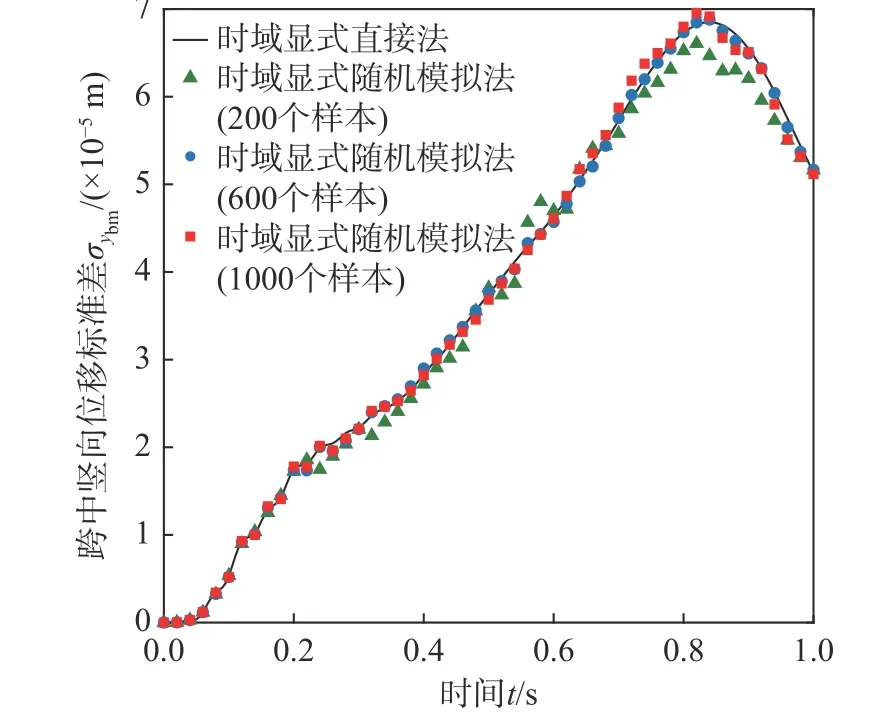
图8 桥梁跨中竖向位移 ybm 标准差时程Fig. 8 Time history of standard deviation of vertical displacement ybm at mid-span of bridge
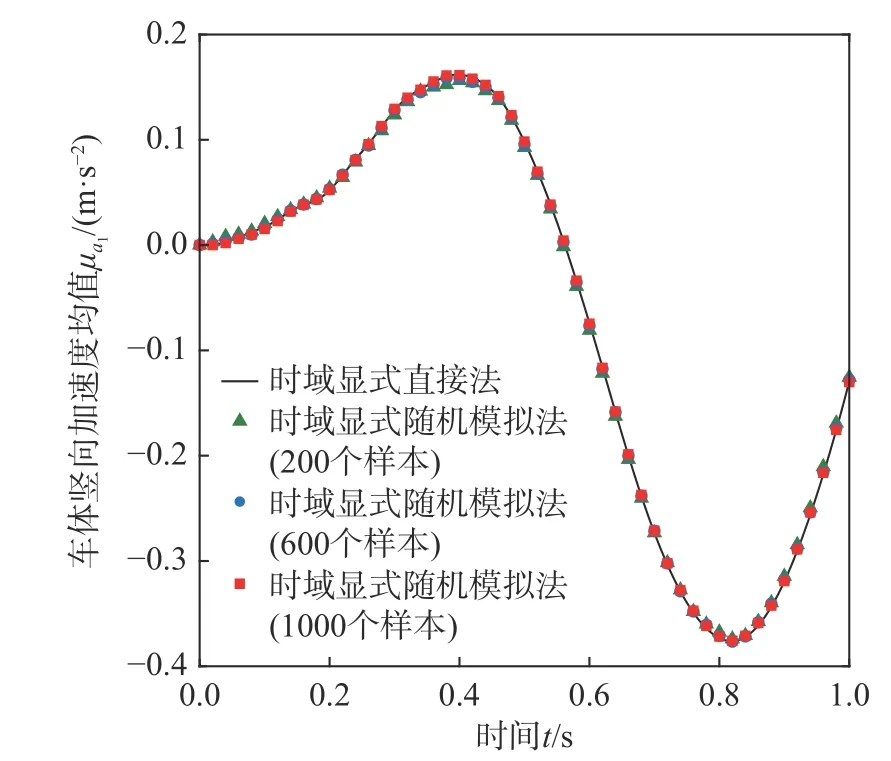
图9 车体竖向加速度 a1均值时程Fig. 9 Time history of mean value of vertical acceleration a1 of car body
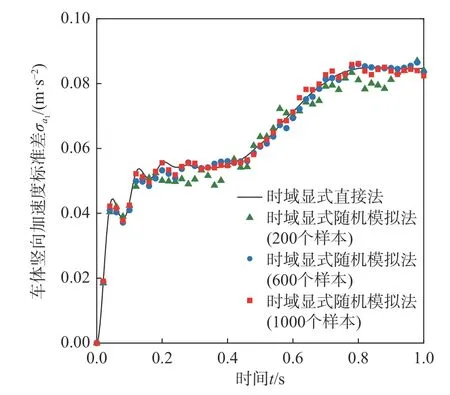
图10 车体竖向加速度 a1标准差时程Fig. 10 Time history of standard deviation of vertical acceleration a1 of car body
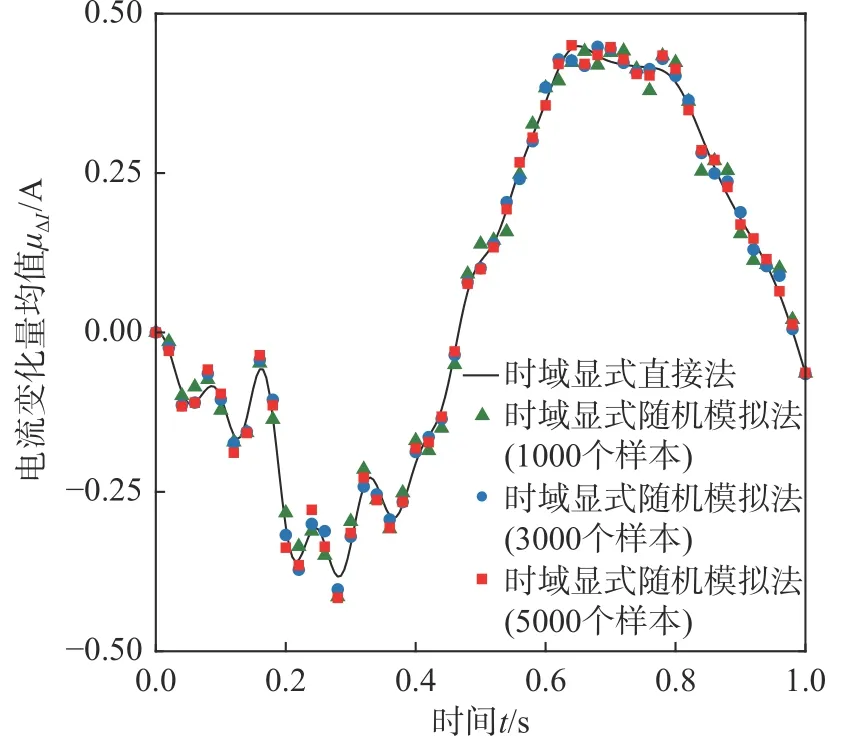
图11 电流变化量 ΔI均值时程Fig. 11 Time history of mean value of electric current changeΔI
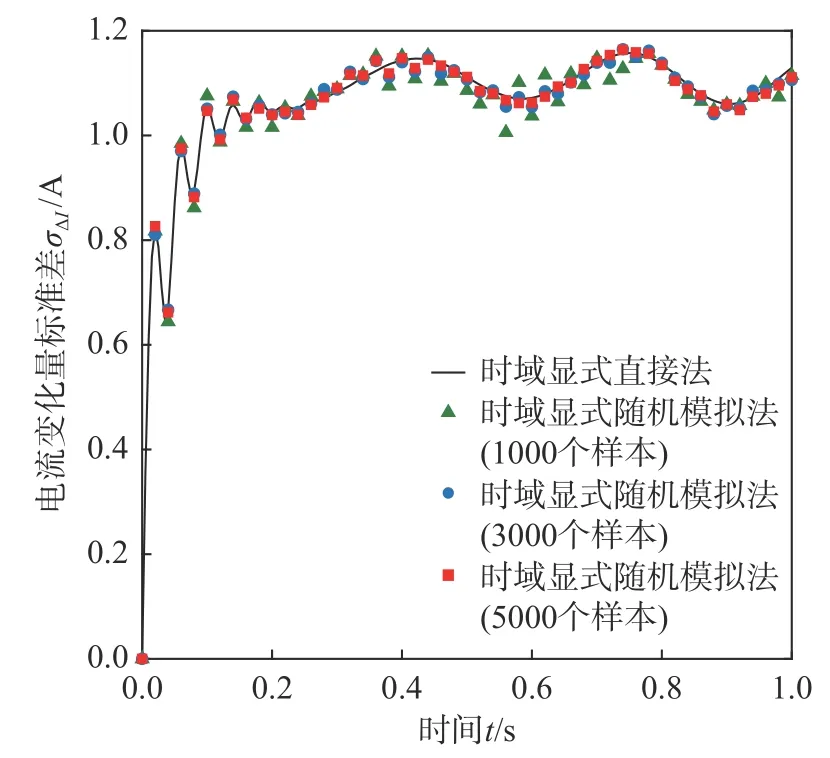
图12 电流变化量 ΔI标准差时程Fig. 12 Time history of standard deviation of electric current changeΔI
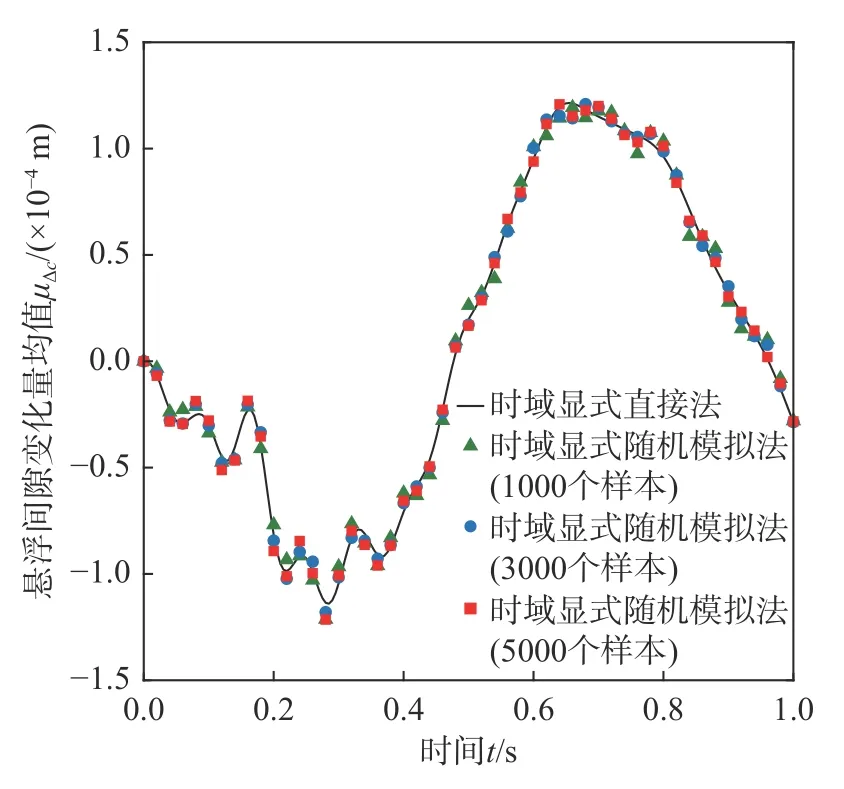
图13 悬浮间隙变化量 Δc均值时程Fig. 13 Time history of mean value of air gap changeΔc
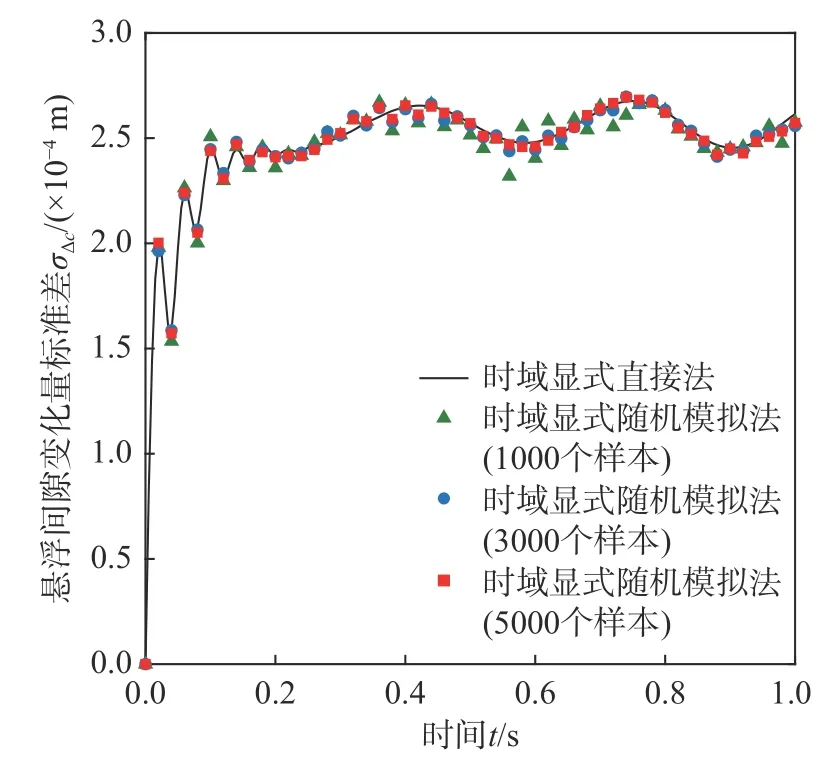
图14 悬浮间隙变化量 标准差时程ΔcFig. 14 Time history of standard deviation of air gap changeΔc
在计算效率方面,表2 列出了两种方法的计算耗时。从表中可知,两种方法都需要建立系统响应时域显式表达式,耗时0.739 s,该时间与表1相应的时间是一致的。除此以外,时域显式直接法在进行响应统计矩运算时,还需耗时0.100 s;而时域显式随机模拟法在进行响应统计矩分析时,还需耗时0.072 s~0.693 s 不等,这部分时间取决于所选的样本数。显然,两种方法均具有较高的计算效率。值得注意的是,随着样本数的增加,时域显式随机模拟法的计算耗时并没有显著增加,这是由于时域显式表达式仅需构建1 次,即可用于各样本分析。因此,样本数的增加对于时域显式随机模拟法的总耗时影响不大,说明在样本数规模加大时,时域显式随机模拟法比传统随机模拟法(如基于Newmark-β 逐步迭代的随机模拟法)更具计算效率优势。
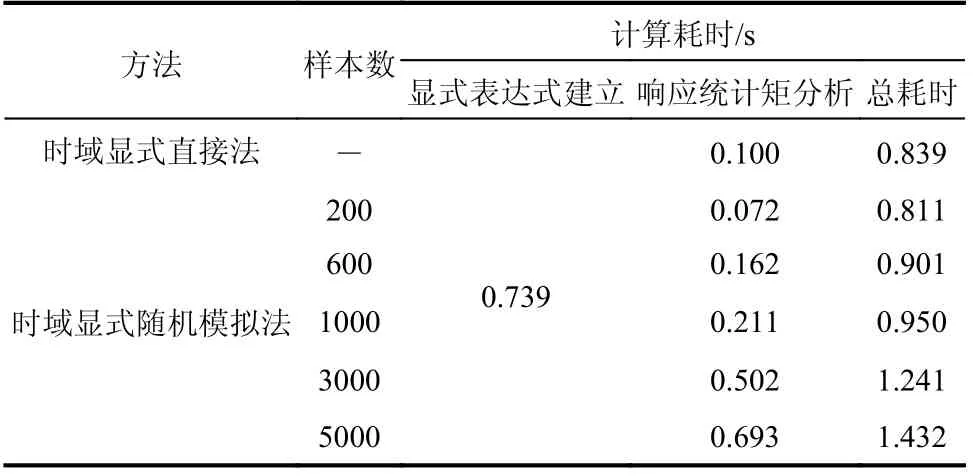
表2 算例1 响应统计矩分析的计算耗时Table 2 Computation time for statistical moment analysis of responses for the 1st numerical example
4.3 响应平均峰值分析
根据 cov(w[n],w[n]),通过正交分解法生成大量轨道不平顺样本,采用时域显式随机模拟法,即式(44)~式(47),分别计算桥梁跨中竖向位移ybm、车体竖向加速度a1、电流变化量 ΔI和悬浮间隙变化量 Δc的平均峰值,其结果如表3 所示。从表中可见,各响应平均峰值收敛较快,当采用200 个样本时,结果已基本收敛。由于表3 中所考虑的样本数与表2 中的样本数一致,这里的时域显式随机模拟法计算时间与表2 所列时间基本一致。
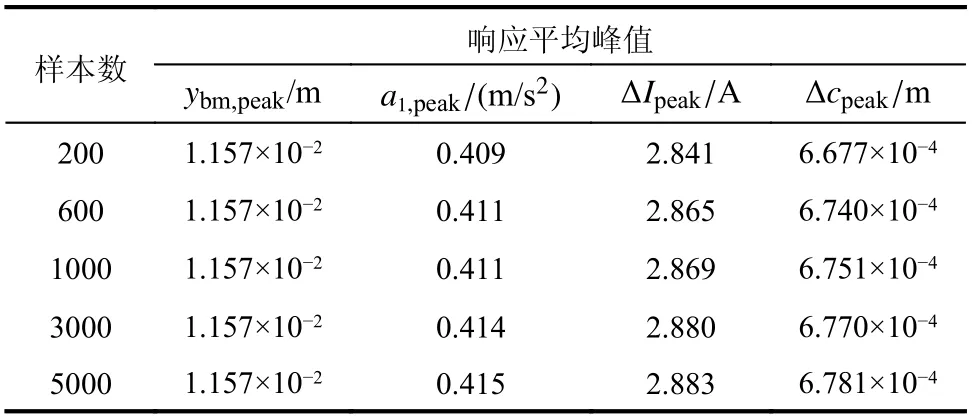
表3 各响应平均峰值Table 3 Mean peak values of responses
5 数值算例2
本文以二自由度磁浮车辆与桥梁耦合模型为例阐述了时域显式法的列式过程,该列式原理同样可以推广应用于多自由度磁浮列车与桥梁耦合系统的随机振动分析。采用图15 所示的磁浮列车过多跨简支梁桥模型开展工程应用研究,相关参数参考文[27]选定。多跨简支梁桥的单跨长度L=25 m , 线密度 ρAb=3.76×103kg/m,抗弯刚度EIb=2.46×1010N·m2,采用Rayleigh 阻尼模型,阻尼比 ζ=0.05。每跨简支梁离散为100 个平面梁单元。磁浮列车由三节车辆组成,每节车辆包含1 个车体和5 个悬浮架,采用多刚体建模,考虑沉浮和点头运动,每节车辆共12 个自由度。其中,车体长度L1=16 m , 车体质量M1=2.32×104kg,车体转动惯量J1=2.11×105kg·m2,悬浮架长度L2=3.12 m , 悬浮架质量M2=846 kg,悬浮架转动惯量J2=1.80×103kg·m2,悬浮架与车体之间由车体悬架连接,车体悬架刚度ks=8.10×104N/m,车体悬架阻尼cs=5.00×103N·s/m。考虑车辆之间的联系,车辆连接竖向刚度kl=5.00×105N/m,车辆连接竖向阻尼cl=2.50×104N·s/m。悬浮架下布置4 个电磁铁,每个电磁铁对应的有效磁极面积A=0.084 m2,线圈匝数N=356 T,静悬浮电流I0=20 A , 静悬浮间隙c0=0.01 m。电流控制的反馈系数取值与数值算例1 相同。列车行驶速度V=100 km/h。
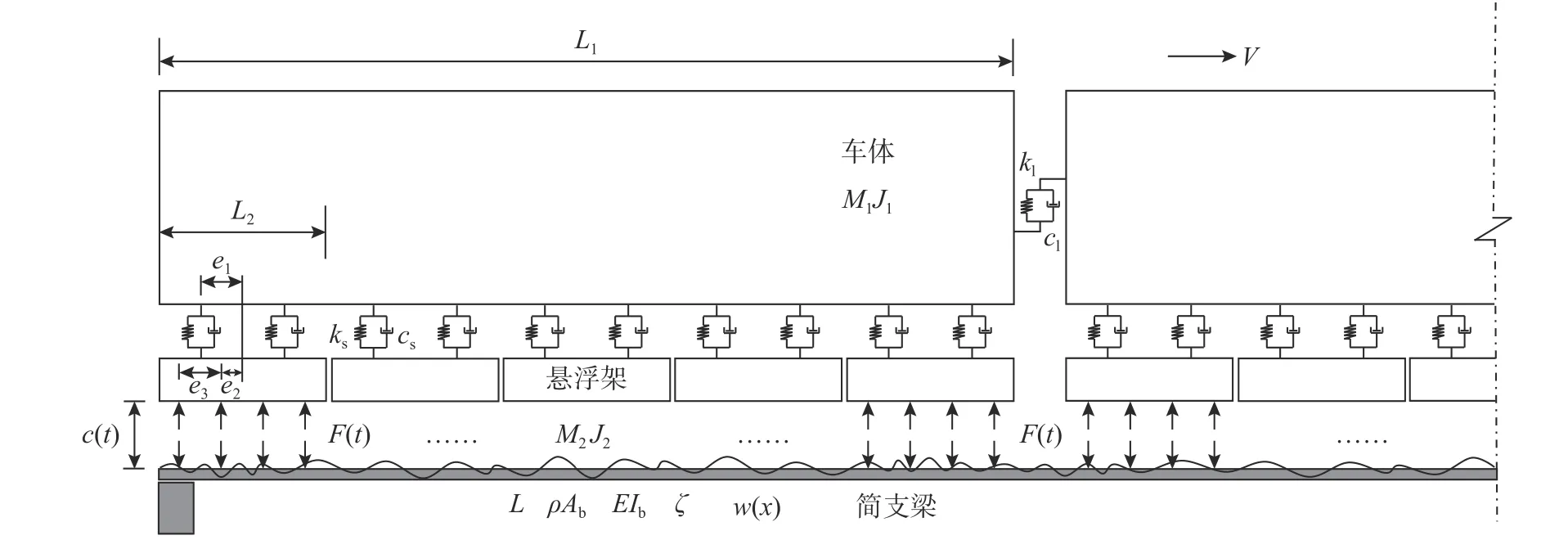
图15 磁浮列车过多跨简支梁桥模型Fig. 15 Mechanical model for a maglev train traversing a multi-span simply-supported bridge
采用与数值算例1 中相同的轨道不平顺场功率谱密度函数,分别利用时域显式直接法和时域显式随机模拟法计算磁浮车桥耦合系统关键响应的统计矩时程,时程分析步长 Δt=0.02 s。图16~图19 分别给出了某跨简支梁跨中竖向位移ybm和第2 节车辆车体竖向加速度a1的均值时程和标准差时程。从图中可见,时域显式随机模拟法采用1000 个样本的计算结果与时域显式直接法的计算结果十分接近。
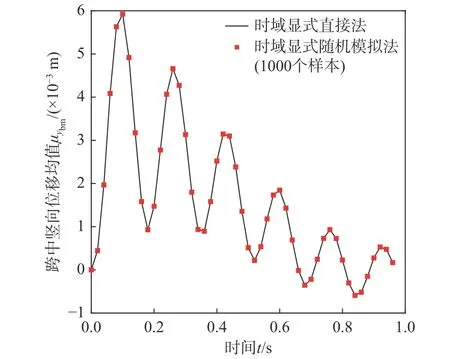
图16 某跨简支梁跨中竖向位移 ybm 均值时程Fig. 16 Time history of mean value of vertical displacement ybmat mid-span of a simply-supported beam
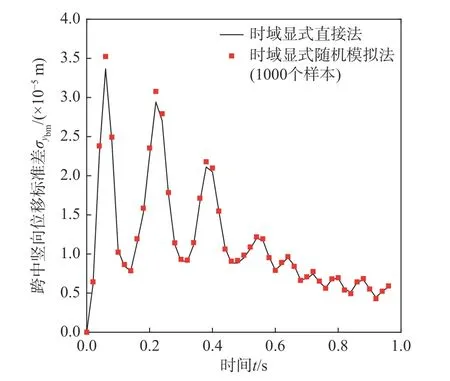
图17 某跨简支梁跨中竖向位移 ybm标准差时程Fig. 17 Time history of standard deviation of vertical displacement ybm at mid-span of a simply-supported beam
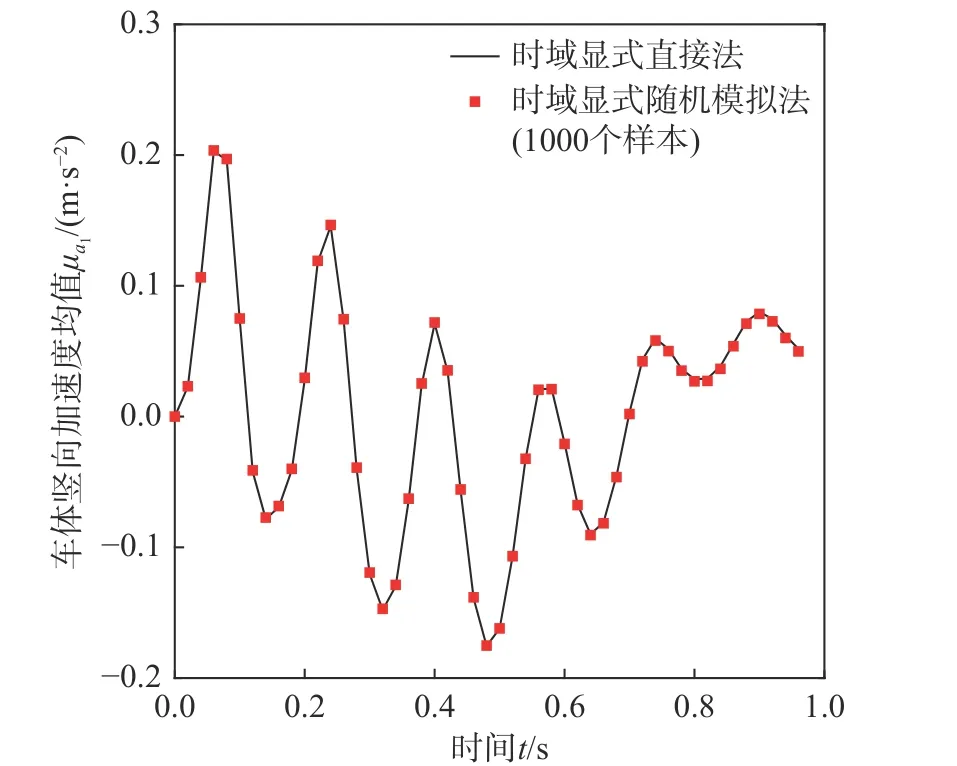
图18 第2 节车辆车体竖向加速度 a1均值时程Fig. 18 Time history of mean value of vertical acceleration a1for car body of the 2nd maglev vehicle
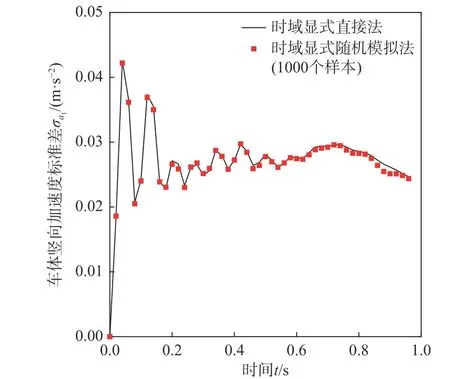
图19 第2 节车辆车体竖向加速度 a1标准差时程Fig. 19 Time history of standard deviation of vertical acceleration a1 for car body of the 2nd maglev vehicle
在计算效率方面,表4 列出了两种方法的计算耗时。从表中可知,两种方法均能对大型复杂磁浮车桥耦合系统进行高效的随机振动分析,其中时域显式随机模拟法比时域显式直接法耗时更短。实际上,当车桥耦合系统规模达到一定程度时,采用式(36)和式(37)所需的计算量将高于采用随机模拟方法所需的计算量,此时时域显式随机模拟法将比时域显式直接法计算效率更高。
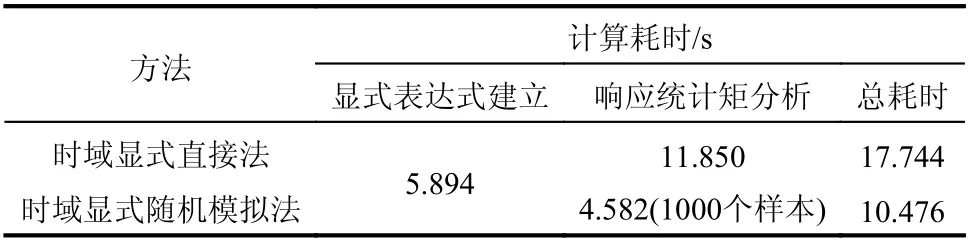
表4 算例2 响应统计矩分析的计算耗时Table 4 Computation time for statistical moment analysis of responses for the 2nd numerical example
6 结论
轨道不平顺作用下磁浮车桥耦合系统随机振动本质上是一类非平稳随机振动,采用传统随机振动方法求解时,由于需要同时处理系统的物理演化和概率演化两种机制,通常需要反复求解磁浮车桥耦合系统的运动微分方程,涉及大量的时程积分运算。本文开展了磁浮车桥耦合系统随机振动分析的时域显式方法研究,得到了以下结论:
(1) 通过建立磁浮车桥耦合系统关键响应关于轨道不平顺的时域显式表达式,完全揭示了系统的物理演化过程,在此基础上再开展磁浮车桥耦合系统关键响应的随机分析,实现了系统物理演化机制和概率演化机制的分离处置;
(2) 时域显式方法大幅提升了磁浮车桥耦合系统随机振动分析的计算效率,可以准确计算磁浮车桥耦合系统关键响应、控制电流变化量以及悬浮间隙变化量等随机过程的统计矩及平均峰值。
本文将电磁力在静悬浮点附近线性化,是一种简化处理。在后续研究工作中,将进一步考虑电磁力的非线性特点,开展磁浮车桥耦合系统非线性随机振动方法的研究,以期在实际工程中推广应用。
——走进广东富华重工制造有限公司

