一维传热方程瞬态问题解析解及其应用
仝 睿,付 浩,宋二祥
(清华大学土木工程系土木工程安全与耐久教育部重点试验室,北京 100084)
浅层土体温度的分布规律,直接影响土体中水分的蒸发、冻结等行为,从而影响到农业生产、岩土工程等领域的研究建设[1-3]。在地表存在公路、铁路等的覆盖层时,冬季土体底部热、顶部冷的温度梯度,还会导致覆盖效应出现[4-7]。如何评价顶部存在覆盖层时,土体温度场的分布,对于探究覆盖效应的发生机理、实现冻土区路基的合理设计具有重要意义。
浅层土体温度常常受太阳辐射、水分蒸发、大气温度等多方面因素影响。但如果将地表温度变化视为正弦变化的温度边界条件,深处恒温土层视为固定的温度边界条件,忽略传热外的其他作用因素,则土层温度分布可以近似为一维瞬态传热问题。徐学祖等[8]在《冻土物理学》中的研究表明:“土体内地温随时间的变化主要是热量输运的影响,数学上可归纳为热传导问题”。传热方程反映的热量输运情况,对地温如何随时间变化有着非常大的影响。因此,研究该一维传热方程的定解,对于估计实际土体内温度场的分布,具有重要的参考价值。
实际土体多为分层材料。每层土体内,物理性质会有波动,但近似为均质材料可以简化计算,且并不会导致较大的误差。在《冻土物理学》中,即有将单一土层视为均质材料,进行热流计算的算例[8]。考虑到传热方程涉及的热容量、传热系数、密度等参数主要受到含水率影响,当土体内含水量随时间变化不大时,将土体简化为均质材料进行分析是可行的。此外,本文随后的推导表明,单一土层的分析,可以进一步推广到分层土模型中。因此,对单一均质土层的一维传热方程定解进行分析,对于工程问题中的多层土层温度变化分析同样具有参考价值。
关于一维传热方程的解析求解,此前已有一定研究。涂新斌等[9],使用复变函数方法,分析了模型无限大,底部不存在恒温点时,一维传热方程对应的解析解。李翊神[10]使用杜哈梅积分法,研究了传热方程定解和波动方程定解之间的关系。王兆瑞等[11]使用傅里叶变换和积分函数表示方法,分析了一维传热方程的特解。林府标等[12]通过李代数,研究了一维广义方程的解析解特点。左冲等[13]使用时域径向积分法给出了积分形式的传热方程解。但是,目前尚未有人给出底部温度恒定、顶部温度变化边界条件下,土体一维瞬态传热问题的解析解。
本文给出一维瞬态传热问题的解析解。通过与数值模拟及现场测试结果的对比验证了解析解的正确性,进而给出了解析解在冻深估计、有关模型试验中几何相似关系的确定、“覆盖效应”数值模拟等方面的应用。
1 一维瞬态传热问题解析解
1.1 解析解推导
土体或上覆材料的顶部,与大气直接接触,可近似用正弦曲线反映顶部空气温度每日或每年的周期性变化。而在底部较深处,则假定温度基本恒定将,土近似为均质材料,得到的控制方程及边界条件为:
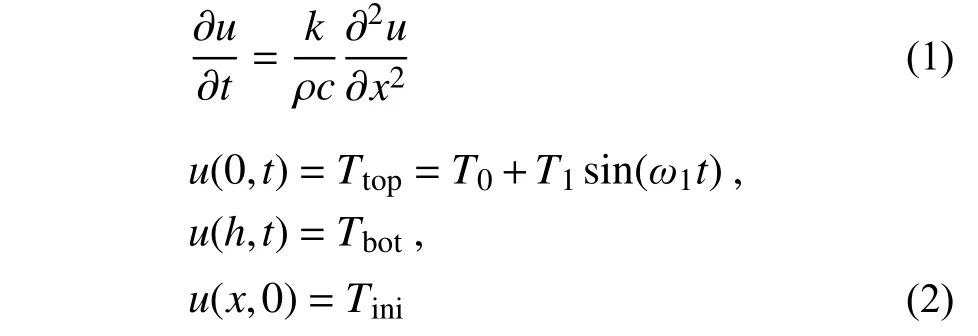
式中:u为单元体温度;ρ 为材料密度;c为材料比热容;k为材料导热系数;T0为顶部温度均值;T1为顶部温度正弦变化部分振幅;Tbot为深层土体恒定温度;Tini为初始状态的温度分布。
式(1)可根据数学物理方程中的参数分离法进行求解[14]:
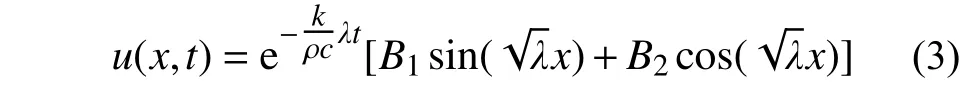
式中:B1、B2为待定系数;λ 为变量分离法选取的常数。
对于顶部与底部的固定值部分,存在对应特解:
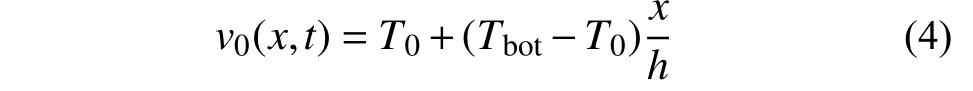
对于顶部的正弦边界条件,设对应的温度解形式为:
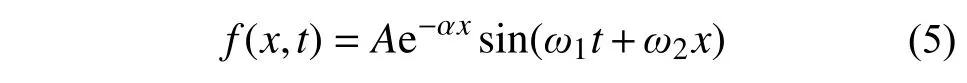
根据特解需要满足的传热方程式(1),解出对应的系数之间的关系:
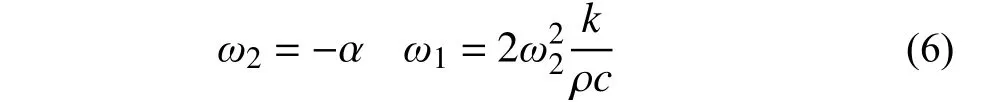
又因为x=0 时,需符合顶部温度边界条件,可以得到对应Tsin(ωx)的特解为:
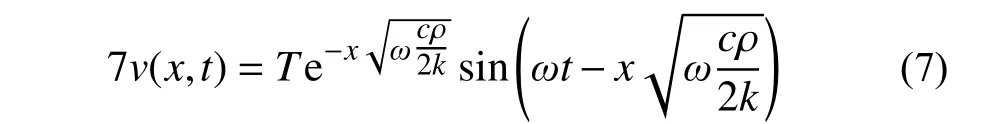
从而,针对非齐次边界条件(2),对应的特解为:
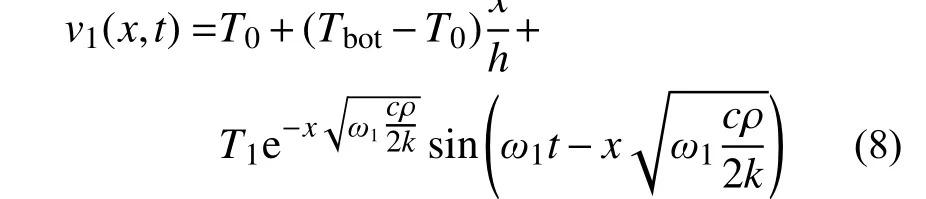
假如初始值条件选取为:
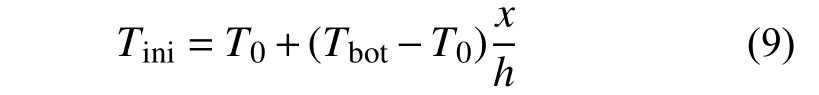
则这组特解反映的是顶部正弦温度边界条件,会形成振幅不断衰减的正弦温度波动,向土体下方传播。
当波动传播到土体底部时,特解式(8)中,取x=h,得到的边界条件无法和底部u(h,t)=Tbot的边界条件相协调,说明特解式(8)并不能同时符合上、下端边界条件。此时需要如图1 所示,叠加函数式(10),才能满足底部的边界条件。
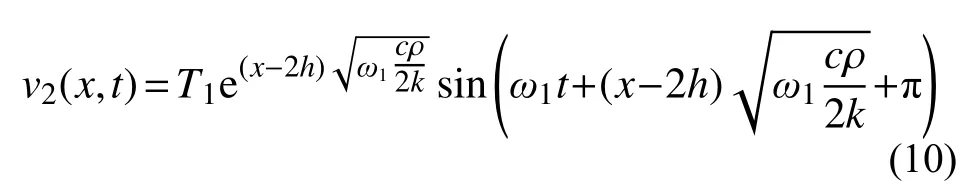
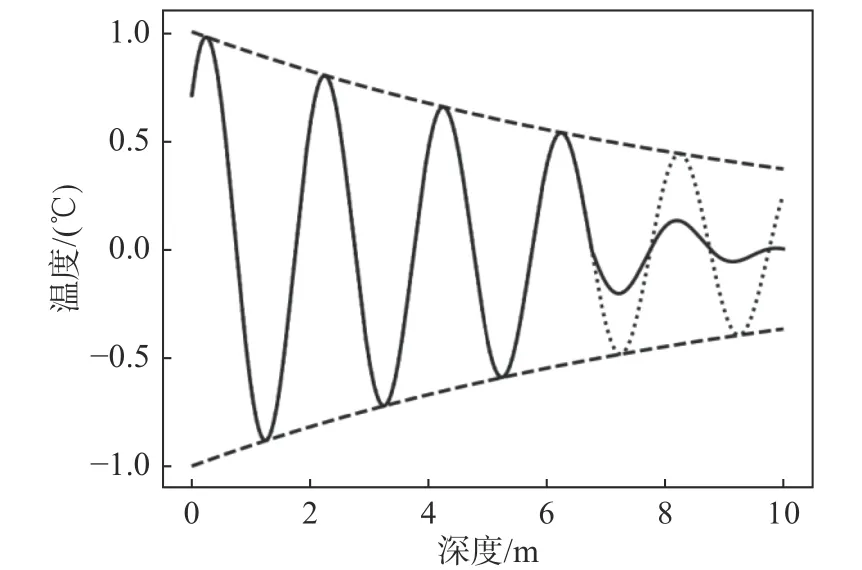
图1 叠加示意图Fig. 1 Composition of functions
而函数式(10)又会导致顶部边界条件无法满足。将反射函数不断叠加下去,最终得到了同时满足上、下边界条件,级数形式的精确解:

这两个无穷级数,都可以通过比较判别法证明绝对收敛。以第一个级数和为例:
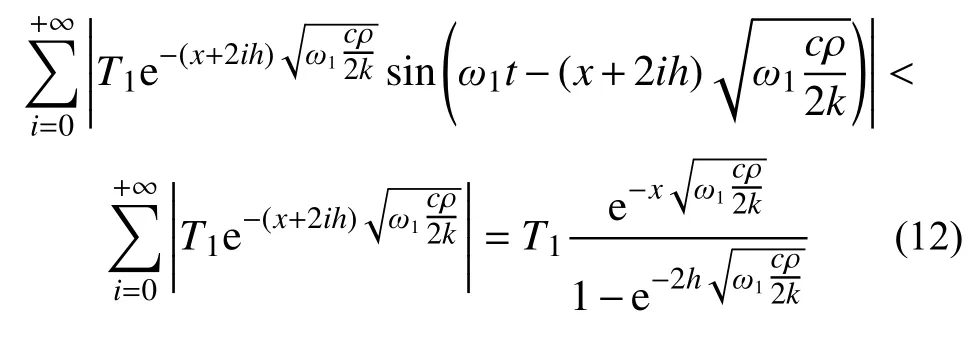
从而可以知道,无穷级数V(x,t)收敛。
注意到精确解(式(11))中,不断叠加的级数项,反映了温度波动变化传播到土体底部时,存在反射现象。反射波动回到土体顶部时,又会再次反射。而且式(10)中,与应力波、光波等波动类似,在固定端反射时,都出现了“半波损失”的现象。
如果给定的初始值条件与式(9)存在差异,不妨设:
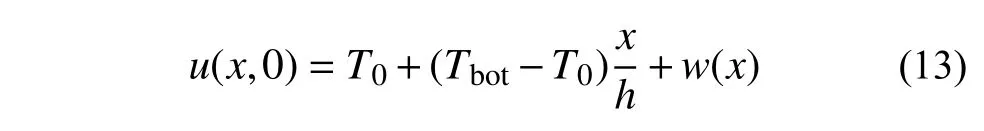
将w(x)以齐次通解式(3)为基底进行傅里叶展开,可以得到对应的齐次解:

其中:
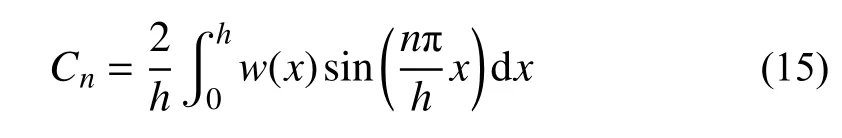
土体或覆盖层顶部的空气温度变化,对应的顶部温度边界条件应当包含每日温度变化、每年温度变化两组正弦变化函数。分别对应:
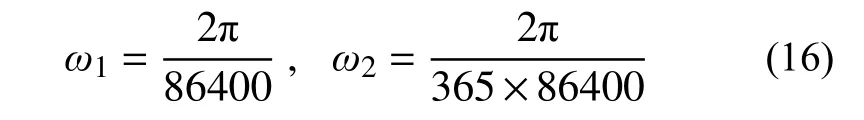
1.2 近似解及其讨论
式(10)给出的精确解,表达形式较为复杂。可以将特殊解式(8),作为精确解式(11)的近似。近似解的相对误差大小为:
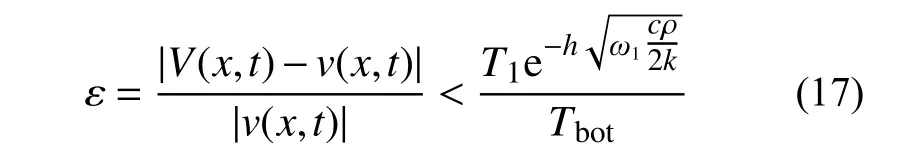
取一组典型数值进行估计。土的密度为1600 kg/m3,比热容1200 J/(kg·K),传热系数k=1.2 W/(m·K),h=20 m,温度年波动T1=20 K,土体底部温度Tbot=278.15 K,此时按式(17)计算相对误差上限约为0.0024%。这意味着,针对自然界中的土体传热问题,式(8)可以很好地近似实际温度变化。
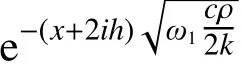
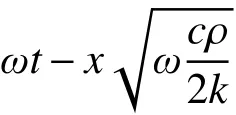
2 解析解的数值验证
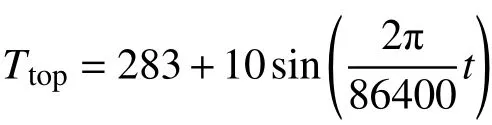

由图2 可见,位于0.1 倍、0.2 倍、0.5 倍波长位置处的土体,在经过1~2 个周期后数值模拟的温度已与解析解接近一致,由此可以看出解析解作为稳态解的正确性。此外,初始时刻温度的差异正说明初始温度场的影响需要一段时间来平衡。
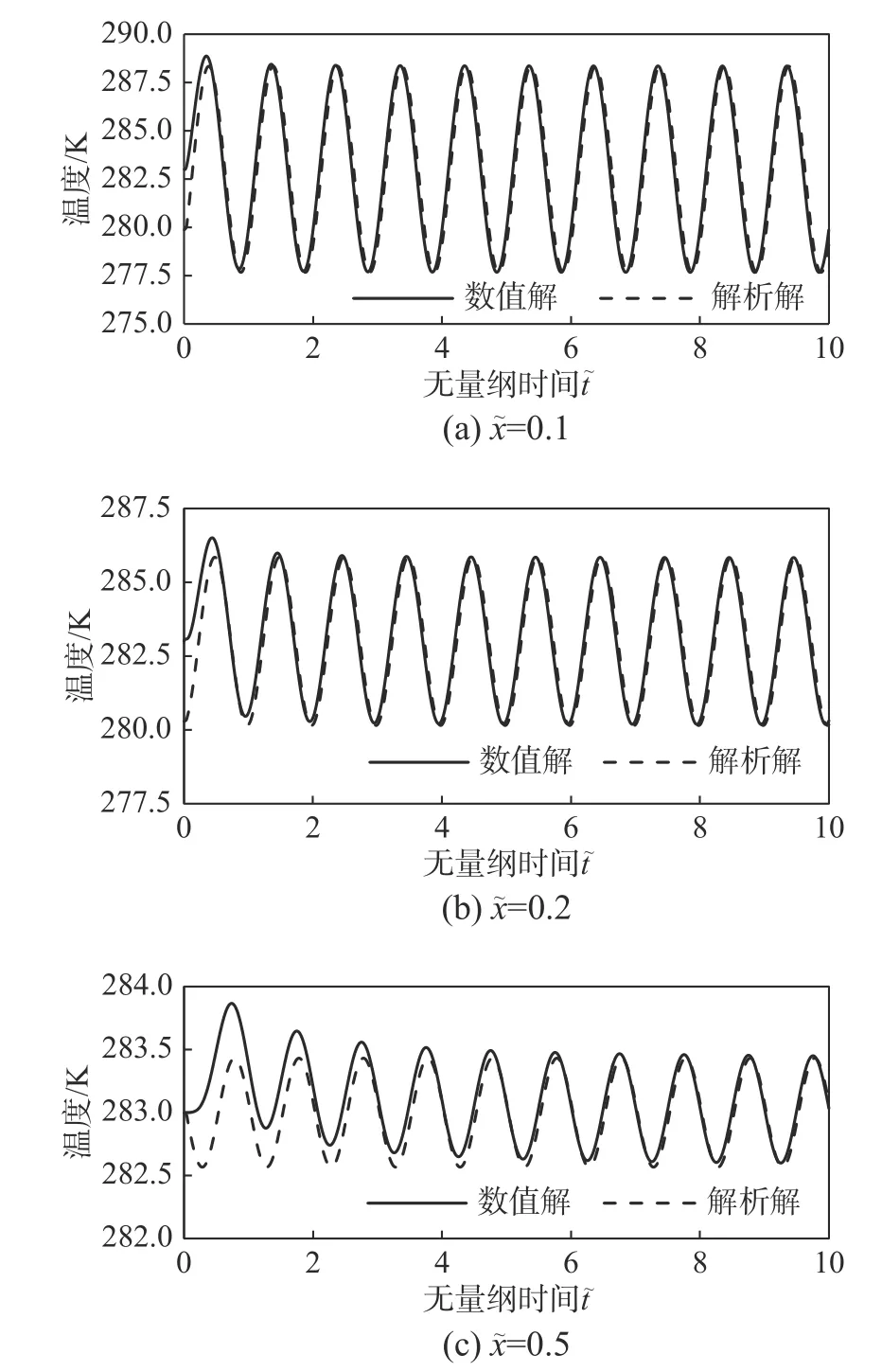
图2 解析解和模拟结果对比Fig. 2 Comparison between analytical solution and simulation results
3 结合现场试验数据对解析解进行验证
本课题组此前在兰新铁路武威段411+600 区域路堤土层中不同深度处布设温、湿度传感器和冻胀计以获得相应的测试数据[15]。
本课题组将监测仪器布置在0.1 m、0.4 m、1.0 m、1.6 m、2.5 m、3.3 m 处,以获得对应深度处的温湿度数据。考虑到2019/06/01~2021/06/01这一时间段内测得的温度数据和2017/11/11~019/06/01 这一时间段内测得的温度数据相差不大,本文选用后一时间段内的温度数据,对解析解加以验证。该时间段内的路基土体温度数据如图3 所示,边坡土体温度数据如图4 所示。

图3 路基土体温度Fig. 3 Temperature of subgrade soil
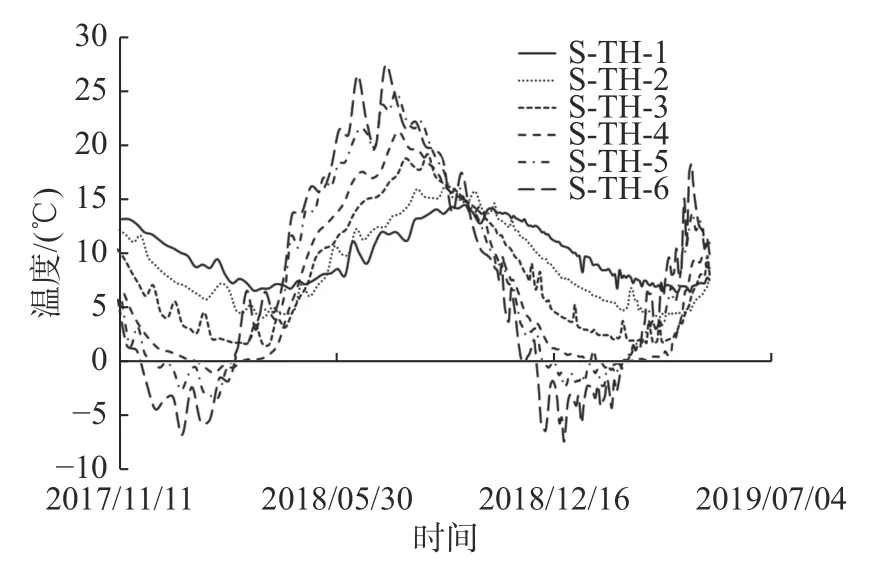
图4 边坡土体温度Fig. 4 Temperature of slope soil
观察图3 和图4 可以发现,土体不同深度处的温度都近似以正弦函数的形式周期性变化。正弦函数的振幅随着深度的增加不断减小,相位随深度增加也存在明显的“滞后性”现象。
3.1 振幅衰减验证
根据不同深度处土体的最高温、最低温计算温度变化的振幅,进而根据振幅的与深度的关系,对解析解进行验证。
路基中土体温度的振幅如图5 所示。使用指数拟合公式进行回归,得到如下公式:
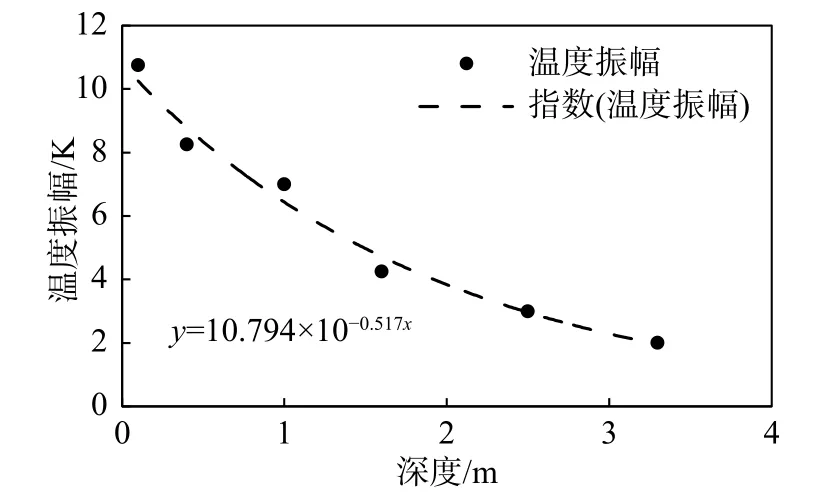
图5 路基振幅-深度关系图Fig. 5 Amplitude vs depth diagram of subgrade
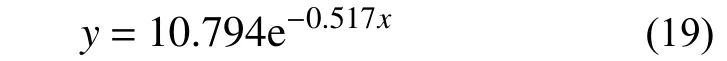
该回归公式的R2为0.9881,回归的效果较好。根据此前测得的土体密度1600 kg/m3,比热容按照1200 J/(kg·K)进行估计,回归参数对应的土体传热系数为:
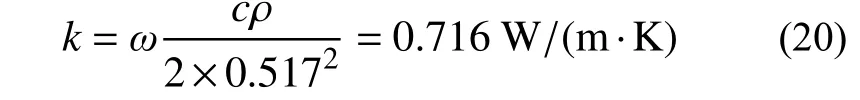
该取值在粉土正常传热系数范围0.6 W/(m·K)~1.4 W/(m·K)之内。
边坡中土体温度的振幅如图6 所示。
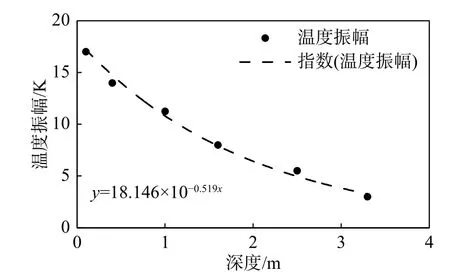
图6 边坡振幅-深度关系图Fig. 6 Amplitude vs depth diagram of slope
使用指数拟合公式进行回归,得到下式:
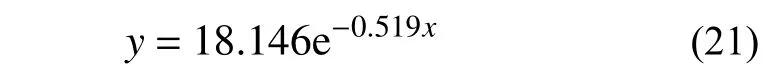
该回归公式的R2为0.989。根据此前测得的土体密度1600 kg/m3、比热容按照1200 J/(kg·K)进行估计,回归参数对应的土体传热系数为:
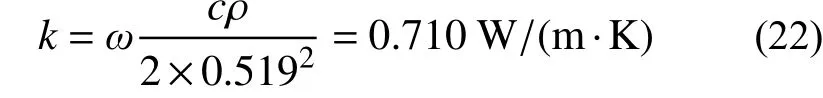
与根据路基中温度变化情况回归出的土体传热系数极为接近。
根据式(19)和式(21)可以得到,路基顶部的石砟层,将大气温度变化衰减为:
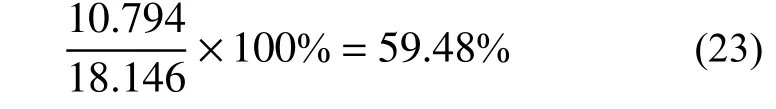
根据铁道部数据,石砟表观密度在2700 kg/m3左右,堆积密度1500 kg/m3左右。据此推算,路基顶部石砟层孔隙率在44.4%左右。石砟层厚度按照平均值0.65 m 计算。石砟比热容按照1000 J/(kg·K)计算。空气导热系数为0.023 W/(m·K),石砟导热系数取为1.28 W/(m·K)。估算得到的等价导热系数为:
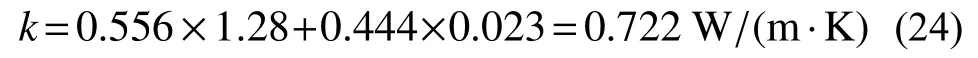
根据这个估算的年温度变化衰减为:
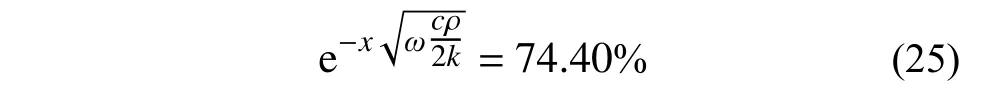
这一估计数值与式(23)的实际计算数值存在较大的差距。存在差距的原因将在第四节最后进行解释。
3.2 相位滞后性验证
将不同传感器测得最高温的时间点,与传感器的深度进行回归,从而对解析解进行验证。
路基中土体取得最高温的时间点如图7 所示。其中纵轴的数值(时间/d),代表传感器自2017 年11 月11 日开始测量数据以来,经过了多少天测得了最高温数据。使用线性拟合公式进行回归,回归得到如下公式:
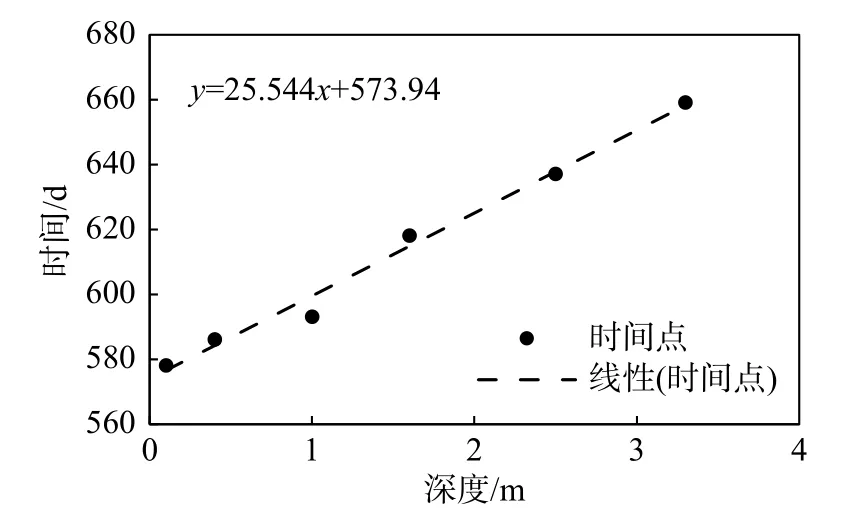
图7 路基最高温时间点-深度关系图Fig. 7 Maximum temperature time vs depth diagram of subgrade
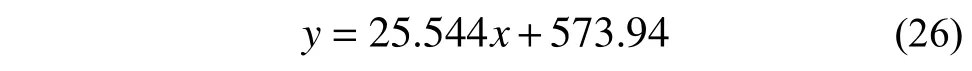
该回归公式的R2为0.9883,回归的效果较好。根据此前测得的土体密度1600 kg/m3,比热容按照1200 J/(kg·K)进行估计,回归参数对应的土体传热系数为:
这个取值在粉土正常传热系数范围0.6 W/(m·K)~1.4 W/(m·K)之内。
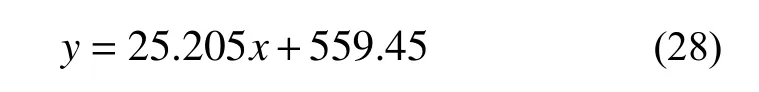
边坡中土体取得最高温的时间点如图8 所示。使用线性拟合公式进行回归,回归得到公式:该回归公式的R2为0.9793。根据此前测得的土体密度1600 kg/m3,比热容按照1200 J/(kg·K)进行估计,回归参数对应的土体传热系数为:
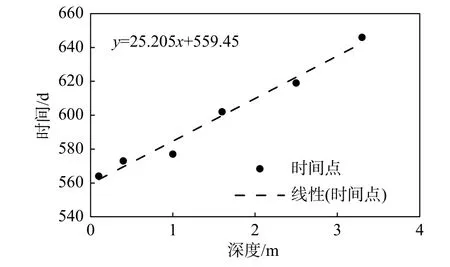
图8 边坡最高温时间点-深度关系图Fig. 8 Maximum temperature time vs depth diagram of slope
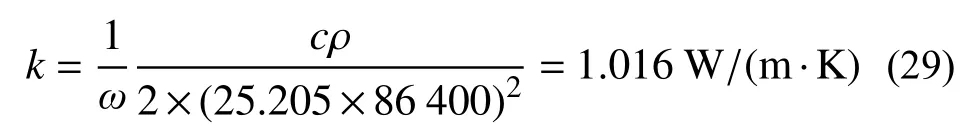
这个取值在粉土正常传热系数范围0.6 W/(m·K)~1.4 W/(m·K)之内。
值得注意的是,根据相位滞后性反推的土体传热系数,不论路基和边坡,都明显高于根据振幅衰减情况反推得到的土体传热系数。
观察到温度变化的传播函数与波的传播函数类似,且式(11)推导了固定温度边界产生的反射波存在,及其对应的“半波损失”现象。笔者有一个猜想:“温度变化传播到不同性质材料的交界面上,也会发生反射和入射现象,带来振幅的改变”,笔者将在后文对这一猜想加以证明。
4 不同性质材料交界面的反射函数推导
考虑两种不同材料交界面处情况,其中,上方材料厚度为x1、密度为ρ1、热容量为c1、传热系数为k1,下方材料厚度为x2、密度为ρ2、热容量为c2、传热系数为k2,温度边界条件设为:
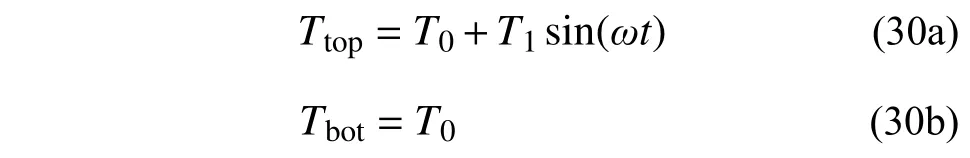
初始值条件设为:

参考式(7),从t=0 时刻开始,顶部正弦温度变化逐渐向下传输。而当温度传输到交界面上时,需要在交界面上同时满足温度的连续性条件,以及热流量的平衡条件。
假设上方入射温度方程为:
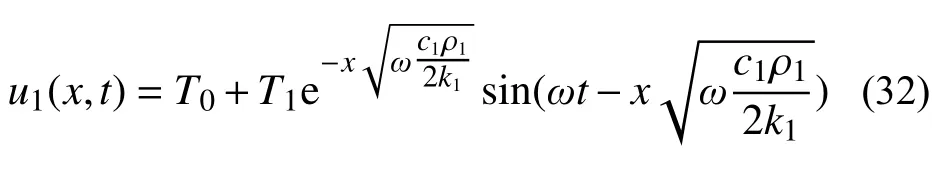
假设入射后温度方程为:
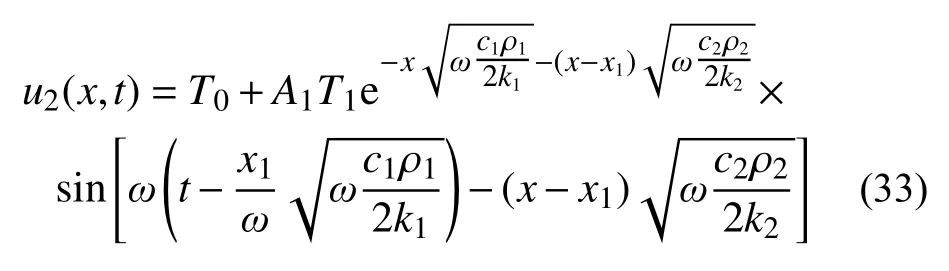
观察到热流量:
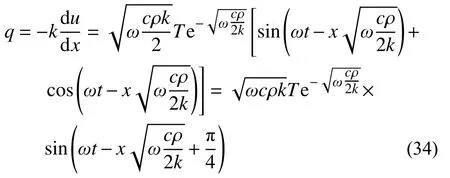
如果只存在入射现象,则可以得到方程:
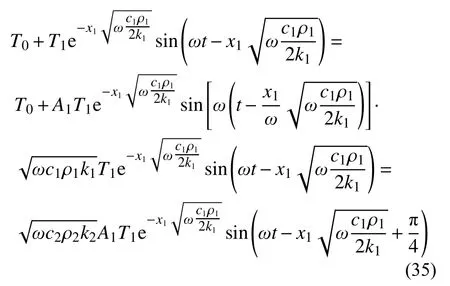
由式(35)中的第一个温度连续性方程可知,未知参数A1=1。代入第二个热流量平衡方程,可以看到,除非两种材料的c、ρ、k值相等,不然热流量平衡方程肯定无法满足。
与振动波、光波类似,这里可以取cρk这一乘积值作为表征材料对热量传输能力的参数。
当两种材料的值cρk不同时,为同时满足交界面处的温度连续性方程、热流量平衡方程,就需要引入反射波。假设反射波方程为:

从而在交界面处,得到方程:

化简为:
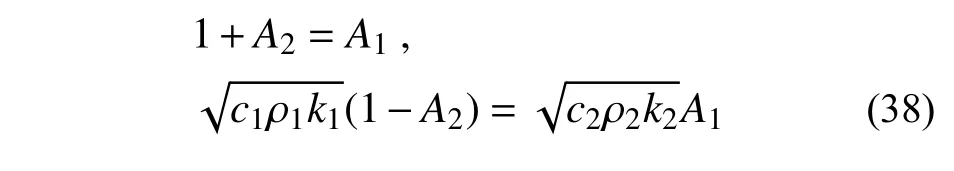
从而可以解出:
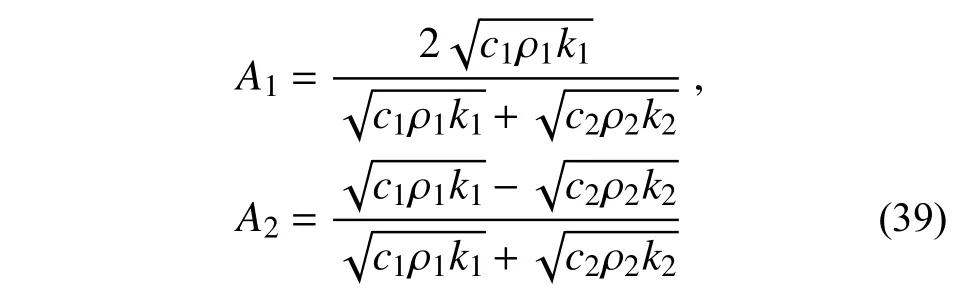
从解式(39)可以看出,反射温度函数的振幅一定小于入射温度函数。当温度函数从cρk值比较大的材料传入cρk值比较小的材料时,入射后温度函数的振幅会大于入射前温度函数的振幅,同时反射温度函数的振幅系数为正。而当温度函数从cρk比较小的材料传入cρk值比较大的材料时,入射后温度函数的振幅会小于入射前温度函数的振幅,同时反射温度函数的振幅系数为负,存在“半波损失”现象,如图9 所示。
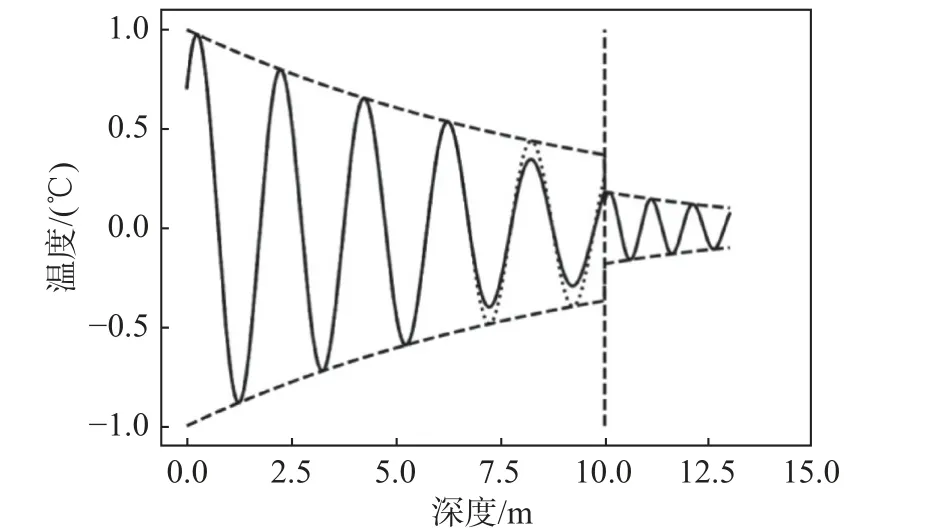
图9 不同材料交界面反射示意图Fig. 9 Reflection in interface between different materials
从本节的推导中可以看出,温度函数的振幅变化会受到不同材料交界面的影响。而相位变化,则不会受到不同材料交界面的影响。因此,式(28)、式(29)根据相位变化回归得到的热传导系数,更接近于真实的土体平均热传导系数。
而式(26)估算得到的比率,明显小于实际衰减后的振幅比率,也是因为没有考虑交界面处反射波。如果将交界面处的反射波纳入考虑之中,将土体传热系数按照式(28)估计为0.989 W/(m·K)。重新估算得到的衰减后比率为:
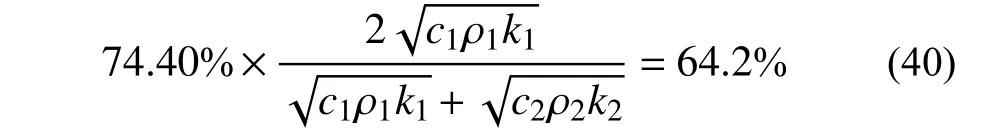
这一比率略大于实际值59.48%。考虑到实际石子与石子之间不是完全贴合,石砟层的传热系数应略小于按照空气、石子并联估算的式(24),式(40)得到的比率略高于实际值,属于较为合理的结果。
5 反射函数的数值模拟验证
使用COMSOL 对解得的反射函数进行验证。上方材料厚度为x1=1 m、密度为ρ1=1200 kg/m3、热容量为c1=1400 J/(kg·K)、传热系数为k1=1.0 W/(m·K),下方材料厚度为x2=1 m、密度为ρ2=1400 kg/m3、热容量为c2=1600 J/(kg·K)、传热系数为k2=1.0 W/(m·K)。温度边界条件设为:
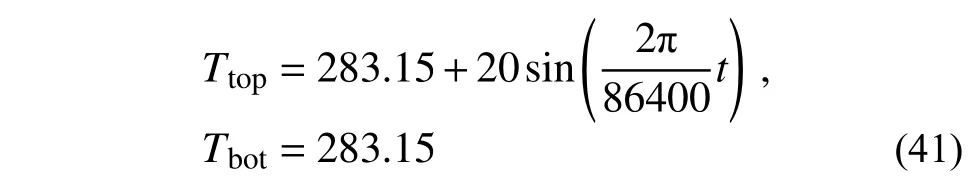
初始值条件设为:

模拟到10.25 d 时,交界面附近的数值解、解析解如图10 所示。补充了忽略热流量平衡方程得到的无反射波参考解作为对比。
图10 中,仿真结果与理论分析结果基本一致,而无反射对应解则存在明显偏差。
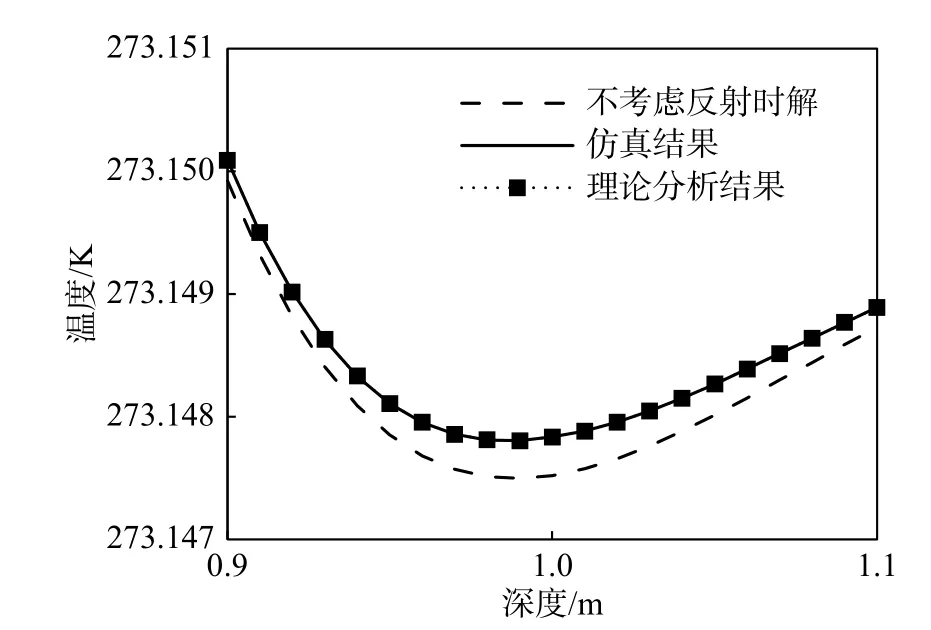
图10 仿真结果与理论分析结果对照图Fig. 10 Comparison of simulation result and analytical result
6 解析解的应用
6.1 使用解析解对冬季冻深进行估计
假设某地区地大气温度变化遵循公式:
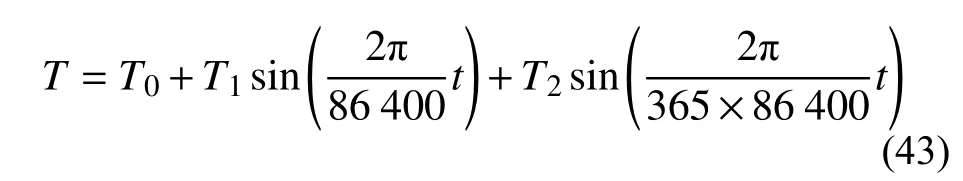
考虑完全裸露均质土体,忽略衰减较多的日温侵入。在地下x/m 处对应的温度为:
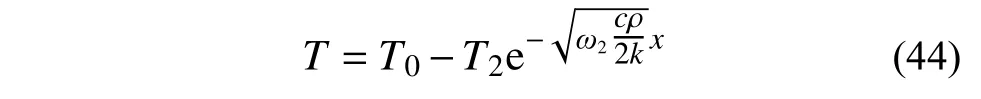
求解T>273.15 K,得到:
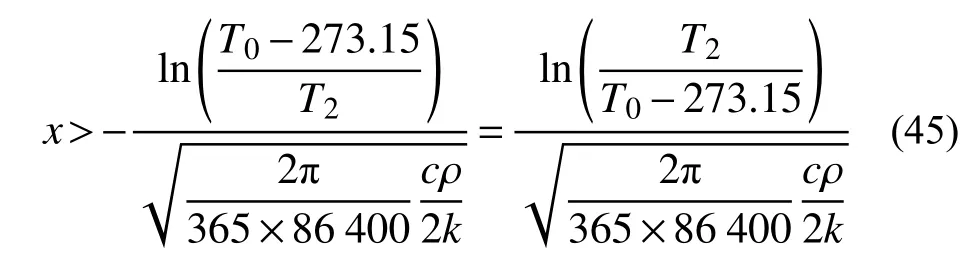
以西安地区为例,文献[15]测得西安地区粉质粘土比热容为1231.6 J/kg·K,传热系数为1.9885 W/(m·K),密度为1959.184 kg/m3。西安地区平均温度T0为288.65 K,年温度变化振幅约为18.5 K。根据式(45)估算,冻深为:
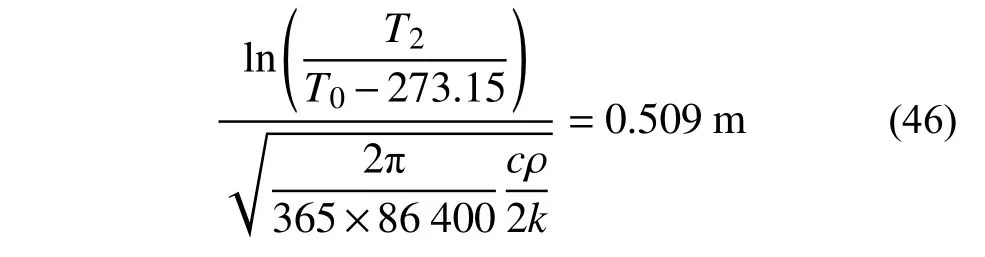
查阅相关文献[16]知,西安地区冬季观测到的冻土深度为0.45 m。估计的冻深与实际的冻深相比,误差为20%。考虑到实际情况土层并非是均匀介质,且土体内水分迁移、化学反应等因素对于土体的温度分布会产生影响,这一误差较为合理。20%的误差,可以满足估测的需要。
6.2 使用解析解估计室内试验的“尺寸效应”
在使用小尺寸样本对实际大尺寸情况进行试验模拟时,一个常见的问题是:顶部温度条件如何选取,才可以模拟实际自然界中的温度变化情况。
例如,室内试验装置高度1 m,用于模拟实际10 m 深的土体温度变化。则对应的,模拟年温度变化的室内试验顶部温度变化周期,应当选取为365/100=3.65 d。
6.3 使用解析解对“覆盖效应”模拟条件进行修正
此前针对“覆盖效应”现象的数值模拟,顶部边界往往直接设置为大气温度变化[4,17-18];或者设置为固定温度[19]。实际情况下,顶部道面也会对大气温度变化有折减和滞后作用。考虑这一情况,根据顶部道面情况,对覆盖效应的顶部边界条件进行修正。
例如,沥青道面常见厚度为0.2 m,沥青密度为1200 kg/m3、比热容为1300 J/(kg·K)、导热系数为0.7 W/(m·K),下方土层密度为1600 kg/m3、比热容为1200 J/(kg·K),导热系数为1 W/(m·K)。
此前本课题组的论文[4]中,选择顶部模拟条件为:年平均温度为283.15 K、日温度变化振幅为10 K、年温度变化振幅为15 K。
考虑交界面处的反射现象计算得到的日温度变化,经过沥青道面衰减为:
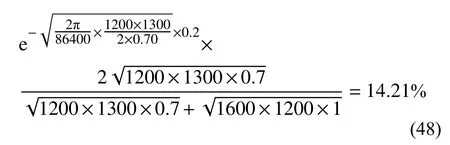
年温度变化衰减为:
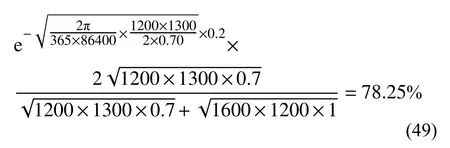
对应的,修正后大气温度变化条件近似为:
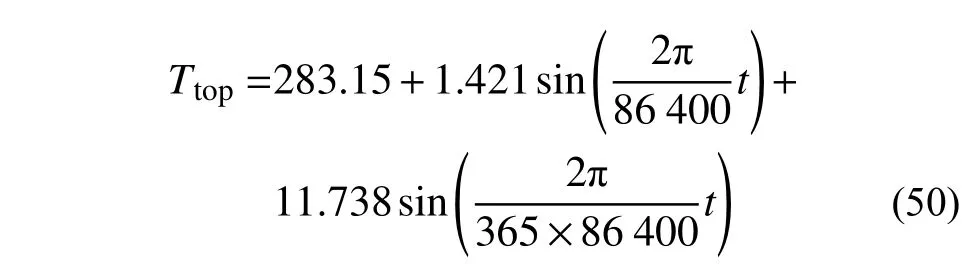
除了顶部温度边界条件外,从第1 节也可以看出,模拟需要设置合理的初始值条件。实际土体经过多年顶部温度作用,土体内温度分布已经近似于式(9),因此,模拟的初始值应按照式(9)进行设置,才可以得到较为接近实际情况的水热迁移结果。
从式(10)可知,模型高度需要满足:
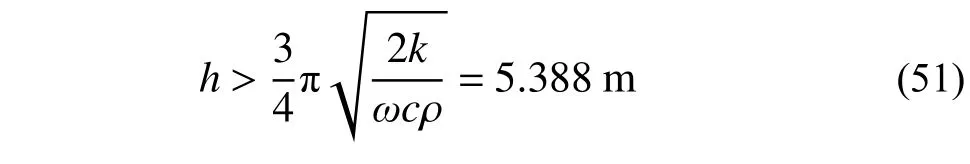
才可以忽略底部固定边界条件产生的反射波影响。因此,将模型高度修改为10 m。
修正前,模型的初始值条件为全域288.15 K。修正后的初始值条件设计为:
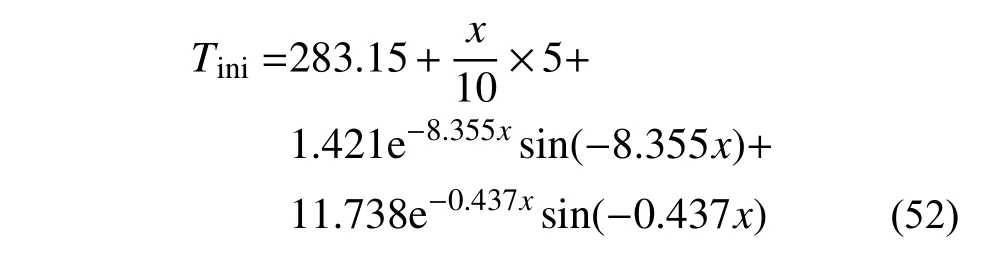
其余模拟参数按照文献[4]进行设置。
修正前、后冬季温度对比如图11 所示。
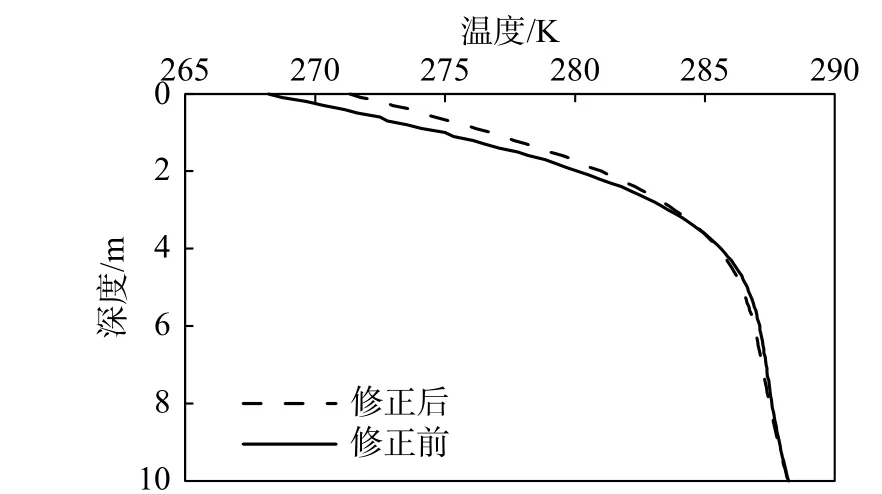
图11 修正前、后温度对比图Fig. 11 Temperature comparison before and after modification
从图11 中可以看出,修正后土体温度波动更小,冬季顶部温度更高。
修正前、后含水量对比如图12 所示。
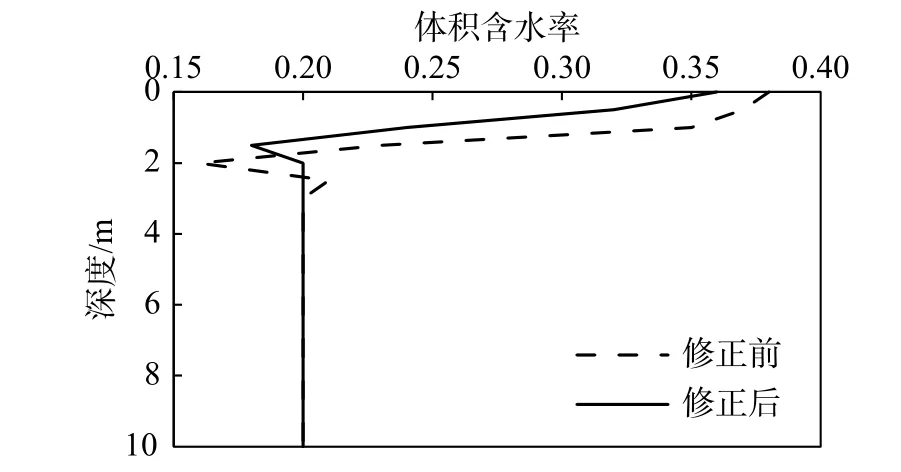
图12 修正前、后含水量对比图Fig. 12 Water volumetric content comparison before and after modification
从图12 中可以看出,修正后,土体顶部的水分聚集更少。
修正前、后的结果对比表明:修正前的模型,夸大了路基土体顶部的温度变化幅度,得到的水分迁移量偏大,对“覆盖效应”影响的预测偏大。
7 结论
本文针对一维土柱的瞬态问题,求解了对应的解析解。通过数值模拟、现场试验两种方式验证了解析解的正确性。本文还推导了解析解在固定边界处、不同材料交界面上存在的反射现象。通过对推导结果的分析,发现:
(1) 土体顶部温度正弦变化带来的土体温度改变与应力波存在一定相似性,会以波动的形式向下传播;但波动振幅在传播过程中会以指数形式不断衰减。
(2) 温度正弦变化的传播在固定边界处存在带有“半波损失”的反射现象;在不同材料交界面处也存在反射现象。
(3) 该解析解存在多种应用场景。可以根据该解析解,估计土体某一深度处的温度变化情况;估计冬季冻结深度;计算室内试验满足“尺寸效应”的合理边界条件;计算土体顶部以上存在覆盖层时,对应的顶部温度边界条件。

