三维效应对超声速湍流燃烧流动大涡模拟的影响研究

刘宏鹏

国防科技大学 空天科学学院，湖南 长沙410073

近几十年来，随着电子计算机在运算速度与数据存储技术上的迅速发展，以及数值计算方法的进步，计算流体力学（CFD）已被广泛应用到超声速湍流燃烧流动的基础研究和工程设计中[1-3]。在数值模拟研究中，当前普遍采用的是雷诺平均（RANS）方法，该方法早已成功用于工程实际的复杂流动模拟，但只能给出流场的统计平均量，无法给出流动细节。直接数值模拟（DNS）虽然可给出全时、空域的详细瞬时流动过程，但由于受到计算机条件与计算方法的制约，在现阶段只适用于具有简单几何边界的较低或中等雷诺数下的湍流流动模拟。近些年来，介于RANS和DNS之间的大涡模拟（LES）方法广被应用于超声速湍流燃烧流动的模拟研究中[4-14]。

为节约计算量，国内外均出现应用二维LES研究超声速湍流燃烧的工作。如D.Chakraborty等[15]采用二维隐式LES 研究了不同化学反应机理对超声速湍流燃烧混合层数值模拟结果的影响。Y.L.Zhang等[16]、C.Qian等[17]分别对超声速湍流燃烧混合层流动开展了二维LES研究，重点观察了火焰的点火、传播、熄火及火焰不稳定等现象。Z. X.Ren等[18-19]采用二维LES研究了超声速湍流燃烧多项流中漩涡、激波和燃烧放热等物理化学现象的相互干扰。这些研究可定性地揭示部分湍流的物理特性，但在实际应用中难以提出可靠的数据。三维属性可对湍流场的数值模拟产生重要影响：P.A.Davidson 在其论著[20]中指出，三维湍流中至关重要的漩涡拉伸作用在二维流动中将失效，由此导致二维湍流呈现出独特特性；此外，M.Breuer[21]具体对比了绕圆柱不可压缩流动的二维/三维LES结果，发现忽略三维效应后，圆柱尾流区的速度分布、分离区大小以及圆柱物面的压强（压力）、摩阻系数分布以及背压系数均产生较大误差。尽管三维效应对于湍流非定常数值模拟极其重要已成为共识，但以往研究大多集中于分析三维效应对于无反应湍流流动数值模拟准确性的影响及其机理。在超声速湍流燃烧领域，由于高马赫数湍流和燃烧间的强烈耦合相互作用，二维LES模拟导致的湍流场结果的误差必然影响燃烧场的数值模拟结果的准确性，使得二维湍流燃烧场呈现独特特性，而关于二维/三维超声速湍流燃烧LES 模拟结果的详细对比研究并不多见。

综上所述，本文旨在探究三维效应对于超声速湍流燃烧流动LES 数值模拟准确性的影响。本文介绍了控制方程，对一个对流马赫数Mac=0.61 的超声速湍流燃烧混合层流动分别开展了二维/三维LES研究，通过对比二维/三维结果分析了三维效应对LES准确模拟超声速湍流燃烧流动的重要性。

1 计算方法

笛卡儿直角坐标系下的考虑多组分燃烧化学反应的质量加权滤波后的Navier-Stokes（N-S）控制方程组包含组分输运、质量守恒、动量守恒和能量守恒方程，分别为

式中：ρ，ui，p与T分别为气体的密度、速度、压力与静温；E为单位质量总能量

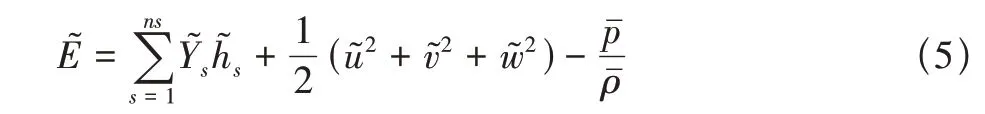
式中：ns为组分总数，Ms、Ys、Ds、hs与ω̇s分别为组分s的摩尔质量、质量分数、质量扩散系数、单位质量的绝对焓值以及单位时间、单位体积的化学反应质量源项，式(1)中的Sct,s为组分s的湍流施密特数，在本研究中取为0.9。需要进一步说明的是，为确保组分质量分数之和为1，通过1 减去其余组分质量分数之和而求得最后一组分的质量分数，即

在本文中，采用氢气-空气的7 组分(H2, O2, H2O, H,O, OH, N2) 8 反应模型[22]化学反应机理模拟燃料为氢气的超声速湍流燃烧混合层流动，最后一组分选定为氮气N2。͂分别为分子黏性应力项和热量扩散项

式中：μ和μt分别为为混合气体分子[动力]黏度和亚格子涡黏度，λ为混合气体的热传导系数，Prt为湍流普朗特数，取为0.5。此外，通过分子动理论[23]获得各组分的分子黏度、热传导系数、质量扩散系数，进而通过Wilke的混合律[24]得到混合气体的分子黏度、热传导系数、质量扩散系数。采用关于温度的多项式拟合获得各组分的定压比热容和静焓，拟合系数见参考文献[25]。为封闭控制方程组，需要加入气体状态方程

式中：M为混合气体的相对分子质量，Ru=8314J/(kmol·K)为普适气体常数。为亚格子雷诺应力

通过Smagorinsky模型模化亚格子雷诺应力，公式为

2 超声速湍流燃烧混合层流动二维/三维LES对比研究

2.1 算例描述及其验证

超声速湍流燃烧混合层流动的来流条件[16]选取典型的超燃冲压发动机燃烧室内来流条件，见表1，其中空气来流马赫数为3.0，温度为1100K，燃料选为氢气和氮气的混合物，以接近声速的速度（Ma=1.13）与空气掺混。混合层流动示意图如图1 所示，其中x，y，z分别表示流向、法向和展向。对流马赫数定义为其中下标1和2分别表示空气和燃料来流，c表示声速。通过表1计算可知本文研究的混合层Mac=0.61。此外，基于入口动量厚度的雷诺数Reθ=2226。

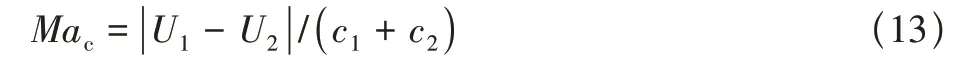
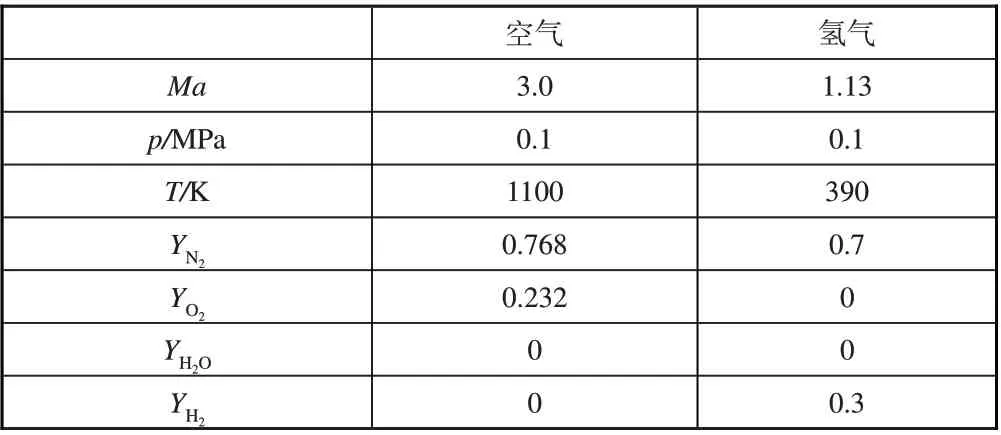
表1 超声速混合层燃烧数值试验自由来流条件Table1 Freestream conditions for computational experiment of supersonic turbulent combustion for a mixing layer flow

图1 超声速混合层燃烧数值试验流动示意图Fig.1 Schematic of supersonic turbulent combustionflow for a mixing layer flow

入口边界配置双曲正切函数型[26]的流向速度分布：

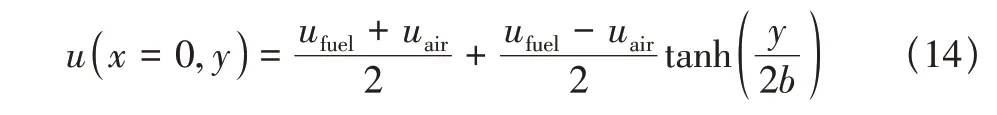
式中：b为控制参数，取为4×10-4m，法向v和展向速度w均为0。为刺激失稳，在入口边界处除了配置时均速度外，额外增加白噪声扰动[26]的脉动速度分量，扰动幅值为0.01uair。此外，如图1 所示，出口为超声速出口边界条件，展向采用周期边界条件。

二维LES 所采用的网格计算域尺寸为1.2m（流向）×0.3m（法向），网格分布为1024（流向）×256（法向），流向网格均匀分布，法向网格在空气流和氢气流的交接处加密。将二维网格向展向拉伸0.15m，并均布128个网格点获得三维网格。网格示意图如图2所示。

图2 x-y平面网格示意图(为使图清晰，x、y方向网格点数均缩小一倍)Fig.2 Schematic of computational mesh at x-y center plane(Every 2th point is displayed at both streamwise and transverse directions for clarity)

对流无黏格式采用5 阶PPWEON-Z 格式[27]，黏性项采用2阶中心差分格式进行离散。时间推进采用双时间隐式迭代方法[28]，时间步长设定为1×10-7s，内迭代步数为5 步。数值模拟采用氢气-空气的7 组分(H2, O2, H2O, H, O, OH,N2)8反应模型[22]。首先计算推进两倍最大通流时间T=2Lx/(U1+U2)得到充分发展湍流流场，然后统计6 倍最大通流时间得到湍流统计相关量[29]，其中Lx=1.2m 为流向计算域尺度。作者在参考文献[27]将三维LES结果与DNS结果进行了对比，发现LES计算获得的雷诺切应力及流向、法向脉动速度均方根分布等与DNS结果相当，验证了本文所采用的数值方法的可靠性和准确性。

2.2 流动和火焰结构

基于氢原子H的混合分数定义为

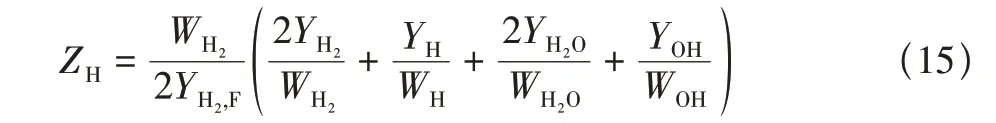
化学当量值Zst=1/(1+S)=0.088,其中S=rYH2,F/YO2,A=10.345。在该算例中，YH2,F=0.3 为燃料一侧来流中氢气的质量分数，YO2,A=0.232为空气一侧来流中氧气的质量分数，r=8为H2/O2充分燃烧时的质量比。图3对比了二维/三维LES的瞬时温度分布，其中温度云图中的黑色曲线为ZH=Zst等值线。由图3可见，无论二维还是三维LES，燃烧均主要发生在ZH=Zst周围。然而，二维LES 下的流动结构以及火焰形态却明显与三维LES结果不同：在流动结构上，二维LES计算获得的流动图像呈现明显的旋涡卷起、分裂和破碎等变化，与Zhang 等[16]、Wang等[30]、Lele等[31]研究采用二维LES/DNS获得的流动图像一致，而三维LES计算获得的湍流流动结构呈不规则状，与Edwards等[32]的三维RANS/LES结果相似；在火焰形态上，二维LES的火焰偏薄，呈条带状，而三维LES 的火焰呈厚的扩散状。图4对比了二维/三维LES 瞬时H2O 质量分数分布。由图4 可见，二维/三维LES 的自点火位置大致相同，约位于x=0.5m 处，且瞬时H2O的质量分数峰值均在0.2以上。

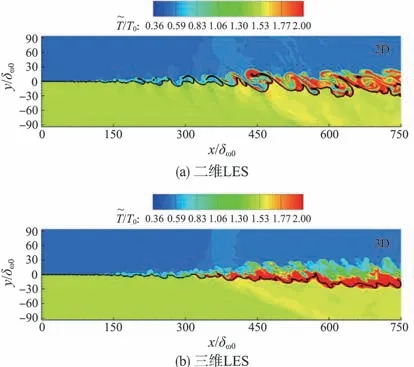
图3 二维/三维LES的瞬时温度分布Fig.3 Instantaneous temperature contours for 2D/3D LES

图4 二维/三维LES的瞬时H2O质量分数分布Fig.4 Instantaneous mass fraction of H2O contours for 2D/3D LES

2.3 湍流旋涡与火焰相互干扰

图5 对比了二维/三维LES 下的涡量分布。由图5 可见，二维/三维LES 的涡量形态显著不同：二维LES 的涡量呈明显的螺旋状表征涡的生成、卷起、并对和破碎；而三维LES涡量呈不规则状。可压缩情况下（忽略外力）的涡量方程的张量形式为

图5 二维/三维LES的涡量Fig.5 Vortex contours for 2D/3D LES

式中：DΩ/Dt表示随体导数，Ω=▽×u为涡量，μv为第二黏度。为简化讨论，假设流体不可压且在二维情况下，式(16)退化为

式(17)表明此时涡量的演化仅受扩散作用的影响。涡量演变的重要支配项，即涡管的拉伸和压缩机制(Ω⋅∇)u由于空间维度自三维退化为二维而失效，因而造成了图5所示的二维/三维湍流涡量场的显著区别。

图6 显示了二维/三维LES 计算获得的涡量、质量分数及OH 化学反应速率的等值线。其中，质量分数等值线范围为0.008 ≤ZH≤0.4，包含化学当量值Zst=0.088，相应也包含高温火焰区域。OH 生成速率等值线范围取为ω̇OH=10～100(kg/m3)/s，为高OH 生成速率区域。由图6 可见，二维/三维情况下，高温火焰区域与高OH生成速率区域一致。火焰形态受涡量场影响而呈现不同形态：二维情况下，受旋涡运动影响，燃烧场也呈现出涡的卷起、并对和破碎等现象；而三维情况下，燃烧场呈不规则状。

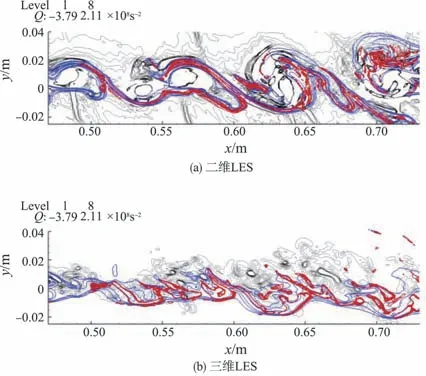
图6 二维/三维LES的湍流旋涡和火焰相互干扰Fig.6 Flow pattern for interactions between turbulent vortex and combustion flames

2.4 混合层厚度增长率

定义δ0、δω和δθ分别为边界层名义厚度、涡量厚度和动量厚度，表达式如下

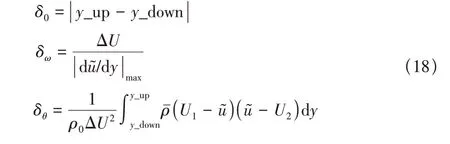
式中：y_up 和y_down分别表示速度U1-0.1ΔU(无量纲值为0.9)和U2+0.1ΔU(无量纲值为0.1)所对应的y向坐标。在动量厚度的定义中，积分上下限通常分别为Ly/2 和-Ly/2。而在当前研究中，其分别以y_up 和y_down替代，原因是空间发展的超声速湍流燃烧混合层流动的点火将诱导激波，激波使得混合层外流动速度降低而与来流条件不一致，混合层分布[y_up,y_down]以外的动量厚度积分将“污染”整体积分值。

图7 给出了二维/三维LES 计算获得的混合层厚度沿流向发展结果，各厚度均以入口处的值作无量纲化。由图7可见，二维/三维LES计算得到的三种混合层厚度具有相同的发展趋势，在点火位置（约位于x/δω0=375）前有一段近似线性的发展区域，点火位置附近区域混合层厚度呈非线性发展，在点火位置后同样有一段近似线性的发展区。点火位置后的混合层厚度近似线性发展区域中，无量纲湍动能分布在不同流向站位处的趋于一致，如图8所示。因此，可判定该区域为流动自相似区。采用最小二乘法对流动自相似区的混合层厚度进行线性拟合，两种模式给出的三种混合层厚度增长率见表2。由表2 可知，二维LES 给出的自相似区三种混合层厚度增长率均明显低于三维LES结果。

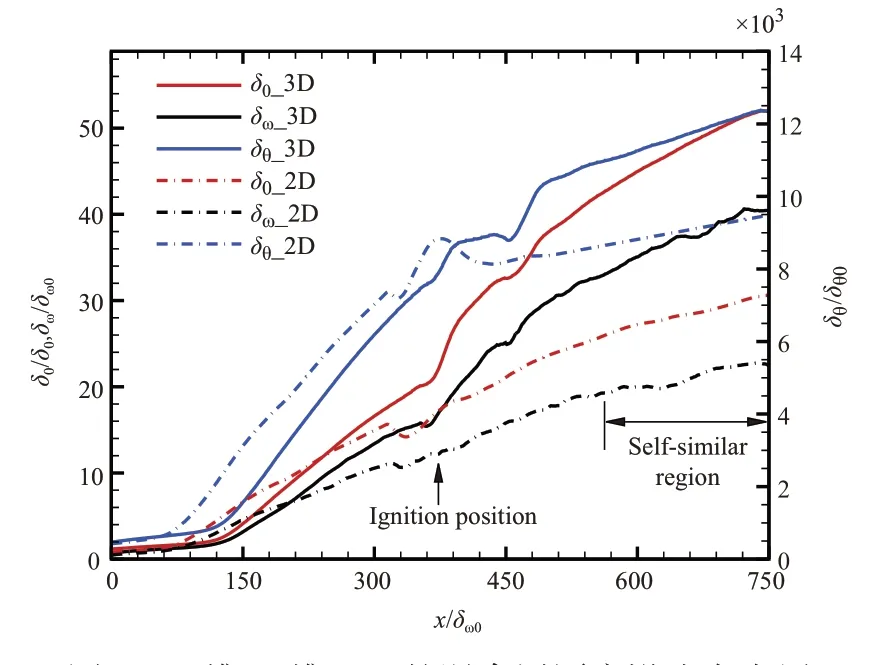
图7 二维/三维LES的混合层厚度沿流向发展Fig.7 Thickness development of mixing layer flows for 2D/3D LES

图8 超声速湍流燃烧混合层流动自相似区判定Fig.8 Determination of self-similar regions for the mixing layer flows

表2 二维/三维大涡模拟下混合层增长率Table 2 Mixing layer thickness growth rate for 2D/3D LES

2.5 速度型、雷诺应力和湍动能

对自相似段几个不同流向站位分布做算术平均后，图9给出了二维/三维LES和DNS[33-34]的自相似段湍流统计相关量的分布特征。由图9可见，三维LES的速度型、湍动能及雷诺剪切应力均与DNS 结果相当。二维/三维LES 的无量纲流向速度分布基本相符。然而，相较于三维LES结果，二维LES 的湍动能峰值增大了约59%，而雷诺剪切应力峰值减小了约62%。此外，二维LES 的湍动能和雷诺剪切应力在法向的扩散更加强烈，导致其分布更加宽阔。Liou等[35]的无反应可压缩二维LES下的混合层流动的湍动能和雷诺剪切应力同样呈现当前结果的分布特征。

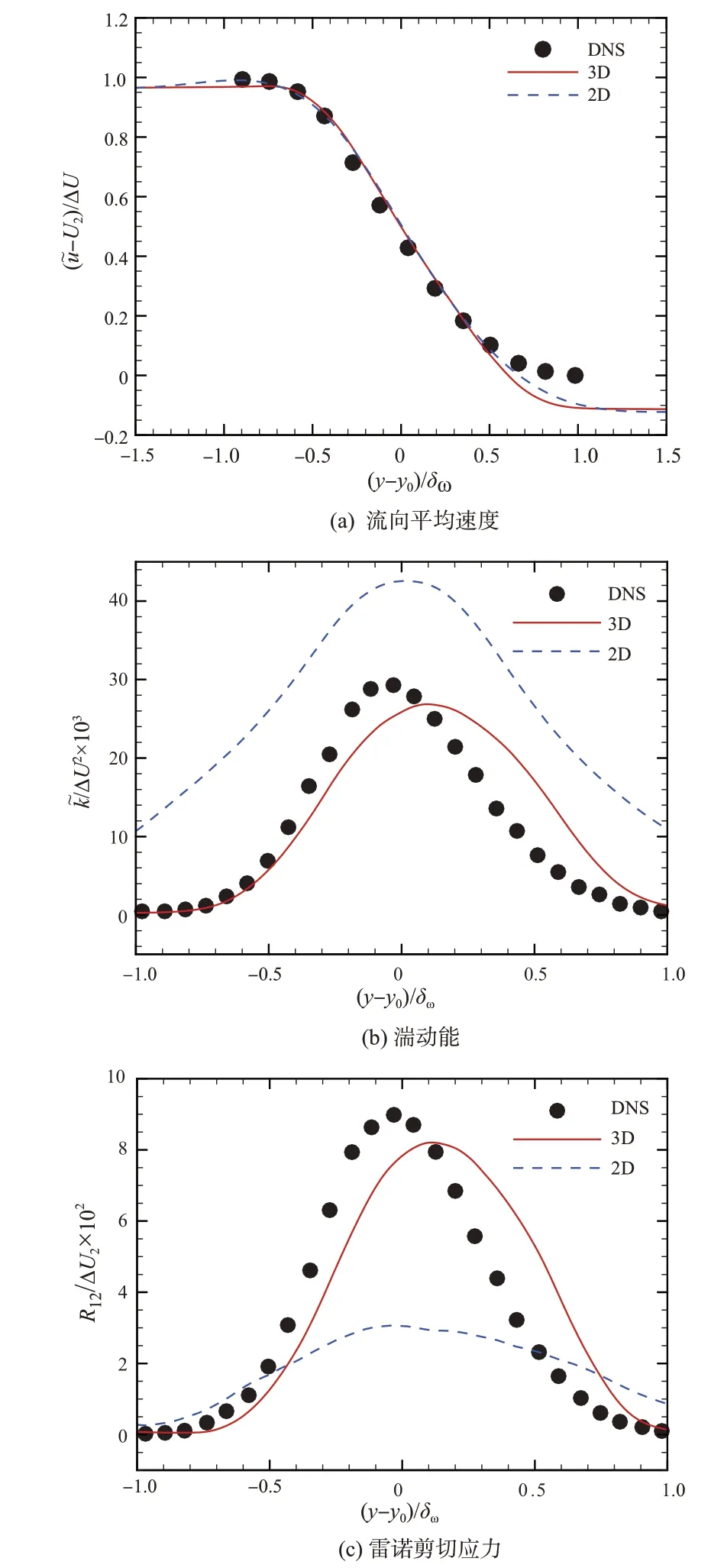
图9 二维/三维LES的统计平均速度型、湍动能和雷诺剪切应力对比Fig.9 Mean profiles of streamwise velocity,turbulent kinetic energy and Reynolds shear stress for 2D/3D LES compared to DNS results

2.6 湍流能谱

图10对比了二维/三维LES的能谱。其中，斯特劳哈尔（Strouhal）数定义为：Sr=f·δθ0/Uc，δθ0表示入口边界层厚度，而Uc= (U1+U2)/2，E(k) = 0.5[E(u) + E(v) + E(w)]。在图10（b）中，为清晰起见，将E(v2)除去了因子102。观测点位于混合层中心位置x=0.83Lx，y*=(y-yc)/δω=-0.46（三维），-0.17（二维）。由图10可见，二维和三维情况下的能谱均具备宽阔的频域范围，表明流动达到充分发展湍流状态。此外，二维/三维LES 计算获得的在含能和耗散尺度之间的区间能谱斜率均满足-5/3律。然而，由图10（b）的法向速度v的能谱可知，二维LES 计算获得的法向速度在各个尺度上的脉动相较于三维LES结果都更加强烈。

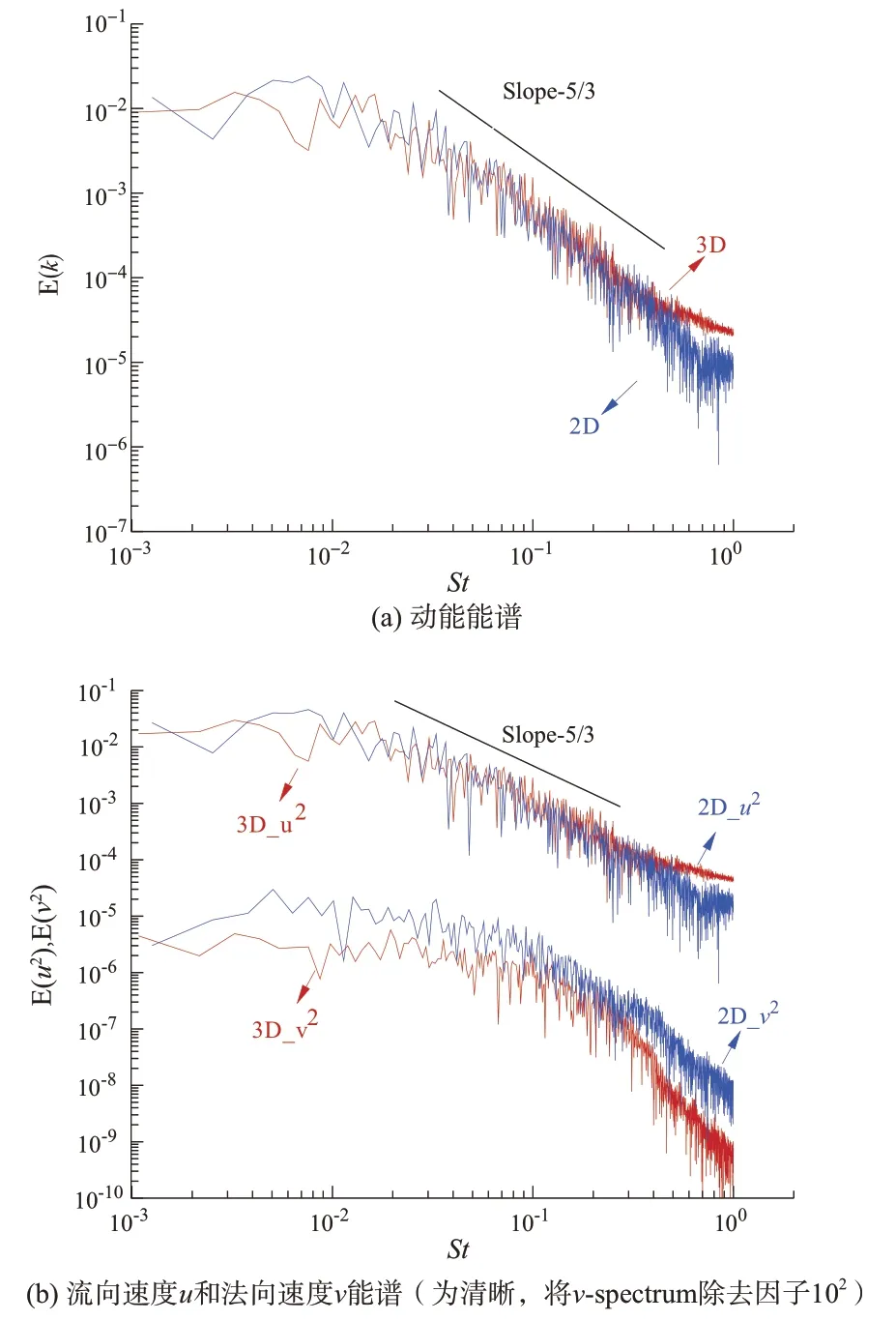
图10 二维/三维LES的能谱对比Fig.10 Energy spectrum for 2D/3D LES

2.7 统计平均温度及其脉动

图11 对比了二维/三维LES 所给出的统计平均温度云图和计算域流向出口温度分布。由图11（a）、图11（b）可见，三维LES计算所得火焰温度明显高于二维LES结果。截取计算域出口温度分布得到图11（c）：三维LES计算域出口处温度峰值达到2.74T0(2040K)，而二维LES 的峰值仅为1.99T0(1480K)，比前者减小了27%。以上结果表明，二维LES所预测的统计平均温度被严重低估。

图12给出了二维/三维LES计算得到的温度脉动结果，其中图12（c）给出了温度脉动峰值及峰值所在法向位置沿流向的分布。由图12（a）、图12（b）可见，二维计算得到的温度脉动均方根峰值明显高于其对应的三维结果。二维/三维LES 均呈现点火导致最大温度脉动，如图12（c）所示的结果。但点火后，二维/三维LES的所取得的峰值呈现截然相反的对称性：前者趋于燃料一侧（即yTrms/δω0>0），而后者趋于氧化剂一侧（即yTrms/δω0＜0）。

图12 二/三维LES的温度脉动结果Fig.12 Statistical temperature fluctuation for 2D/3D LES

正如2.3节所揭示的，二维LES的湍流旋涡运动中的涡拉伸、压缩机制失效，导致二维LES的旋涡结构与三维LES显著不同，燃料和氧化剂相遇的火焰前锋接触面面积从而存在差别，进而致使二维LES难以获得准确的燃料消耗率/燃烧效率，最终导致图11所示的二维LES的统计平均火焰温度显著低于三维LES结果。

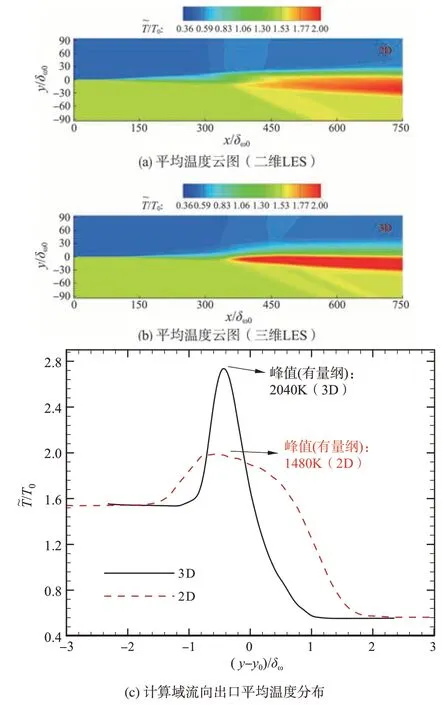
图11 二维/三维LES的统计平均温度Fig.11 Mean temperature for 2D/3D LES

3 结论

本文通过对对流马赫数为0.61的超声速湍流燃烧混合层流动开展二维/三维大涡模拟，探讨了三维效应对于超声速湍流燃烧流动LES的重要性。研究表明：

（1）相较于三维LES，二维LES下的超声速湍流燃烧混合层的增长率大幅减小，其中动量厚度减小幅度约为23%。二维LES的无量纲速度型与三维LES结果一致，雷诺剪切应力明显偏小，峰值减小约62%；湍动能明显偏大，峰值增大约59%。此外，雷诺剪切应力和湍动能的扩散明显增强，导致其分布宽度增加。此外，二维LES 计算所得的湍动能能谱与三维LES 结果相似，在含能涡区域均满足-5/3分布律。

（2）由于二维流动中漩涡拉伸、压缩机制失效，致使二维LES计算所得的湍流流动结构与三维LES存在显著差别：二维LES中湍流呈现清晰的旋涡生成、发展、并对和破碎演化规律，而三维LES的湍流结构呈不规则状。由于湍流和燃烧的相互作用，二维/三维的燃烧场（包括混合分数场、温度场等）也存在显著差别。旋涡运动对燃料和氧化剂进行掺混，掺混界面为火焰前锋面。由于二维/三维流场的旋涡结构不同，致使火焰前锋面面积不同，导致二维LES 计算获得的统计平均火焰温度显著低于三维LES 结果。在本算例中，计算域出口处的二维LES 的火焰温度峰值比三维LES 结果低约27%。此外，二维LES的温度脉动显著高于三维LES结果。

综上所述，三维效应对于LES 准确模拟超声速湍流燃烧流动至关重要。