一种基于混合MCMC的时域波达方向估计算法*

李国彬，宋晓鸥，钮嘉铭

(武警工程大学 a.研究生大队；b.信息工程学院，西安 710086)

0 引 言

对于宽带阵列信号波达方向的估计，一般都是通过构建宽带信号的频域模型，将问题转换到频域进行处理，例如ISM类算法[1-2]和CSM类算法[3],但这两类算法在运行的过程中都会引入转换误差，运算复杂度十分高，同时在处理一些宽带和窄带同时存在的混合信号上的表现也欠佳。如何估计宽带和窄带并存的复杂信号，降低模型的估计误差，是目前波达方向估计的主要研究方向。2005年，William等人[4]提出了一种宽带、窄带同时适用的的时域信号模型，为波达方向估计提供了新的思路，但是该方法是基于低通信号重构理论下建立的模型，对于信号的采样频率要求较高，工程上难以实现。2011年，赵拥军等人[5]在此模型的基础上进行了改进，提出了一种以带通信号重构理论为基础的阵列信号处理时域模型，有效地降低了采样频率，同时对模型的适用性也进行了改进。这两种波达方向估计的时域模型都是通过建立关于未知参数的贝叶斯后验分布函数来进行参数的估计，因此贝叶斯后验分布函数的求解精度直接影响着参数估计的性能，而时域模型的后验分布函数是复杂的，在求解的过程中必然会遇到多维积分的计算，这极大地增大了求解的难度。采用最大似然法进行多维搜索虽然可以近似地求解出贝叶斯后验分布函数的极大值，但这显然是复杂的，不仅运算量大而且求解的精度也难以满足实际的需求。

近年来，由于马尔科夫链蒙特卡洛(Markov Chain Monte Carlo,MCMC)方法在统计物理学上的出色表现，引起了越来越多通信学者的注意，因此也被应用到信号的参数估计上来[6-8]。MCMC方法可以产生一个平稳分布为任意函数的马尔科夫链，基于这一点可以将MCMC方法运用到贝叶斯后验分布函数的求解上来，提高贝叶斯函数求解的效率和精度。但是马尔科夫链的构造过程并不是简单的，马尔科夫链的初始状态以及提议函数的选择都会影响马尔科夫链的收敛速度速度和收敛效果。考虑到这一点，本文主要对MCMC方法中马尔科夫链的构造过程进行了改进：采用多链并行的方式进行马尔科夫链的构造，将原本的长链划分为多个短链，并且就此模型对状态空间进行了优化；在生成马尔可夫链的过程中，基于交叉的原则动态地选择提议函数，且每条短链采用不同的交叉原则；由提议函数生成候选状态的过程采用单元素和多元素混合移动的方式。

1 时域信号模型及贝叶斯后验分布函数

为了便于分析，选择阵列结构较为简单的M元均匀直线阵作为信号的接收阵列。假设有K个信号源从远场入射，第k个信号源的频率范围为fk∈[fk1,fk2],其中，k=1,2,…,K,fk2=fk1+Bk,fk1和fk2分别代表上限频率和下限频率,Bk为信号带宽,信号源的入射角度θ和阵元间的延迟τ可以表示为

θ=[θ1,θ2,…,θK]T,

(1)

τ=[τ1,τ2,…,τK]T。

(2)

式中：

(3)

式中：d表示均匀直线阵的阵元间距，c表示光传播速度。

根据带通信号的重构定理，第k个信号源发射的信号sk(t)可以表示为

(4)

(5)

式中：ψ(t)为重构函数,[-L,L]为实际进行重构的区间。为了保证重构信号不混叠，采样周期Ts满足[9]

(6)

由式(4)便可表示出第m个阵元接收到第k个信号为

(7)

定义

hl(t)=ψ(lTs-t)ω(lTs-t)，

(8)

ω(l-t)为窗函数(这里选择海明窗)，可以降低由于取近似值带来的误差。

对式(7)进行时域离散采样，并用n-l代替l可得

(9)

式中：sk(n-mτk)≜sk(nTs-mτk)，hl(mτk)≜ψ(lTs-mτk)ω(lTs-mτk)。则阵元m接收到的信号为

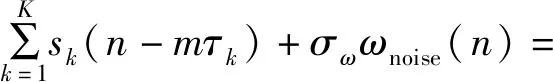
m=0，1，…，M-1。

(10)

式中：σω表示噪声的方差，ωnoise(n)表示均值为0、方差为1的高斯白噪声。

天线阵的总输出y(n)=[y0(n),y1(n),…,yM-1(n)]T可表示为

(11)

式中：

(12)

a(n)=[s1(n),s2(n),…,sk(n)]T。

(13)

阵列接收信号的时域模型为

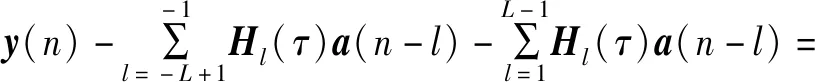
H0(τ)a(n)+σωωnoise(n)。

(14)

利用贝叶斯准则来估计波达方向的核心就是建立关于未知参数的后验分布函数。式(14)共有τ、K、σω、a(n)四个位置参数，分别代表信号延时、信源个数、噪声参数、信号矢量，本文只考虑在信号源个数已知情况下的信号时延的估计，基于阵列接收信号的时域模型，结合未知参数的先验分布，通过积分的方式消除无关参数，得到关于信号时延的贝叶斯后验概率函数[4]：

(15)

式中：γ0和ν0为超参数，一般设置为0；N为快拍数；δ为与信噪比有关的参数；

(16)

(17)

π(τ|Z)便是关于信号时延的贝叶斯后验分布函数，如果能求解出其最大值，那么便可以得到基于样本统计量的信号延时的最佳估计，但这显然不是容易的：关于信号延时的贝叶斯后验概率密度函数是一个多峰值函数，利用谱峰搜索技术求解最大值势必会带来庞大的计算量，求解的精度也会受限于搜索步长。

2 基于混合MCMC的时域波达方向估计算法

MCMC方法最关键的就是转移核的构造，选取的转移核应当使得构造的马尔科夫链满足细节平稳。Metropolis-Hastings(M-H)抽样法是MCMC中常用的一种方法，通过选取合适的提议函数来抽取样本，并以一定的的概率选择是否接受候选状态，直到样本最后收敛。

图1为M-H抽样法产生的马尔科夫链的流程图，初始状态和提议函数相当于M-H抽样法的输入，初始状态的不同会导致马尔科夫链达到平稳所需要的时间不同，提议函数的选择则直接关系到抽样结果，选择遍历性不同的的提议函数会产生不同的收敛速率和结果。因此，我们考虑从初始状态和提议函数入手来提高马尔科夫链的收敛效果和速率。

图1 M-H方法的流程图

2.1 并行马尔科夫链

以信源个数等于3的情况为例，结合式(3)我们可得出需要构造的马尔科夫链的状态空间为一个“正方体”，在整个“正方体”中进行马尔科夫链样本的选择不仅需要的时间长，而且很难确保在有限迭代次数下构造的马尔科夫链能够收敛。初始状态的选择不当也可能造成马尔科夫链未能收敛，虽然可以通过预估计的方式对初始状态进行修正，但这显然是复杂的，对估计的实时性也会造成影响。考虑到以上的因素，我们将马尔科夫链的构造过程拆分成多个并行的短链来进行，也就是说将状态空间划分为多个子空间如图2所示，在每个子空间分别进行马尔可夫链的构造，构造过程中的初始状态是由每个子空间决定的，最后将每个子空间的结果进行合并形成最终的马尔科夫链。这种并行构造方式极大地改善了初始状态选择不佳对马尔科夫链收敛速度和结果的影响，在相同的迭代次数下马尔科夫链也更容易达到收敛状态。

图2 并行构造方式的状态空间

基于此类模型，我们还发现贝叶斯后验概率函数对于状态空间的选择是“无序”的。例如，实际时延值为[τ1,τ2,τ3]，而状态空间中的其他“有序”状态[τ1,τ3,τ2]、[τ2,τ1,τ3]、[τ2,τ3,τ1]等，与实际时延[τ1,τ2,τ3]有着相同的贝叶斯后验概率函数值，这对马尔科夫链的构造是非常不利的，严重影响了算法的收敛速率。因此，我们采用图3的方法对状态空间进行了优化和改进，可以看出改进后的状态空间相比于之前明显减少，但是又包含了所有的“无序”状态。事实上，经过改进后的状态空间依然存在部分“有序”状态，但去除这部分“有序”状态会使算法的复杂度骤升，因此我们选择保留这部分“有序”状态，并且少量的“有序”状态对于算法的收敛速度和收敛结果也有一定的提升。

图3 改进的状态空间图

2.2 混合MCMC方法

选择遍历性强弱不同的提议函数对马尔科夫链的收敛速度和结果影响十分大，遍历性弱的提议函数会导致算法收敛速度慢，遍历性强的提议函数又可能会出现近似收敛的情况。考虑到这点，这里采用一种混合的提议函数选取方式：在生成马尔科夫链的过程中，随机交叉地使用遍历性弱的随机游走采样(下一次的采样结果是当前状态的随机扰动)和遍历性强的独立游走采样(下一次的采样结果是独立的，与当前状态无关)。这种混合的采样方式相比于随机游走采样收敛速度更快，相比于独立游走采样收敛结果更加稳定。从图4可以看出，由提议函数生成候选状态的过程中，提议函数的选择是随机多变的，包含了遍历性强弱不同的提议函数。

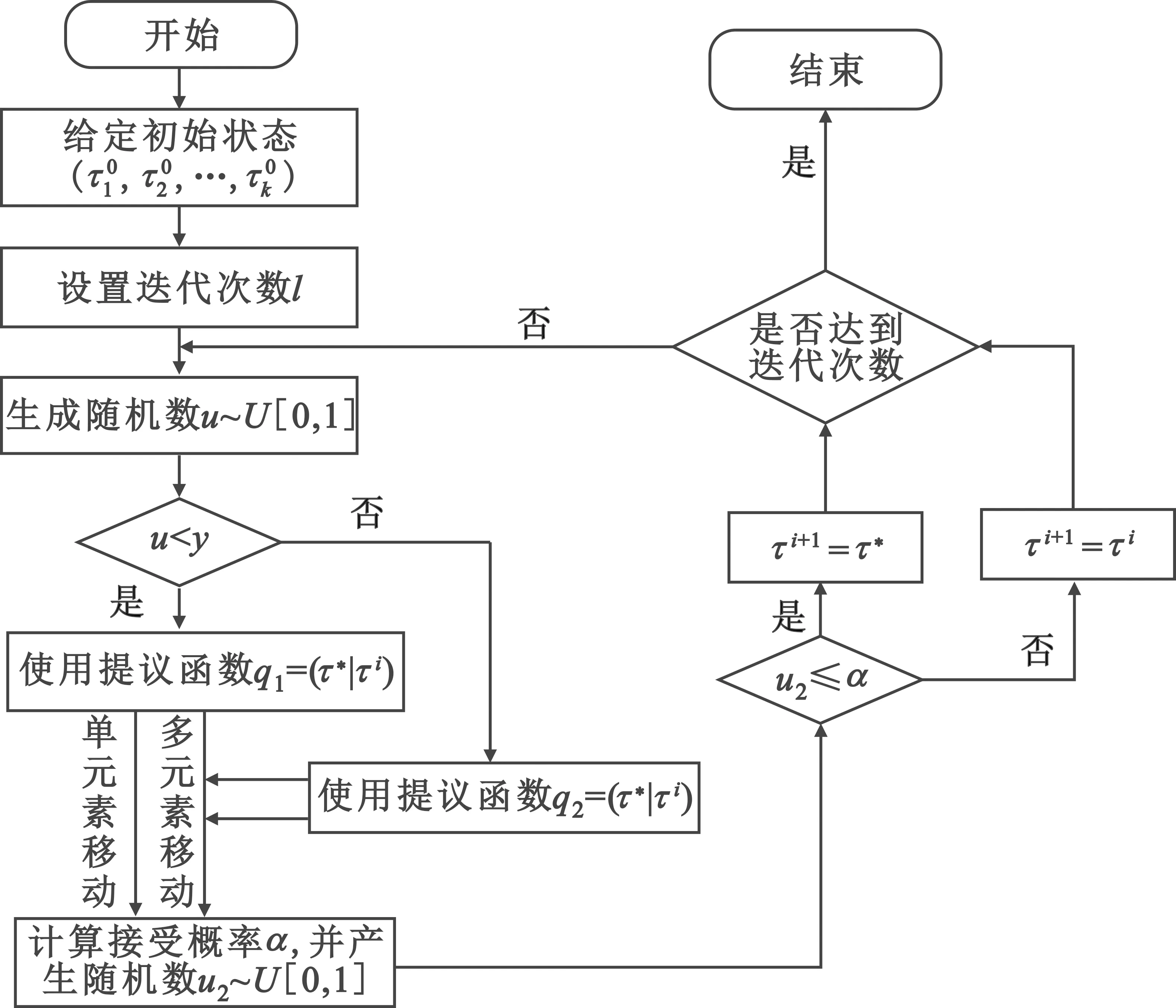
图4 混合MCMC的算法流程图

同时此模型下的候选状态是一个多维向量，每个维度的值对该状态都有贡献，如果我们同时生成多维度的候选状态，就很容易把一些单维度性能较好的状态给拒绝，而单元素移动每次只改变一个维度的值，这样就会将收敛性较好的维度传递下去，从而加快收敛速度和改善收敛结果[10]。改进后的算法采用多元素和单元素混合移动的办法来生成候选状态，如图4，在马尔科夫链未达到收敛状态前采用多元素移动的方式来生成候选状态，加速状态的游离，在马尔科夫链接近收敛状态后(一般根据经验来决定)采用单元素。

3 仿真与分析

实验采用阵元数目M=12的均匀直线阵，阵元间距为波长的一半，时域模型中的插值个数2L-1=11，信号源的个数K=3(其中两个为窄带调幅信号，一个为宽带线性调频信号,信号的强度比为2∶3∶4)，信号源的方向分别为10°、15°、20°。采样的快拍数为128，仿真环境中的信噪比为10 dB，马尔科夫链的迭代总次数为2 000次。

图5给出了采用单链构造方式的估计结果，可以看出马尔科夫链需要大约1 800次的迭代样本才能够收敛。图6给出了采用多链并行方式的估计结果，可见在实际波达方向对应的子空间2内，只需要450次左右迭代样本便可以收敛。事实上采用并行的方式可以在相同的时间完成多个(短)链的构造，因此算法的实时性并不会降低，算法的收敛结果反而会更加精确。并且我们可以看出，虽然实际的波达方向并不其余在子空间内，但是其他子空间构造的马尔科夫链仍然有部分正确结果，也就是说单维度的收敛性也能够传递下来，这就为单元素移动提供了一定的理论依据。

图5 MCMC方法的估计结果

图6 多链并行方式下的估计结果

采用混合MCMC的方式构造马尔科夫链，在1 800次迭代后样本便可达到收敛。作为对比，图7给出了采用遍历性强的独立游走采样的估计结果，可以看出经过2 000次迭代后，样本达到了一种“伪收敛”的状态，这对于波达方向的估计来讲是非常不利的。

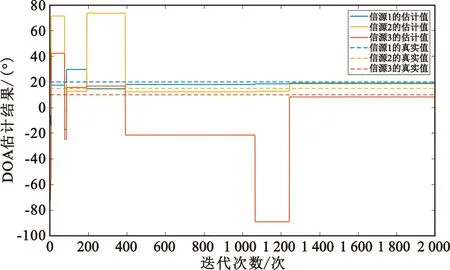
图7 独立游走采样的估计结果

图8给出了在迭代次数末端分别使用单元素移动和多元素移动的DOA估计结果，可以看出，在马尔科夫链达到收敛状态后单元素移动的估计结果在真实值附近波动的幅度更小，这也是为什么在马尔科夫链的末端使用单元素移动的原因。

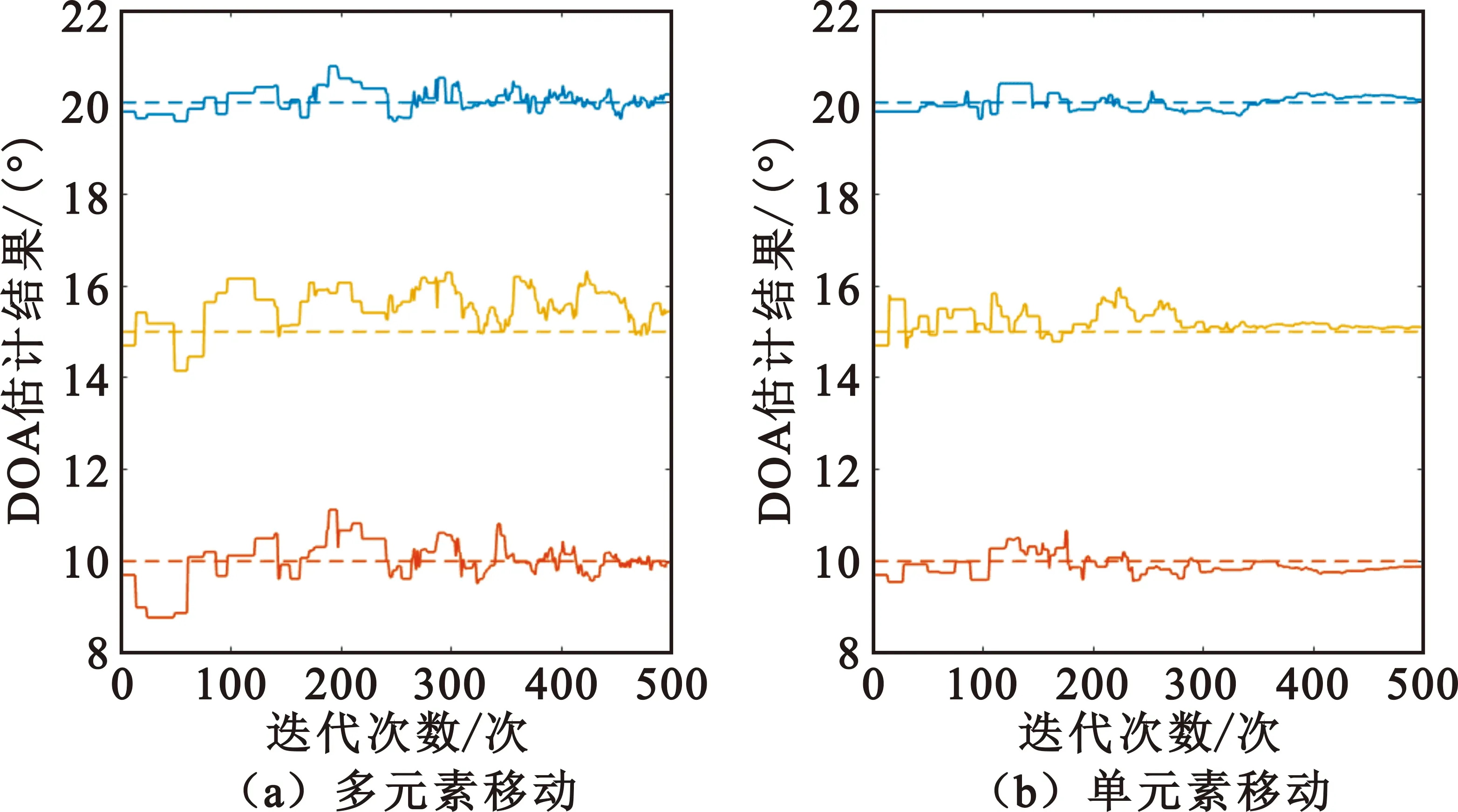
图8 使用多元素移动和单元素移动的DOA估计结果

表1给出了1 000次蒙特卡洛实验中单元素移动和多元素移动的估计结果和均方误差(Mean Squared Error，MSE)[11],可以看出单元素移动的方式极大地改善了MCMC方法的估计精确度。

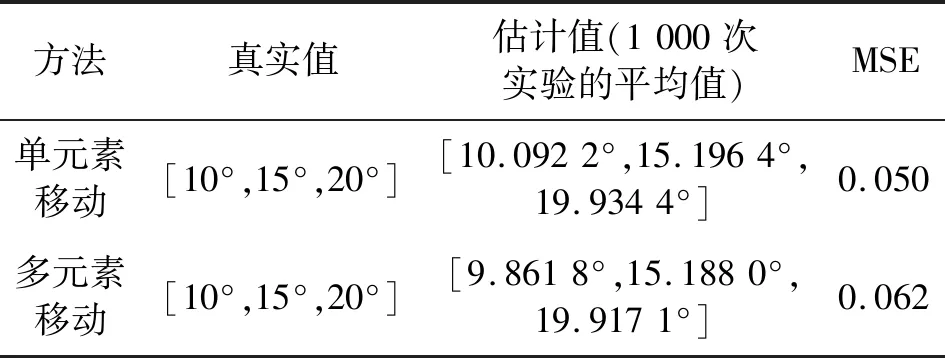
表1 估计结果和误差

(18)

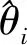
图9给出了不同信噪下和快拍数下本文算法与文献[5]算法和MUSIC算法DOA估计结果的均方误差，可以看出当快拍数固定为128时，MUSIC算法在信噪比较低的情况下表现出极差的性能，而文献[5]算法和改进的并行混合算法在不同信噪比下都表现出较好性能，估计的均方误差远小于MUSIC算法，同时改进后的并行算法相比于文献[5]算法的估计性能又有了一定的提升；当信噪比固定为10 dB时，MUSIC算法的估计性能随快拍数的增加并没有发生明显的变化，而文献[5]算法和改进的并行混合算法都发生了明显的变化，这与其算法的本质有关(文献[5]算法和本文的算法本质上都是利用了贝叶斯原理求解，MUSIC算法则是利用信号与噪声的相关特性)，并且改进的并行混合算法的估计性能要略好于文献[5]算法。

4 结束语

通过构造马尔科夫链的方法可以实现高分辨率的波达方向估计，但是马尔科夫链对初始状态、提议函数等有很高的要求，因此本文采用了一种并行混合的方式进行构造。通过实验仿真可知，本文的模型可同时适用于宽带和窄带信号的波达方向估计；在相同的迭代次数下，本文的并行混合构造方式相比于文献[5]算法表现出更好的收敛稳定性，估计的精度也要高于传统的MUSIC算法和文献[5]的算法；同时，本文采用的并行运算方式很大程度上减少了算法的运算时间，提高了估计的实时性。此算法可用于复杂信号的高分辨率波达方向估计，估计的精度和实时性都能满足实际需求。

下一步工作将研究基于波达方向估计的自适应抗干扰技术，将此算法的估计结果与自适应抗干扰技术相结合，提高系统的抗干扰能力。