基于深度神经网络的自适应波束形成算法*
任燕飞,杜 盈,张劲东
(1.中国西南电子技术研究所,成都 610036;南京航空航天大学 电子信息工程学院,南京 211106)
0 引 言
波束形成技术是阵列信号处理的重要分支,在雷达、声呐、通信和电子对抗等领域有着广泛的应用。基于最大信噪比(Signal-to-Noise Ratio,SNR)准则、最小均方误差(Minimum Mean Squared Error,MMSE)准则以及最小方差无失真响应(Minimum Variance Distortionless Response,MVDR)准则等波束形成方法,在期望信号或干扰信号角度发生变化时要重新计算权矢量,计算量大,难以满足实时更新最优权矢量的要求。随着人工智能和神经网络技术的快速发展,将神经网络方法应用于波束形成技术当中,利用神经网络对数据进行预训练,然后在泛化阶段用训练后获得的网络模型自适应地输出权矢量,当入射信号到达角(Angle of Arrival,AoA)发生变化时,相对于传统的波束形成算法要经过大量的计算,神经网络在泛化阶段的响应时间是很短的,阵列天线就可以利用神经网络快速进行波束形成。
目前已有很多基于神经网络的波束形成技术研究。文献[1-3]分别采用Hopfield网络、主元分析网络和多层感知机进行波束形成,但这些方法并没有充分利用神经网络的非线性拟合能力。文献[4-5]使用径向基函数(Radial-basis Function,RBF)网络拟合接收信号协方差矩阵和权矢量的映射关系进行波束形成,但需要进行聚类操作来获取基函数中心,神经网络训练过程比较复杂,且RBF网络是单隐层的前馈型网络,在训练样本增加时隐层神经元数量大大增加,网络结构过于庞大。为克服RBF网络的缺陷,深度神经网络(Deep Neural Network,DNN)技术开始被用于波束形成中。柏沫羽等人[6]设计一个三层隐层的深度神经网络,避免了RBF网络的聚类操作,可在大回波数据下快速进行波束形成,但引入了对同一入射信号组合权矢量的相似性约束,且受限于样本设置的6个固定角度的干扰场景。Ramezanpour等人[7]利用卷积神经网络(Convolutional Neural Network,CNN)替代高复杂度的优化算法,通过输入接收信号的自相关矩阵来预测近似的最优权重矢量,但该方法为了较好的拟合效果和更为简单的网络结构,需要进行繁琐的数据预处理步骤,引入了过多角度的先验性假设。此外,文献[8-10]设计了基于DNN、CNN和生成对抗网络(Generative Adversarial Network,GAN)等网络架构的波束形成器快速产生高品质的超声波图像;Liu等人[11]基于长短时记忆(Long Short-Term Memory,LSTM)的时间相关性设计一个LSTM循环神经网络(LSTM-based Recurrent Neural Network,LRNet)实现无人机通信中的波束对准;Dong等人[12]提出一种DNN的稳健波束形成方法实现无线通信中较高的保密率和灵活的波束导向:但这些基于深度神经网络架构的波束形成算法对于空域抗干扰并不适用。
本文基于现有研究和存在的问题提出了一种新的算法——深度神经网络的自适应波束形成(Deep Neural Network Adaptive Beamforming,DNNABF)算法,随机的期望信号和干扰信号AOA组成的向量作为DNN的输入,MVDR算法权矢量作为输出,采用4层隐藏层并用PReLU函数激活,输出层用 tanh函数激活,Adam算法作为优化器,使网络具有较好的泛化性能,在入射信号到达角度改变时,分别在期望信号和干扰信号角度上自适应地形成波束和零陷,实时进行空域抗干扰,可应对更加复杂的干扰场景。
1 信号模型
本文考虑一个阵元数为M的均匀线阵,阵元间距d,有K+1个入射信号,期望信号到达角度为θ0,第k个干扰信号到达角度为θk(k=1,2,…,K),入射信号AOA组成的向量θ=[θ0,θ1,…,θK]。天线阵列的接收向量为
X(t)=AS(t)+n(t) 。
(1)
式中:X(t)=[x1(t),x2(t),…,xM(t)]T;A为阵列流形;S(t)=[s0(t),s1(t),…,sK(t)]T为期望信号复包络,sk(t)为第k个干扰信号的复包络;n(t)为噪声。
设p=[0,1,…,M-1]T,那么阵列流形A可表示为
A=ej2π/λdpsin θ=
(2)
Capon于1969年提出了MVDR波束形成器,它使干扰和噪声贡献的功率最小,同时保持感兴趣方向上的信号功率不变[13]。该问题可描述为
(3a)
s.t.wHa(θ0)=1 。
(3b)
通过拉格朗日乘子法可求得权矢量wMVDR为
(4)
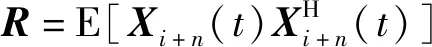
(5)
由此可计算阵列响应为
(6)
方向图增益为
(7)
2 面向波束形成的深度神经网络设计
2.1 深度神经网络设计
2.1.1 激活函数的选择
sigmoid函数是深度学习领域使用频率最高的激活函数,但容易产生梯度消失,模型收敛速度慢,而且在前向传播时运算比较耗时。tanh函数也是一种常见的激活函数,模型收敛速度更快,但也容易出现梯度消失,且幂运算耗时。
深度神经网络中最常用的是ReLU激活函数,可解决梯度消失的问题,计算速度快,收敛速度比sigmoid函数和tanh函数快得多。若输入为x,那么ReLU激活函数可表示为
(8)
但当x<0时梯度为0,负的梯度在这个ReLU被置零,这个神经元可能再也不会被任何数据激活,神经元坏死。为解决这个问题,可选择 PReLU激活函数。PReLU激活函数可用式(9)表示,其中负值部分的斜率α是根据数据来定的,而非预先定义的。
(9)
隐藏层的激活函数可选用PReLU激活函数,而在回归问题中,输出层一般采用线性函数激活,网络输出可以回归到任意值。由于权系数的实部和虚部值都处于[-1,1]区间内,所以本文的输出层采用tanh函数激活,使网络输出回归到[-1,1]内的值。tanh激活函数可用下式表示:
(10)
2.1.2 优化算法选择
随机梯度下降(Stochastic Gradient Descent,SGD)及其变种很可能是应用最多的优化算法。SGD算法的学习率是固定的,其学习过程有时会很慢。动量(Momentum)方法通过添加动量来加速学习,但引入了新的超参数。自适应学习率算法可适应模型参数各自的学习率,具有更快的收敛速度,适合训练更深更复杂的神经网络。AdaGrad(Adaptive Gradient)算法可以独立地适应所有模型参数的学习率,针对参数自适应调整学习率。RMSProp(Root Mean Square Prop)算法对AdaGrad算法进行改进,在非凸设定下效果更好,改变梯度积累为指数加权的移动平均。Adam(Adaptive Moment Estimation)算法即自适应时刻估计方法,可看作动量法和RMSProp的结合,不但使用动量作为参数更新方向,还能够自适应调整学习率。整体来说,Adam是最好的选择[14]。而且实践表明,Adam优化器可以高效地解决局部深度学习问题,效果优于其他随机优化算法[15]。
(11)
(12)
参数的更新公式为
(13)
一般β1设为0.9,β2设为0.999 9,ε设为10-8。与其他自适应学习率算法相比,Adam算法收敛速度快、学习效果好,可解决其他优化算法学习率消失、收敛慢以及高方差参数更新导致损失函数波动较大的问题,优化了模型性能。
2.1.3 网络深度设计
Hornik等人[14]已经证明,一个前馈神经网络只需具备单层隐含层和有限个神经单元,就能以任意精度拟合任意复杂度的函数。但张强等人[15]在研究中发现,隐藏层层数越多网络泛化能力越强,拟合效果越好,不过网络复杂度提高,训练时间增加。当然浅层网络的泛化能力和拟合效果可以通过增加网络宽度即隐藏层节点数来弥补,但是Bengio等人[16]已经得出结论——网络深度减少一层,用来拟合函数的计算元素可能要呈指数增长,增加网络深度比增加宽度更有效。因此为了提高网络训练效率,应该使用深度网络,并选择网络的拟合效果达到要求时较少的隐藏层数。
天线方向图最能直观地反映出用网络拟合的权矢量来形成波束和抑制干扰的效果。本文以MVDR算法为基准,采用试错法确定网络深度,隐藏层数量从2层开始,逐渐增加。当期望信号到达角度为3°、4个干扰信号到达角度分别为-28°、-17°、22°和39°时,选择2层(节点个数分别为2 048、1 024)、3层(节点个数分别为2 048、1 024、1 024)和4层(节点个数分别为2 048、1 024、1 024、1 024)隐藏层得到的天线方向图如图1所示。
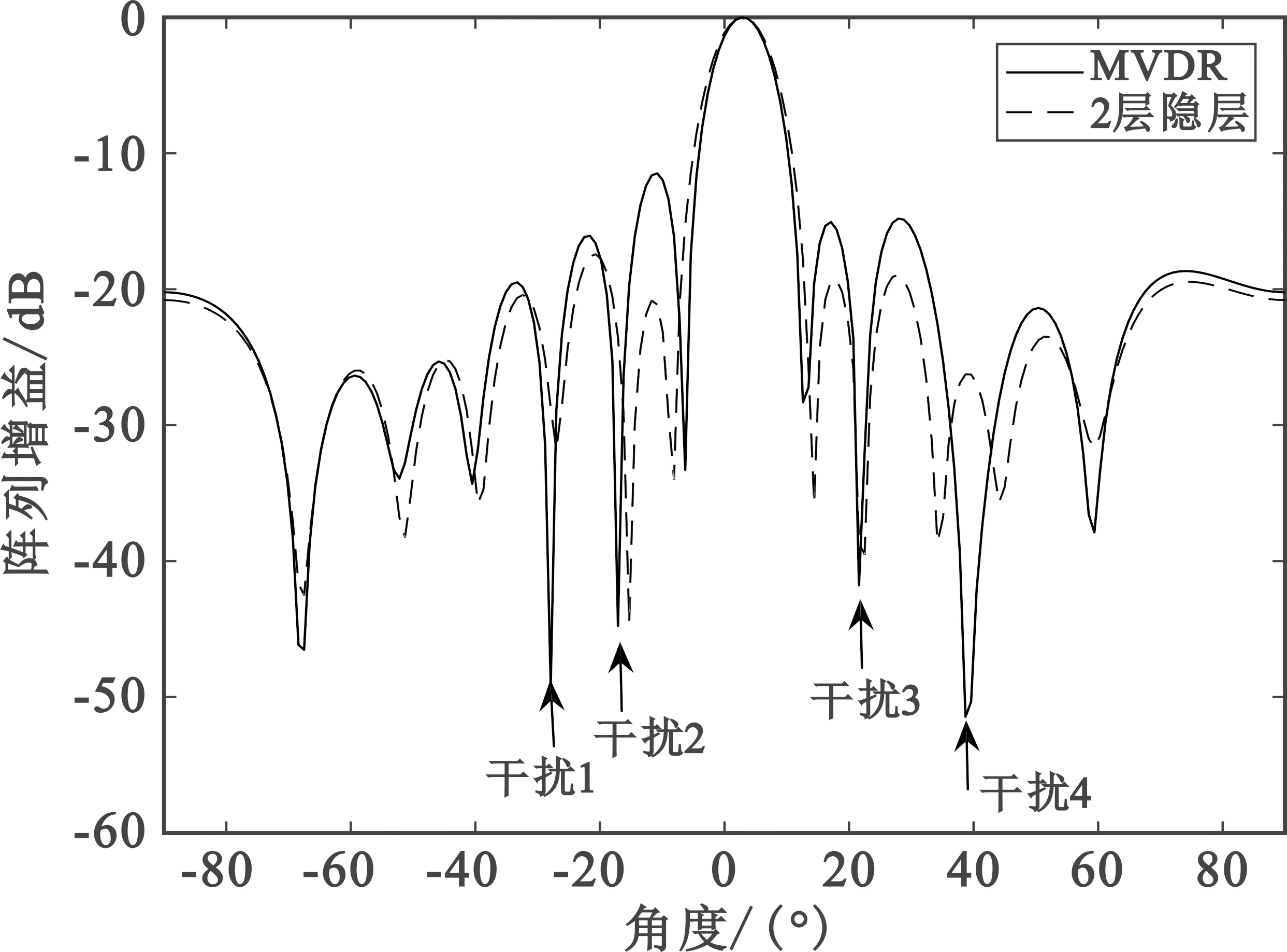
(a)2层隐层
从图1可以看到,2层和3层隐藏层的网络在主波束相对MVDR均有偏移,在39°方向上均没有很好地形成零陷,而4层隐层的网络主波束与MVDR算法几乎完全贴合,且在各个干扰角度上都形成了较深的零陷,达到了抑制干扰的目的。4层隐层的网络可达到较好的波束形成效果,因此本文的DNN包含4层隐藏层。
2.2 基于DNN的ABF算法
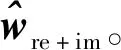
Step1 随机产生L个角度向量θ作为DNN训练样本的输入数据,θtrain∈RL×(K+1)。
Step2 利用式(4)求得MVDR算法权矢量,从而获得wre+im。
Step3 用获得的训练样本{θtrain,wre+im}训练DNN模型。
Step4 用训练好的DNN进行测试,输入新的测试数据θtest网络可自适应地输出权矢量。
Step5 将网络输出转变为复数形式的权矢量wDNN,用wDNN进行波束形成。
设4层隐藏层的节点数分别为d1、d2、d3、d4,本文的DNN结构如图2所示。

图2 DNN训练结构
为了更好地表述DNN中各层的关系,设相邻两层网络之间的连接权值矩阵分别为V1、V2、V3、V4、V5,其维度分别为(K+1)×d1、d1×d2、d2×d3、d3×d4和d4×2M,各层偏置为γ1、γ2、γ3、γ4、γ5,那么每个隐藏层的输出可用式(14)~(17)表示:
h1=σ2(θtrainV1+γ1),
(14)
h2=σ2(h1V2+γ2),
(15)
h3=σ2(h2V3+γ3),
(16)
h4=σ2(h3V4+γ4)。
(17)
网络输出为
(18)

(19)
本文构造的DNN含有4层隐藏层,采用PReLU激活函数激活,解决梯度消失的问题;采用Adam优化算法避免其他优化算法学习率消失、收敛慢以及损失函数波动较大的问题,使网络具有较强的学习能力和较好的泛化性能。当阵列天线接收到的入射信号角度改变时,DNN可自适应地输出相应权矢量,实时形成波束。
3 计算机仿真与性能分析结果
本文在Intel i5-9400HQ CPU、16 GB内存、Matlab2016a、Tensorflow2.0仿真平台下进行仿真,采用均匀线阵,仿真参数设置如表1所示。

表1 仿真参数设置
3.1 本文算法与MVDR算法对比分析
假设有1个期望信号和4个干扰信号以平面波入射,5个入射信号取不同角度并随机赋值。共产生15 100组样本数据,其中15 000组进行训练,100组进行测试。用图2设计的DNN训练100个epoch,4层隐藏层的节点数分为别2 048、1 024、1 024、1 024,而输入层和输出层分别有5个节点和24个节点。
首先比对两种算法的波束方向图。2.1.3中已验证,4层隐层的DNN拟合权矢量进行波束形成,其主波束与MVDR算法很贴近,且在各个干扰角度上都形成零陷,波束形成效果和抗干扰性能较好,本文算法生成的空域抗干扰波形与MVDR算法相近,可以很好地形成波束、对抗干扰。
本文使用实际值与网络预测值的均方误差作为网络的性能度量来评价网络的泛化能力,计算方式如式(19)所示。网络的泛化误差越小,泛化性能越好,让泛化误差尽可能小可降低网络过拟合的风险。以测试误差作为网络的泛化误差,100组测试样本的权矢量拟合均方误差值如图3所示。从图3中可以看出,本文网络的误差值很小,网络具有较好的泛化性能。

图3 测试样本平均误差
下面对比本文算法与MVDR算法的运行时间。根据测试样本的输入角度,统计利用MVDR算法计算权矢量所需时间和DNN拟合权矢量所需时间,各进行20次仿真取平均值,结果如表2所示。相对于传统的MVDR算法,本文方法在运算速度上有将近6.5倍的提升,在入射信号角度改变时可快速进行波束形成,满足实时性要求。

表2 MVDR算法和DNN的计算时间对比
3.2 本文方法与CNN对比分析
下面将本文方法与CNN方法进行对比。CNN前三层为卷积层,第四层为全连接层。设第l层卷积层的卷积核大小为Kl,CNN每层网络输出通道数与DNN对应相等,即三层卷积层卷积核数量分别为d1、d2、d3,而全连接层神经元数量d4=1 024。本文CNN结构和具体参数如表3所示。

表3 CNN模型结构参数
CNN的 padding 设为valid,strides为1,优化器参数与DNN相同,采用3.1节样本,同样训练100个epoch。当期望信号到达角度为18°、4个干扰信号到达角度分别为-32°、-14°、7°和36°时,DNN与CNN方法得到的天线方向图如图4所示,可见DNN与CNN均能够在期望信号角度上形成波束、在干扰信号角度上形成零陷。

图4 DNN、CNN与MVDR天线方向图
为了直观地表现网络拟合权矢量的准确度,将网络输出的权矢量实部和虚部样本对转化为复数形式,并定义两个网络权矢量的相对误差为
(20)
(21)
统计DNN与CNN方法每组测试样本权矢量相对误差值如图5所示。无论是DNN还是CNN拟合权矢量,相对误差都很小,两种网络对权矢量的估计都比较准确。
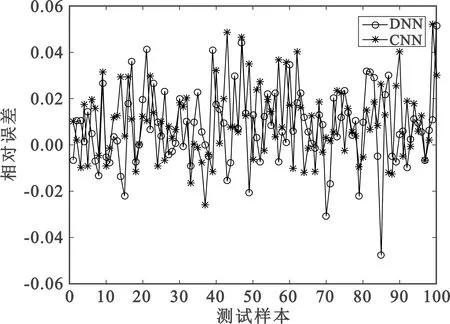
图5 测试样本相对误差
下面分析DNN与CNN算法复杂度。对于CNN,第l层卷积层输出的向量维度Ml=Ml-1-Kl+1,训练整个网络模型的时间复杂度为O(M1K1(K+1)d1+M2K2d1d2+M3K3d2d3+M3d3d4+d4·2M),而训练DNN模型的时间复杂度为O((K+1)d1+d1d2+d2d3+d3d4+d4·2M),在相同网络结构参数下,CNN复杂度要高于DNN。DNN和CNN模型训练时间如表4所示,DNN训练时间远少于CNN。

表4 DNN与CNN训练时长对比
3.3 本文DNN性能稳定性分析
相对3.1中仿真,仅改变干扰源数量,场景1、场景2和场景3分别对应3、4、5个干扰源,网络的输入层节点数依次为4、5、6个,其他参数均不变,各取15 000组训练数据和100组测试数据,网络训练100个epoch,利用网络拟合的权矢量生成的波束方向图,其形成波束位置作为期望信号到达角度的网络估计值,而零陷位置作为干扰信号到达角度的网络估计值,3个场景中各入射信号估计到达角度相对实际到达角度的偏移情况如图6所示。
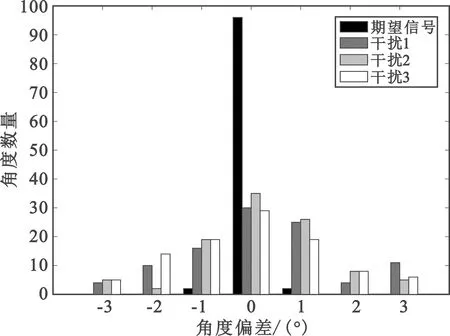
(a)场景1
(22)
(23)


表5 3个场景中的角度偏差和平均误差
由表5可知,干扰源数量改变时网络性能依旧稳定。随着干扰源数量的增加,各个入射信号角度偏差和拟合权矢量的平均误差值略有增加,但3个场景中权矢量的平均误差值都很小,网络具有较好的泛化性能,可以准确地拟合出MVDR算法权矢量。3个场景中各入射信号角度偏差也很小,这说明本文方法可以较为准确地在期望信号方向上形成波束、在干扰信号方向上形成零陷。
4 结束语
自适应波束形成是阵列信号处理的关键技术之一,是实现空域抗干扰的重要方式。阵列天线接收到的信号总是从随机角度入射且快速变化,传统的波束形成算法计算量大,不能实时更新最优权矢量,难以满足实际工程应用需求。本文提出一种DNNABF算法,输入期望信号和干扰信号的到达角度向量,网络输出逼近MVDR算法最优权矢量,同时选用合适的网络深度、激活函数和优化算法使网络具有较好的泛化性能。仿真结果表明,本文方法可准确拟合与MVDR算法相近的权矢量进行自适应波束形成,但其计算速度相对MVDR算法提升了6.5倍,与相同模型结构参数下的CNN相比,DNN的训练时间也远小于CNN,且在不同干扰信号数量的场景中本文设计的DNN都具有稳定的性能。
在本文研究的基础上,未来还可以进一步研究低快拍条件下的DNNABF算法,解决传统算法在低快拍下不够稳健甚至失效的问题。

