弹载俯冲大前斜SAR成像几何校正参数误差影响分析*

陈 娟

(中国西南电子技术研究所，成都 610036)

0 引 言

合成孔径雷达(Synthetic Aperture Radar,SAR)能够全天候、全天时获得高分辨率图像，广泛应用于国民经济、军事及其他对地观测领域[1-3]。将其应用在弹载平台下，利用合成孔径雷达得到的高分辨率图像，通过景象匹配和基于图像的目标识别可大幅提高目标命中精度，因此近年来弹载大前斜SAR成像技术得到了广泛的研究[4-15]。

关于弹载SAR成像几何校正，文献[10]研究了弹载侧视SAR采用RD和CS成像算法及几何校正方法；文献[11]和[12]分别研究了弹载前斜SAR成像中RD、CS和SPECAN成像算法对应的几何校正方法；文献[13]研究了弹载环扫SAR成像算法；文献[14]研究了采用时域BP成像算法带来的图像畸变校正：这些论文分别分析了弹载条件下的不同成像算法及其成像算法带来的形变校正方法，但并未分析实际中由于成像场景环境或各种参数误差带来的问题。如在山地场景中存在高程起伏，SAR图像存在透视收缩、叠掩和阴影等几何畸变现象，SAR图像几何畸变会引起导引头匹配制导误差。关于场景影响的几何校正已有作者开展了详细研究[15]，本文不再赘述。

本文将重点研究弹载俯冲大前斜成像过程中的参数误差对几何畸变的影响。大前斜SAR成像的直接结果为斜距图，与地距图相比形变严重，无法直接用于景象匹配和目标识别，需采用惯导等设备提供的参数进行斜距图转地距图的几何校正转换，因此，几何校正性能和弹道参数精度紧密相关。在末制导阶段俯冲大前斜SAR成像模式下，由于导弹运动速度快，目标多普勒变化剧烈，弹道参数误差对校正结果非常敏感。本文在分析弹载俯冲大前斜SAR成像模式的几何校正方法基础上，分析了弹道参数误差导致的地距图畸变，通过仿真和统计讨论了不同误差情况下的畸变量，为实际系统设计和实现提供了理论参考和应用边界准则。

1 俯冲大前斜SAR图像几何校正算法

1.1 俯冲大前斜SAR斜距图几何失真分析

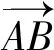
图1 大前斜视SAR几何模型图

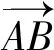
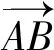
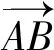
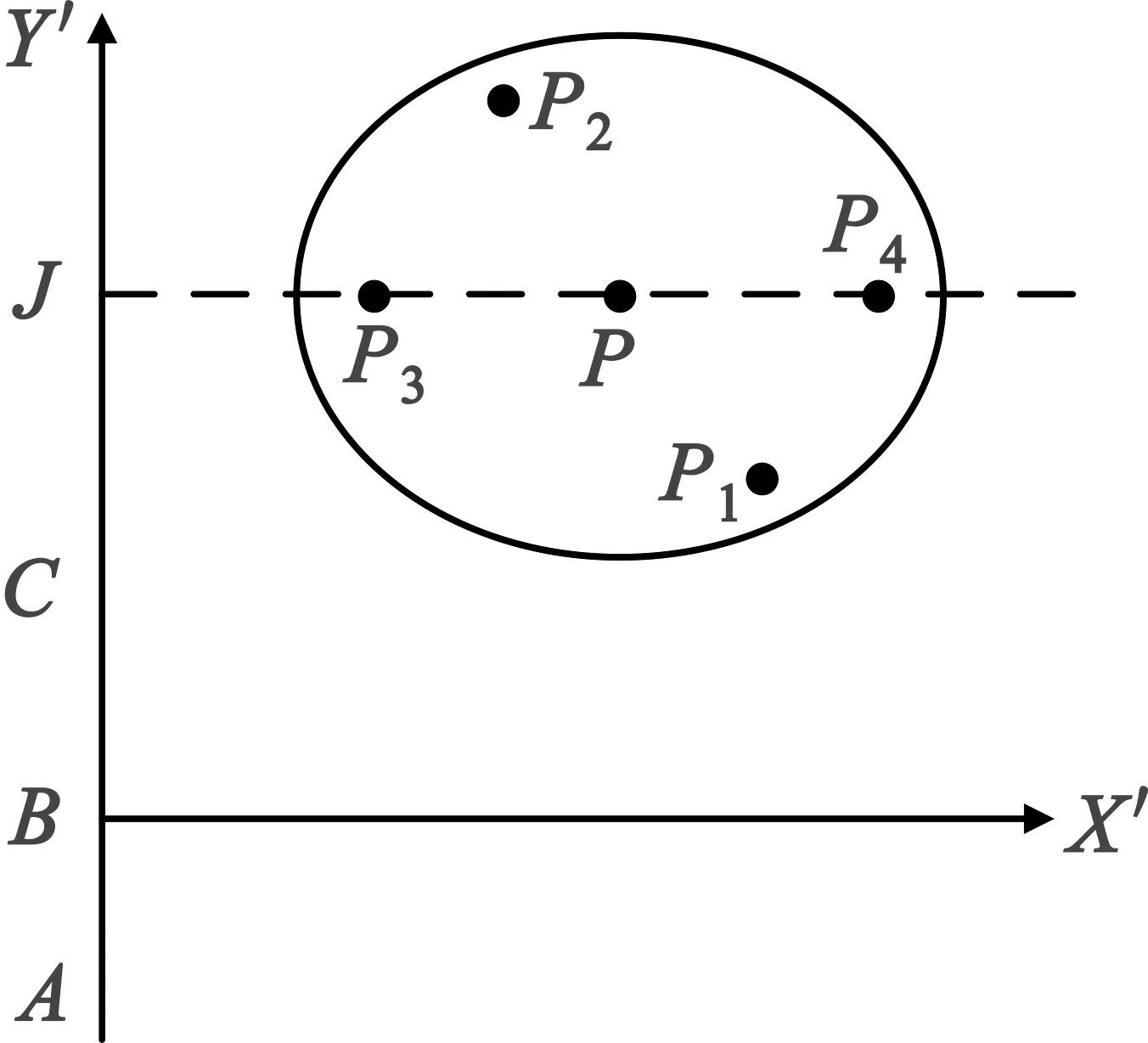
图2 多点目标在等效成像平面中的示意图

从上面的分析可以看出，由于实际成像的斜平面存在几何畸变，因此不能真实反映各目标点的物理空间关系，不能应用于后续的景象匹配或目标特征识别，因此需要从成像的斜平面向地平面进行投影，修正畸变的图像。

1.2 大前斜SAR成像几何校正原理分析

由于SPECAN成像算法具备大前斜成像场景适应性，且运算量相对较低，适用于弹载实时成像，在此开展基于该成像算法的几何校正原理分析[7,12]。

从SAR成像的斜距图到地面场景图像，其对应关系可以通过两次转换得到，首先需找到地面目标投影到等效成像平面的坐标关系，其次要得到等效平面坐标与最后SAR图像的坐标关系。

(1)地面到等效成像平面的坐标关系

在波束照射区内任选一点目标，在地面坐标系(详见图1)的坐标为(x,0,z)，其在等效成像平面(详见图2)的坐标为(x′,y′)。根据图2的几何关系，可得到以下的坐标变换关系。

(1)

式中：h为子孔径时间中心时刻平台的高度，α为下倾角。

(2)等效成像平面到SAR图像的关系

在等效成像平面等的点目标，经高阶相位补偿和二维聚焦成像处理后，其在SAR图像上的坐标为(R,fa)，则有如下坐标变换关系。

(2)

式中：V为孔径中心平台速度模值。

(3)SAR斜距图转地距图变换

由以上坐标变换关系，可得出SAR斜距图与地面点目标对应的变换关系为

(3)

由以上公式可得

(4)

式中：z的符号取决定于波束视线方向，在飞行方向右侧为正，左侧为负。

令子孔径中心速度矢量为V(vx,vy,vz)，式(4)可简化为

(5)

采用方向余弦定理，fa可表示为

(6)

式中：θg为前斜角(速度向量与视线夹角)地面投影，即地面方位角。

从式(5)可知，图像的畸变与导航参数中高度和速度精度相关。此外，参见式(6)，由于弹载成像条件下弹道下倾角α和下视角β一般在20°以上，希望方位角θg越小越好，然而当θg减小到20°以下时，多普勒将对速度误差十分敏感。接下来将详细分析参数误差对于图像畸变的影响。

2 弹道参数误差对图像畸变的影响

由式(5)可知，斜距图转地距图的几何校正过程中使用了子孔径中心时刻平台的高度和速度矢量信息，由安装在平台上的惯导提供，其速度和高度误差将导致投影坐标产生误差。

对于地面两个目标点(x1,0,z1)和(x2,0,z2)，它们之间的距离

(7)

两点间的绝对畸变量dL和相对畸变量ε定义为

(8)

由于微分方法应用于多变量非线性关系时，如果误差量并非小量，采用一阶微分会存在较大截断误差，不能直接用于分析图像畸变。如果要保证可用性，可考虑高阶Taylor展开，但理论形式和计算上都会变得非常复杂，故本文采取基于函数原型的差分计算方法。

记差分符号

ΔfΔx=Δf(x,Δx)=f(x+Δx)-f(x)，

(9)

其含义表示函数f(x)在x处因产生变化Δx而产生的变化量。

下面先分析x、z的差分，再通过x、z的差分计算L的差分ΔL和相对畸变量ε。

位置解算的差分表达式如下：

(10)

(11)

(12)

对于z的解算，考虑

(13)

有

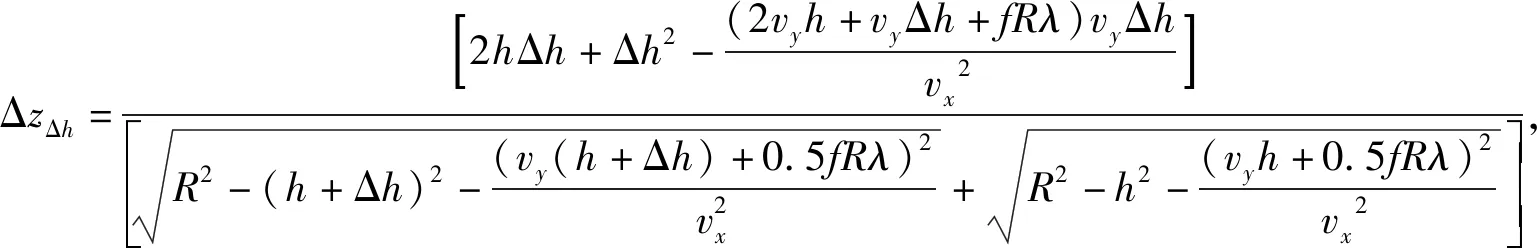
(14)

(15)

(16)

畸变量为

(17)

根据式(17)在计算ΔL分别对Δh、Δvx、Δvy的差分时，将Δx1、Δx2、Δz1、Δz2对Δh、Δvx、Δvy差分计算出来后代入最终得到图像相对畸变量。

3 仿真和实测数据结果

3.1 面目标几何校正仿真

作为对上述理论的验证，在此结合实际的应用指标进行仿真分析。仿真参数如表1所示。

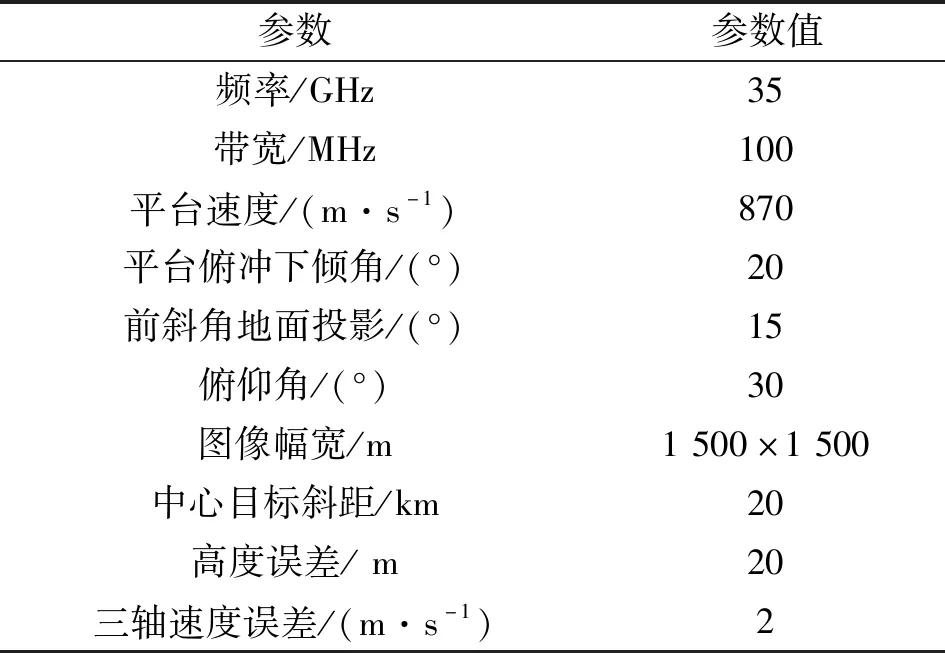
表1 仿真参数表

图3为大前斜SAR成像的斜距和地距图，该图为机场跑道及牵引道图像。从图3(a)可以看出，主跑道和牵引道本来是相互垂直的，但斜距图发生了严重的畸变，主跑道和牵引道成较大的钝角。图3(b)是几何校正结果，主跑道和牵引道成正常的垂直状态。从仿真结果可以看出，通过几何校正，实现了俯冲大前斜SAR图像从斜距到地距的准确转换。

图3 大前斜SAR成像仿真结果

该几何校正方法原理为距离多普勒域与实际空间地理坐系间通过斜距和多普勒关系的投影，其精度高。此外，本方案实现时采用地距图网格点反向查找距离多普勒斜距图点，并采用多倍上采样方式插值可大幅降低截断误差，提高图像质量。

该几何校正方法基于SPECAN成像算法，其校正的原理与文献[12]类似，但本文方法在实现层面的采用了多倍上采样插值后取临近点，虽然运算量相对较大，但截断误差小，精度更高，在参数无误情况下理论校正精度在1 pixel以内。

3.2 畸变误差分析

本文重点分析在各项参数存在误差情况下的图像畸变量，分析评估方法为在X轴和Z轴两个正交方向上，各自评估其几何校正后的相对畸变误差量在两轴方向的投影。以原点(0，0)为基准，分别在X轴和Z轴上以3 m的间隔设置评估点，成像距离范围为1.5 km，分别计算沿X轴方向和沿Z轴方向的评估点与基准点间实测值相对于理论值的误差。

根据高度和三维速度误差参数，采用蒙特卡洛方法每项参数按照1 000次进行仿真分析，并完成统计和计算相对畸变量。图4～6分别为仅单独考虑高度、X轴速度和Y轴速度误差对地距图相对畸变量的影响情况，图7是高度和三维速度误差为表1中仿真参数时其随方位角变化的联合影响情况。

图4 高度误差的影响

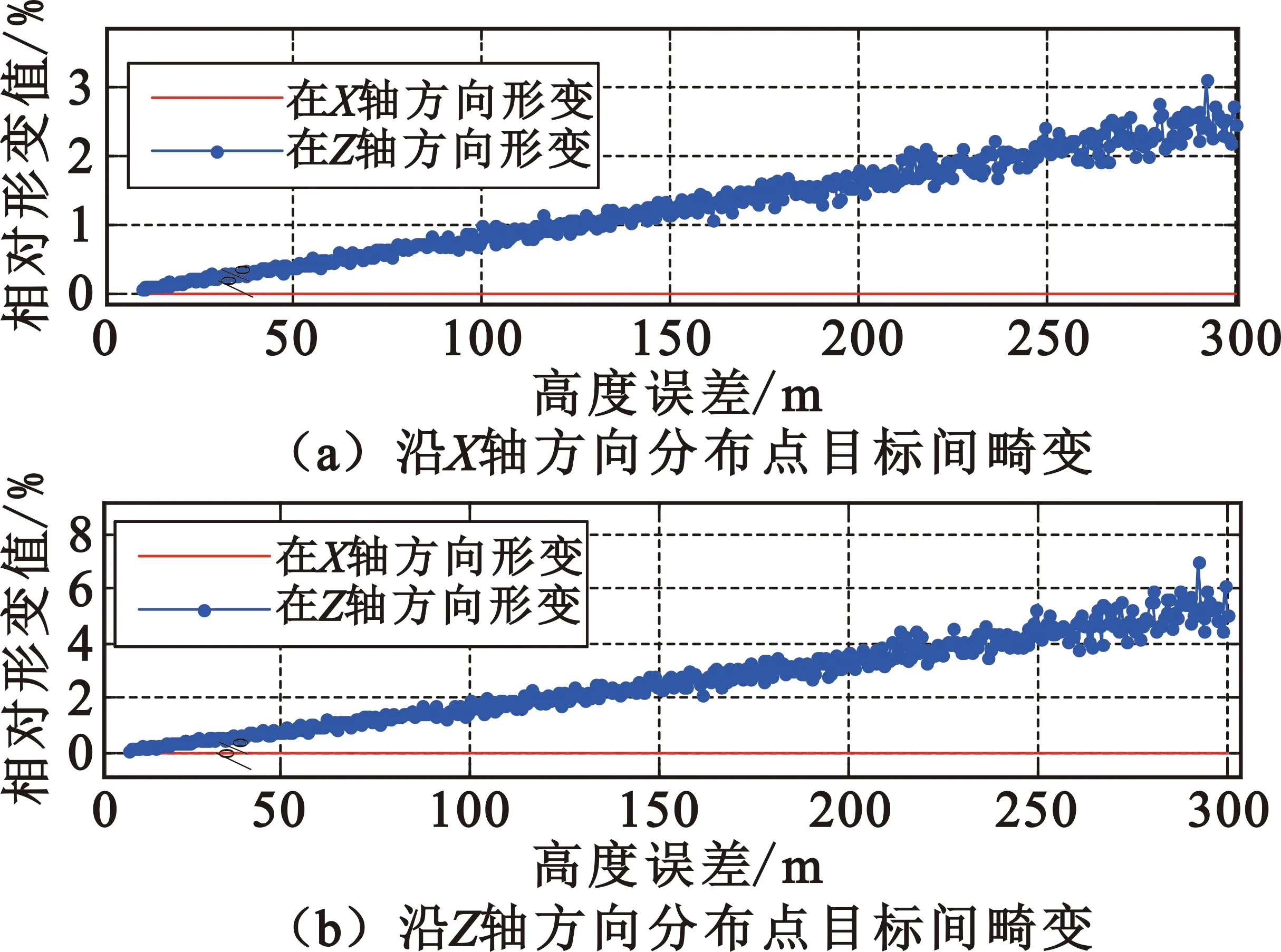
图5 X轴速度误差影响

图6 Y轴速度误差影响

图7 高度和三维速度误差一定时随方位角变化的影响

从图4～7可知，高度和速度误差导致的地距图畸变主要分布于垂直速度方向(Z轴)，而在速度方向(X轴)上较小；畸变量随高度和速度误差的增大而增加，随方位角的减小而迅速增加。

此外，由于不同方位角(前斜角在地面的投影角)情况参数误差对畸变量的影响不同，且在实际使用中地距图像地面坐标往往设置为距离像(波束视线方向)和方位向(垂直波束视线方向)，因此需在以上分析基础上绕Y轴进行旋转得到距离和方位向的畸变量。不同方位角和平台误差下地距图相对畸变误差如表2所示。

表2 不同方位角和平台误差下地距图相对畸变情况

从表2中可知，当方位角从20°减小到10°时，地距图畸变量将迅速增加，因此，在末端图像匹配或目标识别中需考虑该畸变量的影响。

4 结 论

本文针对弹载大前斜俯冲SAR成像几何校正算法进行了分析，重点推导并通过仿真和统计讨论了相关参数误差对地距图畸变的影响，其中，在方位角很小情况下，高度及速度误差对几何畸变量影响很大，在工程应用中需要将这两个参数量的误差或边界限定在一定范围内。仿真结果验证了理论分析的正确性。该研究为雷达导引头在成像模式下系统参数的设计提供了理论依据，并为后续的图像匹配或目标识别提出了相应需求，具有重要的工程应用价值。