基于EVM约束的预留子载波峰均比抑制*
杨 奎,刘志祥,刘 旺,王天乐
(1.中国西南电子技术研究所,成都 610036;2.上海交通大学 电子信息与电气工程学院,上海 200240)
0 引 言
正交频分复用(Orthogonal Frequency Division Multiplexing,OFDM)作为一种广泛使用的多载波调制系统,频域上各子载波相互正交,频谱利用率高,但其主要的一个缺点仍然是较高的峰值平均功率比(Peak-to-Average Power Ratio,PAPR)。高PAPR的信号会使高功率放大器(High Power Amplifier,HPA)工作在非线性区域,此时的HPA会使放大的信号产生不可逆的非线性失真,将会严重降低接收端的误码率性能(Bit Error Rate,BER)[1]。
预留子载波(Tone Reservation,TR)作为一种无失真峰均比降低技术,其复杂度较低,在实际通信系统中得到了广泛应用。传统TR技术严格要求预留子载波与数据子载波相互正交,占据的带宽受限因而其降低PAPR能力有限。在实际系统中,发送端一般容许数据信号中引入少量干扰。误差矢量幅度(Error Vector Magnitude,EVM)是许多无线通信标准(如WiMAX和LTE)中作为衡量发送端信号质量使用的指标。文献[2]中以PAPR和预留子载波功率为约束建立最小化信号EVM的非凸问题,通过运用半定规划(Semi-definite Programming,SDP) 将其转化为凸问题并求解。文献[3]中面对同样的问题,采用交替方向乘子法(Alternate Direction Method of Multiplier,ADMM)将原问题分解为多个简单的小问题。上述文献关注的都是信号的平均EVM,但其实数据子载波上存在的最大EVM更加直接影响着系统的误码率。
为了在发送端有更好的PAPR降低效果,本文提出改进TR技术,将传统的预留子载波扩展至数据子载波生成PCS,并对数据子载波上引入的干扰加上最大EVM约束。基于此思想,提出了基于EVM约束的TR优化问题,并采用凹凸过程(Concave-Convex Procedure,CCCP)[4]优化算法进行求解。仿真结果表明,所提出的基于EVM约束的TR算法在接收端的误码率略有下降,但是其在发送端有更加优秀的PAPR抑制效果。
1 系统模型
1.1 OFDM模型
考虑一个OFDM系统,其中每个符号由N个子载波组成,每个子载波上承载着M-QAM调制符号。原始频域信号可表示为X=[X0,X1,…,XN-1]T,其中Xk是频域第k个子载波的已调制信号。通常对离散信号进行4倍过采样以逼近连续信号的PAPR计算[5]。对频域信号进行L倍过采样后,得到离散的基带OFDM时域x=[x0,x1,…,xLN-1]T信号为
(1)
式中:L为过采样因子。
对频域信号进行快速傅里叶逆变换(Inverse Fast Fourier Transform,IFFT)可以得到时域信号x,该过程可表述为
x=IFFT(X)=QX。
(2)
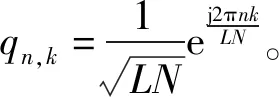
1.2 峰均比降低技术
1.2.1 峰均比定义
信号x=[x0,x1,…,xLN-1]T的PAPR可用公式表示为[6]
(3)
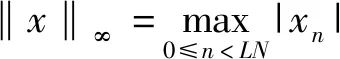
CCDF=P(PAPR>z)=1-(1-e-z2)N。
(4)
式中:z表示设定的PAPR门限。
1.2.2 预留子载波技术
预留子载波的基本思想是在N个子载波中预留Nr个子载波用于传输峰值消除信号,剩余N-Nr个数据子载波用于传输数据[7]。TR基本原理图如图1所示。

图1 预留子载波技术基本原理图

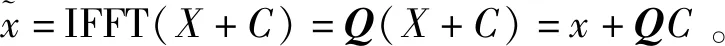
(5)
那么,在给定时域信号x的情况下,经过TR后OFDM信号的PAPR即可定义成一个关于变量C的函数,即
(6)
本文定义近似PAPR为
(7)

2 EVM-TR算法
2.1 问题建模
误差矢量幅度是一种测量信号带内失真的度量,是星座点Z相对于原始频域信号X的偏差量。其定义为误差矢量信号平均功率的平方根值和参考信号平均功率的平方根值之间的比值,即
(8)
传统的TR算法由于严格遵守预留子载波和数据子载波之间相互正交的约束,所以即使能在预留子载波集合上取得最优的峰值消除信号,其降低PAPR的能力也是有限的。因此,本文考虑牺牲一小部分的误码率以换取更好的PAPR降低效果,即将C原来只在预留子载波上存在有效值扩展至数据子载波上也存在有效值。但是,C在数据子载波上的扩展也是有约束的,相比于考虑平均的带内失真偏差,本文更关心数据子载波上出现的最大EVM偏差。当最大EVM偏差能够控制在有效的范围内时,接收端的误码率也能够有好的表现。
因此,结合考虑数据子载波上的最大带内失真约束,定义OFDM信号新的PAPR问题(EVM-TR)如下:
问题1:原始问题
(9a)
(9b)
(9c)
式中:α为预留子载波的功率阈值;β为数据子载波最大EVM阈值;矩阵MD和MR是二进制对角阵,维度均为N×N,分别对应着数据子载波位置和预留子载波位置,即
(10)
根据矩阵MD和MR的定义,则有
(11)
2.2 算法求解
问题1中,需要最小化的目标函数是优化变量C的凸函数。问题1中约束A1是优化变量C的非凸约束,约束A2是优化变量C的凸约束。因此,问题1是一个难于求解的非凸问题。通常,求解非凸问题的目标是求得其稳定点(Stationary Point)或其等价问题的的稳定点。问题1的稳定点不易求得,接下来求其等价问题的稳定点。首先,对问题1中不等式约束A1作等价变形,将问题1等价转化为以下优化问题:
问题2:问题1的等价问题
(12a)

(12c)
然后求解问题2,而非问题1。问题2仍然是一个不易求解的非凸问题。通过观察发现,问题2中约束A1具有凸函数减凸函数的结构,因此约束A1为DC(Difference of Convex Function) 函数,而问题2的目标函数和约束A2为凸函数,所以问题2是一个DC规划(DC Programming)问题。下面提出基于CCCP的迭代算法求得问题2的一个稳定点。

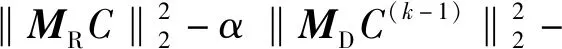
(13)

问题3:第k次迭代时问题2的近似问题
(14a)
s.t. A1:h(C(k-1),C)≤0;
(14b)

(14c)
问题3中,需要最小化的目标函数是凸函数,约束A1和约束A2都为凸约束,因此问题3是凸问题,可以利用内点法求得该问题的全局最优解。问题3包含N个优化变量和两个凸约束,利用内点法求解该问题的复杂度为O(N3)[8]。
基于CCCP求解EVM-TR算法(算法1)的具体算法伪代码如下:
输入:x,Q,MD,MR以及收敛精度
输出:C
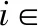
重复
k=k+1;
求解问题3,得到C(k);
直到‖C(k)-C(k-1)‖2≤
基于文献[9]中的结论,可以得到算法1的收敛定理如下:
定理1 算法1的收敛性。算法1的任何一个收敛点都是问题2的一个KKT点。
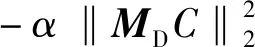
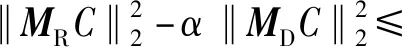

h(C(k-1),C)。
(15)
然后,根据文献[9]的定理1,可以证得结论。
证毕。
3 仿真结果与分析
为了验证所提出的基于EVM约束的TR算法降低PAPR的性能,基于Matlab环境做了OFDM系统下的仿真实验。设置预留子载波个数与总子载波个数的比例为1∶16。虽然文献[7]表明预留子载波位置随机时的PAPR效果优于固定位置,但是从工程实现的角度考虑,为了便于工程实际应用,选择预留子载波的位置为连续,其与数据子载波的位置关系如图2所示。

图2 预留子载波位置示意图
选择4-QAM调制方式,设置预留子载波位置为连续,信道为加性高斯白噪声(Additive White Gatssian Noise,AWGN)信道,其余相关仿真参数如表1所示。

表1 仿真参数设置
为了更好地展现所提算法的PAPR减少效果,本文将其与两种现有的改进TR算法(TKM-TR[10]、MS-SCR[11])进行比较。
3.1 PAPR性能
图3给出了上述三种TR算法的PAPR减少性能的对比。它们与EVM-TR算法具有相同的预留子载波集合设置,其中TKM-TR和MS-SCR的削峰比(Clipping Ration,CR)设置为5 dB。当CCDF=10-3时,原始OFDM信号的PAPR为11.2 dB。分别使用TKM-TR和MS-SCR算法经过三次迭代后,PAPR可以近似被减少到8.1 dB和7.1 dB。所提出的基于最大EVM约束的TR算法随着EVM数值变大,其PAPR相应减少得更多,从EVM为5%,PAPR削减到6.9 dB,增加到EVM为8%,PAPR削减到5.6 dB。从图中可以看出,所提算法的CCDF曲线衰减得更快,由此可知EVM-TR算法具有更优的PAPR抑制性能。

图3 不同算法PAPR降低效果比较
3.2 误码率性能
图4比较了上述各种算法在AWGN信道下的误码率性能。其中,TKM-TR与MS-SCR的迭代次数为3次,削峰比为5 dB。在BER为10-4时,当发送端的EVM值分别为5%、6%时,EVM-TR算法在接收端的误码率与原始OFDM信号近似相等;而当发送端EVM增大到8%时,接收端的误码率损失约1 dB,而考虑到此时发送端的PAPR减少了约5.6 dB,因此误码率性能的下降是可以接受的。

图4 不同算法在AWGN信道下的BER性能比较
4 结 论
本文提出了一种基于EVM约束的TR算法,将传统TR算法中只由预留子载波生成峰值消除信号扩展至数据子载波生成峰值消除信号,并在此基础上加入数据子载波上会因此出现的最大EVM偏差约束,以保证系统的误码率处于有效范围内。由于有效使用了数据子载波,其PAPR性能相比于传统TR算法有明显提升。仿真结果表明,与传统的TR算法相比较,所提出的基于EVM约束的TR算法能以1 dB的接收端解调性能损失换取发送端5.6 dB的PAPR抑制效果。

