A new accelerating technique for low speed flow:Pseudo high speed method

Hito DONG , Fujun LIU

a NLCFD, School of Aeronautic Science and Engineering, Beihang University, Beijing 100083, China

b China Aerodynamic Research and Development Center, Mianyang 621000, China

KEYWORDS Artificial speed of sound;Euler equations;Low speed flow;Navier-Stokes equations;Precondition method;Pseudo High Speed (SHS)

Abstract This paper proposes a new accelerating technique for simulating low speed flows,termed as pSeudo High Speed method (SHS), which uses governing equations and numerical methods of compressible flows. SHS method has advantages of simple formula, easy manipulation, and only need to modify flux of Euler equations. It can directly employ the existing well-developed schemes of hyperbolic conservation laws. To verify the technique, several numerical experiments are performed, such as: flow past airfoils and flow past a cylinder. Analysis of SHS method and comparisons with some precondition methods are made numerically. All tests show that SHS method can greatly improve the efficiency of compressible method simulating low speed flow fields,which exhibits in accelerating the convergence rate and increasing the accuracy of the numerical results.

1. Introduction

In the development of Computational Fluid Dynamics(CFD),the numerical methods of compressible flow are welldeveloped, and many noted high resolution and high order schemes have been constructed.These methods are successful and have been widely used in the computations of subsonic,transonic, supersonic and hypersonic flows. However, these methods suffer degradation in performance when low speed flow fields(Ma ＜0.1)are simulated,namely,slow convergence and wrong-convergence(poor accuracy)problems:the computation becomes very slow and often can not obtain correct results. In theory, equations of compressible flow are true for flows at any speeds, including the case of zero velocity, so the problem of low speed computations appears rather bewildering. Originally the explanation about this phenomenon is: the large disparity between eigenvalues of the flow field produces stiffness when it tends to incompressible flows. Two types of approaches have been developed: (A) incompressible method and artificial compression method;(B) precondition method.Then researchers found convergence and accuracy are two separate difficulties,and some researchers pointed out that the latter is because of the loss or excess of dissipation.3The cures for these problems are different.For convergence the time derivative is preconditioned.For accuracy the artificial dissipation is modified.It should be noted that the reasons of accuracy problem are many and varied,and numerical dissipation is just one of the explanations.

There are many forms of precondition methods, the precondition matrix is not unique, and the variables used may be primitive or conservative.Four kinds of precondition methods are used more often: Turkeloriginating from artificial compression method,proposed a precondition matrix containing two parameters, using primitive variables of (ρ,u,v,w,S);van Leer et al.proposed a so called optimal preconditioner which may obtain the lowest condition number; Choi and Merkleproposed a simple diagonal precondition matrix,using primitive variables of (ρ,u,v,w,p); Weiss and Smithobtained a precondition matrix by making using of the transformation from conserved variables to primitive variables(ρ,u,v,w,T). Other developments and applications in precondition method:Leestudied the convergence characteristic of precondition method and the effect of condition number;Zaccanti and Cinnellatmade a comprehensive analysis on precondition methods of van Leer et al. and Turkel, and listed a series of design criteria for the preconditioner; Turkel and Vatsadiscussed the choice of variables of precondition method;Venkateswaran et al.studied the sensitivity of preconditioning algorithms to pressure disturbances and proposed a linearized preconditioning methods for enhancing the robustness and efficiency; van Leer et al. and Turkeland Venkateswaran et al.investigated the robustness of precondition method in stagnation regions; Li and Gudesigned an all-speed Roe scheme based on precondition method; de Medeiros and de B Alvesstudied the stiffness, sensitiveness and robustness in preconditioned density-based methods at low Mach number;Requier and Duquesneinvestigated the use of precondition method in flows containing both incompressible and compressible zones, such as boundary layer problems; Gupta et al.and Huangdeveloped a preconditioning method for a multiphase compressible flow with cavitations; Potsdam et al.simulated the unsteady flow of a whole rotorcraft utilizing precondition method; Tweedt et al.simulated the flow of turbomachine blade rows with a preconditioning scheme;Darmofal and Schmidstudied the eigenvectors of local preconditioner; Vatsa and Turkelstudied local preconditioners for steady and unsteady flows, and they pointed that the preconditioner should be included in artificial viscosity or upwinding terms, and expressed the algorithm in several sets of variables while using only the conservative variables for the flux terms; Rossowproposed a Runge-Kutta/Implicit method for increasing the computing efficiency, and for low speed flow he expressed the inviscid flux Jacobians in terms of Mach number and introduced an artificial speed of sound,and he also studied the stiffness in the discrete equations associated with highly stretched meshes (It should be noted that,there is no such stiffness for the methods using dimensional splitting technique); Swanson et al.developed Runge-Kutta/implicit further and extended to 3D RANS equations;Peles and Turkelinvestigated the Rossow-Swanson-Turkel Runge-Kutta/implicit scheme as a convergence accelerator for complex multi-physics flow problems including turbulent,reactive and also two-phase flows. Langerpointed that convergence and accuracy are two separate problems, and the word ’precondition’ is misleading in some context, but is used until now in consideration of originality. He also pointed that the word ’modification’ seems to be more appropriate. Chen et al.developed a low-diffusion flux splitting scheme termed TVAP, which can achieve the simulation of wide-ranging Mach number flows. They pointed out that typical upwind schemes(e.g.Roe and TV)have loss of accuracy at low speeds as a consequence of the excessive numerical viscosity,while the low Mach behavior of TVAP scheme fits well with the properties of the idea Euler equation. Han et al.presented and investigated a combination of matrix precondition and multigrid method, and the results shown that it is efficient and robust for both compressible and incompressible flows and is attractive for aerodynamic optimization.With a preconditioning finite volume method, Fan and Xiasimulated the parachute transient dynamics, and they also extended Roe and HLLC scheme to compute flow problems at all speeds. Chen et al.devised an improved farfield boundary condition to the preconditioning equations based on characteristic relations, which improved convergence rate and accuracy of low speed incompressible flow computations.

At present, precondition method has been widely used in simulations of low speed compressible flow fields, and it enhances computational efficiency obviously. Though the preconditioning matrix is a little complex in construction and brings some extra manipulations, the point is mainly at explanations of convergence problems. We are more interested in two contradictions: (A) if the reason of slow convergence and poor accuracy is the large disparity of eigenvalues, then why there is no such problem for transonic cases with the same large disparity of eigenvalues? (B) in some cases, the convergence is not very slow,but the solution is bad even with double precision data in computing. Since the low convergence and poor accuracy mainly occurs in low speed flow fields, we consider Mach number to be a key factor of this trouble.Inspired by this observation, we propose a new method, pSeudo High Speed (SHS) method, which increases pseudo Mach number in pseudo time steps and keeps physical Mach number unchanged, then the convergence rate of computation can be accelerated,and the correctness of computation is guaranteed.

The outline of the following sections is as follows:Section 2 presents brief philosophy of the new method, as well as the detailed deduction of formulas; Section 3 presents the characteristic systems; Section 4 gives numerical schemes; Section 5 presents the numerical experiments performed on typical low speed flows, such as flow past NACA0012 airfoil, flow past S809 airfoil and flow past a cylinder;Section 6 makes analysis of SHS method and comparisons with precondition method and method of artificial sound speed, and the mechanism of why SHS works for low speed problems.

2. Ideas of pseudo high speed method and its deduction

The problem of low speed flow was considered to be the stiffness problem, and employed precondition matrix to lower the condition number.Then researchers realized that the slow convergence and poor accuracy are two separate problems, and the accuracy problem can be improved by modifying numerical dissipation. Because the choice of preconditioning matrix is not unique,we have tried to design different preconditioning matrix based on the idea of narrowing the discrepancy among eigenvalues (some way like things done by van Leer et al.),but the results are not satisfactory(in most cases,the deduced eigenvalue formulas are too complex to be used).

From a new point of view, we give another explanation of convergence, namely, the mechanism lies in Mach number,since computations of flow fields with high Mach number converge fast and correct. According to this idea, we modify pseudo-time term, making Mach number increases in pseudo procedure, while keeping it unchanged in physical procedure.Then the trouble of slow convergence and mis-convergence can be overcome by computing the low speed flow fields using a pseudo procedure of high Mach number.This is why the new method is named as SHS method,which mainly modifies Euler equation, and can be applied on Navier-Stokes equations almost without any change (see Appendix A). Therefore, we take Euler equations as an example to demonstrate the deduction of SHS method.

The SHS method is constructed as follows:(A)add pseudo time derivative term, and use dimensional split in pseudo time step; (B) increase the Mach number of free stream in pseudo time step and keep it unchanged in physical time step,and this can be realized through multiplying a small parameter to density in pseudo time step while keeping velocity, pressure unchanged.Since the modifications are made on pseudo terms,the physical relations are not affected. Comparing the pseudo term with physical flux,the decrease in density is equivalent to the increase in velocity, and therefore the Mach number increases in pseudo time steps.

Consider the following three-dimensional Euler equations in curvilinear coordinates.where θ is pseudo time which is equivalent to iteration number of solution which converges to the physical solution when θ→∞. Note that, the first term is the pseudo time derivative,while the second and the third are physical terms. It can be seen that modifying the pseudo term dose not affect the physical relations after convergence.Eq.(1)and Eq.(5)are all original equations, the latter is suitable for methods from steady problems extending to time dependent problems.

Second, multiply a small positive parameter κ to density in pseudo term:

Comparing pseudo term with flux, it can be seen that convective velocity is increased (viewing 1/κ and eu+ev+ew together). However, comparing physical term with flux, the velocity is unchanged. Note: for steady problems, the physical time derivative term (·)is omitted in Eq.(7).

Third, restore the density to real one via dividing it by κ:

where ρmeans true density, and this is the final step.

The Navier-Stokes equations of SHS method is put in Appendix A.

Summary. Let us see how the pseudo Mach number varies in different steps: (A) decreasing the value of density by κ times, the Mach number is lowered by times according to sound-speed formula; (B) applying decreased density to pseudo time term, keeping the physical terms unchanged, in view of flux, the convective velocity is increased by 1/κ times,while the sound speed is unchanged, then the Mach number is increased by 1/κ times; (C) restoring the density, the overall effect is that the Mach number is increased by times. Of course, this is just a rough analysis. For details, we need to derive the characteristic system of SHS method.

3. Characteristic system of SHS method

We use dimensional splitting method computing a 3D problem by several 1D schemes. Split the Eq. (7) into three 1D equations via operator splitting techniquein pseudo time steps:

where n is dimension (n=1 for 1D, n=2 for 2D, n=3 for 3D).

To deduce eigenvalues and eigenvectors conveniently, we rewrite Eq. (9) as Eq.(10). Let u=eu+ev+ew,for perfect gas, the SHS method is

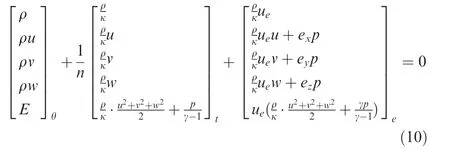
For steady problems,the physical time derivative term(·)is omitted in Eq.(10).First,review the eigenvalues and eigenvectors of original Euler equations.The Mach number is defined as Ma=u/ c, and the flow is subsonic if u＜c. The last two lines of eigenvector matrix in Eq. (11) are put in Appendix B.

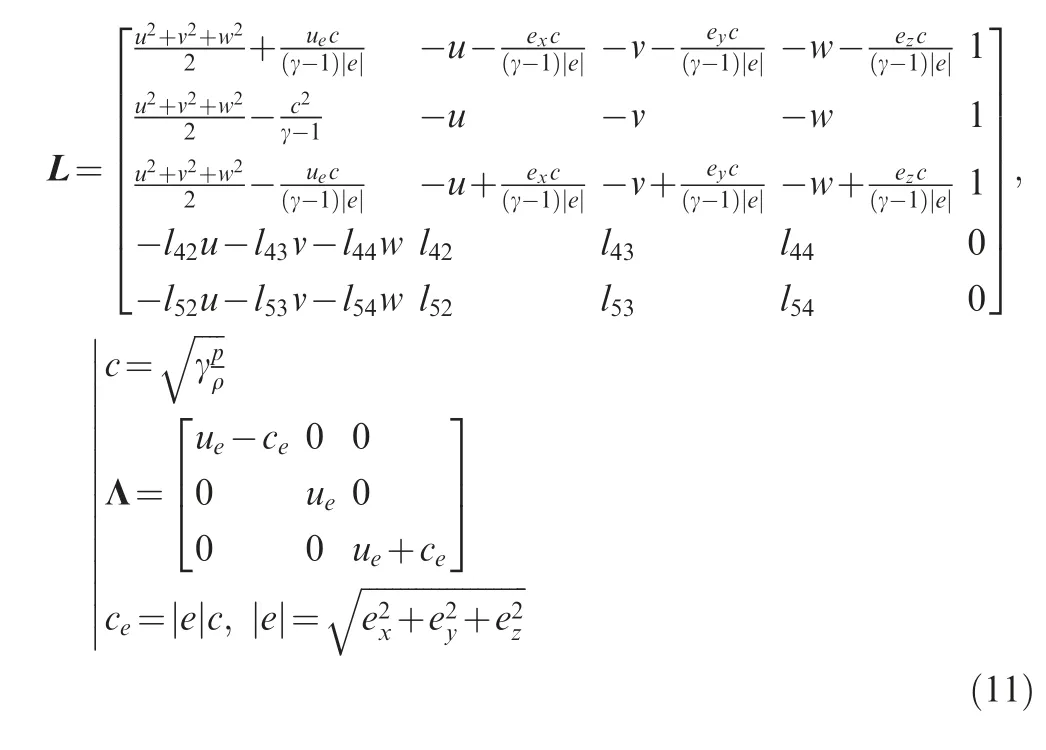
Finding Jacobian matrix of flux with respect to pseudo conservative variables for Euler equations in SHS method,the exact pseudo Mach number can be obtained by solving eigenvalues and eigenvectors of the matrix. The obtained eigenvalues and eigenvectors in pseudo procedure are given as follows:

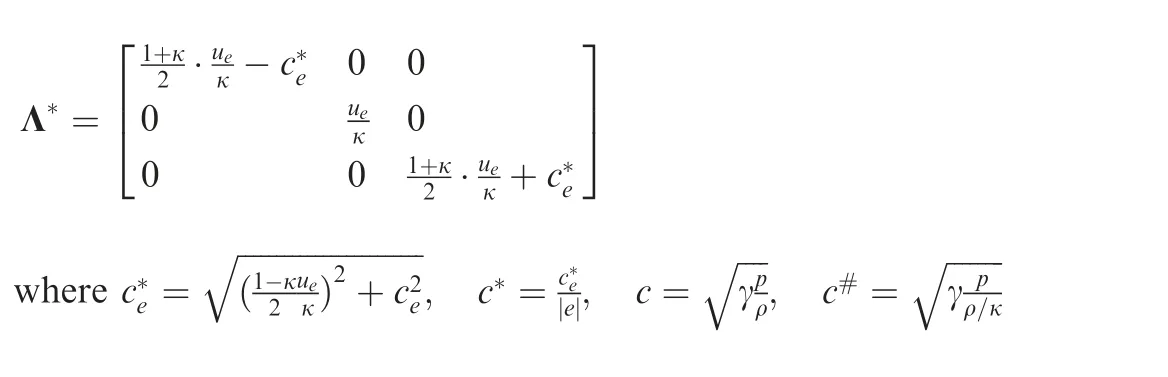
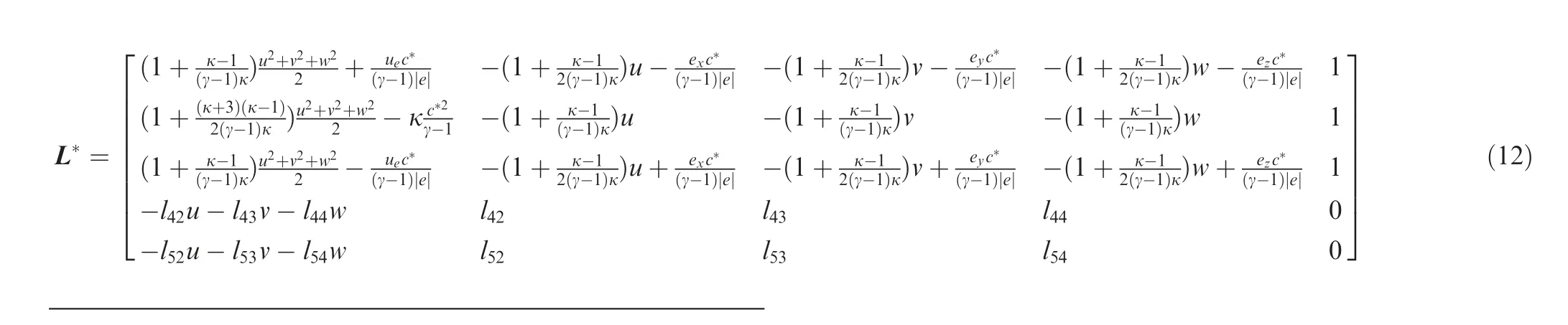
where the last two rows of pseudo left eigenvectors L* are the same as those of original L(see Appendix B).Changing density in pseudo term is equivalent to changing the sound speed of pseudo time step, but the physical relations are not changed.Although this modification enhances sound speed, it enhances convective velocity more, so the Mach number is enhanced.The definition and exact formula of pseudo Mach number is as follows:

Note: when κ=1, the equations return back to the original ones.

4. Numerical schemes

Numerical schemes of SHS method are same with those of original equations.We choose the second order entropy condition scheme,and use dimensional split technique in multidimensional cases. Since the numerical tests in this paper are all time independent, we give only the steady scheme of SHS.Omitting the physical time term (˙s), we rewrite Eq. (10) as follows

where f(u),L(u)are respectively the numerical flux,left eigenvectors that are modified by entropy conditions, Θ(·,·) is the function of limiter (minmod limiter is used in this paper), for details, refer to Refs.. The 2nd order entropy condition scheme is constructed via the 2nd order interpolation of the exact solution of the linearized equations with flux embedded with entropy condition.Comparing to Harten’s TVD scheme,this scheme has a smaller numerical viscosity and exactly satisfies entropy condition and keeps 2nd order accuracy.

5. Numerical experiments

In this section, we verify SHS method numerically, and compare it with original equations, with low speed flows. Three numerical experiments are made:flow around NACA0012 airfoil, flow around S809 airfoil, flow past a cylinder.

Test 1. Inviscid flow past NACA0012 airfoil

The flow past NACA0012 airfoil is a typical example in CFD, and the experimental data is abundant. To validate SHS method, we choose the free stream condition as Ma=0.01, α=0°. The computational grid is shown in Fig. 1, which is made up of 239×59 cells (flow direction×normal direction). The SHS method parameter κ=4×10, and the pseudo Mach number Ma*=0.485082. The experimental data is taken from Gregory and O’Reilly.

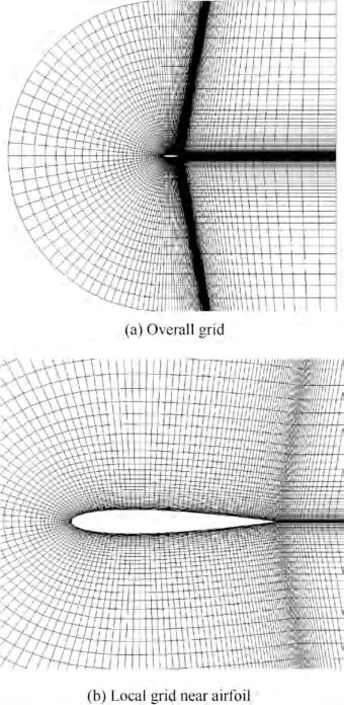
Fig. 1 Grid of NACA0012 airfoil.

In this test,the angle of attack is zero which causes symmetric pressure coefficient Cdistribution, as shown in Fig. 2 and Fig. 3. For original method, the pressure contours are not smooth and have many oscillations,and the pressure distribution dose not agree well with experimental data. The pressure contours and distribution are improved greatly via SHS method,and the convergence rate is also accelerated,as shown in Fig. 4

Test 2. Inviscid flow past S809 airfoil

S809 is a low speed airfoil designed for wind turbine blade,and the maximum relative thickness is 21%. The Mach number of free stream is taken as Ma=0.01, and the angle of attack is α=5.13°. The size of computational grid is 440×60 (flow direction×normal direction), as shown in Fig.5.The SHS method parameter κ=4×10,and pseudo Mach number Ma*=0.485082. The experimental data is taken from Wolfe and Ochs.

For original method, pressure contours have many oscillations, as well as the pressure distribution which is completely unacceptable, as shown in Fig.6(a) and Fig. 7. With SHS method,pressure contours become smooth and pressure distribution matches very well with experimental data, as shown in Fig.6(b) and Fig. 7. In Fig. 8, it can be seen clearly that, for original method, the convergence is dismal, while, for SHS method, the convergence is tremendously fast.

Fig. 2 Pressure contour around NACA0012 airfoil.

Fig. 3 Comparison of pressure distribution for Test 1.

Test 3. Viscous flow past a cylinder

Low Reynolds number viscous flow past a cylinder is also a typical example for Navier-Stokes equations.A pair of recirculation bubbles is formed behind the cylinder and its length increases with Reynolds number. The pressure distribution on the surface of cylinder and the length of recirculation bubble are important characteristic for verifying numerical methods. In this test, we take inflow Mach number as Ma=0.001, and Reynolds number as Re=20, which is defined by inflow speed and diameter of the cylinder. The Omesh is used, which consists of 301×201 grid points, and it is refined near the wall and recirculation bubbles, as shown in Fig. 9. The parameter of SHS method is κ=4×10,and pseudo Mach number is Ma*=0.157622.The experimental data is taken from Fornberg.

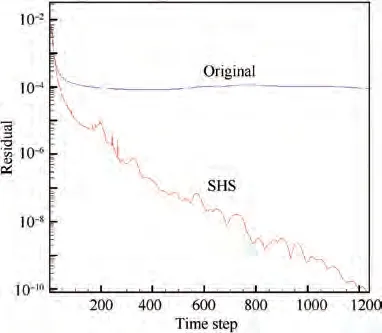
Fig. 4 Comparison of convergence history for Test 1.

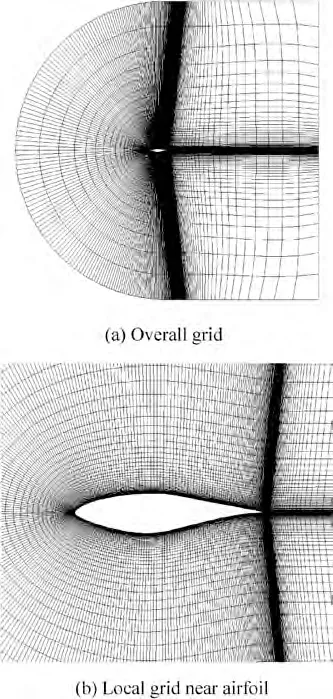
Fig. 5 Grid of S809 airfoil.

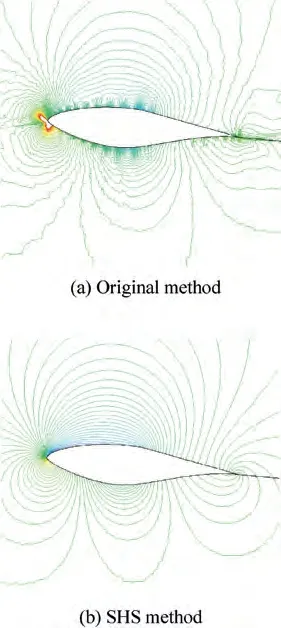
Fig. 6 Pressure contour around S809 airfoil.

Fig. 7 Comparison of pressure distribution for Test 2.

For original method, the pressure contours have many oscillations, and the length of recirculation bubbles is also incorrect,which makes false pressure distributions on cylinder surface. Using SHS method, the pressure contours become smooth and the pressure distributions are correct, as shown in Figs. 10-12. Table 1 lists the lengths of recirculation bubbles,which shows that SHS method has a good agreement with standard results.Fig.13 shows the comparison of convergence histories between original method and SHS method, from which it can be seen that the acceleration effect of SHS is prominent.

6. Analysis and comparisons

6.1. Perplexity of condition numbers

In this subsection, we investigate the effect of condition number and Mach number on convergence using original equations, and reveal a perplexity which has many explanations by other scholars.

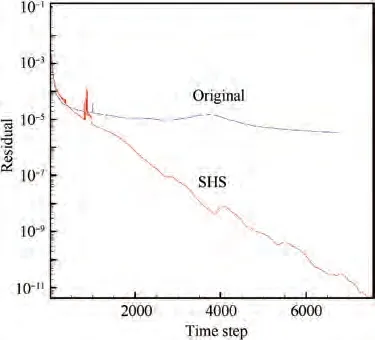
Fig. 8 Comparison of convergence history for Test 2.

The stiffness problem originally comes from Ordinary Differential Equations (ODE), which means large disparity of eigenvalues or large condition number for matrix of the ODE equations. In fluid dynamics, Mach number is usually used as an indicator to distinguish between compressible and incompressible flows, while, Navier-Stokes or Euler equations are not ODE equations and their condition numbers have different roles from that in ODE case. For Euler equations, the condition number is large both at low speed case and transonic case,but only low speed flows have trouble of slow convergence and poor accuracy.Stiffness problem in ODE case can be overcome by implicit method,while the problem in low speed flow can not be solved merely via implicit method.Turkelalready pointed out that the difficulties are caused by two different reasons and accuracy problem has nothing to do with the condition number.Now,we give a test to check the relations between convergence property and Mach number, condition number.

Mach number test. Convergence property of original equations

The computations are performed on flow past NACA0012 airfoil with mesh 239×59, and the residual is 10(the residual is computed every 100 pseudo time).For simplicity,we use the following definition for condition number

Note: the ratio of max and min modulus of eigenvalues plays the same role as the condition number defined by matrix norm if the eigenvalues of the matrix are all real numbers, so we simply call the ratio as condition number,Turkel also used this definition for condition number.

Analysis of Table 2:

(1) The computation is not converged correctly for Ma=0.01.

(2) The computation is converged with large error for Ma=0.1.

(3) The condition number is minimum for Ma=0.5, and the convergence rate is fast.

(4) The condition numbers are large for Ma=0.9, 0.99, 1(the disparity of condition numbers among them is also large), however, the computations converge correctly at the same convergence rate.

Fig. 9 Grid of cylinder.

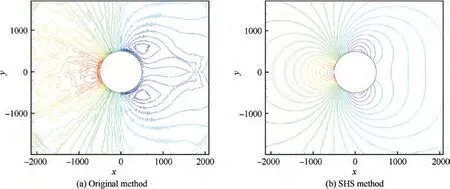
Fig. 10 Pressure contours around cylinder.

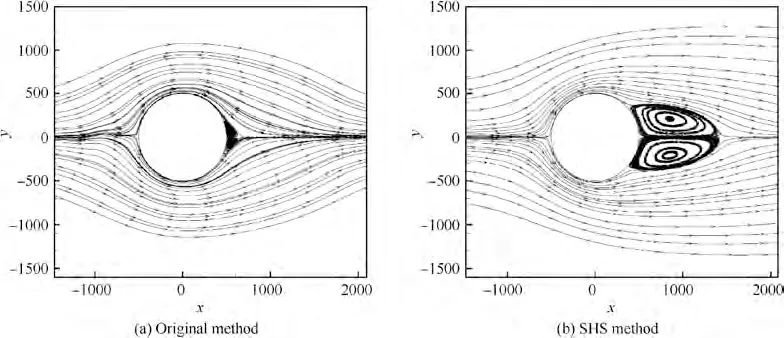
Fig. 11 Streamlines, Ma∞=0.001, Re=20.

Consequently, the convergence is mainly affected by Mach number.

6.2. Condition number vs pseudo Mach number

In this subsection, we investigate the effect of condition number and pseudo Mach number on convergence using SHS method.It has an advantage of using SHS method,that is,the comparisons can be made with the same free stream.First, we give the formulas of condition number and pseudo Mach number in SHS method.

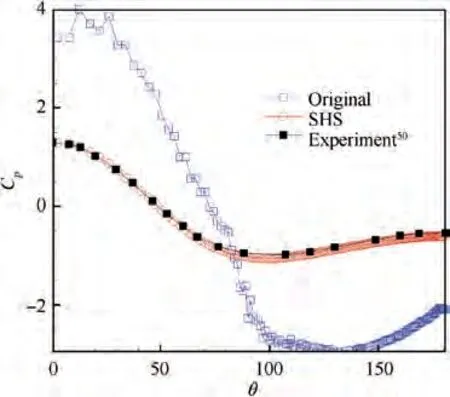
Fig. 12 Comparison of pressure distribution for Test 3.

Table 1 Length of recirculation bubbles (L/D).

Fig. 13 Comparison of convergence history for Test 3.

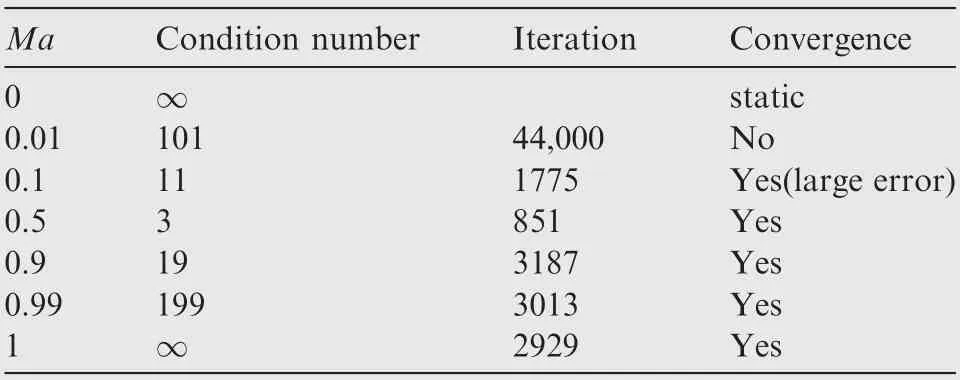
Table 2 Convergence of different Mach number of original method.

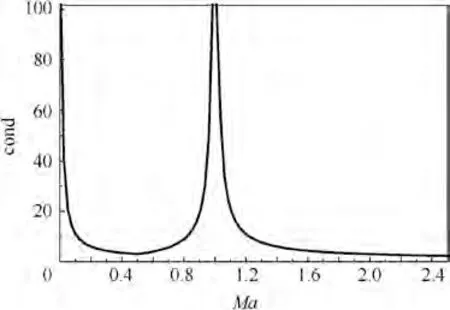
Fig. 14 Condition number of original equations.

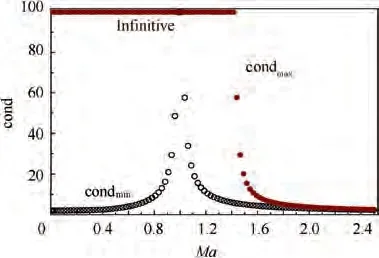
Fig. 15 Condition number at condmin and Ma*max.

Parameter Test 2. Transonic flow past NACA0012 airfoil.

The Mach number of free stream is Ma=0.818, the angle of attack is α=0.14°, and the parameter of SHS method is taken as κ=0.01, 0.2, 1, 0.0008, 4, 100, respectively. The residual history and pressure distributions for different κ are displayed in Figs. 20-21.

From Fig. 18, Fig. 20 and Table 3, it can be seen that the fastest convergence occurs around the smallest condition number, and the slowest convergence occurs around the largest condition number. Therefore, the convergence rate does have a good correlation with the condition number.While for accuracy,the best pressure distribution happens around the largest pseudo Mach number, and the worst pressure distribution

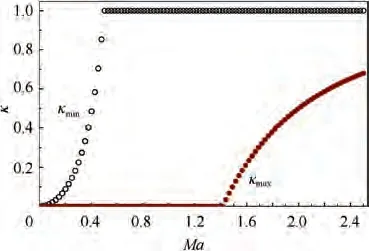
Fig. 16 κ at condmin and Ma*max.

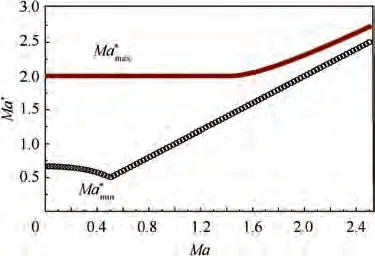
Fig. 17 Pseudo Mach number at cond_min and Ma*max.

Fig. 18 Residual history for parameter test1.

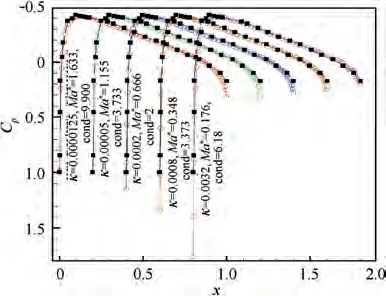
Fig. 19 Pressure distribution for parameter test1.

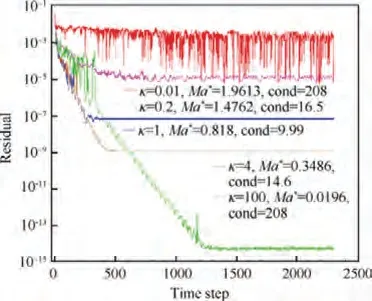
Fig. 20 Residual history for parameter Test 2.

happens around the smallest pseudo Mach number.Therefore,the accuracy of computations has a good correlation with the pseudo Mach number. Until now, SHS method has been verified completely,and we give following explanations about the acceleration mechanism. The problem of low speed flow is mainly wrong-convergence (accuracy problem), not slow convergence. Even if the computation converges, the error is also large. There is such a case, for which, the residual is already converged, but the result is not correct, such as the case of κ=0.0032 in Parameter Test 1, as shown in Fig. 18 and Fig.19,which corresponds to small pseudo Mach number and small condition number. There is also such a case, for which,the residual history is not good, but the result is correct, such as the case of κ=0.0000125 in Parameter Test 1,as shown in Fig. 18 and Fig. 19, which corresponds to large pseudo Mach number and large condition number. Both cases can not be explained by stiffness and condition numbers.We noticed that in former case the spatial variations of low speed flow are relatively small and sensitive to round-off error of difference discretization.

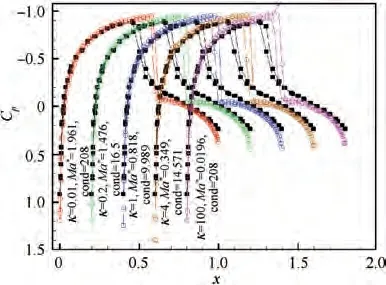
Fig. 21 Pressure distribution for parameter Test 2.

6.3. Comparisons between SHS and Weiss-Smith’s precondition method

SHS method can improve the computational results of low speed flows, and then people will naturally wonder how it differs from precondition method, and how are the comparisons of their efficiency. The main difference is that SHS method does not need a precondition matrix and its formulas are universal for both low and high speed flows.The common feature of the two methods is at the eigenvalues (almost same in shape), which make their convergence quite similar.

We use four forms of precondition method with Weiss-Smith’s preconditionerfor comparing: primitive variables and simplified precondition matrix, primitive variables and un-simplified precondition matrix, conservative variables and simplified precondition matrix, conservative variables and un-simplified precondition matrix. The advantage of using primitive variables is that the formula is relatively simple,but is not suitable for flows containing shocks. So, conservative variables should be used for high speed flows. According to Cao and Wu,for low speed flow,the method with simplified precondition matrix is more robust than that with unsimplified.However,for high speed flow,the type with conservative variables and un-simplified precondition matrix can return back to original equations. The four types of precondition method are denoted as ①, ②, ③, ④, and their formulas are given in Appendix C. Now we perform three comparison tests, the first two using precondition method with low speed flow, transonic flow respectively, the third using the method of artificial sound speed with low speed flow. For low speed flow,we use precondition method ①,and for high speed flow,the precondition method ④is used.

Comparison Test 2.Transonic flow past NACA0012 airfoil.

The Mach number of free stream is Ma=0.818, the angle of attack is α=0.14°. SHS method and precondition method④are used in this test,and the parameter of the two methods is taken as κ=0.2,1,40 respectively.The residual history and pressure distributions,given by the two methods with different parameter κ, are displayed in Figs. 24-25.

Comparison Test 3. Comparison with the method of artificial speed of sound (Art).The diagonal preconditioner of Choi and Merkleis used for simplicity and efficiency.The residual history and pressure distributions are displayed in Figs. 26-27.

Comparison tests analyzed in Table 4 show that: For precondition methods, in low speed flow, the type with unsimplified precondition matrix converges slower than the type with simplified precondition matrix; in flows containing shocks, conservative variables should be used, but the type with simplified precondition matrix does not work. Now For SHS method, it is applicable for all speed flow and has the same convergence rate with the optimum precondition method, and its parameter κ has less restriction, but sincethe control parameter range is not small for both methods,maybe this difference does not mean much; finally, it does not need a precondition matrix,and this saves some CPU time(about 10%) compared to precondition method.

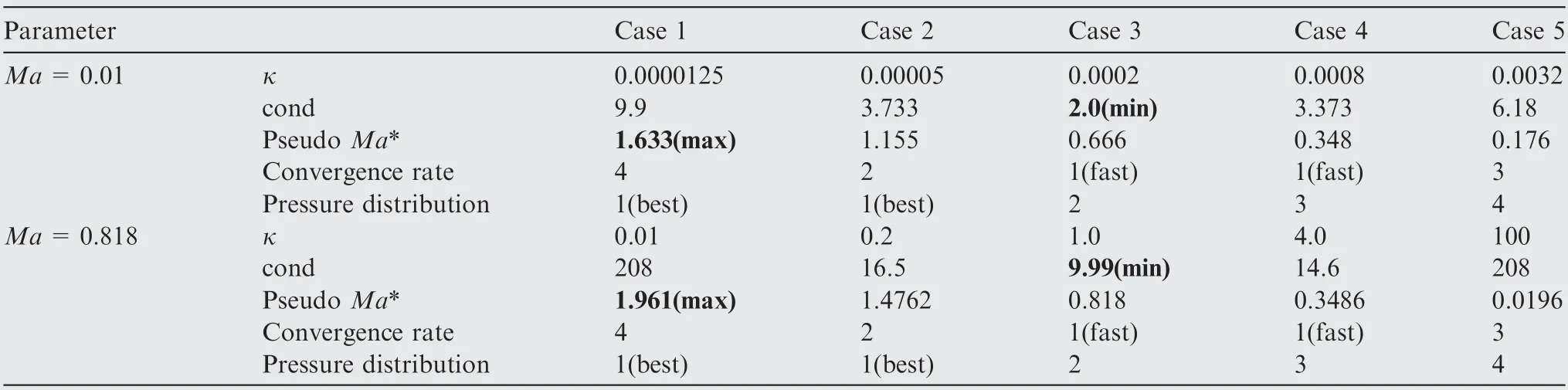
Table 3 Comparisons of different κ for parameter Test 1 and parameter Test 2.

Fig. 22 Residual history for comparison Test 1.

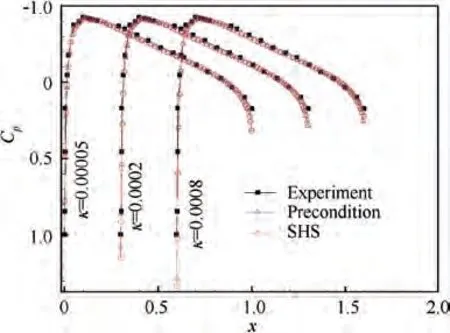
Fig. 23 Pressure distribution for comparison Test 1.

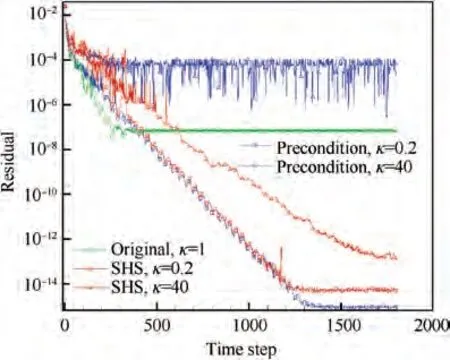
Fig. 24 Residual history for comparison Test 2.

6.4. Comparisons with density

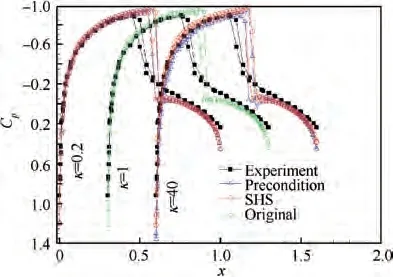
Fig. 25 Pressure distribution for comparison Test 2.

Fig. 26 Residual history for comparison Test 3.

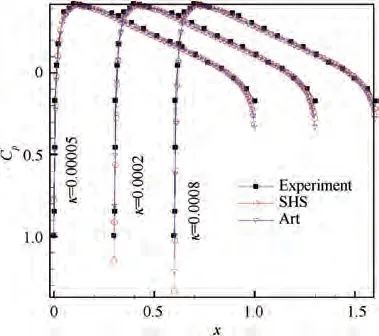
Fig. 27 Pressure distribution for comparison Test 3.

The low speed flow is close to incompressible flow, so the accuracy of density field is usually not considered. SHS method can obtain the correct density field via selecting an appropriate way to change density. We compare flow fields of original equations, precondition method and SHS method,using both density and pressure contours, as shown in Fig. 28.

In Fig. 28, it can be seen that both density and pressure of original equations are wrong, and precondition method gives correct pressure but the quality of density depends on variables used, while SHS method gives correct density and pressure.The relevant mechanism needs further study.

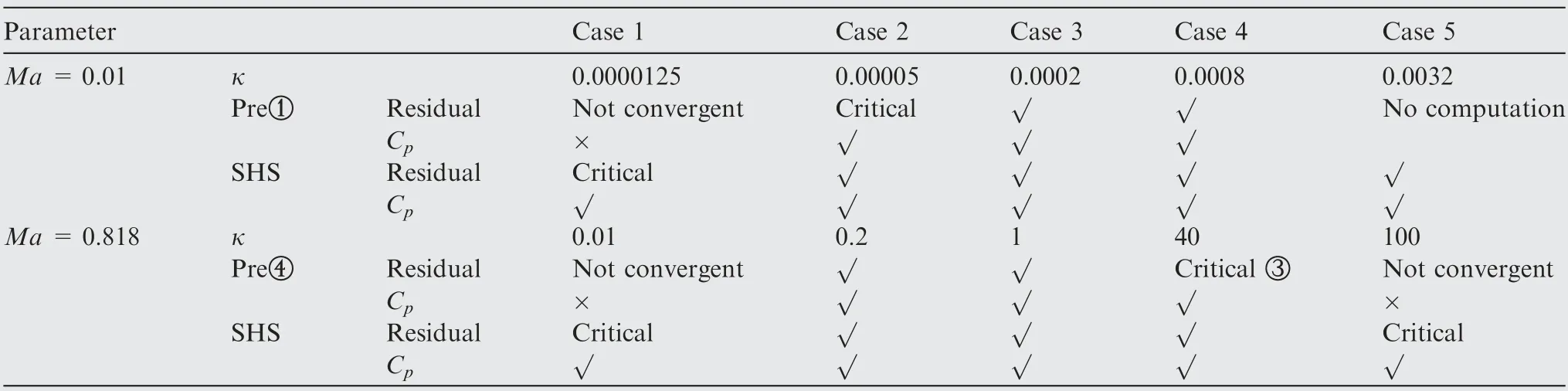
Table 4 Comparisons of SHS and precondition method with different κ for Comparison Test 1 and Comparison Test 2.

6.5. Error comparisons

In order to compare efficiency accurately and fairly,we use the error between numerical solution and exact solution. The ’exact’ solution is obtained using a very fine grid. The tests still use NACA0012, zero angle of attack, Ma=0.01. Numerical solutions use a coarse grid of 169×41, ’exact’ solution uses a fine grid of 1513×361 and is solved via the multi-grid method for speeding up convergence. Fig. 29 displays the ’exact’ grid around the airfoil. Fig. 30 gives the pressure fields of ’exact’solution (black line) and numerical solution (color cloud).Fig. 31 and Fig. 32 are error history and residual history of the four methods.

After selecting the converged errors, residuals and CPU times,we can make a comparison as Table 5 where,CPU time 1 means CPU time consumed when error is converged where the log curve of error becomes flat, and CPU time 2 means CPU time consumed when the computation stops at iteration step 300. From Figs. 31-32 and Table 5, we can see that error converges earlier than residual, and when the error is converged, it is futile for the residual to continue to decline. The error of Art is lower than the error of Precondition, and the error of SHS is the lowest one. The CUP time consumed between Art and SHS are almost the same.The conserved Precondition costs more CPU time because it involves more matrix operations.On the whole,the highest efficiency belongs to SHS, the new method of the present work.

6.6. Analysis of mechanism

Different from the analysis given by Ref.,we give an analysis from another perspective. We think the reason of accuracy problem for low speed flow is mainly that the numerical solution does not converge to the correct one,because Euler equations can have multi-solutions due to its nonlinearity.This can happen when the solution of equations is not unique.For simplicity,the following analysis is made using 1D equations.The existing literatures mention that convergence and accuracy are two separate problems, and give scale comparisons between convective and numerical dissipation terms(it should be noted the comparisons depend on difference schemes). Except the two problems, sensitiveness or robustness of numerical schemes should be considered.Now,we make analysis toward the three problems(uniqueness of solutions,magnitude orders of numerical dissipations and sensitiveness of schemes).

6.6.1. Analysis of uniqueness

In functional analysis, there are three kinds of convergence,strong convergence, weak convergence, weak * convergence.In pseudo time methods, strong convergence means that solution is converged, weak convergence means that residual is converged, weak * convergence means grid convergence.According to functional analysis, the uniqueness of solution is equivalent to solution convergence, while residual convergence in pseudo time iterations is weak convergence, which does not guarantee solution convergence. The necessary and sufficient condition of solution convergence is that the Jacobian of flux has no zero eigenvalue, namely, the Jacobian determinant is non-zero. In 1D case, it is written as

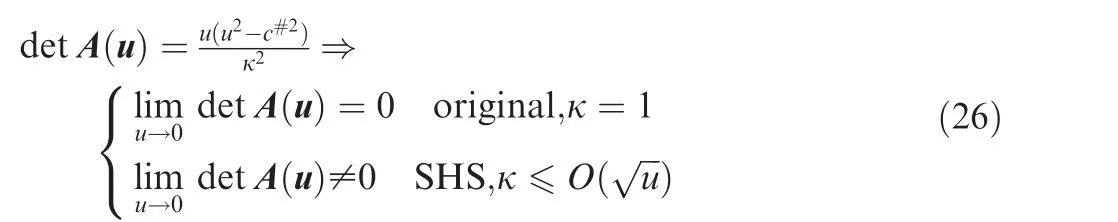
where A(u) is the Jacobian matrix of flux, cis true speed of sound. It can be seen that, for original equations, A(u) is not invertible in the zero limit of low speed,and thus cannot guarantee the uniqueness of the solution. However, for SHS method,as long as κ≤O(u),the singularity of A(u)is avoided to ensure the uniqueness of the solution.It can be summarized as follows:

(1) Residual convergence can only guarantee that the difference equations are satisfied, namely, weak convergence.Decreasing the condition number can accelerate the rate of weak convergence, but does not guarantee strong convergence, that is, the convergence is not guaranteed to be correct.This can explain why sometimes the residual is converged but the result is not correct.

(2) For original equations, the low speed flow differs from stagnation points and sonic lines of high speed flow in that: in low speed flow, detA(u) approaches 0 in entire computational domains, and so the uniqueness cannot be guaranteed ; in high speed flow, detA(u) approaches 0 only in stagnation points and sonic lines which have lower dimensions than the entire computational domain,namely, the volume(Lebesgue measure) of singularity area is 0, and then the uniqueness can be guaranteed as long as entropy condition is satisfied.This can explain why the transonic flow fields do not suffer the crisis of mis-convergence.

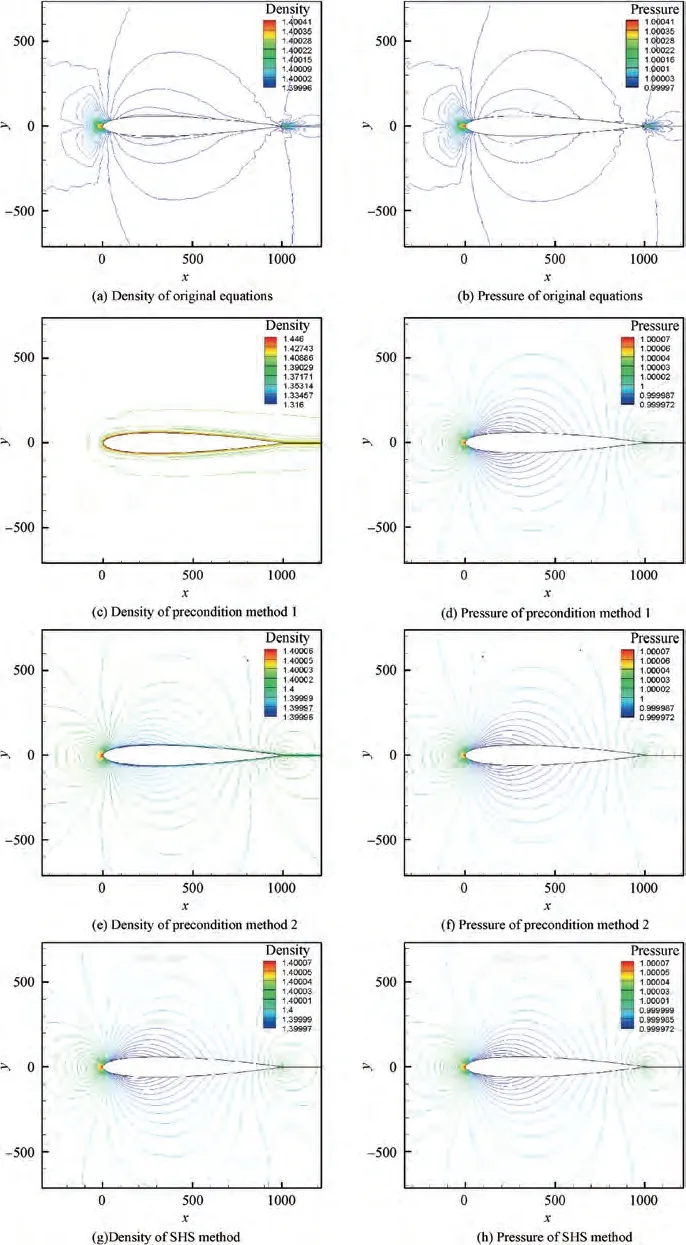
Fig. 28 Density and pressure contours of original equation, precondition with primitive variables, precondition with conservative variables and SHS method (NACA0012, Ma∞=0.01, ρ∞=1.4, p∞=1, κ=0.0002).

Fig. 29 ‘Exact’ grid of 1513×361.

Fig. 30 Pressure: black line-’exact’, cloud-numerical.

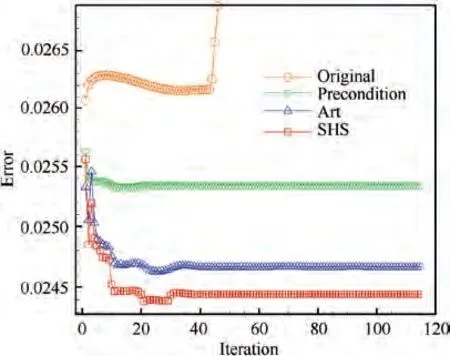
Fig. 31 Error history.

(3) For SHS method, A(u) is non-singular, except for the stagnation points and sonic lines, so the uniqueness can be guaranteed. This can explain why SHS method works normal for all speed flow.

Note: Lebesgue measure is the volume of a region of ndimensional space, and the measure of any lower dimensional area is zero.

6.6.2. Analysis of magnitude order when Ma →0

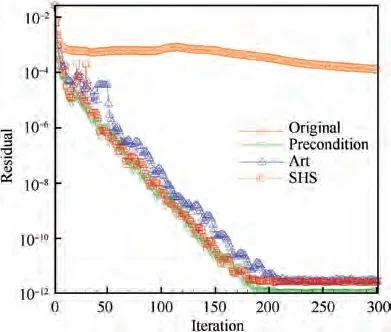
Fig. 32 Residual history.

Numerical dissipation influences the solutions in two ways:(A)it pollutes the solutions when it is excessive;(B)it cannot guarantee entropy condition when it is lacking. For schemes satisfying entropy condition, the (A) is the main agent responsible for accuracy problem.According to the way used by Liu et al.we make analysis of magnitude order using two schemes: (A)Lax scheme; (B) first order upwind scheme with flux vector splitting. Supposing the sound speed is O(1), then Ma →0 is equivalent to u →0, for simplicity, the following analysis is based on flow speed u.

Analysis 1. SHS method can also obtain correct convergence using Lax scheme which is simple and satisfies entropy condition. Since the scheme is easy for analyzing, we use it as an example to make the magnitude order analysis as flow speed approaching zero. Lax scheme and its modified equations in steady case are

where ρ=ρ/κ is true density.For original equations,the magnitude order of second component of numerical dissipation is greater than the corresponding one of convective term, so the excess of numerical dissipation may pollute the solutions.For SHS method, as long as κ ≤O(u), all the magnitude of components of numerical dissipation is less than the ones of convective term,and so the accuracy order can be maintained.

Analysis 2. SHS method can obtain correct convergence using upwind schemes. In order to avoid complicated matrix operations,the upwind scheme with flux vector splitting is usedto analyze the order of magnitude.Rewrite the flux in the form of a linear combination of eigenvalues,that is f(u)=f(u),and in 1D steady case,the first order upwind scheme with flux vector splitting and its modified equations can be written as

Table 5 Comparison of error, residual, and CPU time.

From Eq.(32)it can be seen that,using upwind scheme,for original equations, the magnitude order of numerical dissipation dose not match with the convective term, while for SHS method the magnitude orders of numerical dissipation and convective term are matched. SHS method with both Lax scheme and upwind scheme can get correct convergence, and upwind scheme matches better than Lax scheme, so it is more accurate. In short, the order of magnitude of numerical dissipation is different for different scheme.However,the essential reason of wrong convergence is the non-uniqueness of solution in the limit of zero speed.

6.6.3. Analysis of sensitiveness

The sensitiveness here mainly refers to the parameter sensitivity of matrix involved in the numerical method. The Lax scheme does not use any matrix, there is no such sensitiveness problem. However, the upwind schemes involve matrix of eigenvectors,and the singularity of the matrix should be investigated, which can be observed from the determinant of the matrix L

where L is the matrix of left eigenvector. When |detL(u)|→0,the condition number of L approaches infinity.So, L is singular when κ=0, while for SHS method κ=Ma, which can avoid the singularity.

In short, the accuracy problem from round-off and cancellation can be alleviated by using more accurate precision of computer data in addition to lowering sensitiveness and discrepancy of magnitude order. Slow convergence can be improved through implicit schemes or large time step schemesin addition to lowering the condition number. But the uniqueness problem is guaranteed by increasing pseudo Mach number.

6.7.Comparisons of Precondition,artificial speed of sound,SHS

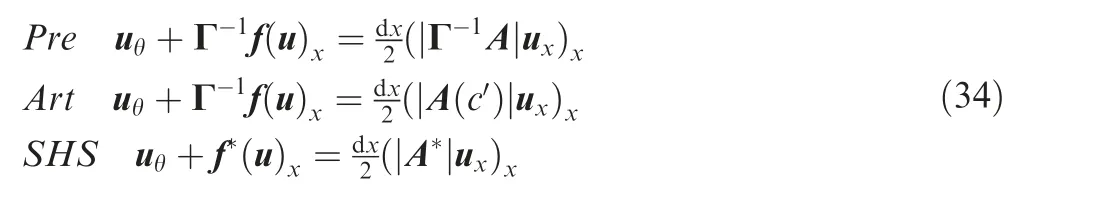
Precondition method is the earliest algorithm for simulating low speed flow using compressible equations. The method of artificial speed of sound can be regarded as a simplified version of precondition method, namely, the numerical dissipation term uses the absolute value of Jacobian of original equations with the sound speed replaced by the pseudo one given by precondition method. Pseudo high speed method increases the pseudo Mach number by transforming conserved variables.The modified equations of Roe scheme of the three methods are compared as follows:where c’ is the artificial sound speed, see the formula (D8) in Appendix D, f*(u) is the flux with ρ replaced by ρ/κ in the way as Eq. (7) or Eq. (10). The advantage of Art method is simplicity, since the eigenvectors in Precondition method are complicated and different for various preconditioner, while the Art method only needs to apply the eigenvectors (with the modified sound speed) of original equations, which is easy to be extended to complex flows. Additionally, Peles and Turkelsaid that the Art method is more robust,and the reason may be that the original eigenvectors contain no sensitive parameters.The advantage of SHS method is the completeness in mathematics which makes it using any high order schemes of original equations easily. The comparisons of Art and SHS are given in Figs. 26-27.

7. Conclusions

From the comparisons, we get conclusions: the convergence rate does have a good negative correlation with the condition number, while the accuracy of computations has a good positive correlation with the pseudo Mach number.From the analysis we get conclusions:the accuracy problem has something to do with numerical dissipations of difference schemes,i.e.,good accuracy can be achieved via matching dissipation as pointed out by many authors in literatures.

The main difference between SHS and precondition method lies in their different construction ideas. SHS method is constructed based on the idea of increasing pseudo Mach number,and it does not pursuit low condition numbers. But the study of precondition method also benefits a great deal to the present work, especially for the understanding of the mechanism of our work.

To summarize, SHS method has the following advantages: (A) no preconditioning matrix; (B) simple formula,easy to code and to extend to more complex flow; (C) keep fully conservation law formulas and be convenient to employ the well developed high resolution and high order schemes; (D) numerical experiments show that it has almost the same convergence rate and accuracy as precondition method; (E) it provides a new idea for study of ill-posed problems.

Additional studies of SHS method include extensions to implicit method and turbulent flows. Furthermore, unsteady flows with dual time step method will also be tested and compared with more up to date precondition methods or other modified methods.

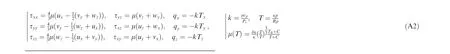
Appendix A. SHS Navier-Stokes equations.

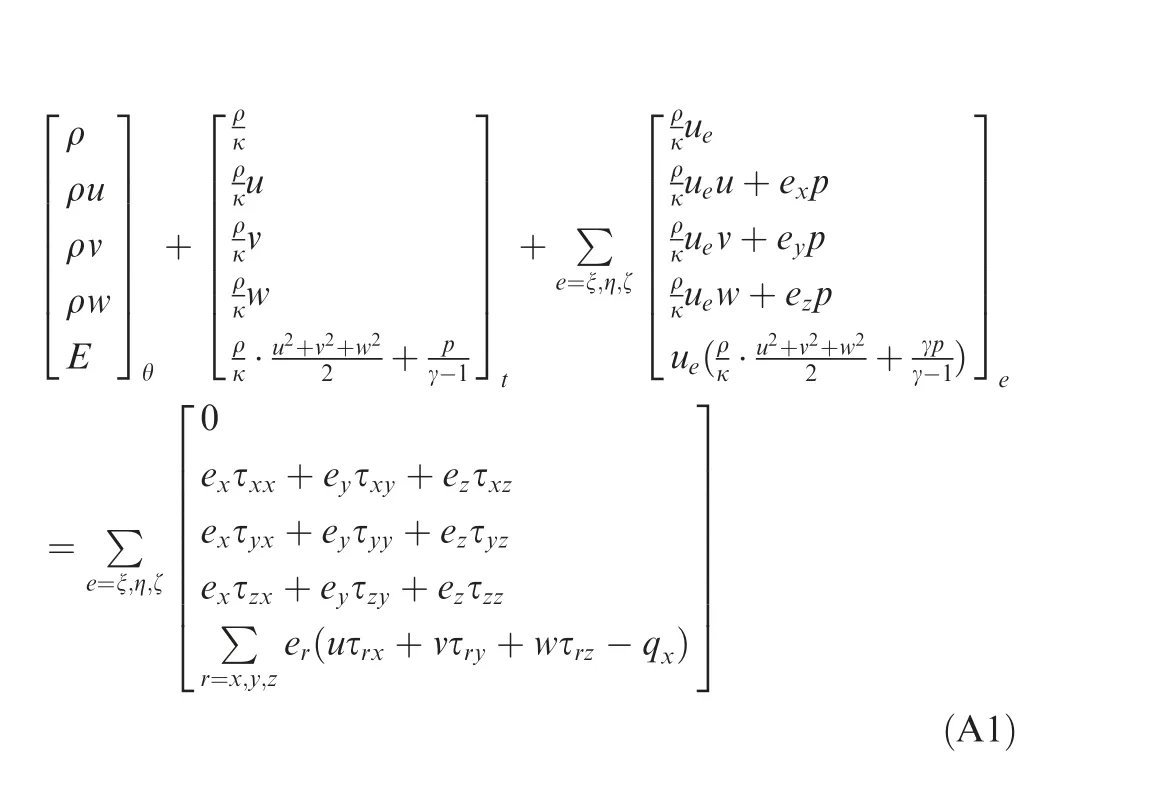
where C=110.4, Pr=0.71, R is gas constant.

Appendix B. The last two rows of left eigenvectors in Eq. (13).

Numerical schemes used in present paper for artificial speed of soundare the same as Appendix C. except that their eigenvalues and eigenvectors are substituted by following:

Note that, the preconditioner is taken from diagonal preconditioning method of Choi and Merkle.

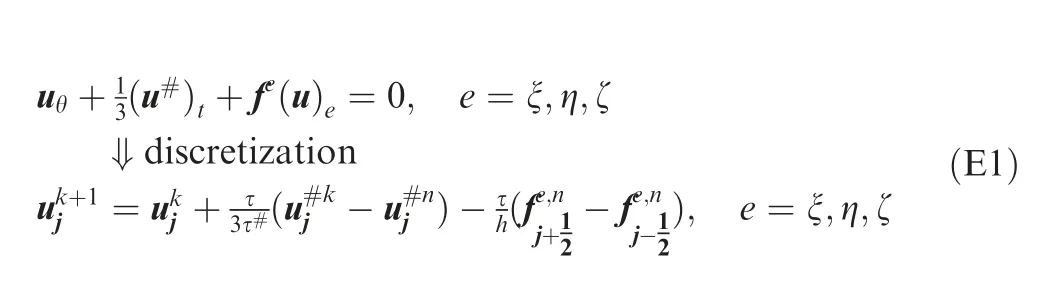
where uare variables in physical time derivative term (·)of Eq.(10),τis physical time step size,τ is pseudo time step size,the superscript n is physical time number, the superscript k is pseudo time number(iteration number). Others are same as the note below Eq.(17). An implicit version of discretization is the following splitting implicit scheme57

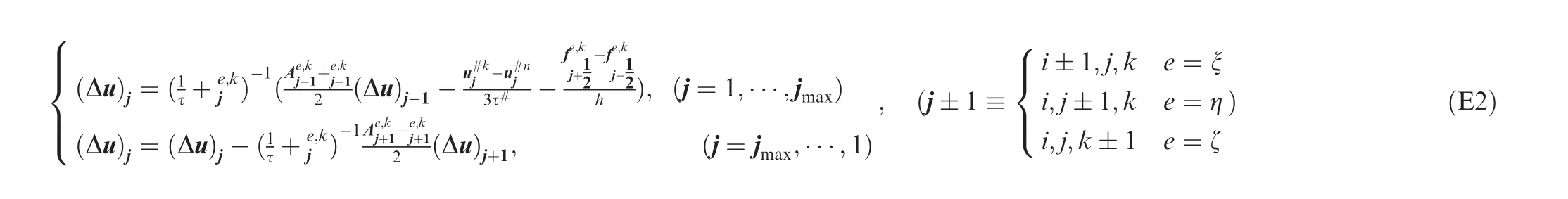
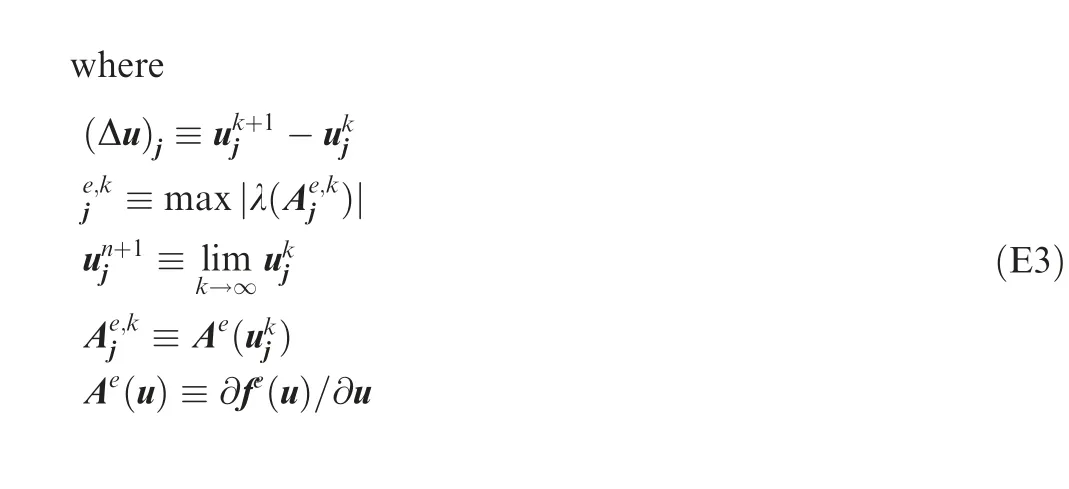
Formula (E2) for SHS is a slightly revised version of the previous workof authors.