Dynamics modeling and error analysis for antenna pointing mechanisms with frictional spatial revolute joints on SE(3)

Long LI, Shengnan LYU, Xilun DING

School of Mechanical Engineering and Automation, Beihang University, Beijing 100083, China

KEYWORDS LCP;Lie-group integration;Mechanism error analysis;Non-smooth dynamics;Spatial revolute joints

Abstract This paper presents a non-smooth multibody dynamic formulation and error analysis of an antenna pointing mechanism including frictional spatial revolute joints(FSRJs)with small clearance in the framework of the special Euclidian group SE(3). The formulation leads to an inertial frame-invariant, a compact and unified description for rigid bodies and spatial revolute joints(SRJs). The geometric constraint of the bearing is covered by four open semi-cylinders, which can be treated as bilateral constraints assuming that the impact effects are negligible.The frictional contact problem is formulated as a horizontal linear complementary problem (HLCP), which is embedded in the Lie-group integration scheme. Error of the antenna pointing mechanism is modeled by means of the adjoint transformation and POE-based formula. The evolution of errors is obtained through the solution of non-smooth dynamics. The obtained numerical results illustrate the influences of FSRJs in dynamics modeling and error analysis of the antenna pointing mechanism.

1. Introduction

The dual-axis antenna pointing mechanisms(DAPMs)play an important role in achieving real-time tracking and precise pointing on target satellites, which have been widely applied in communication satellites and data relay satellites.The kinematic accuracy of the mechanism in an antenna system is a critical factor that restricts the efficiency of the satellite communication system. In practice, the joints in antenna pointing mechanisms are well-made, in which the clearances are small but inevitable, liquid lubrication should be avoided in the microgravity environment. In consequence, it is a challenge and actual problem to achieve a high enough pointing accuracy,especially in space environments.In the general dynamic analysis of multibody mechanical systems,the clearance effects are usually neglected, that is, mechanical joints are assumed ideal or perfect. However, the clearances and friction effects in mechanism degrade the performance of the satellite antenna system and have a significant impact on the position accuracy in on-orbit operation.

A number of studies have been devoted to multibody systems with imperfect joints over the last few decades.Flores et al. gave valuable contributions to dynamics of mechanical system with imperfect kinematic pairs,in their works,regularized approaches are developed to model revolute,translational and spherical clearance joints.Tan et al.studied the planar mechanical system with two revolute clearance joints using the continuous analysis method.Li et al. conducted a comparative study on dynamic response of a planar slider-crank mechanism with two clearance joints and link flexibility.Liu et al.proposed a new contact model for the FEM model of revolute joint, which is suitable for calculating the contact stiffness in the case of small clearance.Based on the proposed contact model,an method for analyzing the effects of joint on dynamic responses of space deployable structure is presented.Li et al.developed a virtual experimental modal analysis method to deal with the joint clearance and link flexibility;they also analyzed the dynamic characteristics of space deployable structure.All aforementioned studies are based on the continuous or regularized approach utilizing the modified Coulomb friction models, which can avoid numerical difficulties but exhibit poor ability to model the static friction and to capture the stick-slip motion.

An alternative method, referred to as non-smooth dynamics formulation, in which the Coulomb dry friction model is adopted, has been studied by many researchers.Glocker and Studer analyzed the contact under dry friction,and formulated the conditions of stick-slip transitions and the contact problem as LCP.Following their study,Flores et al.applied the non-smooth dynamics method to model rigid multibody systems with translational clearance joints, in which the clearance is represented by the normal gap function.On this basis,Zhuang and Wang presented a modeling method for the planar multibody systems with frictional translational joints, the translational joints with small clearance are treated as bilateral constraints by ignoring the impact effect,the complementarity conditions on normal contact forces are established instead of using the normal gap function.Recently, their method is extended to revolute joints with clearance, by employing the Hertzian-based contact force model. The proposed method can evaluate the static friction in the revolute clearance joints.The utility of methods developed for planar multibody systems is somewhat restricted because they are not valid for spatial mechanisms but the real revolute joints may exhibit 3-D motion due to clearance. Therefore, proper modeling of SRJs with clearances in multibody systems is required to predict the dynamic performance of the spatial mechanisms.

The models of SRJs with clearance are much more complicated than the planar case, in which several different possible configurations between the journal and bearing can take place.Flores et al.developed a methodology for assessing the spatial revolute joints with clearances for dynamic analysis of multibody systems based on a continuous contact force model.In the framework of the finite element method, Bauchau and Rodriguez developed a formulation of models for spatial revolute joints with clearance in flexible MBS.Based on previous research, they proposed a method for the analysis of unilateral contact conditions and the resulting friction forces.Brutti et al. proposed a computer-aided model of a 3D revolute joint, which is modeled by introducing a nonlinear equivalent force constraint, without considering the friction effects.Qi et al. proposed a recursive formulation for multibody systems with frictional cylindrical joints with small clearances. The effects of impacts are neglected and locations and forces of contacts in joints can be obtained by the interactions between rigid bodies.In Virlez et al.work,a new 3D cylindrical joint model is developed, which accounts for the clearance and the friction effect.Tian et al. proposed a new model for dry/lubricated cylindrical joint with clearance based on ANCF and NCF formulation,which has been applied to the dynamics in a spatial rigid-flexible MBS.Yan et al.proposed a comprehensive model for 3D revolute joints, in which both radial and axial clearances are considered.Recently, Marques et al.presented an enhanced formulation to model spatial revolute joints with radial and axial clearances in multibody systems.Akhadkar et al.modeled the 3D revolute joints with clearances within the framework of non-smooth mechanics based on an event-capturing time-stepping scheme. Cavalieri and Cardona proposed a new method for modeling the spatial revolute joints with clearance,the non-smooth generalized-alpha scheme is used to deal with the dynamics of multibody systems subjected to frictionless contacts and impacts.

In the aspect of error modeling and analysis, a large number of researchers have studied the error modeling and analysis for both planar and spatial mechanisms by assuming the motion of revolute joint with clearance restricted to the plane which is perpendicular to the rotation axis.However, the real revolute joints with clearance may present out-of-plane motion. Dhande and Chakraborty analyzed the effect on the output error of spatial mechanisms assuming that random clearances are normally distributed.Venanzi and Parenti-Castelli presented a method to evaluating clearance influence on the planar and spatial mechanisms.Zhao et al. proposed a generalized approach of error space calculation for parallel/hybrid manipulators resulting from joint clearance;closed-form formulas for error propagation on motion groups were developed.Li et al.proposed a novel POE-based robot kinematic calibration algorithm based on the axis configuration space and the Adjoint error model.Lin et al. presented a 3D clearance model of the paired bearing support joint; and analyzed the influence of joint clearance on the accuracy of the spatial multi-loop mechanism.

Dynamics modeling for spatial multibody systems and geometric integration on Lie group exhibit advantages regarding singularity-free formulation and numerical implementation.Therefore, there has been an increased interest in studying the rigid/flexible multibody dynamics using Lie group.To authors’ knowledge, little research has been developed to model FSRJs based on non-smooth modeling approaches in Lie group setting. Few researchers have investigated the static friction in SRJs with clearances utilizing the Coulomb dry friction model.Meanwhile, no studies have been conducted on error calculation of spatial mechanisms based on the nonsmooth dynamics analysis.

The main contribution of this paper is summarized as follows. Based on our previous work,a novel modeling approach is presented to simulate the FSRJs with small clearances for non-smooth dynamics of MBS on SE(3). The dynamic modeling of a dual-axis antenna pointing mechanisms based on the HLCP is performed. Error analyzing method of DAPMs based on the Adjoint error model is developed by utilizing the non-smooth dynamics approach. The proposed formulation can describe all possible different scenarios of FSRJs in a unified manner and deal with frictional contact problem without modifying the Coulomb’s friction law. The contact status can be detected and the stick-slip motion can be simulated easily based on the normal and tangential complementarity conditions. The evolution of errors in DAPMs could be obtained by the solution of non-smooth dynamics.

In this work,we are interested in non-colliding but multiple frictional contact problems of SRJ with small clearance in antenna pointing mechanisms. In Sec.2, the geometric and kinematic model of spatial revolute joints with small clearances is presented. In Sec.3, the complementarity conditions of the normal and tangential contact forces in FSRJs are established respectively. In Sec.4, the dynamic equations of multibody systems with FSRJs are formulated based on HLCP in Lie group setting. In Sec.5, the error analysis of the antenna pointing mechanism is performed by employing the Adjoint error model.

2. System modeling

2.1. Description of the system

The mechanical system is a cylindrical satellite body equipped with a DAPM consisting of two links connected with FSRJs.The structure and coordinate frames of DAPM are shown in Fig. 1.

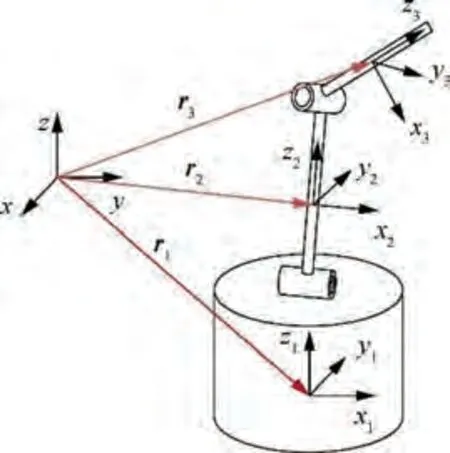
Fig. 1 Model of satellite with DAPM.

2.2. Kinematics of FSRJs

The FSRJ is composed of two rigid cylindrical bodies, i.e.,journal and bearing. There are two actual cases for the model of SRJC, depending on the lengths of journal and bearing, by reason that the normal forces are always perpendicular to the longer joint element. The formulation proposed is applicable in either case, without loss of generality, the case that the length of bearing is longer than that of the journal is considered in this paper.

Assumption 1. The size of clearance considered in this paper is small so that the geometric constraint of FSRJs can be treated as bilateral constraints by neglecting the impact between the joint elements.

Note that the dynamic response of mechanisms with small clearance joints closes to the ideal response by the reason of a small number of impacts in joints take place.Hence, the impact effect is ignorable in the present work.

Assumption 2. The radial dimension of the journal is small enough compared to the axial dimension so that the journal cannot be in contact with the flanges of both sides of the bearing simultaneously.

Under the assumptions above, it is reasonable to consider that the contact between the journal and the flange of the bearing can be considered as surface-to-surface contact, and the resultant force of the axial constraint is through the mass center of the journal. In consequence, the torque caused by the axial constraint is zero.

In the SE(3) formalism, the left-invariant representation of the tangent vector is convenient for kinematics and dynamics modeling, due to the invariance with respect to the choice of the inertial frame. In this study, all the general velocity will be expressed in its body-fixed frame in this paper. Hence, the relative configuration between two rigid bodies A and B which are connected by a revolute joint can be expressed as

G=GG（2）

where Gand Gdenotes the configuration of the rigid body A and B respectively, Gdescribes the relative configuration between body A and B.

The tangent map induced by the left translation on Liegroup relates the tangent space of SE(3)at a certain configuration to its Lie-algebra. Given a left-invariant vector field,which can be obtained by a linear isomorphism from the tangent space at identity to the tangent space at configuration G,the tangent vector ˙G at an arbitrary point on SE(3) can be associated with an element of Lie algebra by

where,pis the relative displacement between the origins of the journal frame Σand the bearing frame Σ,Rdenotes the attitude of the journal axis in frame Σ, eis the base vector in z direction of frame Σ,eand eare the base vectors in x and y directions of frame Σ.

2.3. Kinematics of the DAPM

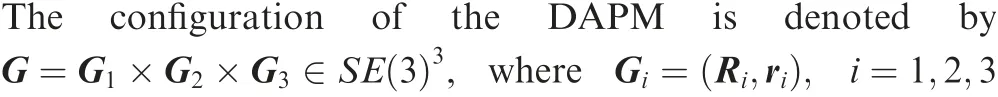
Fig. 2 Model of a SRJ with clearances.

3. Complementary formulation

3.1. Preliminaries of LCP

A linear complementarity problem (LCP) can be described as following: For given A ∈Rand b ∈R, find solutions x ∈Rand y ∈Rsubjected to a set of linear equations y=Ax+b and the inequality complementarity conditions 0 ≤y ⊥x ≥0, which can be written as an inclusion

The unilateral primitive and the Sgn-multifunction are maximal monotone set-valued maps which are depicted in Fig. 3.

3.2. Normal contact law

The journal is subjected to rigid motion with respect to the bearing. Fig. 2 shows the schematic of SRJ with clearance,in which the geometric dimensioning is exaggerated for illustration. In respect of the radial clearance, the relative configuration of the SRJ can be described as four possible contact situations between the journal and bearing,which are enumerated as shown in Fig. 4

1) No contact exists between the bearing and journal of the SRJ in the radial direction,i.e.,no reaction force acts on the bearing wall of the SRJ.

2) One point of the journal is in contact with the bearing wall. Meanwhile, only one normal constraining force exists at the contact point of the bearing wall.

3) Two points of the journal are in contact with the bearing, and two constraint forces acting at the two contact points are in two opposite directions.

4) A line contact happens between the journal and the bearing, the constraint force of the line contact equals a resultant force.

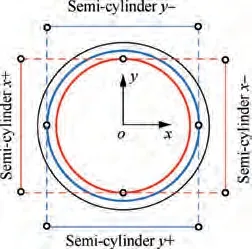
Fig. 5 Schematic of bearing’s open covers.

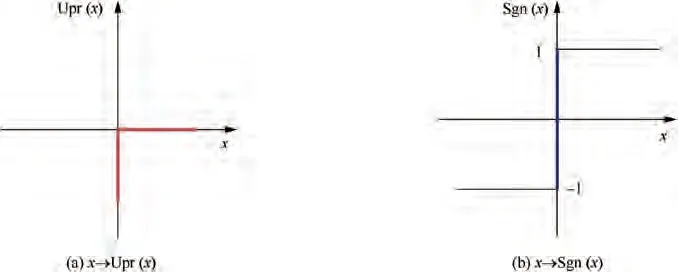
Fig. 3 Graphs of unilateral primitive and Sgn-multifunction.

Fig. 4 Four different possible relative configurations in a SRJ with clearances.

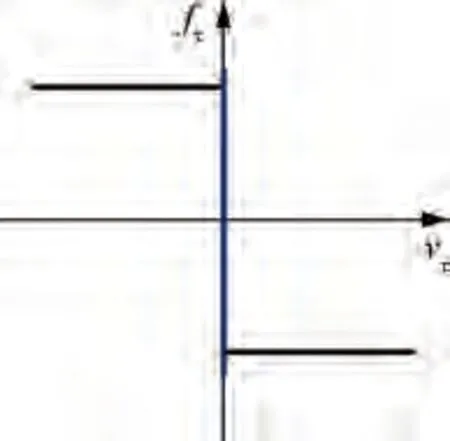
Fig. 6 Coulomb’s friction model.

3.3. Tangential contact law

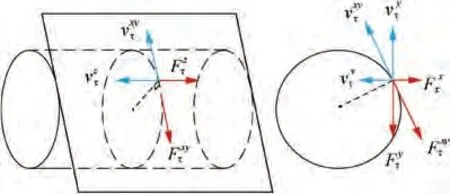
Fig. 7 Relative velocity and corresponding friction force at a certain contact point.

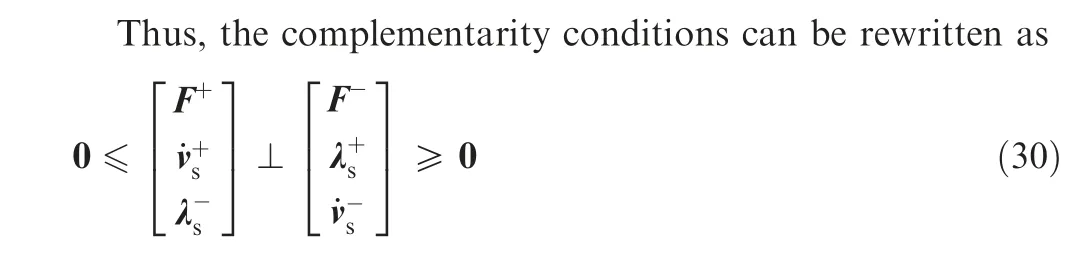
4. Deformation analysis of the PCDM

4.1. Dynamic modeling on SE(3)

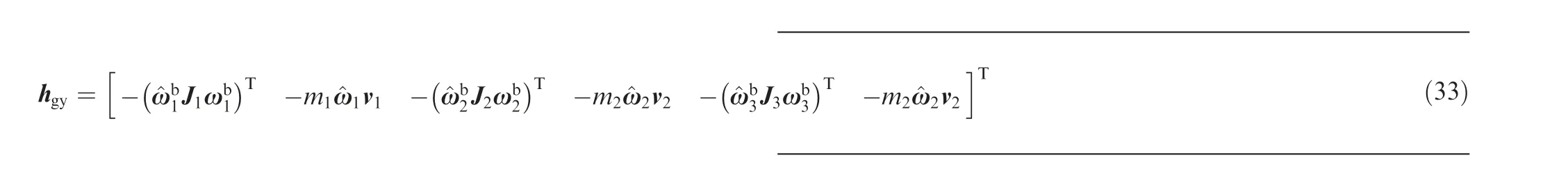
where, τis the driving torque expressed in the bearing frame Σ.

Φ denotes the constraint vector of DAPM, Φis the constraint Jacobian matrix of the system. It can be established by assembling all the articulated constraints and kinematic constraints in the following form

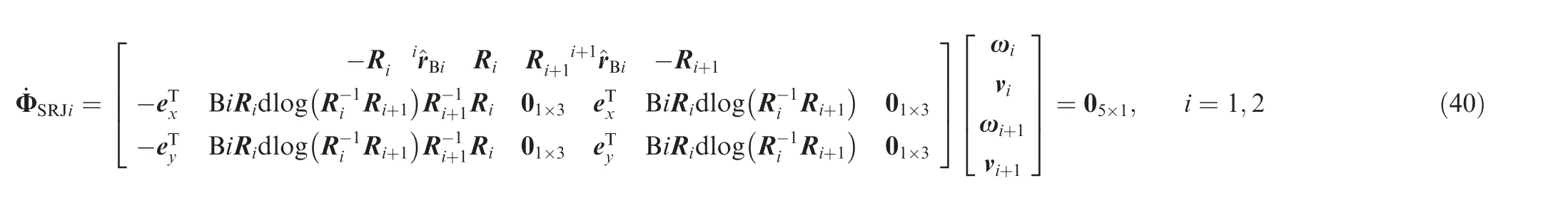
Analogously,the acceleration constraint can be given in the form

The constraint equations can be given by the Baumgarte’s stabilization method

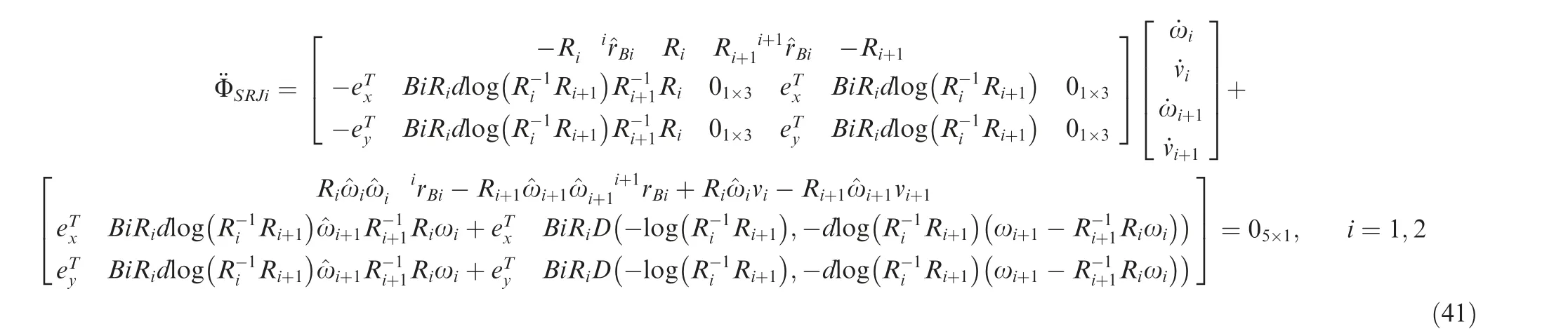
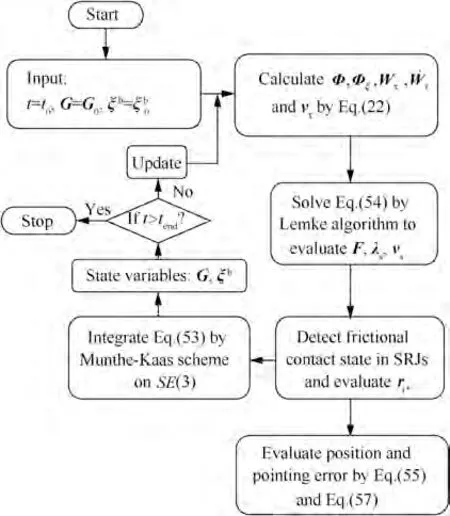
Fig. 8 Computational procedure for multibody systems with FSRJs.

4.2. Integration scheme for HLCP

The frictional contact problem of multibody systems can be solved by a horizontal linear complementarity problem(HLCP), which can be written as

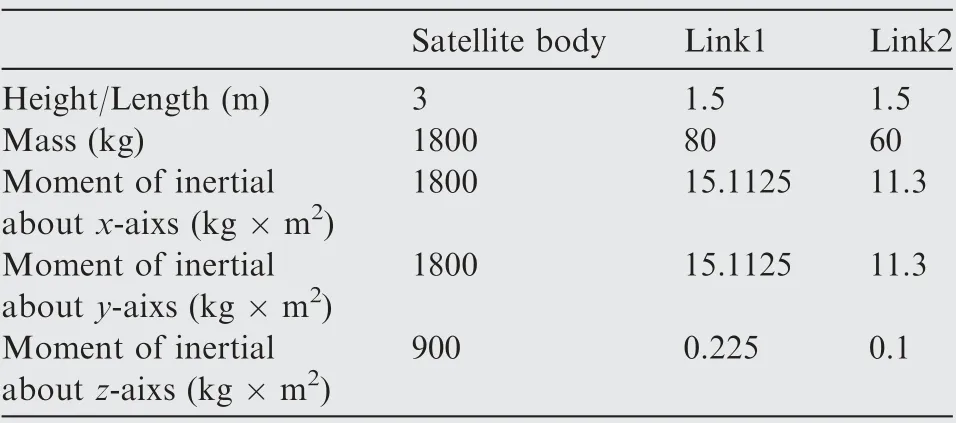
Table 1 Geometric and inertia properties of the DAPM.

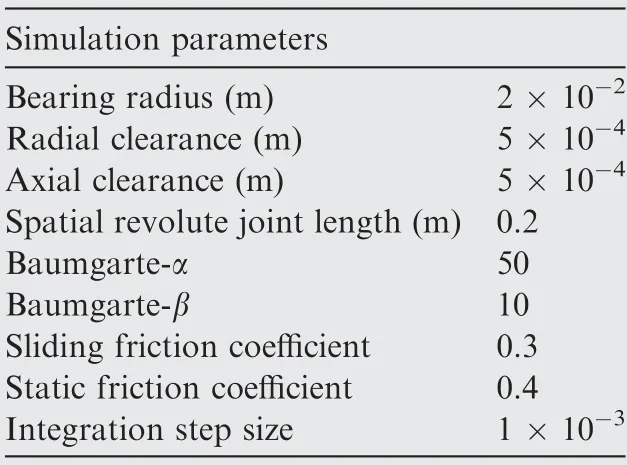
Table 2 Parameters used in the dynamic simulation of DAPM.

Eqs. (30) and (53) can be solved by Lemke’s method. Substituting the obtained results into Eq. (52), the differential equations of motion evolving on SE(3) can be calculated via Lie group integration scheme, such as the Munthe-Kaas algorithm. The proposed computational method for calculating dynamics and evaluating errors is presented in the flowchart in Fig. 8. It is developed in the framework of multibody dynamics on SE(3).

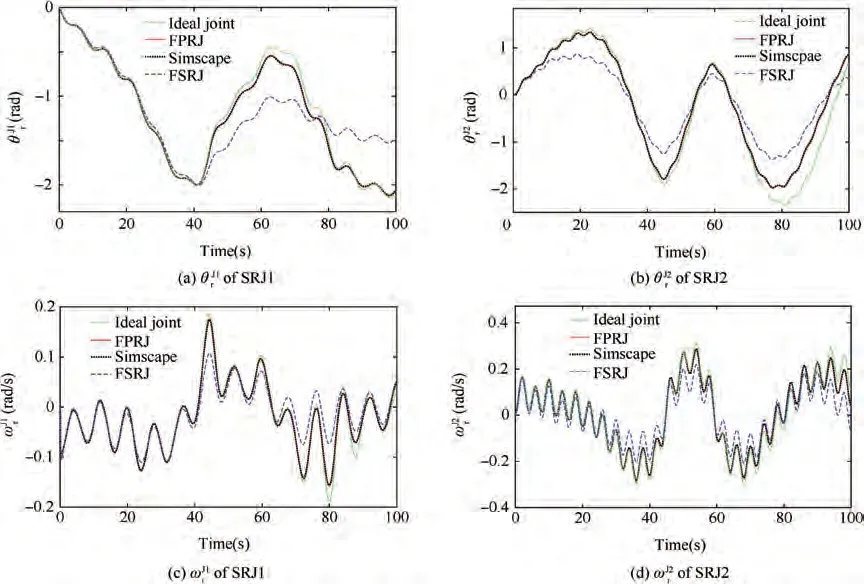
Fig. 9 Kinematics of DAPM with periodic driving.

4.3. Numerical results

The geometric and inertial parameters are given in Table 1.The parameters used in dynamic simulations are listed in Table 2.

In the followings, the numerical tests will be simulated under different driving conditions:

The periodic driving is

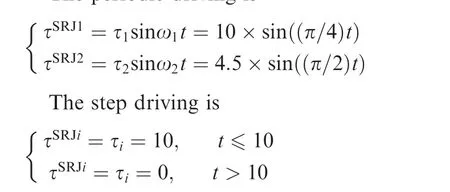
The dynamic response of DAPM is simulated with revolute joints modeled by the following three cases: (1) ideal revolute joint model; (2) frictional planar revolute joint model (FPRJ);(3)frictional spatial revolute joint model.For comparison with the proposed method, the dynamic response of DAPM with FPRJ is simulated in Simscape. The results based on the Coulomb dry friction model is compared with those given by the modified Coulomb friction model. The non-smooth dynamic behavior of the system can be obtained; several numerical results are analyzed to demonstrate the correctness and effectiveness of the presented method.

Fig.9(a-d)depicts the time evolution of the relative angular displacement and angular velocity of SRJ with periodic driving. It can be seen that the motion curves in the case of frictional planar revolute joints given by the propose method almost coincide with those from Simscape, which valid the proposed modelingmethod to a certain extent. The cases of DAPM with ideal revolute joints and FPRJ are special cases of FSRJ with clearance. The simulation results show that the amplitude of motion decreases due to the effect of friction in revolute joints compared with the ideal case; the amplitude of motion in FSRJ is smaller than that in FPRJ. The reason is that the constraint forces in FSRJ are larger than those in FPRJ due to the gyroscopic torque generated by the spatial motion of the DAPM. As a result, the friction forces in FSRJ are larger than those in FPRJ.

Under step driving, the dynamic responses based on the Coulomb dry friction model and the modified Coulomb friction model are shown in Fig.10.Fig.10(a)depicts the velocity magnitude of contact point in SRJ1 and the angular acceleration of link 1 in ×x direction. Fig. 10(c) depicts the velocity magnitude of contact point in SRJ2 and the angular acceleration of link 2 in z direction. Fig. 10(b) and (d) are the magnified view of Fig. 10(a) and (c) respectively. As illustrated in Fig. 10(b), the contact points exhibit stick-slip motion when the Coulomb dry friction model is employed.The acceleration of link 1 has the mutation phenomena when the relative tangential velocity of the contact point is close to zero. (smaller than or equal to 1×10numerically). As shown in Fig. 10(d), the numerical result based on Coulomb friction model is similar with that using the modified Coulomb friction model,by reason that the relative tangential velocity of the contact point is nonzero.

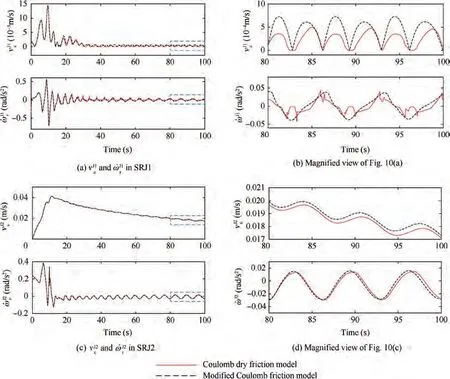
Fig. 10 Kinematics of DAPM with step driving.

5. Error calculation of DAPM

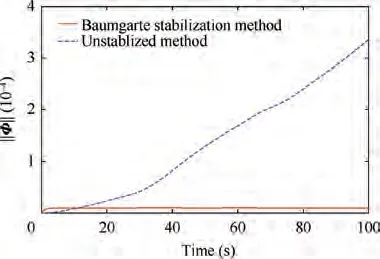
Fig. 11 Drift of constraint equations with and without stabilization.

The deviations of the FSRJs can be described as the rigid displacement of their axis,which is given by the Adjoint action of SE(3)on se(3)naturally.The axis of a spatial revolute joint can be parameterized by twist coordinates. Therefore, the Adjoint error model can be given by the Adjoint transformation,

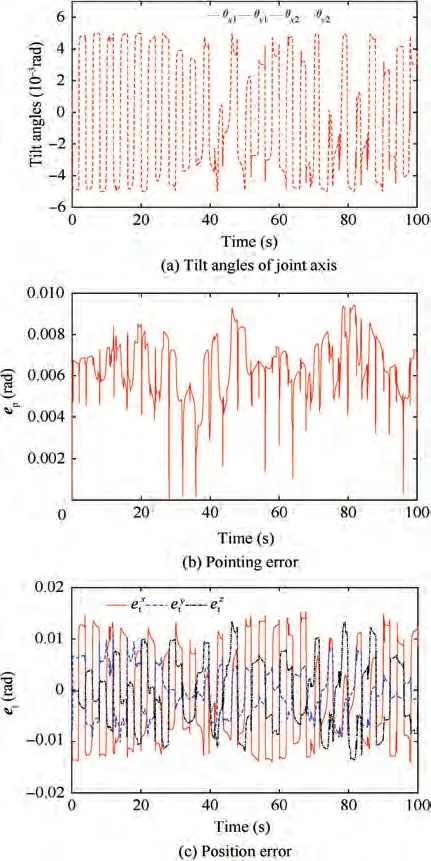
Fig. 12 Evolution of errors of DAPM with periodic driving.

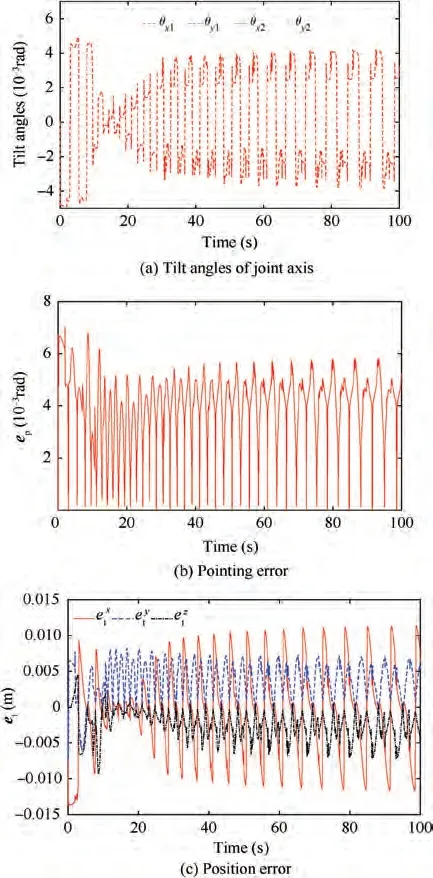
Fig. 13 Evolution of errors of DAPM with step driving.

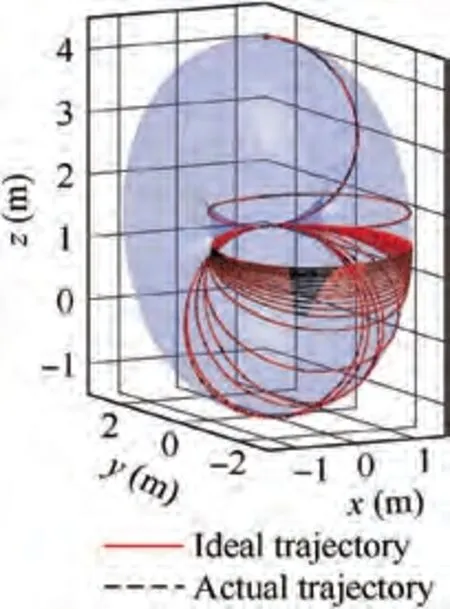
Fig.14 3D view of actual and ideal trajectory of end effector tip.

6. Conclusions

A non-smooth dynamic modeling and error analysis method on SE(3) for DAPM with frictional spatial revolute joints is proposed in the paper.The computational methodology is presented in Lie-group SE(3)framework,which naturally leads to a frame-invariant and singularity-free formulation. On account of the small size of clearance, geometric constraints are treated as bilateral constraints covered by four open semi-cylinders. The normal and tangential complementarity conditions are established to detect the transitions of contact situations and stick-slip transitions. Hence, the contactfriction problem is formulated and solved as a horizontal linear complementary problem (HLCP), which is embedded in the Munthe-Kaas Lie-group integration scheme. Baumgarte’s stabilization method is employed to decrease a numerical constraint drift. The error of DAPM is analyzed by means of the Adjoint error model and POE formula.

The advantages and characteristics of the proposed method are as follows:

(1) Different possible relative configurations between the journal and the bearing can be described in a unified formulation.The current contact situation of FSRJs can be determined by the position of contacting points which can be located by the normal contact forces.

(2) Different from the widely used regularized approach for FSRJs, in which the Coulomb friction model cannot be adopted,the Coulomb dry friction model can be utilized in the presented method to simulate stick-slip motion.

(3) The error model of DAPMs is formulated by adjoint action and POE formula, which can be calculated by the solution of non-smooth dynamics. Therefore, the evolution of errors can be obtained.

As a conclusion,the proposed non-smooth dynamics modeling and error calculation method for DAPM is based on Lie group SE(3)formulation,which can be numerically solved utilizing Lie group integration scheme. The method can be applied easily to the dynamic modeling and error analysis of general multibody systems with FSRJs.

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

This research has been supported by the National Natural Science Foundation of China (No. 51635002 Key Program,52075016, U20A20281).