改进人工势场的手术机器人位姿规划

郝林佳,叶 灿,都书鲜,王 宇,武 博,张 楠

(首都医科大学生物医学工程学院,北京 100069;首都医科大学临床生物力学应用基础研究北京市重点实验室,北京 100069)

1 引言

近年来,外科手术向着微创化的方向发展,特别是手术机器人在临床中的应用,不仅节省了手术时间,减轻了医生工作量,同时也提高了手术精度,并将对患者的损伤减少到最小,给医生和患者均带来了较大益处.另一方面,由于机器人执行手术,它处理对象的特性与工业应用的情况有较大差异,因此要求手术机器人具有十分细致、柔顺的操作性能以及安全的应急系统.对于术中执行手术的机械臂而言,需要避免机械臂末端执行器以及各连杆与器械等运动对象发生碰撞乃至接触,以免干预手术的进行,影响手术精度.

目前为止,国内外对手术机器人的研究基本都是主从式控制,避免了外界物体对机器人路径的干扰问题,如国外的达芬奇系统[1]、Magellan手术系统[2]以及国内的妙手机器人[3]、神经外科机器人Remebot[4]等.面向未来非主从式医疗机器人研发,避障变得尤为重要.本研究以工业机器人为起点提出一种位姿规划算法,解决了手术机器人的安全避障问题.

常用的机械臂避障算法主要包括改进逆运动学求解法[5–6]、自由空间法[7]、遗传算法[8]、A*算法[9]等,其中:逆运动学求解法无法有效解决奇异点问题;自由空间法无法适用于空间冗余机械臂;A*算法和遗传算法均为搜索算法,耗时长.另外也有学者提出基于自适应权重的优化方法[10]以及基于预测窗的避障避碰算法[11],兼顾了机器人的避障和运动的平稳性,但前者是在关节空间内进行规划,而后者针对的是移动机器人,因此在本文的场景中并不适用.

人工势场法[12]是一种高效的局部路径规划算法,其基本思想是在机器人工作空间或执行空间构建虚拟势场,在目标点设置作用于全局的引力场,在障碍物设置作用于局部范围的斥力场,机器人在两场的共同作用下到达目标并避开沿途障碍.它结构简单,运用方便,可重复性强,在动态避障以及目标追踪方面应用较为广泛.由于是局部路径规划算法,因此也容易出现局部极小值问题.

为了解决局部极小值问题,不少学者引入虚拟目标点[13–16],在极小值附近添加虚拟障碍物[17]或者在和速度的法方向添加加速度[18],其中文献[13–16]所提算法对于障碍物最近距离的计算不准确,同时需要进行搜索和遍历,耗时长;文献[17–18]中的算法虽然可以进行动态避障和跟踪,但是需要计算伪逆矩阵,不能很好地解决奇异值问题.并且除文献[13,16]外,上述算法针对的是对末端执行器位置的规划,并没有考虑姿态.而文献[13,16]提出的算法虽然可以规划姿态,但其需要事先计算机械臂目标位置的各关节角,而冗余机械臂的运动学逆解又会涉及最优解、奇异值等问题,对于动态障碍物而言,事先规划的关节位置可能并不安全.

为此本文提出改进人工势场的手术机器人位姿规划算法,首先将末端执行器两端位置信息作用于引力函数中,解决了传统人工势场算法不能约束姿态的问题;接着在避障方面,相对于其它方法,通过GJK算法计算凸体障碍物与机械臂之间的实时距离[19]会更加准确,提高了避障精度;然后,将末端执行器目标位姿与当前位姿之间的差距作为自适应步长中的变量,让机械臂运动更加平缓高效;最后,在机械臂陷入局部极小值时,引入动态引力常数,使机械臂逃离局部最优,以应对手术场景的多种情况.

2 环境建模

2.1 运动学模型

本文采用德国库卡公司的LBR iiwa 7七自由度冗余机械臂作为研究对象,加入末端执行器后如图1所示,采用标准D–H法建立机械臂运动学模型,可得该机械臂的标准D–H模型参数,如表1所示,机械臂正运动学模型可用式(1)表示为

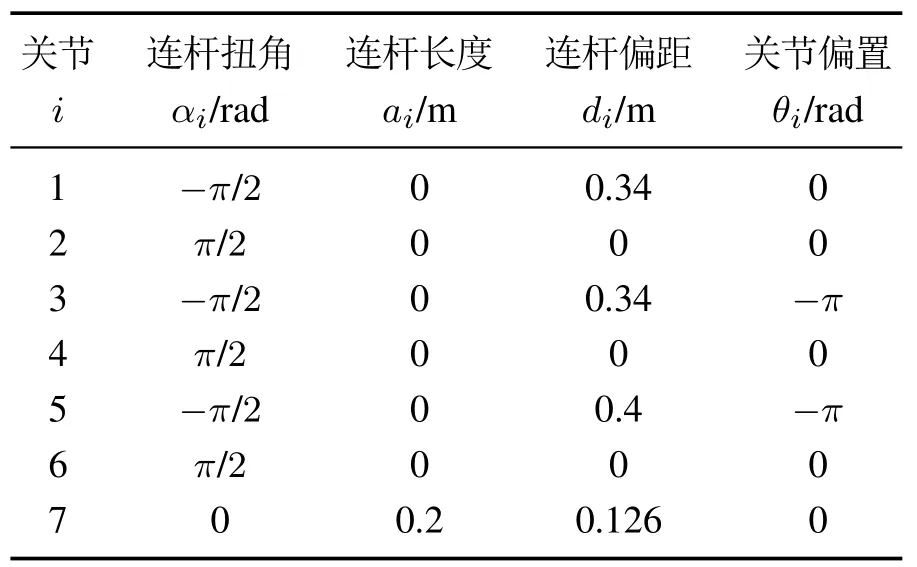
表1 机械臂D–H模型参数Table 1 The D–H parameter of the robot

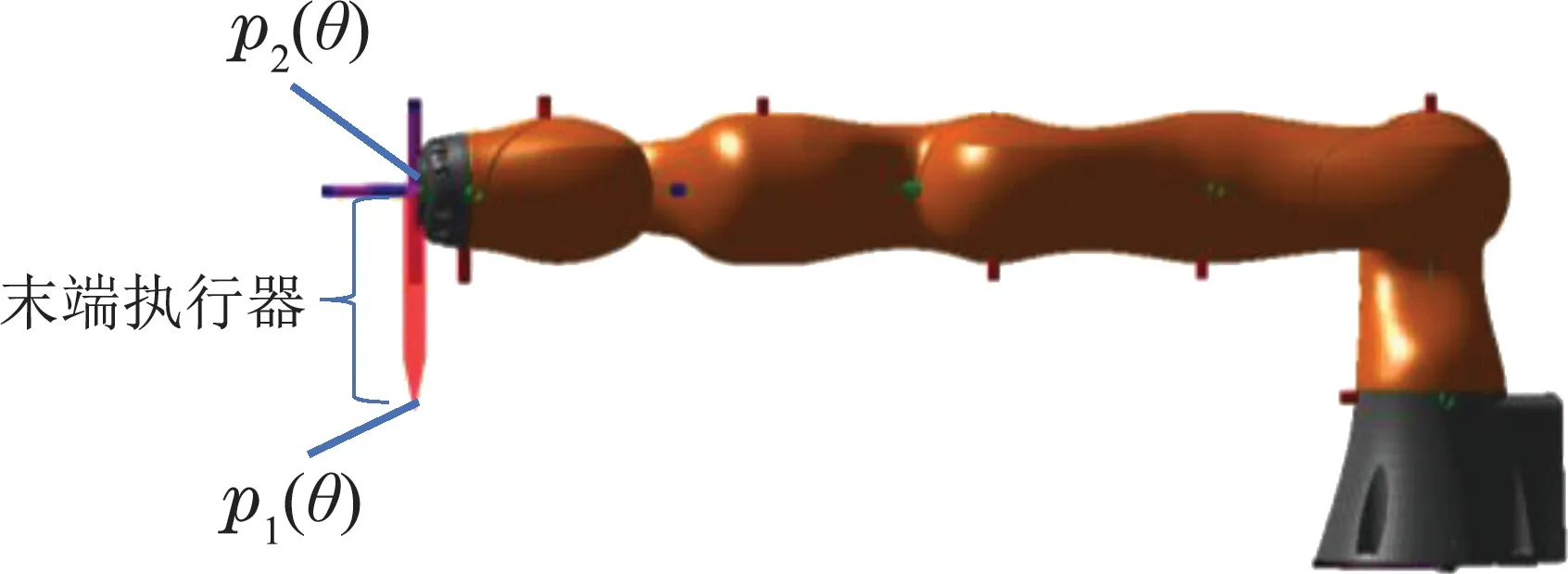
图1 库卡LBR iiwa 7七自由度冗余机械臂Fig.1 KUKA LBR iiwa 7 7-DOF redundant robot

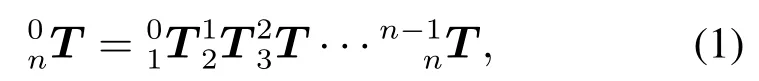
式中n表示机械臂关节数,表示相邻连杆坐标系之间的变换矩阵,带入标准D–H模型参数便可得机械臂末端在工作空间中相对世界坐标系的位姿.

机器人学中,需要研究机器人末端执行器速度和关节速度之间的映射关系,而反映两者之间的关系的变换矩阵称为雅可比矩阵,用式(2)表示为

式中:=[vxvyvzωxωyωz]T,[vxvyvz]为机械臂末端笛卡尔线速度,[ωxωyωz]为机械臂末端笛卡尔角速度;J(θ)∈R6×n为雅克比矩阵,代表机械臂各个关节速度.雅可比矩阵不仅揭示了速度之间的关系,还表示了力的传递关系,同时为关节力矩的确定以及不同坐标系之间的速度,加速度的变换提供了计算上的方便.

2.2 障碍物模型

由于机械臂的工作环境不同,有的机械臂面对的是提前规划好的规则障碍物,例如工业机械臂,然而更多的时候,机械臂运行环境中的障碍物都是不规则形状,想要精确建模需要花费大量时间,例如球体,AABB,OBB,k-Dops[20]等包围盒.但上述的建模的方法会在很大程度上增大障碍物的体积,从而导致机械臂的工作空间减小,因此本文采用快速凸包算法[21]尽可能少的增大障碍物的体积,保证工作空间的同时不会过多影响机械臂的实时控制,如图2所示.

图2 障碍物凸体化过程Fig.2 The process of bulging obstacles

算法核心包括两方面:一方面是初始点的选取;另一方面是凸点的计算.

选取的初始点有3个,首先根据障碍物的顶点数据,选取z坐标最大的顶点pa(xa,ya,za),计算pa与剩下所有顶点在水平面的夹角θx,θy,使θx,θy最小的两个点pb(xb,yb,zb),pc(xc,yc,zc)与pa共同组成平面f1.θx,θy用式(3)表示为

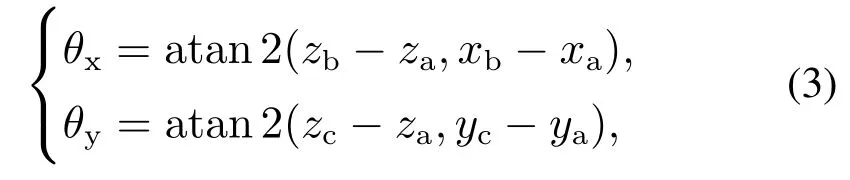
atan 2(x,y)定义如式(4)所示:

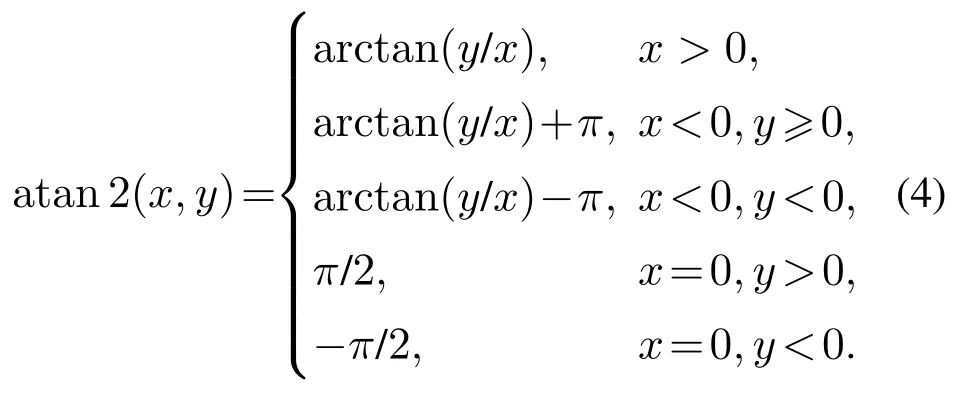
接着遍历剩余顶点,与初始顶点中的任意两点组成新的平面f2,计算平面f1与平面f2的夹角,将使θf最大的面中的3个顶点重排序后作为新的初始点,以此类推,直到找出所有凸点.两平面的夹角可用式(5)表示:

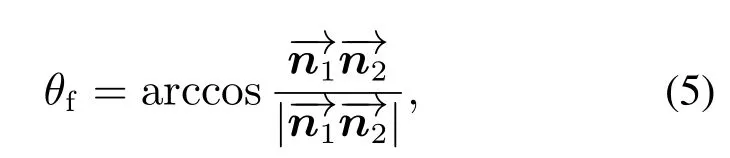
2.3 碰撞检测模型

机械臂与障碍物间的碰撞检测采用GJK算法,根据图1建立的机械臂D–H模型,将连杆等效为以5条线段为轴线的等效圆柱面,图3(a)为连杆等效圆柱面示意图,pi(xi,yi,zi)为第i个关节的坐标,可由正运动学计算求出,ri为等效半径,则等效圆柱面可用方程(6)表示为

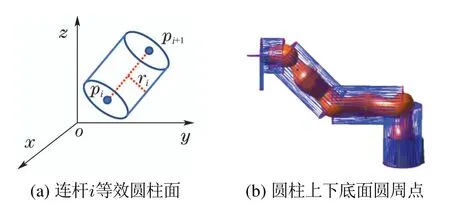
图3 机械臂各连杆等效圆柱面Fig.3 The equivalent cylinders of links of the robot

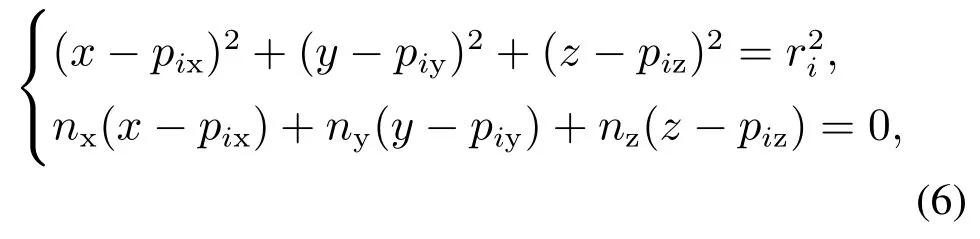
式中:nx=xi+1−xi,ny=yi+1−yi,nz=zi+1−zi,(x,y,z)为机械臂第i个连杆等效圆柱面上点的坐标,(pix,piy,piz)为线段pipi+1中的任意一点,满足:pix=xi+tnx,piy=yi+tny,piz=zi+tnz,0 ≤t≤1.

由于圆柱本身就是凸体,圆柱上下底面圆周上的点就可以代表整个圆柱在空间中的位置,以此减少圆柱面点的个数,如图3(b)所示.

另一方面,障碍物的位置信息由深度相机给出,经过快速凸包算法处理后可以将其当做凸体处理.因此,可以获取任意时刻空间中两个凸体顶点信息.GJK算法的核心思想是将两个凸体的顶点依次相减得到闵科夫斯基差,如果两个物体相交,则闵科夫斯基差将包含原点,否则计算闵科夫斯基差形成的多面体与原点的最近距离以及最近距离点,此距离即为两个凸体之间的最近距离.

需要注意的是,在每次迭代中,方向向量要朝着原点方向迭代,保证单纯形逐渐向原点靠近.以二维凸体为例,用式(7)表示为

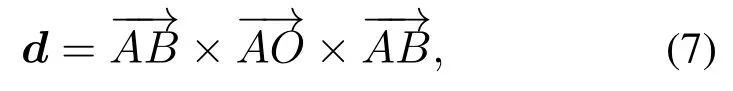
式中:A,B为单纯形中的两点,O为坐标原点.

当单纯形迭代到距离原点最近时,需要根据单纯形中距离原点最近的点E计算出原凸体中对应的最近距离点F,G,它们之间的关系可用方程(8)表示为

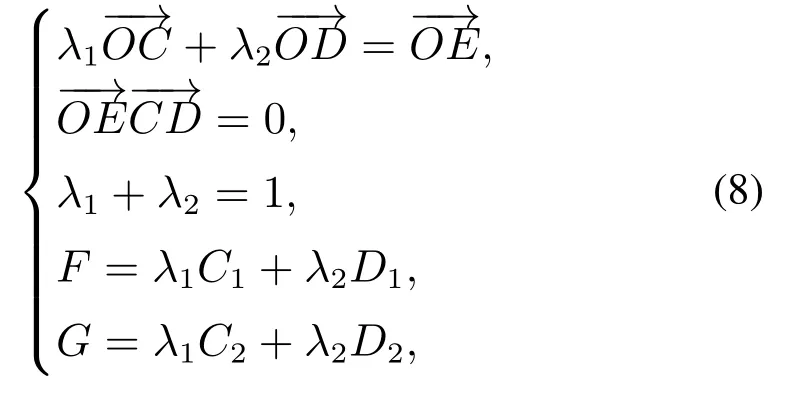
式中:C,D分别为单纯形中距离原点最近的边上的两点,C由凸体1中的点C1减凸体2中的点C2所得,D由凸体1中的点D1减凸体2中的点D2所得,λ1≥0,λ2≥0.

3 改进人工势场算法

3.1 势场函数的建立

由于将障碍物从笛卡尔空间映射到机械臂关节空间计算量大且较难描述,为保证机械臂能在线实时规划,并避开动/静态障碍物,本文直接在笛卡尔空间构造势场模型.考虑到机械臂任务只由其末端执行器执行,并不关心执行任务时其连杆所在位置,而任何情况下都不允许机械臂与障碍物碰撞.因此,吸引力Fatt通过目标在机械臂末端产生,排斥力Frej通过障碍物在机械臂与障碍物的最近距离点处产生,机械臂在两种虚拟力的共同作用下运动,到达目标并避开障碍.需要注意的是,末端执行器是按照规划姿态到达目标位置,传统的人工势场算法只能对末端执行器的位置进行约束,不能兼顾姿态,本文通过对执行器两端的位置分别进行限制,解决了这一问题.

在笛卡尔空间中建立引力势能函数为

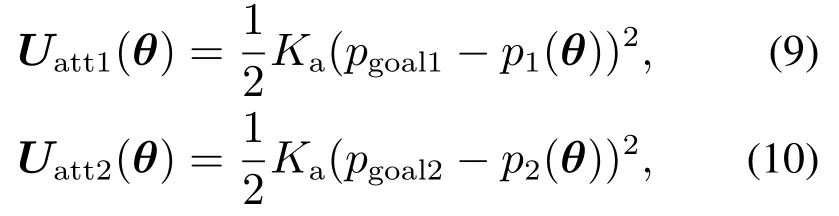
式中:Ka为引力常数,pgoal1,pgoal2为末端执行器两端的目标位置,θ为机械臂运动过程中各关节的角度,p1(θ),p2(θ)为机械臂运动过程中末端执行器两端的实时位置,如图1所示.则对应的引力函数为

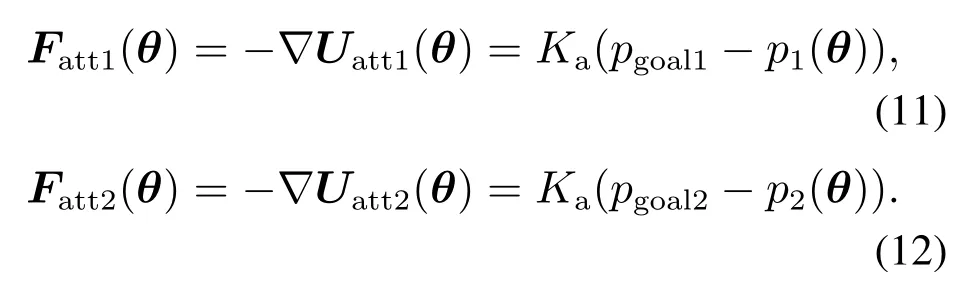
在笛卡尔空间中,障碍物凸包与机械臂连杆等效圆柱面间的斥力势能函数为

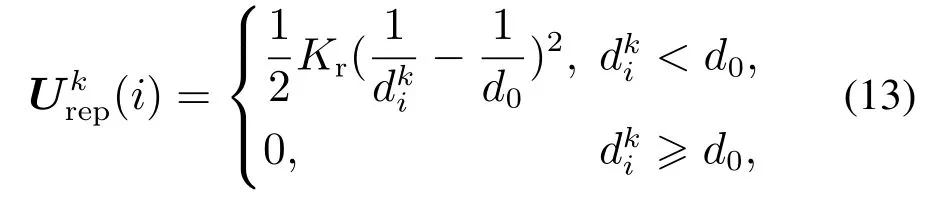
式中:Kr为斥力常数,i(i=1,2,···n)为机械臂连杆序号,k(k=1,2,···m)为障碍物的序号,m为空间中障碍物的总个数,表示连杆i与障碍物k凸包表面的最近距离,d0为斥力势场作用范围,为障碍物k作用于连杆i的斥力势能,它随着的减小而增大,当趋近于d0时,斥力势能迅速增大并趋于无穷,引导机械臂向远离障碍物方向运动.对应的斥力函数为

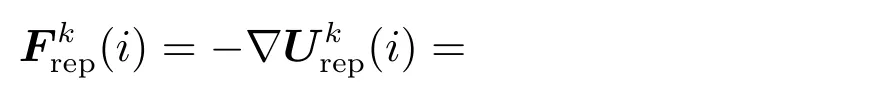
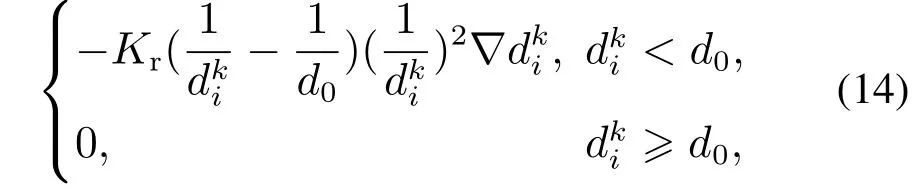
式中:R3为单位向量,方向为连杆i等效圆柱面的最近点指向第k个凸包表面最近点.

3.2 合扭矩的计算

不少学者采用遍历的方式寻找使得总势能最小的关节组合,此方法计算速度很慢,不能表现出良好的实时性,本文则利用势能的负梯度作为力的大小和方向,将人工势场产生的虚拟力作用于机械臂,以此驱动机械臂运动,使得机械臂每一步的运动都是局部最优.接触力F与关节扭矩τ的关系可以表示为

式中:J∈R3×n为接触力作用点处的雅克比矩阵,F∈R3为接触力,此处为人工势场产生的虚拟力,τ∈Rn为接触力作用点产生的各关节扭矩,吸引力作用于机械臂末端执行器两端,用式(16)表示为

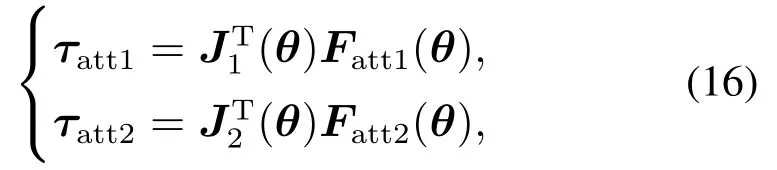
式中:J1(θ)∈R3×n,J2(θ)∈R3×n为机械臂末端执行器两端的雅克比矩阵.排斥力作用于连杆上的最近距离点,用式(17)表示为

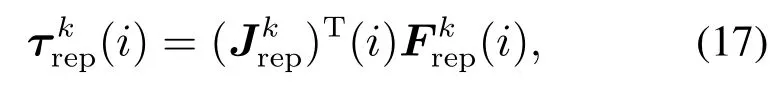
结合引力扭矩以及斥力扭矩,合扭矩τtotal可用式(18)表示为

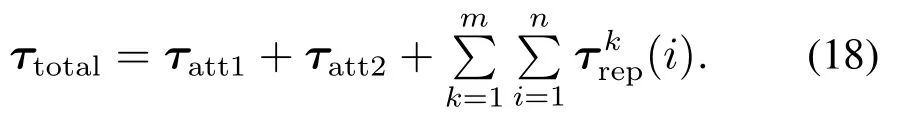
3.3 自适应步长的设计

根据第3.2节合扭矩的计算结果,可以得出机械臂各关节的运动情况,设置每一步的运动步长约束,记为θstep,则下一步各关节的角度可以用式(19)表示为

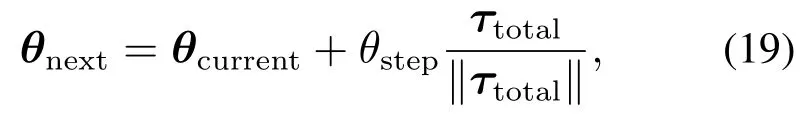
式中:θcurrent∈Rn为机械臂各关节当前角度,θstep∈R+为设置的约束步长,∥∥为二范数计算符,θnext为机械臂运动到下一步时各关节角度.

从式(19)可用看出,机械臂运动幅度不会因为引力或者斥力过大而过大,而是与设置的运动步长相关.为了让机械臂平稳高效地运动,本研究对运动步长做了如下改进,使其随着末端执行器与目标的距离自适应的调整,用式(20)表示为

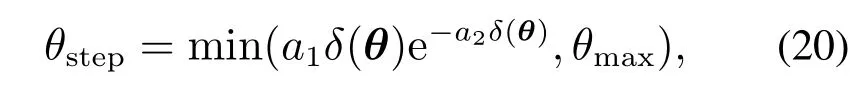
式中:a1,a2,θmax均为正常数,min为取两者之间的较小者操作符,δ(θ)代表机械臂各关节角为θ时,末端执行器两端与目标之间的距离,

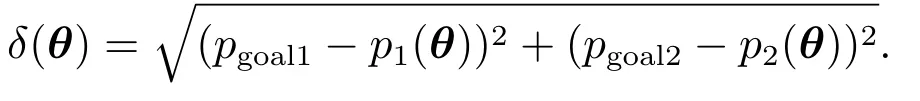
3.4 局部极小值的逃离

当引力势函数与多个斥力势函数共同作用时,总势能容易陷入局部极小而非全局最小值.如果不改变势场分布将难以引导机械臂继续运动,导致避障任务失败.不少研究通过添加虚拟目标或者虚拟障碍物以逃离局部极小值,这两个方法均不适用于本研究在操作空间的位姿规划.针对目标关节角不可知的情况,本研究对引力常数Ka进行改进,使Ka的值随着局部极小值出现的次数r以及预检测碰撞的次数c动态变化,如式(21)所示,从而破坏势场平衡,使机械臂逃离局部极小值.

局部极小值的判定是计算一段时间内末端执行器两端与目标之间误差平均改变量,如果它小于阈值δthreshold则判定为局部极小值.定义如下:

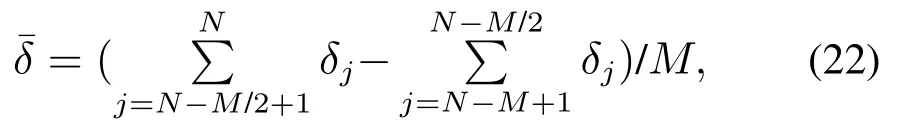
式中:N为机械臂运动的当前时刻,M为检测局部极小值的时间步长,δj代表j时刻末端执行器两端与目标位置的距离,定义如下:

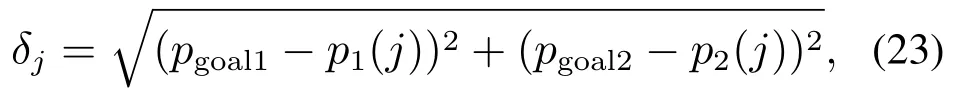
p1(j),p2(j)代表时刻末端执行器两端的位置.

预检测碰撞是指对局部极小值进行处理后,会很大程度上改变势场的分布,此时极有可能导致机械臂与障碍物发生碰撞,因此算法会计算机械臂下一步的运动是否发生碰撞,如果发生碰撞,则根据发生碰撞的次数减小引力常数.

引力常数改变后,势场有很大波动,机械臂末端执行器的状态也会发生一定的改变,因此局部极小值检测会在一段时间内不再进行,待势场稳定后重新检测.

基于改进人工势场的手术机器人位姿规划算法主流程如下:

步骤1获取机械臂当前位姿下的关节角,根据正运动学计算出各关节点在基坐标系下的坐标;

步骤2根据各关节计算机械臂各连杆等效线段以及柱面方程式,同时计算末端执行器两端与目标的距离,确定自适应步长;

步骤3将深度相机捕获的障碍物点云利用快速凸包算法进行凸体化,利用GJK算法计算障碍物与各连杆以及末端执行器之间的最近距离以及最近距离点,由障碍物上最近距离点指向机械臂连杆(末端执行器)上的最近距离点的方向即为斥力势能最快的下降方向;

步骤4计算末端执行器两端的引力以及机械臂连杆(末端执行器)上最近距离点的斥力,获取对应位置的雅克比矩阵,用于合扭矩的计算;

步骤5根据自适应步长以及合扭矩求出机械臂下一步各关节角;

步骤6利用GJK算法检测机械臂在关节角下是否与障碍物发生碰撞,如果碰撞则减小引力常数,返回步骤4,否则进行步骤7;

步骤7检查计数器是否在工作状态(初始化计数器为非工作状态):

如果是非工作状态,判定机械臂是否陷入局部极小:若陷入局部极小,则逐渐增大引力常数以破坏势场平衡,同时启动计数器,在计数期间内停止对局部极小值的检测,进行步骤6,否则进行步骤8;如果是工作状态,则进行步骤8;

步骤8判定末端执行器是否稳定于目标位姿附近,满足条件则停止运动,否则返回步骤1.

4 仿真与测试

为验证本文所设计算法的可行性以及有效性,本节利用MATLAB 2020b模拟实际机器人系统,进行虚拟实物测试,验证机械臂能否避开动态障碍物达到指定位姿.设计的仿真实验包括:不同目标位姿下可达性实验,静态以及动态避障实验,局部极小值实验.

4.1 不同目标位姿下可达性实验

为了验证两点约束法的有效性,本节设计不同位姿下机械臂的可达性实验,δ(θ)<10−4m代表末端执行器到达目标位姿,初始化参数如下:

机械臂初始位姿为θcurrent=[0 0 0 0 0 0 0]T,Ka=106,a1=0.2,a2=0.2,θmax=0.01 rad,十组不同目标位姿如图4所示,目标点为pgoal1,方向为箭头所示由pgoal2指向pgoal1.

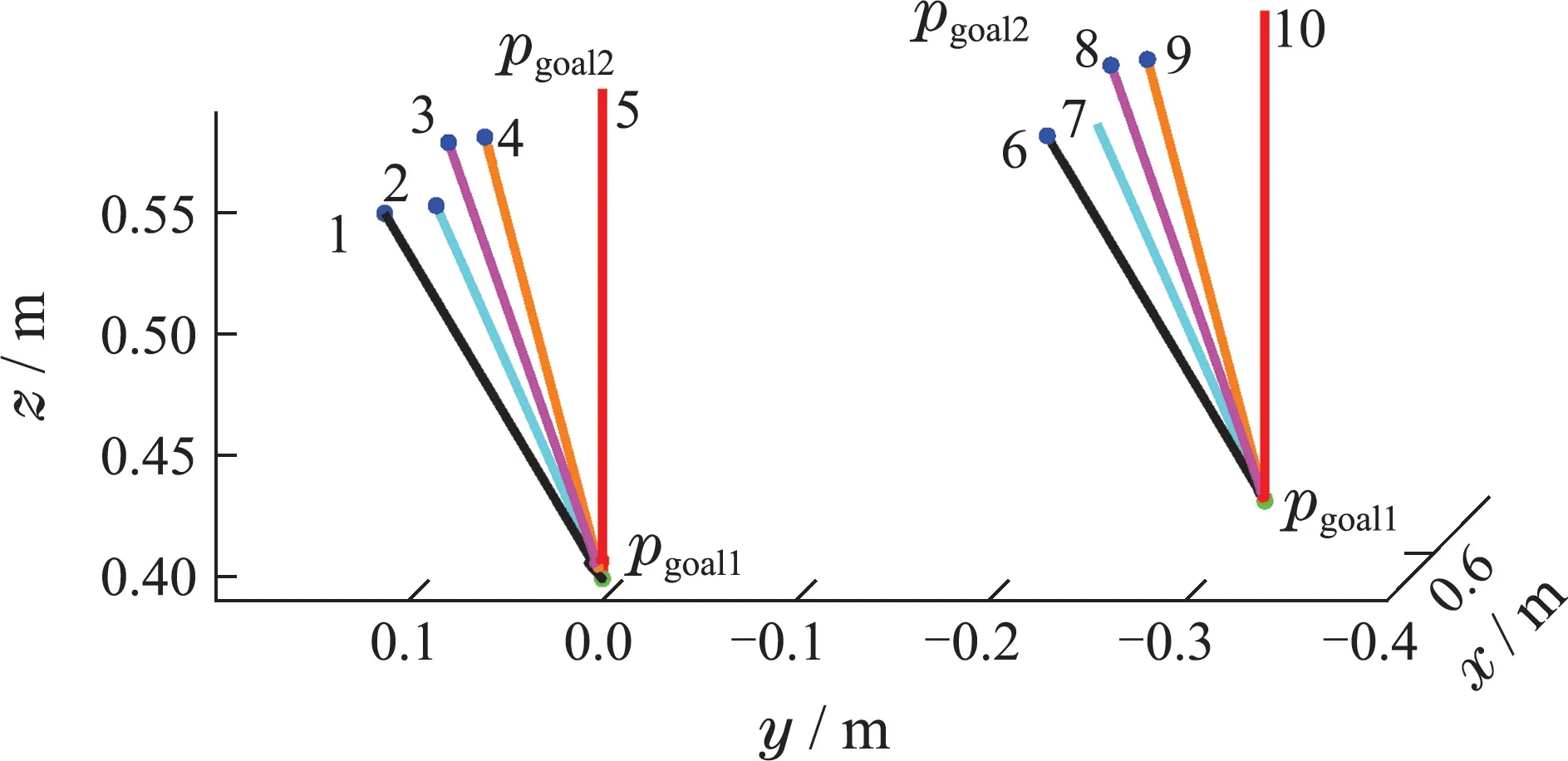
图4 十组目标位姿Fig.4 Ten target poses

表2显示了在不同的目标位姿下,末端执行器都能准确快速的到达.图5为第1组目标位姿下机械臂各关节的运动轨迹,可以看出,机械臂各关节角度变化很小,运动较为平缓.图6为机械臂末端执行器两端与目标之间的位置误差与时间的关系,可以看出,末端执行器在离目标较远时,机械臂运动的幅度较大,随着与目标逐渐靠近,运动逐渐变慢,从而避免了因运动步长过大错过了目标位置或者在目标附近震荡.

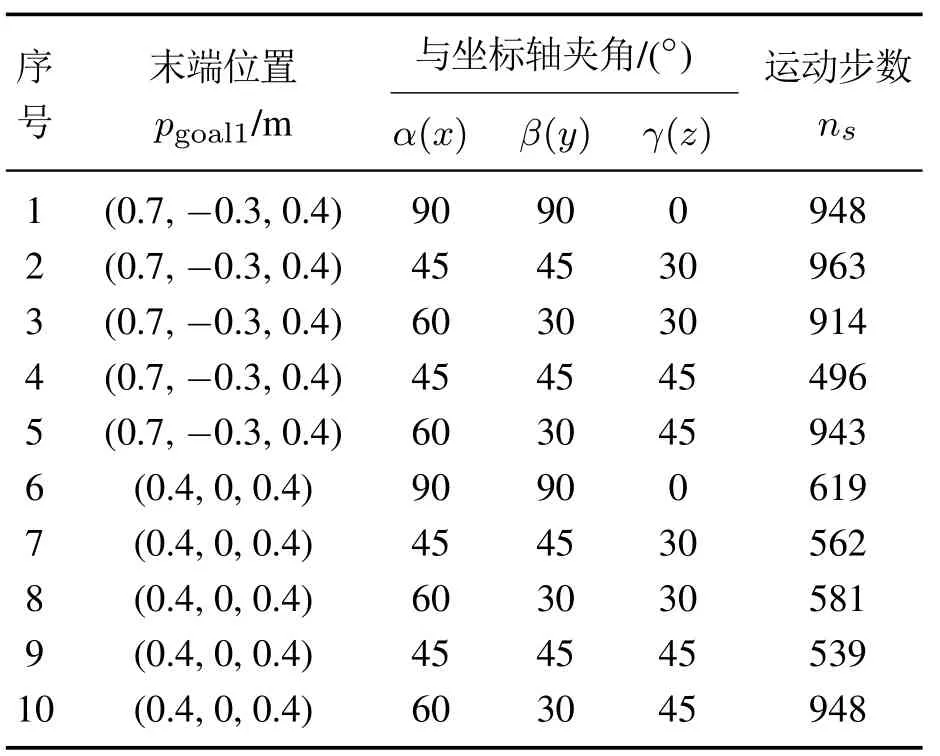
表2 机械臂在不同目标位姿下的运动情况Table 2 The motion of the robot in different target poses

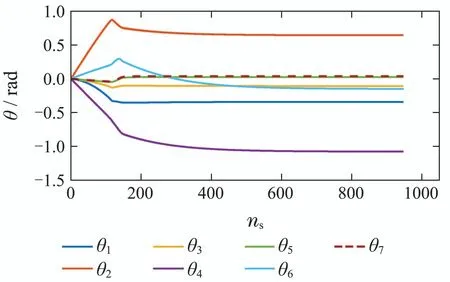
图5 机械臂各关节的运动轨迹Fig.5 The motion trajectory of each joint of the robot

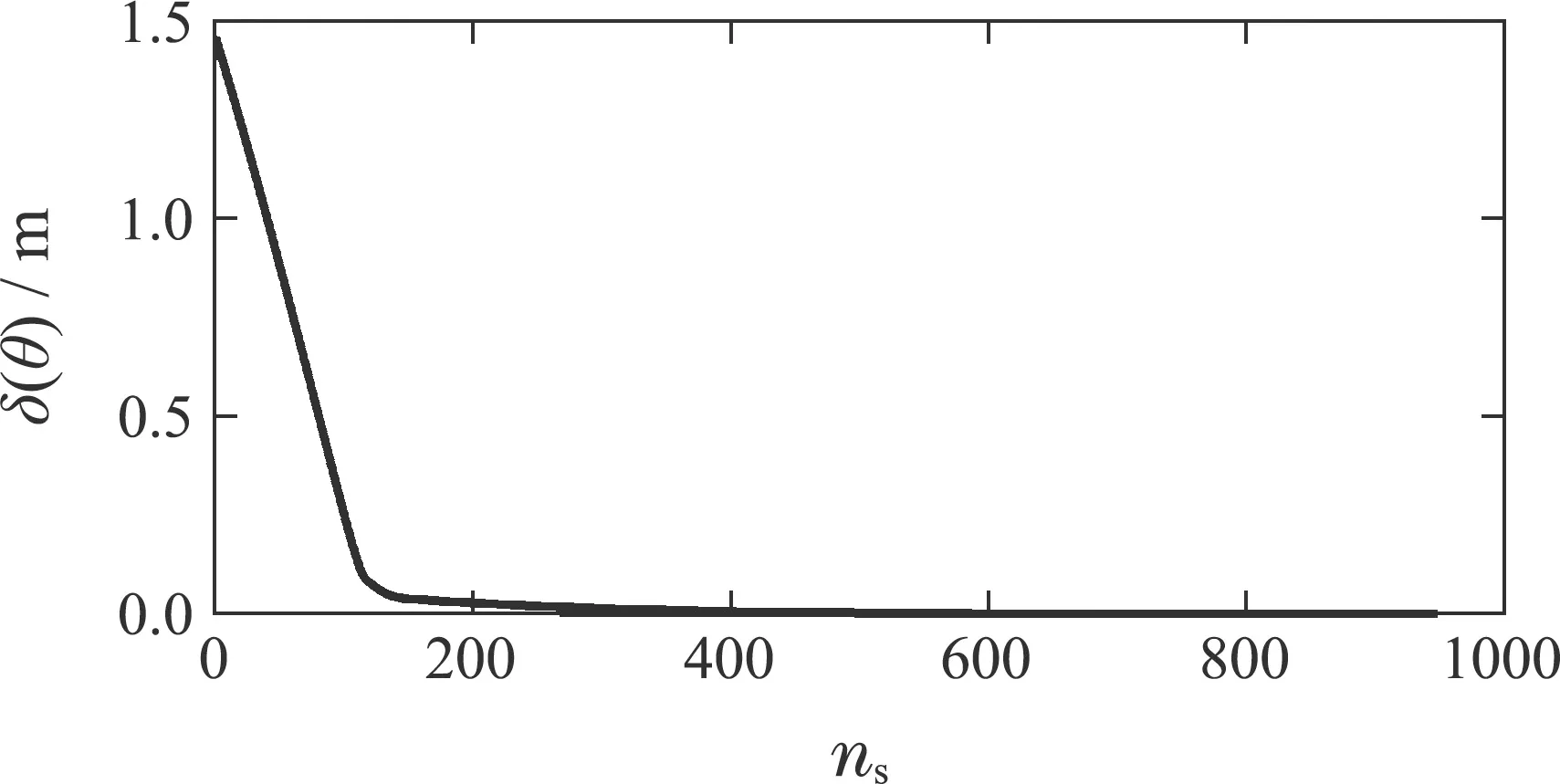
图6 末端执行器两端与目标之间的位置误差Fig.6 Position error between the end effector and the target

4.2 静态及动态避障实验

本节在第4.1节的基础上添加动静态障碍物来验证机械臂的避障性能,障碍物由一系列点组成,经过快速凸包算法处理转化为凸体.

参数初始化:Kr=10,d0=0.05 m,目标位姿对应的pgoal1,pgoal2如表2中的第1组所示,障碍物的顶点坐标与表3障碍物1一致.其它参数与第4.1节一致.初始化实验配置如图7所示.动态避障时,障碍物速度vobs=[vx,vy,vz],其 中vx=0.0005 m/步,vy=0.0005 m/步,vz=0.0005 m/步.

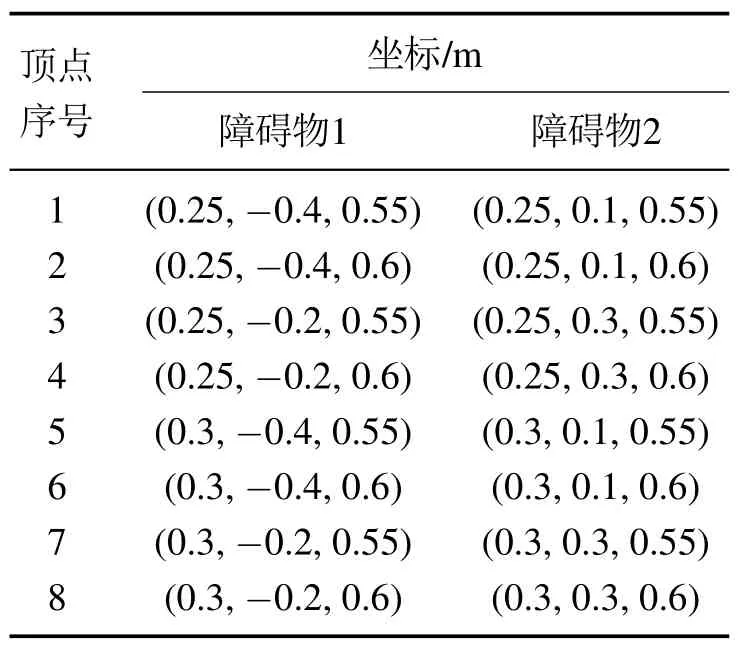
表3 各个障碍物顶点的位置Table 3 The position of the vertex of each obstacle

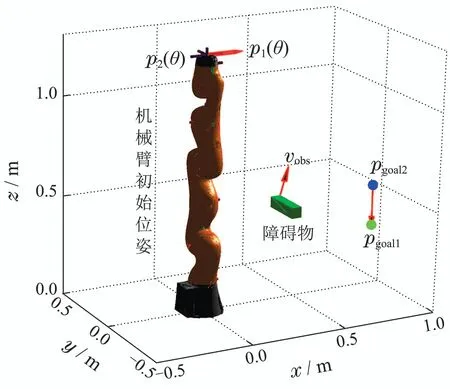
图7 避障实验初始化环境配置Fig.7 Initialization environment configuration of obstacle avoidance experiment

图8为文献[13–16]所提方法(分别为多个球包围盒、椭球包围盒以及球包围盒)与GJK算法对于障碍物的处理以及最近距离的计算,其中p1为机械臂连杆等效面上的一点,p2为机械臂与障碍物之间的最近距离点.从图中可以看出文献[13–16]所提方法会在较大程度上增大障碍物的体积,计算出的最近点在包围盒上,最近距离比实际的要小,而GJK算法计算出的最近点在障碍物凸点上或者在凸点连线上,计算的距离更准确.

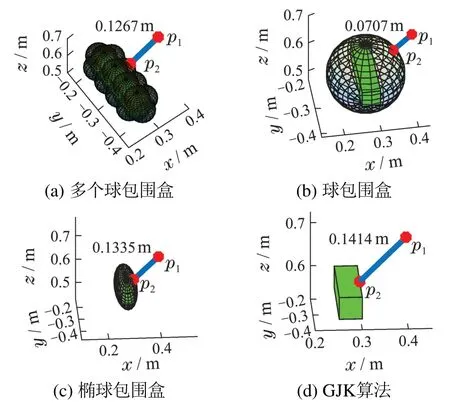
图8 机械臂各连杆等效圆柱面Fig.8 The equivalent cylinders of links of the robot

图9与图10展示了机械臂在到达目标位姿的过程中,各连杆与静动态障碍物之间没有发生接触,说明避障算法是有效的.从图10(a)可以看出各连杆与障碍物之间距离在500步后呈现线性增长,这是因为500步之后,末端执行器比较接近目标,此时机械臂整体的运动就非常慢,而障碍物是匀速运动的,逐渐远离机械臂,因此与机械臂各连杆之间的距离会呈现线性增长;从图10(b)可以看出末端执行器与目标之间的位置误差并不总是逐渐减小的,当动态障碍物距离机械臂很近时,斥力远大于引力,此时机械臂会以避障任务为主,在不与障碍物碰撞的情况下,逐渐接近目标.

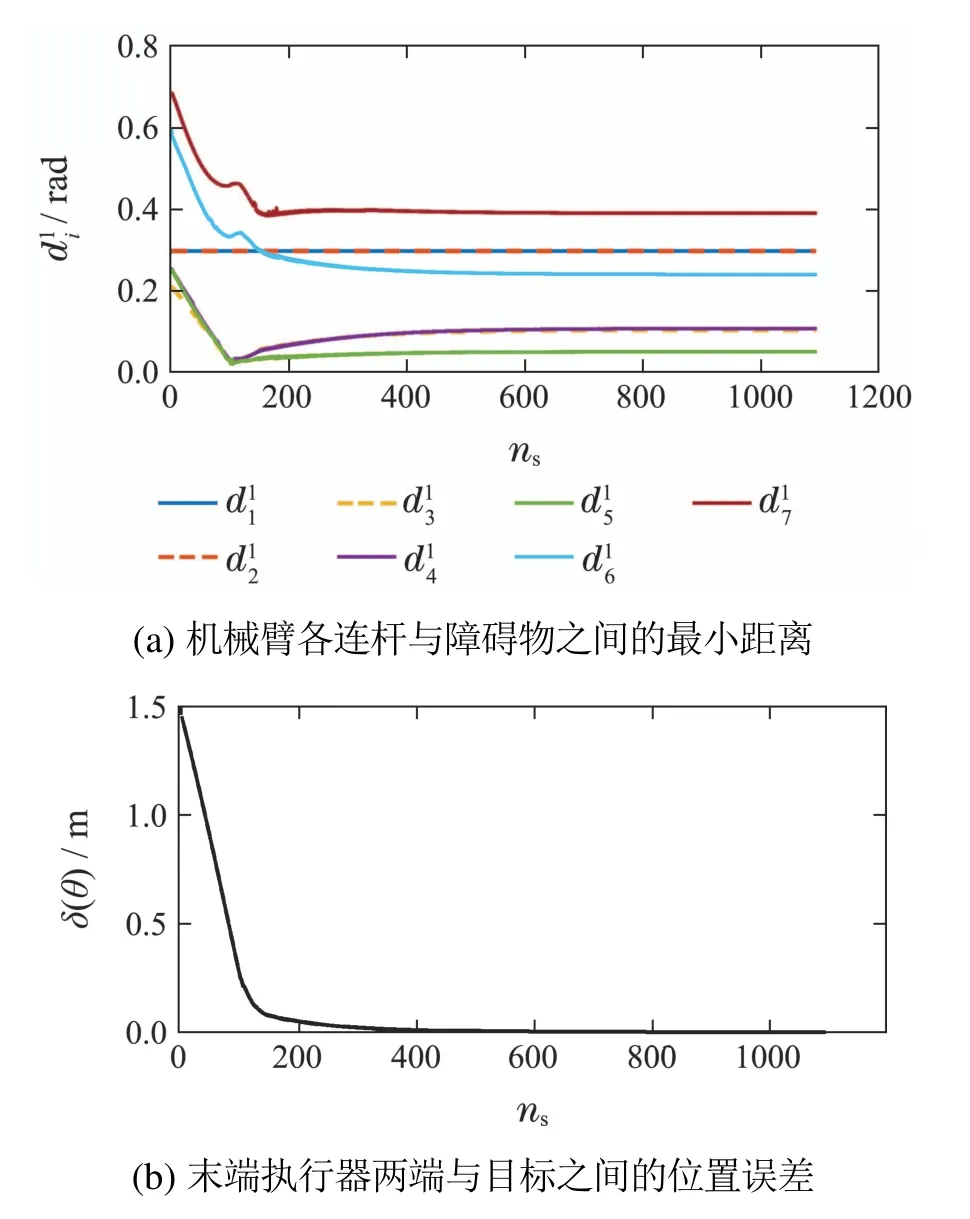
图9 静态避障下机械臂的运动情况Fig.9 The motion of the manipulator in static obstacle avoidance

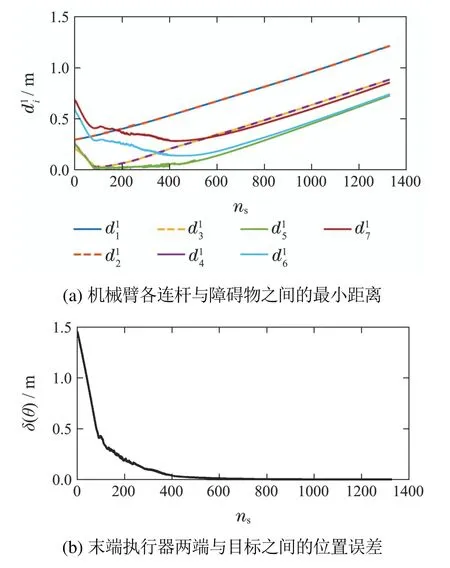
图10 动态避障下机械臂的运动情况Fig.10 The motion of the manipulator in dynamic obstacle avoidance

4.3 局部极小值实验

本节在手术场景中添加多个障碍物,使末端执行器在进行位姿对准的过程中陷入局部极小值,观察机械臂后续的运动状况,进而验证动态引力常数具有逃离局部极小值的能力.

实验场景的初始化配置如图11所示,包括LBR iiwa 7七自由度冗余机械臂(与末端执行器结合)、障碍物、脊柱模型以及带有光学标记物的穿刺针模型,模型大小与实物一致,通过点面信息展示在机械臂坐标系下.

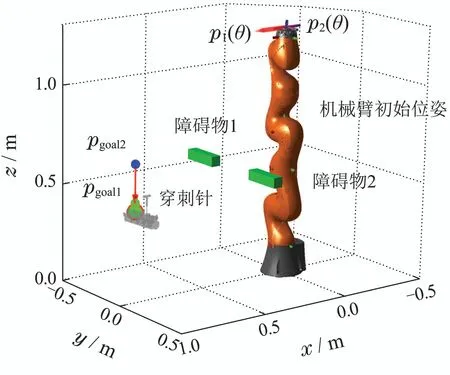
图11 椎弓根螺钉位姿对准实验场景配置Fig.11 Experimental scene configuration of pedicle screw pose alignment

参数初始化:不改变引力常数时,Ka=106:改变引力常数时,Ka=106+r−c.Kr=1,d0=0.05 m,b=6,M=50,δthreshold=10−6m,tcount=400,目 标位姿对应的pgoal1,pgoal2如表2中的第1组所示,障碍物的顶点坐标如表3所示,其它参数与第4.1节一致.

实验中,如果末端执行器在3500步以内未达到目标位姿,则认为机器人到达目标位姿失败.从图12(a)中可以看出,末端执行器与目标位姿之间的距离在302步陷入局部最小值,并在0.06 m附近振荡,无法达到目标位姿.图12(b)为采用动态引力常数后末端执行器与目标之间的距离,其中红点为检测到的局部极小值点,每次出现局部极小值或发生预碰撞后,都会改变引力常数,可以看出,在第4次改变引力常数后,末端执行器达到目标位姿.图13为改进引力常数后,机械臂各连杆与各个障碍物之间的距离,可以看出改变引力常数并没有导致机械臂与障碍物发生碰撞.由此,证明了动态引力常数使机械臂具有逃离局部极小值的能力.

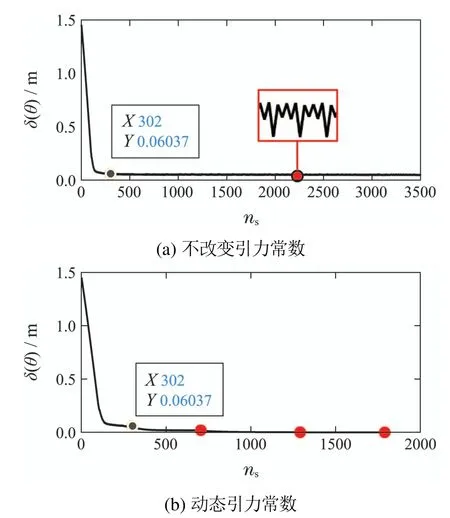
图12 末端执行器两端与目标之间的位置误差Fig.12 Position error between the end effector and the target

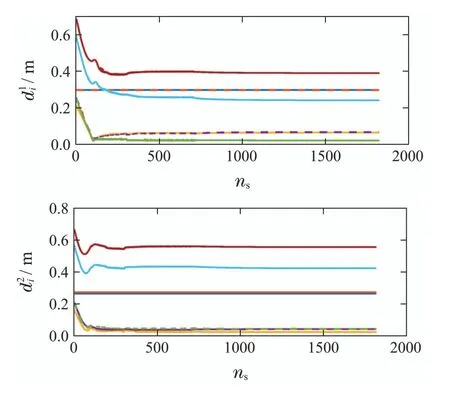
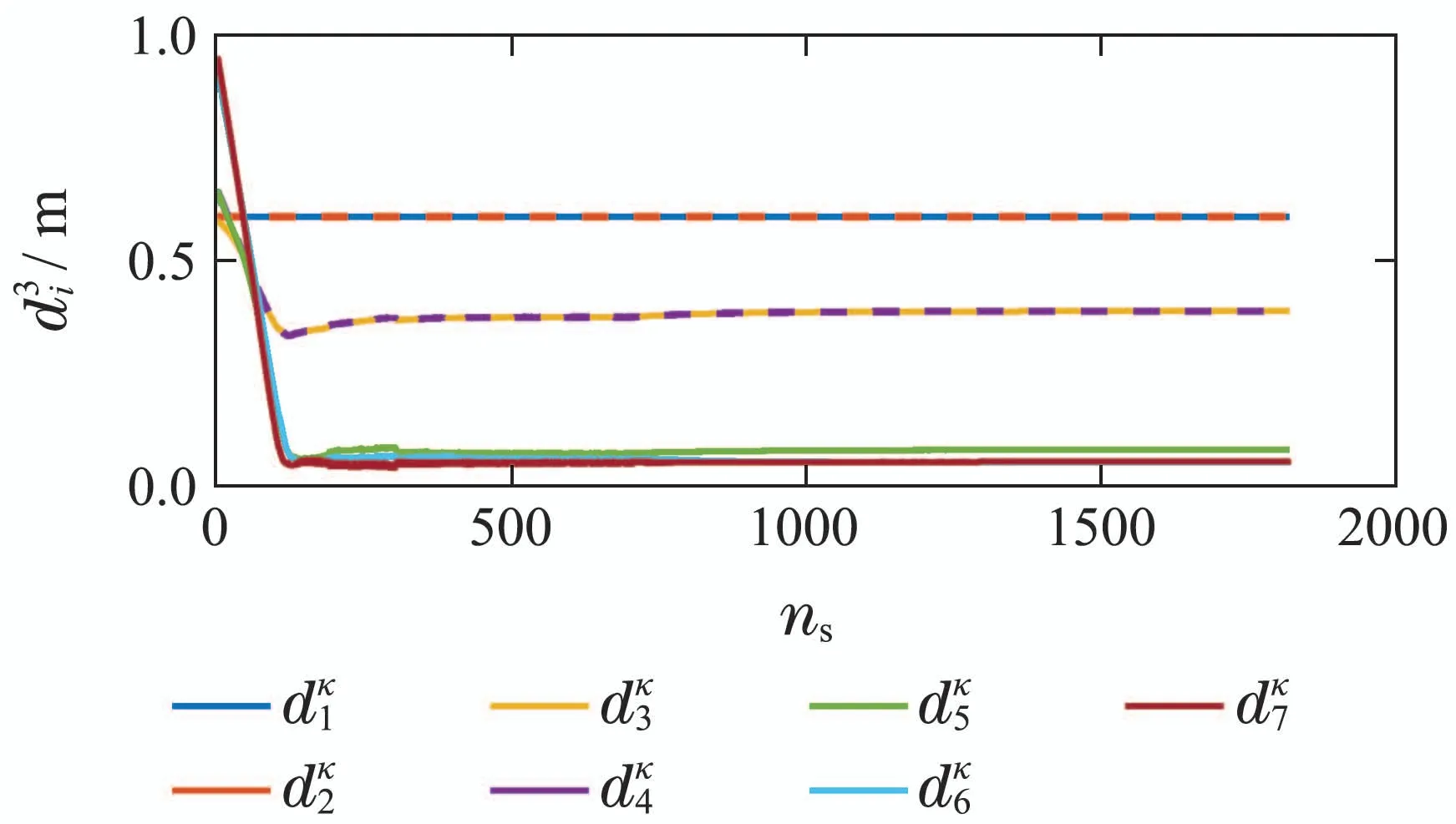
图13 机械臂连杆与各障碍物之间的最近距离Fig.13 The shortest distance between links of the robot arm and the obstacles

5 结论

本研究针对手术机器人自动化手术路径执行中的安全性及准确性问题,提出一种改进人工势场的手术机器人位姿规划算法.在位姿可达方面,对引力函数进行改进,利用两点法约束末端执行器姿态,在无需求取运动学逆解的情况下,准确驱动机械臂到达指定位姿;在避障方面,利用快速凸包算法将障碍物凸体化,通过GJK算法计算障碍物与机械臂连杆等效圆柱面之间的最近距离,使避障距离更加准确;在机械臂运动过程中,通过自适应步长,使其运动更加平稳快速;在陷入局部极小值时,通过动态引力常数,机械臂能顺利逃离.

本研究给定了实验中障碍物点云位置信息,后续会配合视觉系统,捕获真实场景下障碍物的点云,使研究更加符合临床应用.