考虑频域分解后数据特征的空调负荷预测模型

于军琪,边 策,赵安军,解云飞,惠蕾蕾

(西安建筑科技大学建筑设备科学与工程学院,陕西西安 710055)

1 引言

在建筑能耗各大主要的源头中,空调系统能耗占比超过了40%,是重要的能耗系统之一[1].提高能源利用率和节约资源尤为重要,而空调具有巨大的节能潜力[2].Richalet和Cutler[3]提出的模型预测控制(model predictive control,MPC)被视为一种解决空调系统高能耗问题的有效方法.MPC算法本质特征包括预测模型、滚动优化和反馈校正[4].由模型失配、扰动等造成的的不确定性可以通过不断滚动的局部优化及时得到补偿,从而得到较好的动态控制性能.基于负荷预测的MPC策略使系统可以实时追踪空调运行的动态特性,并根据需求实时调节设备参数,实现供需匹配,在保证人员舒适度的前提下,降低系统能耗[5].其中,负荷预测模型的精度是实现HVAC系统非线性MPC策略的重要基础和关键所在[6].

空调负荷预测模型主要分为物理模型和数据驱动模型.物理建模方法计算量大,求解复杂.近年来,涌现出一大批机器学习和人工智能方法结合的研究.对空调逐时负荷预测常采用的方法大致分为人工神经网络(ANN)[7]、时间序列[8]、回归分析[9]以及支持向量机(SVM)[10]等.

ANN通过训练一定数量神经元,可以对冷负荷与输入特征变量之间的复杂非线性关系进行拟合[7].近年来,基于深度神经网络(DNN)方法的预测效果显著,其处理大量样本、高维数据的能力较强,也在短期负荷预测领域中逐渐展开了研究[11].有学者通过选取强相关性的特征作为模型的输入,可以有效提升DNN模型的预测精度[12].隐层数的增加可以降低误差,但会导致模型训练时间过长,甚至会出现“过拟合”情况[13].上述文献并未考虑负荷序列的分解特性,且模型对于数据的依赖性太强,难以解决小样本容量的建筑冷负荷预测的问题.

时间序列预测的基本准则是用事物本身过去的变化特征描述预测未来的变化特征,其计算速度快,能反映负荷近期的连续变化,但对原始时间序列的平稳性要求高[14],而实际空调负荷一般不满足严格平稳性的要求,而回归法在解决非线性问题有一定的缺陷,因此预测效果不理想.

SVM[15]是由Vapnik等人提出的一种专门研究小样本情况下机器学习规律的理论,解决了ANN等智能算法需要大量训练样本的问题.而Suykens在SVM的目标函数中引入误差平方和项,并提出最小二乘支持向量机(least-square support vector machines,LSSVM)方法,该方法收敛精度高[16],解决了样本训练过程中计算速度慢的问题,且具有较好的非线性拟合能力,被许多学者成功应用于负荷预测中[17].极端梯度提升树(eXtreme-gradient boosting,XGBoost)模型是一种特殊的梯度提升决策树,是基于树结构并结合集成学习的一种方法,在分类回归树(CART)的基础上引入了集成学习方法,以出色的鲁棒性和高效的运算速度在负荷预测领域得到广泛应用[18].

建模应当根据数据本身的特点来构造合适的预测模型.空调负荷数据具有非线性、非平稳特性,且随着人流波动、天气等因素的影响体现出一定的随机性.而单一预测模型未能充分考虑负荷序列中隐含的重要信息,很难反映原始信号的变化机制.为了进一步挖掘冷负荷序列的局部细节特征,各种信号分析分解方法被广泛地运用在预测中,用以挖掘时间序列所蕴含的更深层次信息,如小波变换法[19]、经验模态分解法(EMD)[20]、局域均值分解法[21]等.Dragomiretskiy[22]提出了变分模态分解(variational mode decomposition,VMD)的信号处理方法,实现固有模态分量(intrinsic mode functions,IMF)的有效分离、信号的频域划分,表现出更好的噪声鲁棒性[23].

本文在已有研究基础上,利用VMD算法对负荷序列从频域的角度挖掘、提取负荷的局部细节特征,通过随机森林(random forest,RF)剔除输入变量之间的冗余信息,分别采用LSSVM、XGBoost模型建立负荷的非线性、线性子序列预测模型,对噪声部分的概率分布进行拟合,最后重构叠加各子序列预测结果得到最终负荷预测结果,仿真实验结果表明了所提出方法的有效性和可行性.

2 预测模型的建立

2.1 VMD算法

VMD采用完全非递归的方式求变分模型的最优解,根据各分解分量的中心频率和带宽,自适应地将原始信号分解为具有特定稀疏性的有限带宽的模态集合.其模态的带宽是通过希尔伯特变换获得单侧频谱,然后通过混合中心频率将模态频谱调制到相应的基频带信号,并计算解析信号的梯度平方L2范数而得到的,因此,分解过程是通过解决一个约束变分问题来实现的,如式(1)所示:

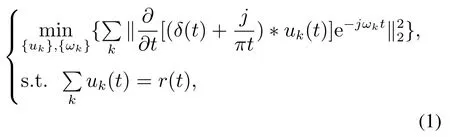
式中:{uk}={u1,u2,···,uK}为模态分量集合;{ωk}={ω1,ω2,···,ωK}为模态中心频率集合;δ(t)为单位脉冲函数;r(t)为输入负荷序列.

引入二次惩罚因子α和拉格朗日乘子λ,将式(1)转换为无约束变分问题,如式(2)所示:

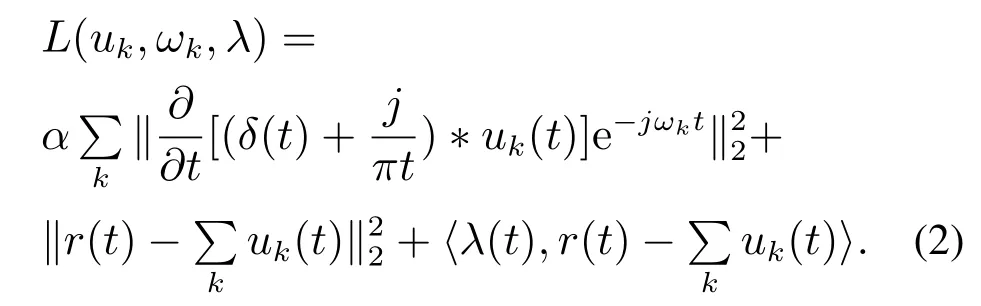
用乘子交替方向法迭代更新uk,ωk及λ,得到各模态分量最优解

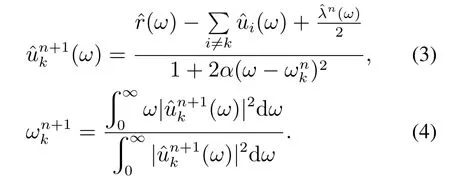
直到满足约束条件(5),输出最终模态分量.

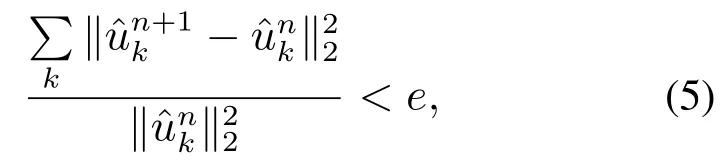
式中e>0为判别精度.

2.2 LSSVM模型

LSSVM用等式代替不等式约束,并将线性最小二乘准则应用于损失函数优化,实现了凸二次规划问题向线性方程组问题的求解转变,提高了收敛速度.其实现过程如下:

1) 训练数据集{(x1,y1),(x2,y2),···,(xn,yn)}中xi是第i个输入样本,yi是输出变量,采用核函数映射在高维空间中构造回归函数

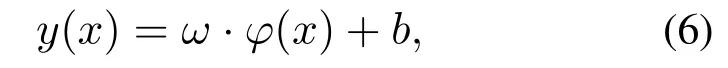
式中:ω为为权向量,φ(x)是非线性核映射函数,b为偏差参数,“·”表示内积.

2) 根据结构风险最小准则,最优ω和b可经下述函数最小化得到

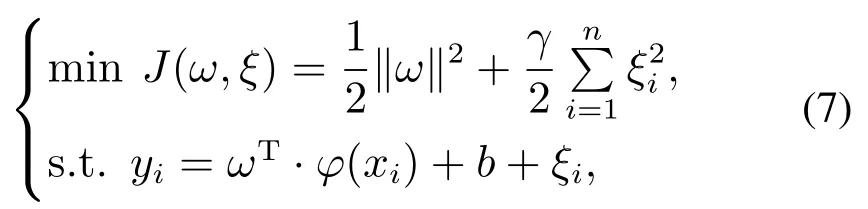
式中:γ为正则化参数,ξi为松弛变量.

3) 构造如下拉格朗日函数:

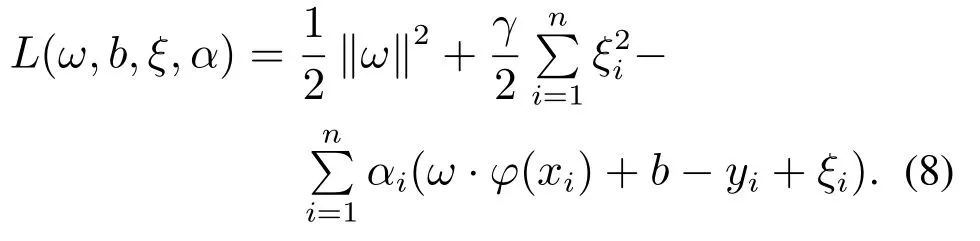
此处αi是对应于xi的Lagrange乘子.

4) 根据KKT(Karush–Kuhn–Tucker)条件,分别求解L(ω,b,ξ,α)对(ω,b,ξ,α)的偏微分,并消去xi和ω之后,可得到如下矩阵表达形式:

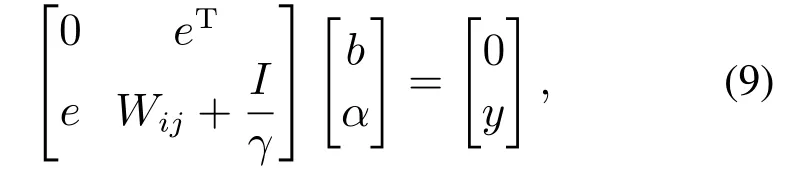
其中:e=[1 1···1]T,α=[α1α2··· αn]T,I为单位矩阵,Wij=φ(xi)·φ(xj)=k(xi,xj),k(xi,xj)是核函数矩阵.

5) 求解优化问题后LSSVM模型的输出为

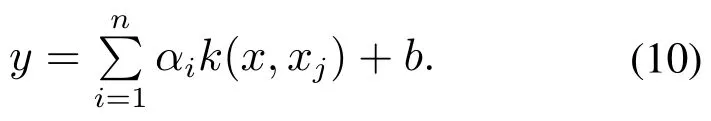
2.3 XGBoost模型

XGBoost模型是对GBDT模型的改进,由多棵决策树迭代组成.其回归算法主要步骤如下:

1) 构造目标函数.

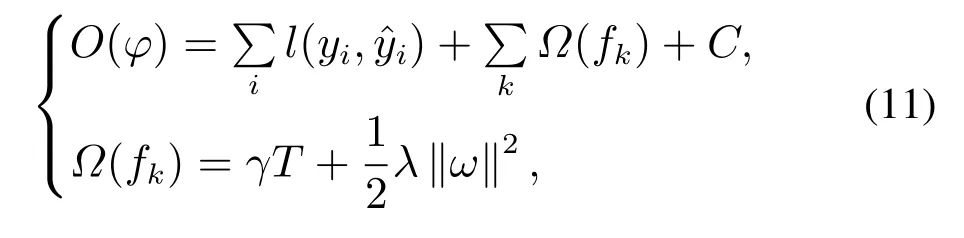
式中:yi与分别为真实值与预测值;K为学习器个数;T为叶子节点个数;ω为叶节点的数值;C为常数;l为误差函数;Ω(fk)为正则化项;γ与λ为控制参数,用来防止过拟合.

2) 基于GB思想,第t轮的学习器等于前t −1轮的学习器加上ft,逐步优化每一棵树,获得代价最小CART树

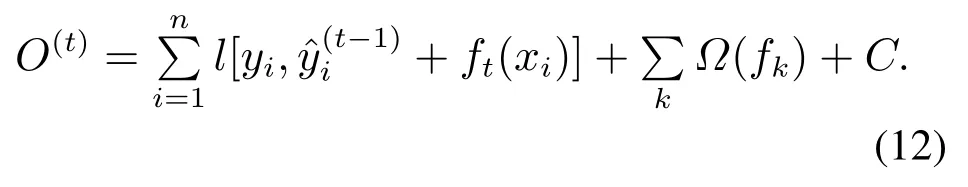
3) 在构建第t个学习器时要寻找最佳的ft,来最小化目标函数.利用ft=0处的泰勒二阶展开并去除常数项将目标函数近似为

4) 令集合Ij={i|q(xi)=j}为叶子j的集合,化简式(13)得

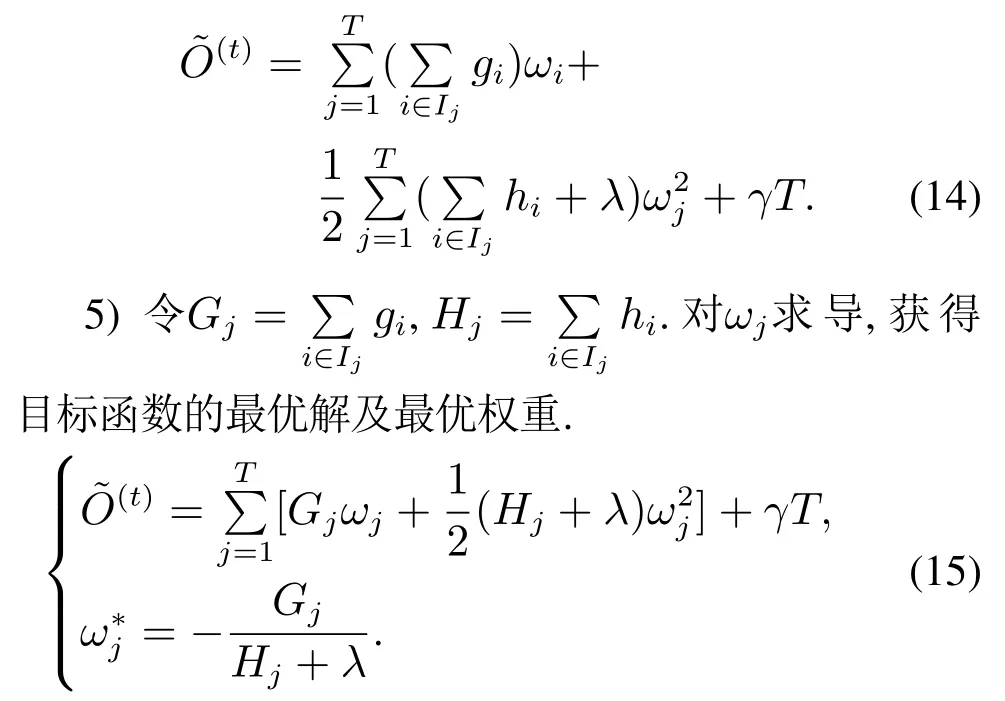
2.4 本文思路

本文所提出的VMD-LSSVM-XGBoost-ERR模型具体实现过程如下:

步骤1特征选择(feature selection,FS).通过RF筛选出特征重要度较高的因素.

步骤2信息提取.利用VMD将冷负荷序列分解成离散的具有不同的中心频率的子序列IMF1,IMF2,···,IMFn.在确保数据分解的保真度前提下减弱原始序列的非平稳特性,以提高预测的精度.

步骤3模型的训练和验证.采用第一步所得因素作为LSSVM、XGBoost模型输入,分别对IMF1和IMF2序列进行预测,采用正态分布模型对IMF3序列进行预测.各个子序列的预测结果进行线性叠加即为冷负荷的最终预测结果.

步骤4模型评价.采用MAPE,RMSPE和R2评估所提出的模型的性能.

3 仿真实验与结果分析

本文以西安某大型公共建筑6月,7月每天早八点至晚十点实际采集的数据为例进行分析.该建筑物总面积30万m2,商业面积28万m2,其中建筑空调采暖面积28万m2.数据采样间隔为1 h,样本容量为700组,其中80%作为训练集,20%作为测试集.所提算法均使用Python3.3实现,实验均在内存为8 GB、处理器为Intel Corei5-6200U CPU 2.30 GHz的计算机中进行.

3.1 实验数据分析与处理

3.1.1 数据降维

通常以T时刻的数据作为冷负荷预测模型的输入,考虑到冷负荷的时间序列性,还将(T −1)h以及(T −2)h时刻冷负荷作为模型输入变量.

表1为各特征变量重要度排序.从表1可以看出,设定重要度阈值为0.1,最终选择(T −1)h冷负荷、太阳辐射、(T −1)h太阳辐射、(T −2)h冷负荷、室外干球温度和相对湿度作为模型输入.

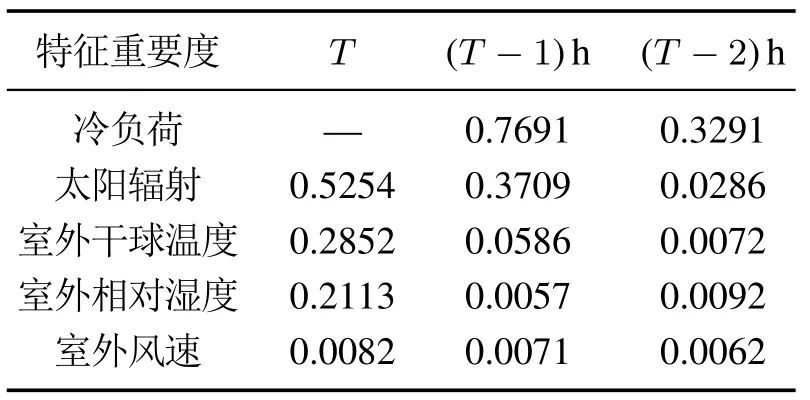
表1 影响负荷特征变量重要度Table 1 Importance of variables affecting coolingload

3.1.2 VMD负荷序列分解

参数设置:惩罚参数α=1500,初始中心频率ω=0,收敛判据r=10−8.模态数量K通过各模态的中心频率是否出现相近模态来确定.模态函数个数经过多次实验得出表2,可以看出在模态分量个数K=4时,中心频率922 Hz和1186 Hz相距较近,K=5时,中心频率896 Hz和1075 Hz相距较近,均可能出现模态混叠.为了保证实际信号分解的保真度,模态个数选为3较适宜.

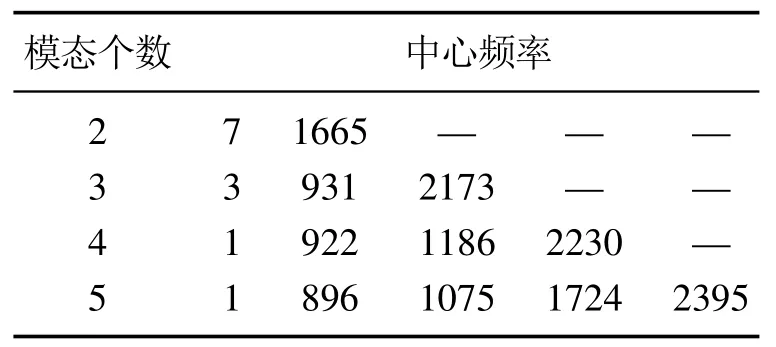
表2 不同K值对应的中心频率Table 2 Center frequency corresponding to different K

当K=3时,采用VMD分解的结果如图1所示,可以看出每条分量反映出不同的信息.

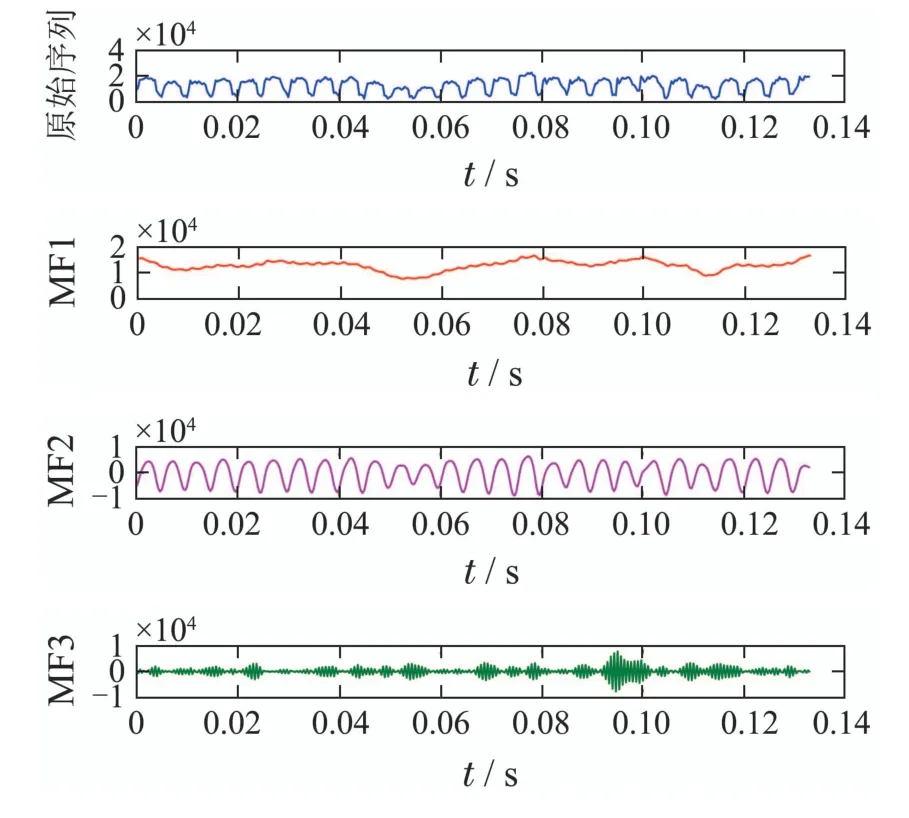
图1 VMD分解结果Fig.1 VMD decomposition results

从图1中可以看出,IMF1反映出冷负荷的大体变化趋势,具有明显的非线性特性.IMF2具有波动特性,且周期性明显.ERR序列随机分布在0附近,其规律性较差.对各序列分别进行ADF检验[24].设原假设H0:存在单位根,即该序列为非平稳序列;备择假设H1:不存在单位根.检验结果如表3所示.

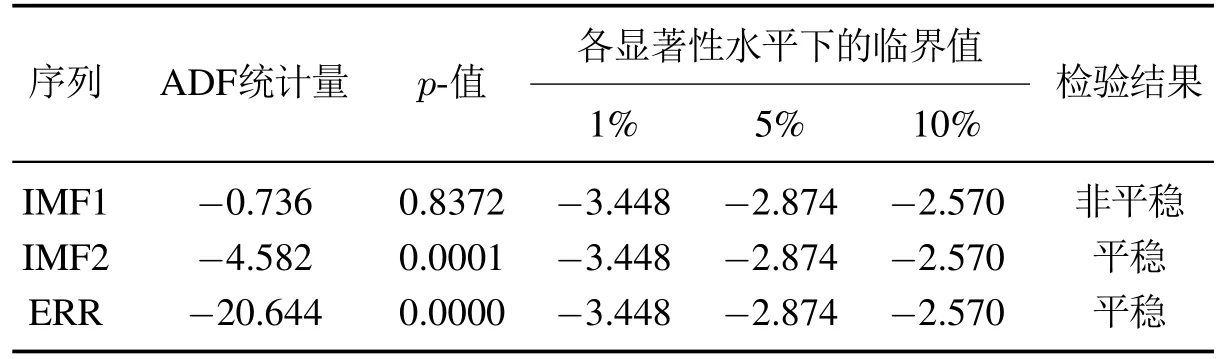
表3 ADF检验结果Table 3 ADF test results

由表3可知,IMF1序列的ADF统计量为−0.736,该值明显高于各显著性水平下的临界值,且p-值大于各显著性水平,因此,接受原假设,认为该序列为非平稳序列;IMF2 和ERR 序列的ADF 统计量分别为−4.582和−20.644,均小于各显著性水平下的临界值,证明两者不存在单位根,属于平稳序列.ERR序列散点在0附近随机波动,没有明显的趋势,因此可以看作是噪声部分.该序列的频率直方图及拟合概率分布如图2所示.则设定正态分布为待检验的分布类型,对ERR作出相应的正态Q-Q图及去趋势正态Q-Q图,如图3所示.

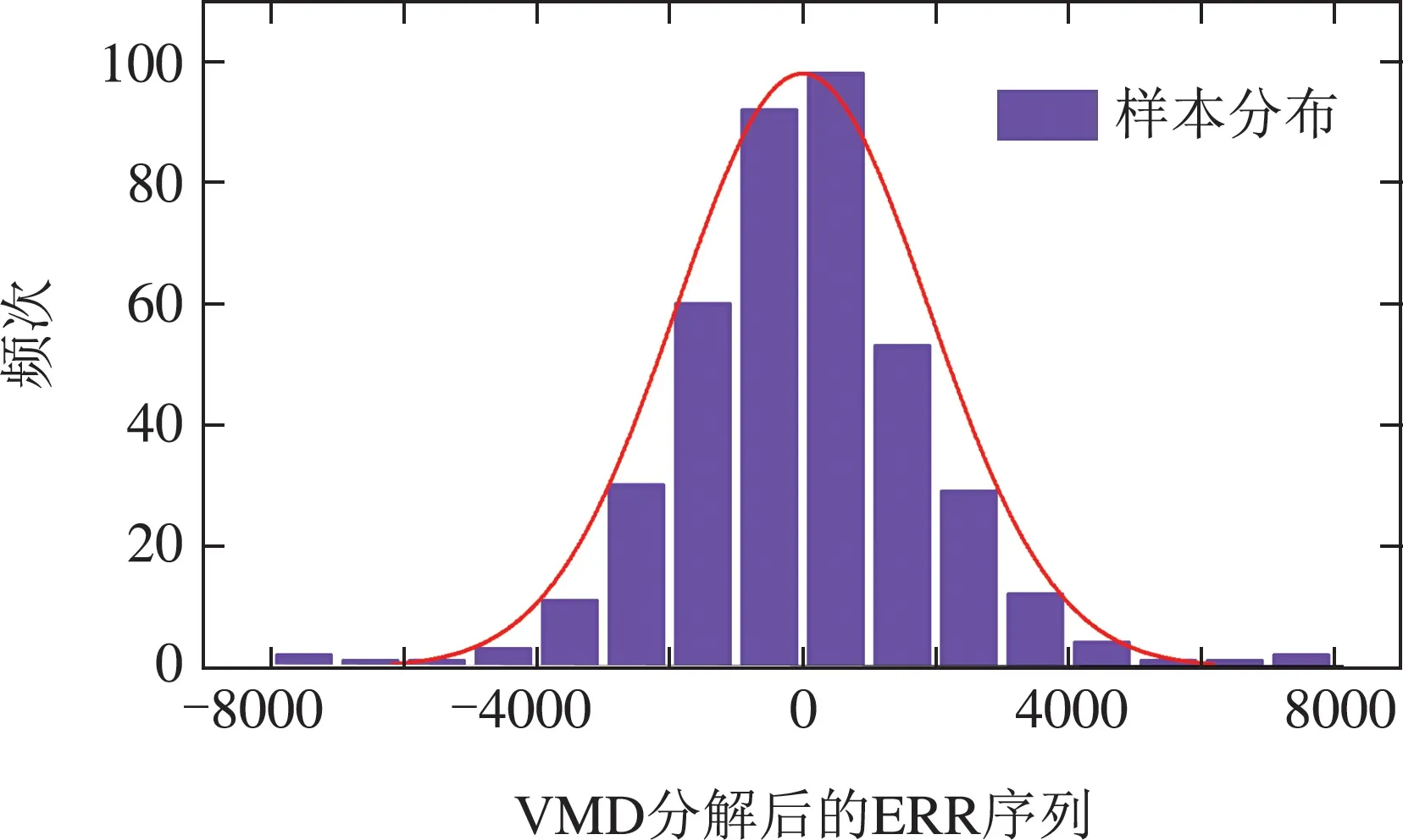
图2 ERR序列的频率直方图及拟合概率分布图Fig.2 Frequency histogram and fitting probability distribution of ERR sequence

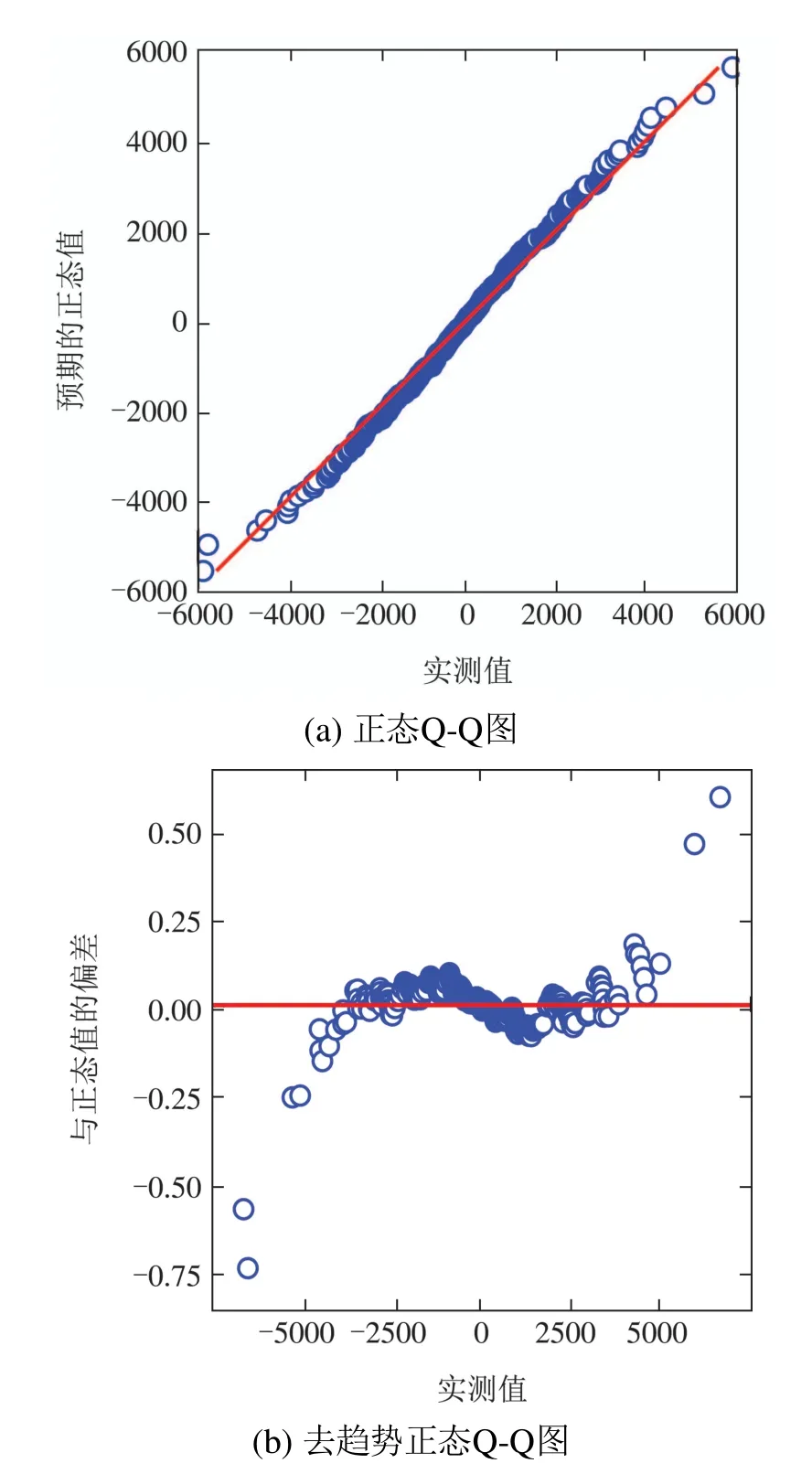
图3 ERR序列正态检验结果Fig.3 Normal test results of ERR sequence

在图3(a)中,绝大部分的样本点基本呈直线分布,这表明被检验的样本分布与已知分布基本一致,并且散点分布在斜率为1892.311,截距为0.001的直线附近.

残差情况如图3(b)所示.可以看出,残差散布基本上是随机的,在0值上下波动,具有均匀性和对称性.Q-Q图主要偏差范围在区间[−0.25,0.25]内,偏差变化值小,并且在置信范围内.用Kolmogorov–Smirnow进行一元正态性检验[25],结果为p值大于0.05.通过上述分析可知ERR 序列服从均值为0.001,标准差为1892.311的正态分布.

3.2 预测结果

3.2.1 IMF1子序列预测结果

首先对IMF1子序列采用LSSVM,XGBoost,LSTM和CNN 4种模型分别进行预测,各预测模型的超参数设置如下:

LSSVM:核函数为rbf,其系数为1500,γ为300;

XGBoost:选择提升器为gbtree,树深度为5,学习率为0.09,最小叶子节点样本权重为4,随机采样比例为0.08,迭代次数为1000;

LSTM:神经元数量为40,20,隐藏层为2,学习率为0.05,输入步长为8,输出步长为6;

CNN:卷积核数依次为32,64,128和256,核大小为1,操作步长为1,输入量延迟为0.01 s,激活函数Relu.

图4为4种模型的预测误差分布统计图,可以直观的看到,XGBoost和CNN在高误差区分布较多,分布数据的标准差较大.而LSSVM模型相比于LSTM模型,误差分布更加集中在小误差区,对IMF1的预测结果最精确.

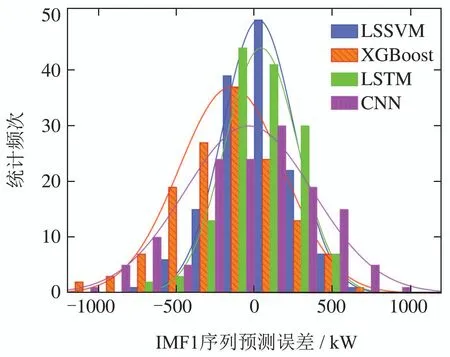
图4 不同模型对IMF1序列的预测误差分布Fig.4 Distribution of prediction error of IMF1 by different models

表4展示了各模型对IMF1子序列训练数据和测试数据的拟合精度以及模型运行耗时.由表4可得,LSSVM模型的MAPE指标和CVRMSE指标均低于XGBoost,LSTM和CNN模型,分别为1.341%,0.0170,且R2为0.9582,均高于其他3种模型.其中,LSTM模型的运行时间较长,而XGBoost模型的运行时间最短,但其预测误差较大.综合来看,LSSVM模型的预测效果更好.

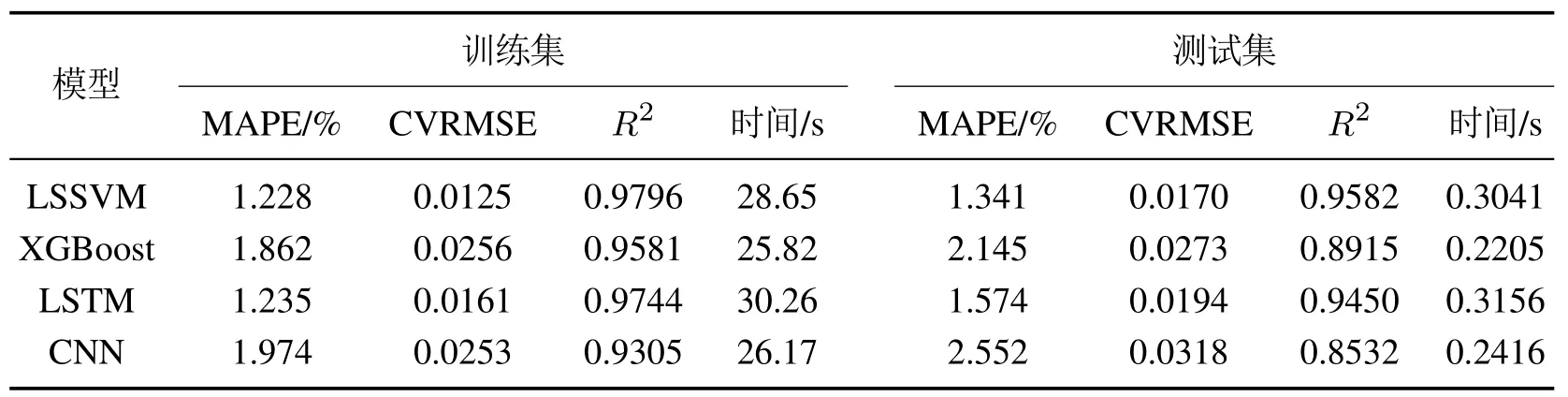
表4 各模型对IMF1子序列预测精度及效率比较结果Table 4 Comparison results of prediction accuracy and efficiency of each model for IMF1

3.2.2 IMF2子序列预测结果

同理,采用上述模型对IMF2子序列的预测结果分别如图5和表5所示.由图5可以看出,XGBoost模型的预测误差分布的标准差较小,基本集中分布在低误差带,表5表明XGBoost模型的各项评价指标均略优于其他3种模型,且在模型时间复杂度上也具有明显优势.因此在本文研究中选择它作为IMF2序列的预测模型.

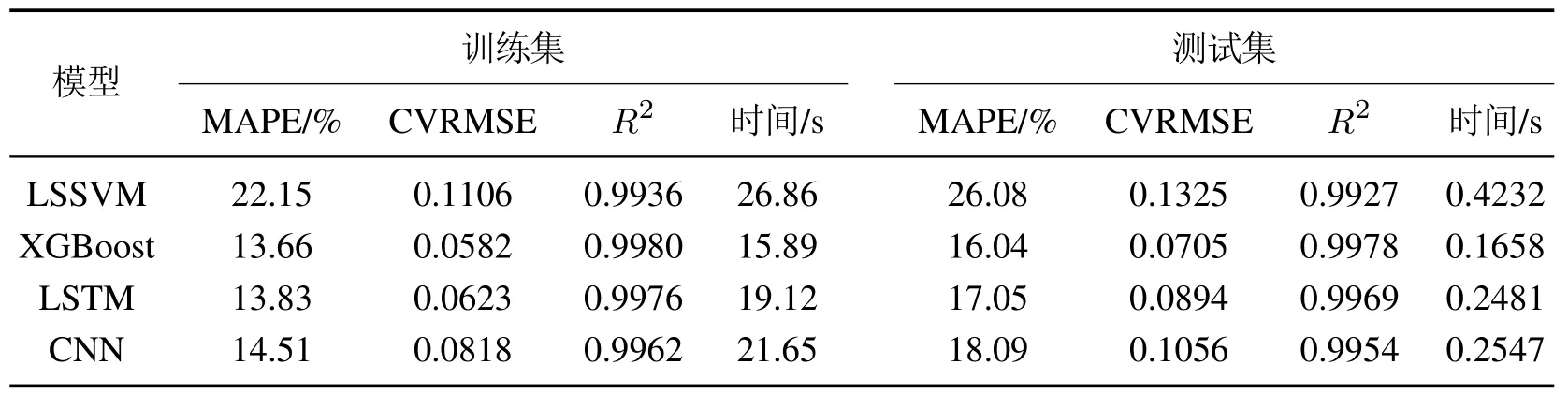
表5 各模型对IMF2子序列预测精度及效率比较结果Table 5 Comparison results of prediction accuracy and efficiency of each model for IMF2

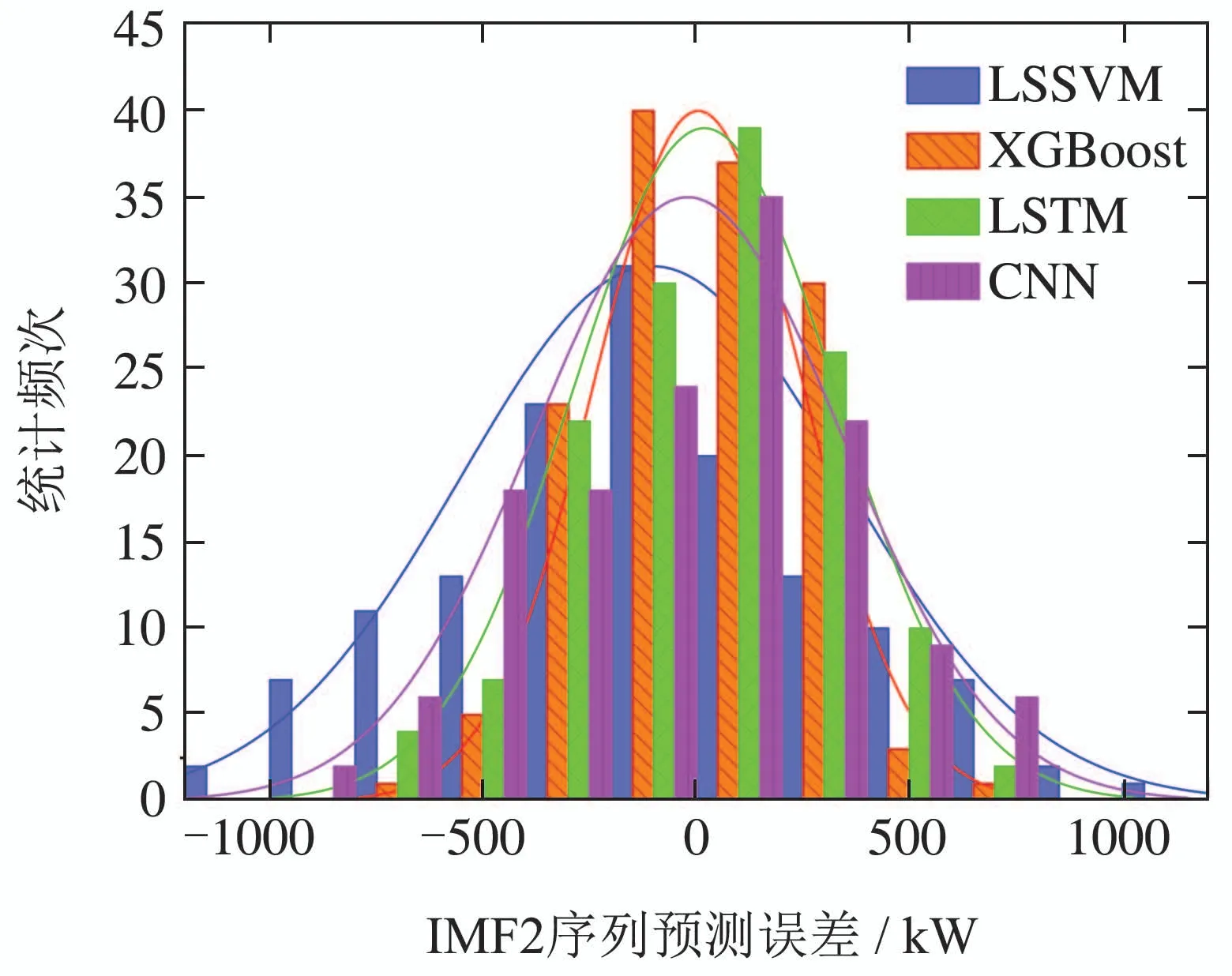
图5 不同模型对IMF2序列的预测误差分布Fig.5 Distribution of prediction error of IMF2 by different models

3.2.3 ERR子序列预测结果

由第3.1.2节分析可知,分解后的ERR子序列服从均值为0.001,标准差为1892.311的正态分布,通过该分布密度得到ERR序列的预测值,将其预测结果与ERR序列真实值进行对比检验,结果如图6所示.

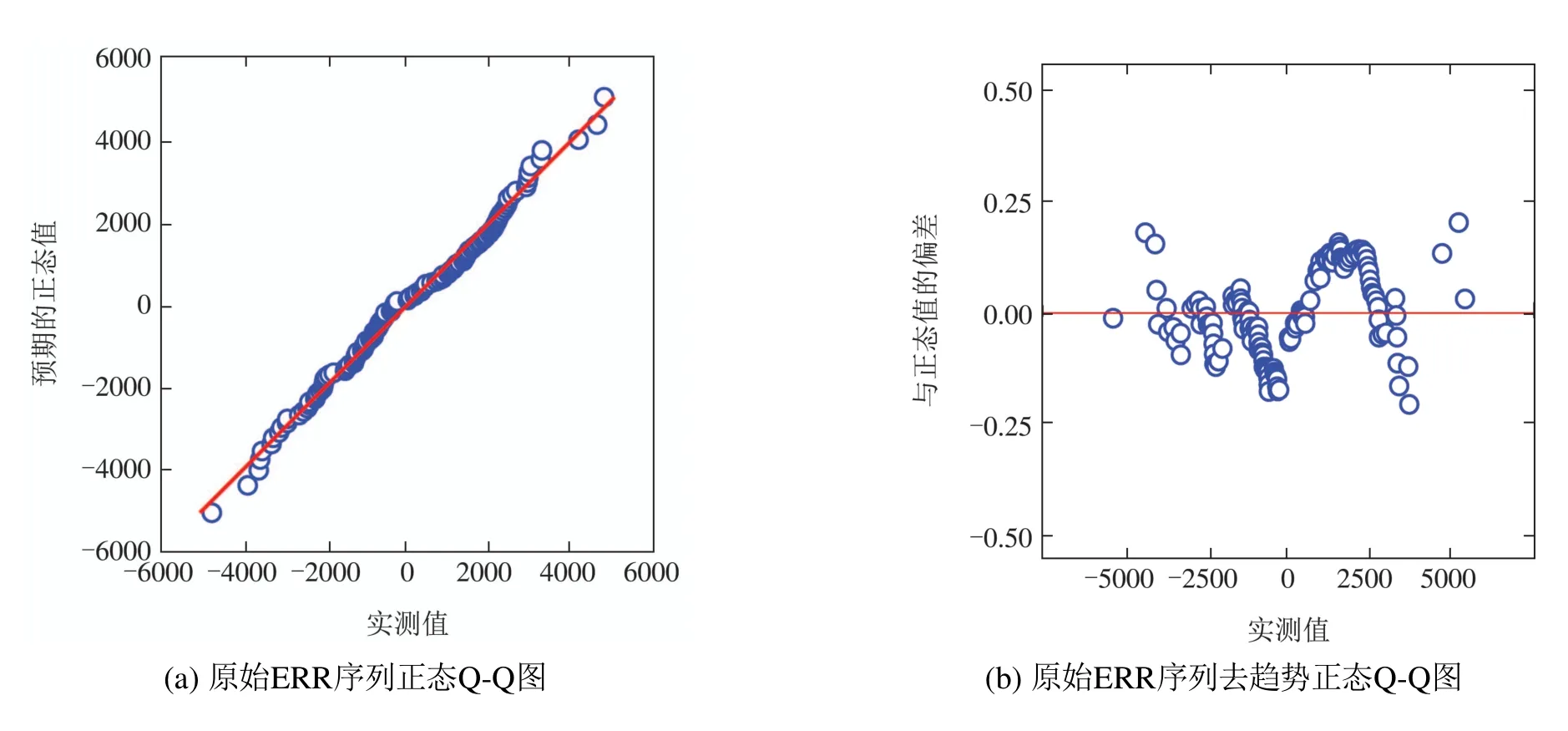
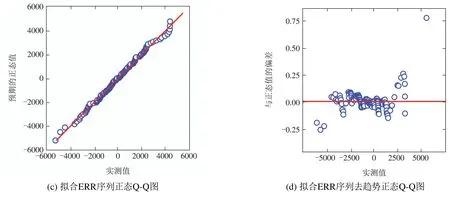
图6 ERR序列的正态分布拟合结果Fig.6 Normal distribution fitting results of the ERR sequence

从图6中可以看出拟合的结果与ERR序列真实值均符合正态分布,且几乎服从同一正态分布,准确体现出该序列的随机误差分布特性.

3.2.4 负荷预测结果

采用LSSVM,XGBoost,LSTM,CNN,VMD–LSSVM,VMD–XGBoost,VMD–LSSVM–XGBoost 和VMD–LSSVM–XGBoost–ERR等8种模型进行建筑冷负荷预测,并分别计算各模型MAPE,CVRMSE,R2.其训练精度和测试精度如表6所示.

分析表6可知,VMD–LSSVM–XGBoost和VMD–LSSVM–XGBoost–ERR这两种复合模型预测结果明显更接近实际负荷.前者的预测结果体现了负荷的总体趋势和非线性特性,但不能完全反映负荷随人流量等因素带来的随机波动特性.后者模型充分考虑了随机性和不确定性,预测效果是几个模型中最好的,还原了实际负荷的动态特征.两者模型的各项误差指标差异很小,这是因为ERR序列服从均值为0的正态分布,因此没有显著提高模型预测精度,也没有影响VMD–LSSVM–XGBoost模型预测的整体趋势.虽然这两者模型的误差指标相似,但后者加入了随机误差序列,反映了负荷的随机波动,通过减小模型误差的离散度和波动范围提高了预测模型稳定性.

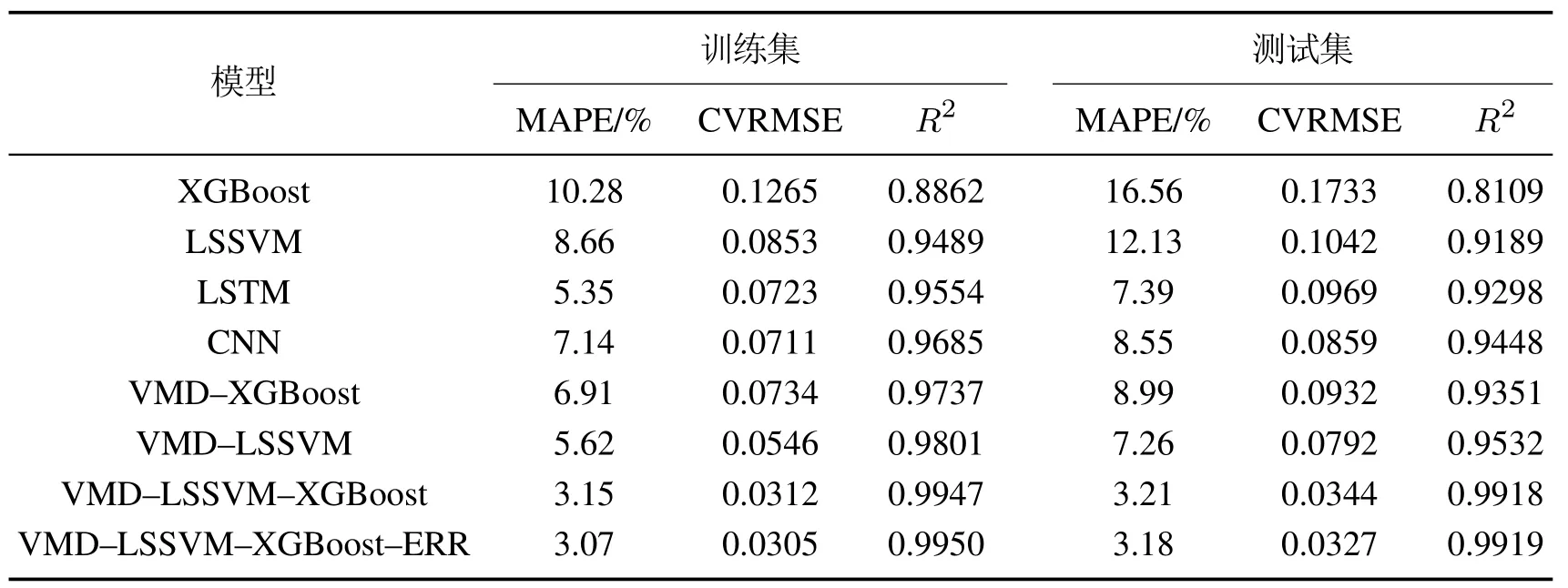
表6 不同模型对冷负荷的预测精度及效率Table 6 Prediction accuracy and efficiency of different models for cooling load

各模型的预测值与实际值逐点相对误差柱状图如图7所示.可以直观地看出,8种模型的相对误差中,VMD–LSSVM–XGBoost–ERR模型的相对误差柱明显最小,从而进一步验证了所提方法的有效性.

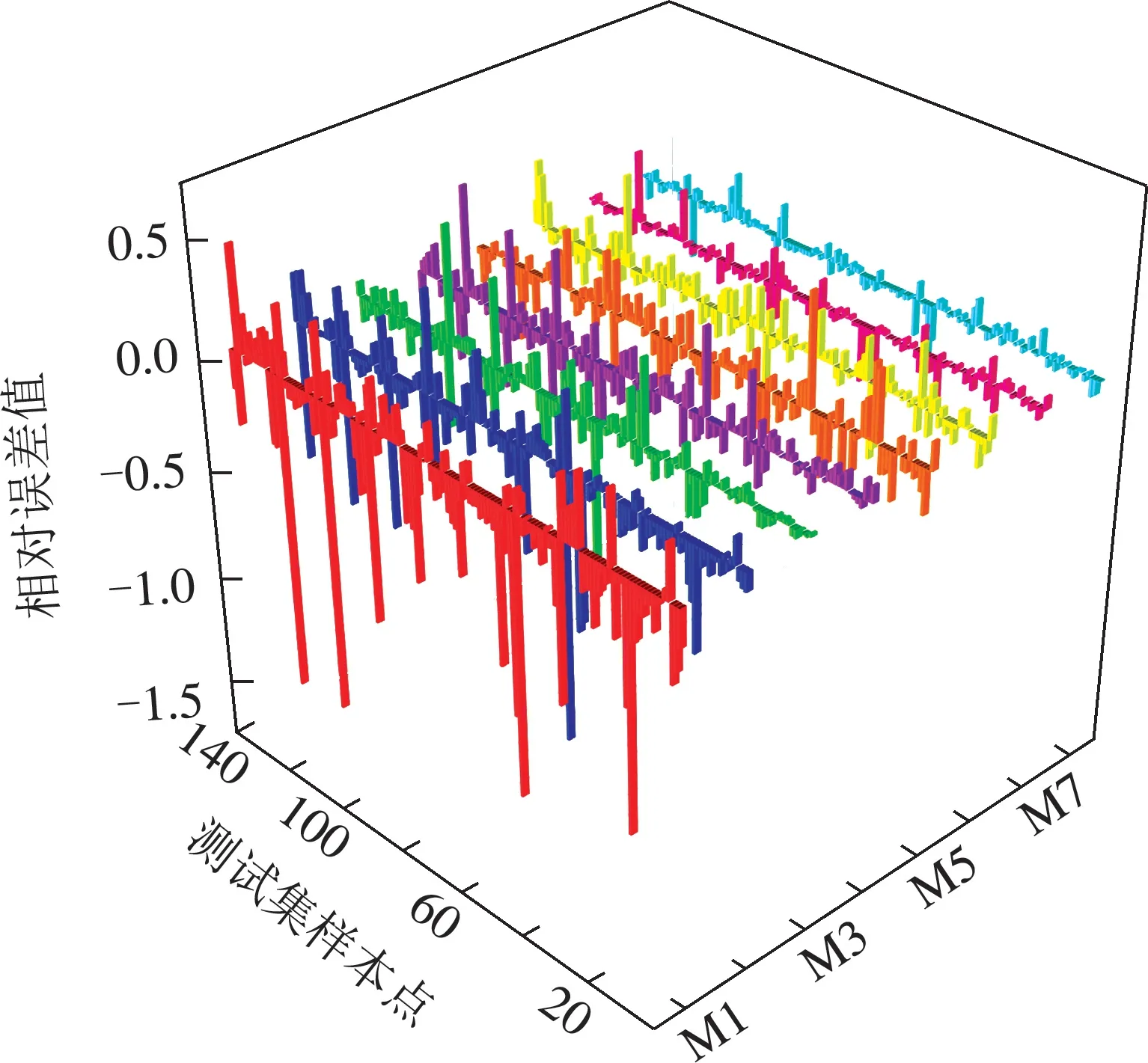
图7 各模型预测值与实际值相对误差柱状图Fig.7 Histogram of relative error between predicted value and actual value of each model

3.3 模型泛化能力验证

用9月4个未参与建模的工作日运行样本进行测试,得到各模型的预测误差,如表7所示.

对比表7可知,单一预测模型的误差基本在10%,性能最差.VMD–LSSVM–XGBoost–ERR模型能够较为准确地反映冷负荷变化趋势,进而验证了本文所提模型在小样本的情况下也可保证良好的拟合精度,同时还有着较强的泛化能力.

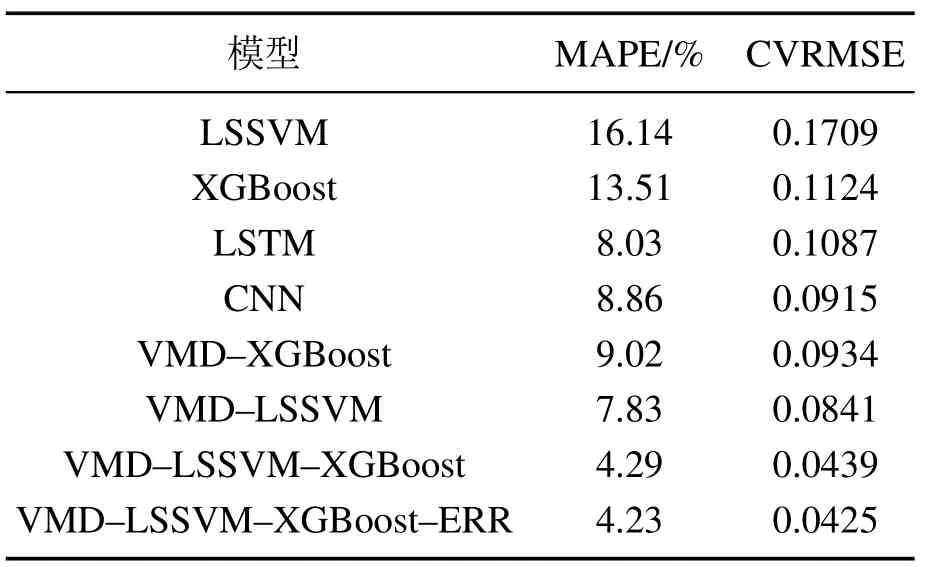
表7 泛化能力的验证Table 7 Verification of generalization ability

3.4 时间复杂度分析

表8为运行8种预测模型特征选择前后所消耗的时间.分析表8可知,通过RF进行特征选择,在维持预测精度的前提下,预测模型的时间复杂度大大降低,但因为在同一实验环境下本文所提出的预测方法在时间上相比于其他七种算法的运行时间略高,因此可以看成本文所提出的预测方法是以牺牲时间复杂度来提高预测精度,但所提升的预测精度远高于所牺牲的时间复杂度代价,且在实际工程应用中,所提出模型的耗时的增量不会引起滞后问题.

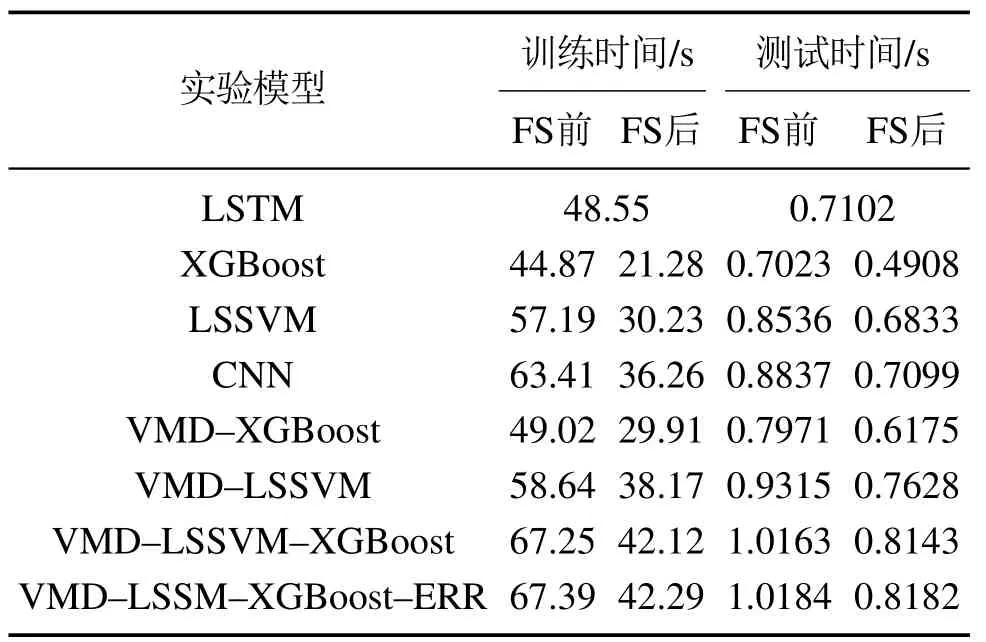
表8 不同模型预测效率对比Table 8 Comparison of efficiency of different models

4 结束语

准确的空调负荷预测是系统节能优化控制策略的关键.本文通过RF算法对采集到的影响因素数据进行特征选择,提高了预测效率,利用VMD算法对大型公共建筑负荷序列进行分解,能够细致把握负荷信号的不同频率中心的变化所表现出来的特征;分别对分解后的趋势序列建立LSSVM预测模型,时序平稳序列建立XGBoost预测模型,采用正态分布拟合随机误差,将这3部分进行重构,建立了VMD–LSSVM–XGBoost–ERR网络的空调负荷预测模型,弥补单一模型对原始信号预测的局限性.通过对比仿真实验结果,证明了该模型在空调负荷预测中的有效性和可靠性,可以准确描述负荷的非线性、波动性以及随机性特征,为空调节能优化运行策略提供较为可靠的数据支撑.