连续型同心管机器人正运动学快速求解方法

冯子俊,李永强,冯 宇,冯远静,刘 扬

(浙江工业大学信息工程学院,浙江杭州 310023)

1 引言

随着科技的发展和医疗水平的进步,可以在一定程度上减少患者身体创伤以及手术开销的微创手术(minimally invasive surgery,MIS)已经逐渐成为了手术领域的一个重要分支[1],而由于部分病灶点所处的位置周围有重要的组织和血管,且手术不允许对患者有任何程度的二次损伤,故在特定的手术中引入精密的机器人是医疗水平向前发展的必然趋势[2].其中同心管机器人(concentric tube robots,CTRs)作为一种特殊的连续体机器人,在微创手术等一些狭小空间中具有很大的市场应用潜力[3].

目前,根据机器人末端有无外力,可将同心管的建模方式分为两类.不考虑负载的建模方式主要分为忽略扭转的刚性模型(torsionally rigid model)[4]以及更精确的柔性扭转模型(torsionally compliant model)[5],也有相关文献在此基础上考虑了管间摩擦力对运动学模型的影响[6–7].文献[8–9]对末端受外力的同心管进行了精确的建模.因为模型的计算复杂度会随着更多力学因素的引入而增加,故需要在模型计算效率和精度上达到一个较好的平衡.

同心管机器人正运动学的计算方法主要包括:根据本构方程(constitutive equations)和静力学平衡建立微分方程求解,或者根据能量最小原则求解[10].但由于能量法是一个计算最优的过程,在参数过多时会出现严重的突变,而微分方程的建模思路更加直接,故本文使用后者进行运动学的计算.在实际应用中,为了使机器人精确稳定地到达目标位置,同心管的设计一般满足分段常曲率(初始状态下,管预弯曲部分曲率恒定)和主宰刚度(两管重合的部分,内管形状服从外管)的要求,以使其在运动过程中能满足其余点跟随末端点的运动方式(follow the leader,FTL)[2,11–12].

目前同心管机器人的正运动学几乎都使用两步积分法[5–9,13],该方法能够达到较可观的精度,但因为这是一种纯数值方法,计算时间较长,不利于机器人的实时运行;为了提高计算速度,文献[14]提出了一种快速柔性扭转机器人模型,通过引入全局变量,建立了欧拉角与曲率的关系式,使计算机能以毫秒级的速度计算出当前的位置信息,但该方法需借助力矩传感器来实时获取扭转力矩.

同心管机器人的正运动学是其逆运动学或实施闭环控制的基础.在逆运动学中需要多次调用正运动学计算过程;在闭环控制中,以模型预测控制(MPC)的同心管闭环控制为例[15],每个控制步都要多次调用正运动学计算过程作为预测模型进行MPC的优化计算.因此,无论是开环控制(逆运动学),还是闭环控制,正运动学的计算效率直接影响同心管机器人控制算法的实时性.本文的主要创新点为,提出了一种解析和数值相结合的同心管机器人正运动学快速求解方法.该方法无需额外力矩传感器,相比传统两步积分法,计算时间大大减少.

本文的主要工作如下:首先,提出了一种同心管机器人正运动学快速求解方法.该方法基于机器人几何学,使用一种解析和数值相结合的方法计算末端点的空间位置,在损失有限精度的情况下,大大提高了正运动学的计算效率.其次,基于正运动学方法,给出了同心管机器人的逆运动学求解方法.再次,利用仿真研究,验证了提出的正运动学快速求解算法的有效性.仿真结果表明,提出的快速方法相比两步积分法,正运动学的计算时间从3.5×10−2s减少到5.6×10−4s,误差增加的均值为0.66 mm;逆运动学的计算时间从0.95 s 减少到1.8×10−2s,误差增加的均值为0.0112 mm.最后,利用实验研究,验证了提出的快速求解方法在实际应用中,相比两步积分法,只损失了有限精度(实验中正逆运动学求解的计算时间与仿真中相同,所以实验研究只关注误差).实验结果表明,提出的快速方法相比两步积分法在正运动学的求解中误差增加了0.029 mm;在逆运动学的求解中误差增加了0.103 mm.

本文的主要内容安排如下:第2节给出了同心管机器人的数学模型,一种正运动学快速求解方法和对应的逆运动学方法;第3节在快速算法的基础上,对同心管机器人的模型进行仿真计算,验证了本文方法的快速性和有效性;第4节则利用实物研究,分析比较了本文方法与传统方法在实际应用上的误差损失.

2 同心管机器人的数学模型

同心管机器人通常由多根具有记忆功能的超弹性镍钛合金预弯管相互嵌套而成,如图1所示.每根管有两个相互独立的输入自由度(轴向旋转与伸缩),管间的弹性作用能够使其在狭窄的空间中灵活运动.

图1 同心管机器人实物Fig.1 Concentric tube robot

2.1 建模前的假设及描述

同心管机器人的建模主要基于一种特殊的Cosserat杆模型[10],且需满足以下假设:1)忽略截面处的剪切应变及管的轴向伸长;2)忽略管间摩擦及自身重力对建模的影响;3)末端不受外力作用[5,13].同心管相互嵌套的三维结构如图2所示,其内部点划线代表管的中心线.图中的W(0)为定义在同心管原点处的世界坐标系,该坐标系的Z轴与管的中心线相切并指向管的末端,将W(0)沿中心线向末端滑动且不做绕Z轴的旋转,可得同心管弧长s处的世界坐标系W(s).将W(0)绕Z轴旋转θi(0)可得到每根管在原点处的体坐标系Bi(0),下标i=1,2,···,N为镍钛管的编号,且本文规定最内管的编号为1.同理将Bi(0)沿中心线向末端滑动能够得到弧长s处的体坐标系Bi(s).r(s)=(x,y,z)为同心管上某点相对于原点的位置坐标,R(s)则为其对应的旋转矩阵[13].

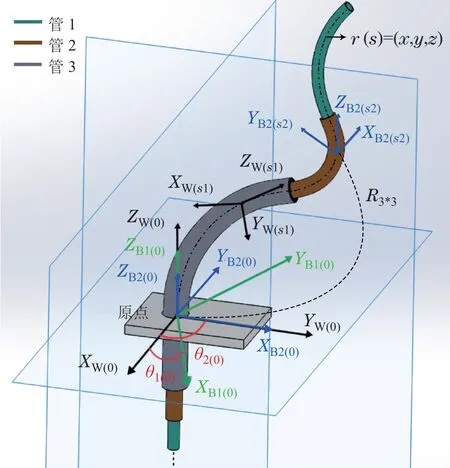
图2 同心管三维结构示意图Fig.2 Three-dimensional structure diagram of concentric tube robot

接下来通过同心管驱动端的侧视图来进一步解释机器人的输入变量[16]:对于由镍钛管组成的同心管机器人来说,每根管有两个相互独立的控制输入:θi和ϕi分别为同心管驱动端的旋转输入和伸缩输入,且本文规定ϕi >0,θi(−ϕi)=θi(0).

ui(s)和vi(s)分别为同心管在运动过程中每单位弧长的角应变率(曲率)和线应变率向量,其中x,y分量是由管的弯曲引起的,而uiz(s)则是管的扭转造成的,且世界坐标系和体坐标系上同一点处的曲率可通过下式实现转化:

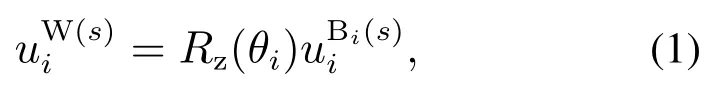
Rz(θi)为绕Z轴的旋转矩阵,而因为忽略了管的剪切应变和轴向伸长

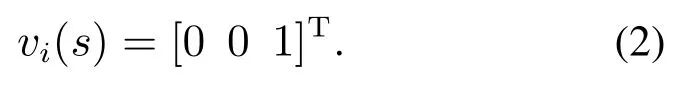
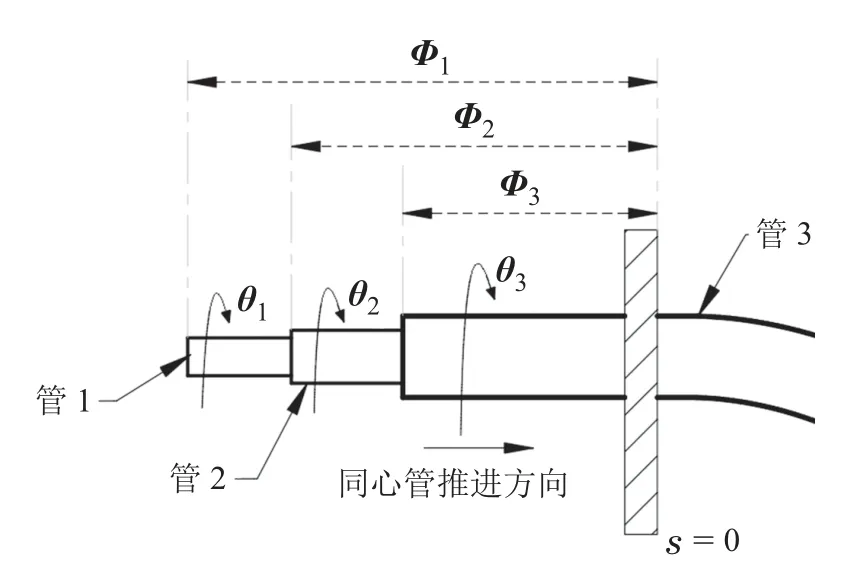
图3 同心管机器人输入量示意图Fig.3 Inputs diagram of concentric tube robot

为了建模及计算的方便,本文将满足分段常曲率的同心管机器人正运动学解耦为两步映射[17],如图4.图中的q(t)=[θi ϕi]为t时刻各管的输入量,F1为从驱动空间到曲率空间的映射,F2为从曲率空间到任务空间的映射.

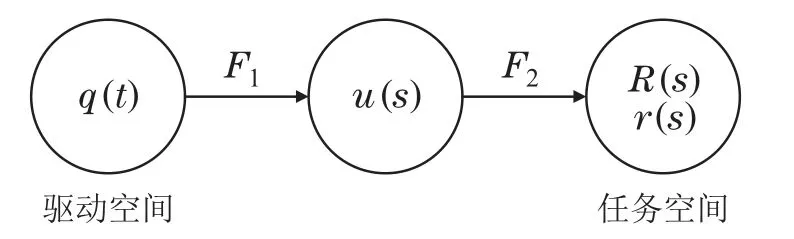
图4 同心管机器人正运动学映射Fig.4 Forward kinematics mapping of concentric tube robot

2.2 刚性模型和柔性模型

是否考虑扭转是区分刚性模型和柔性模型的关键,而由于考虑了扭转,后者的精度要更高.下面将首先对这两种模型的F1映射作简单介绍[5],在第2.1节的基础上,需要进一步作以下规定:1)以下讨论都是基于静态的;2)同心管在嵌套完毕后,每根管在同一弧长处的曲率相等

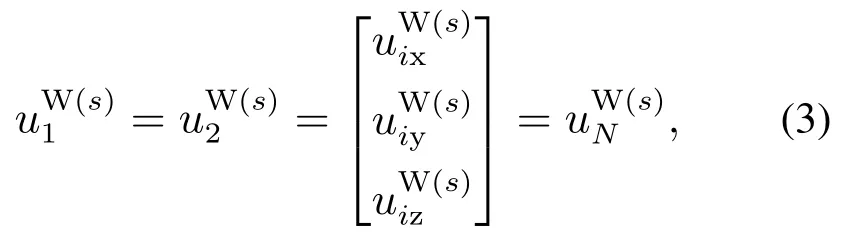
3)任意截面上的净力矩恒为零:

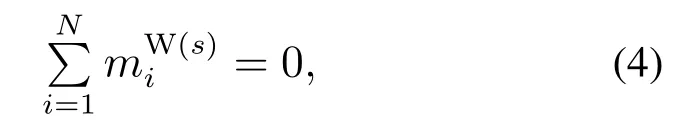
其中mi为管弯曲产生的力矩;4)管在弯曲过程中产生的力矩和曲率成线性关系:

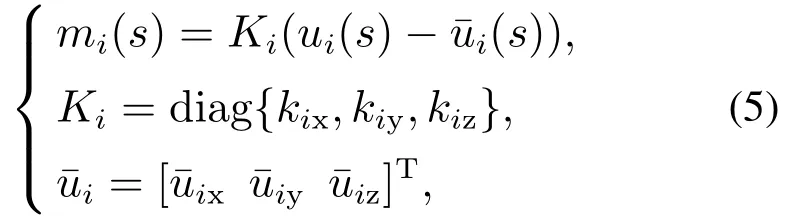
首先考虑刚性模型,因为忽略了扭转对建模的影响,故各管Z方向的曲率恒为零,即uiz(s)≡0,从而导致每根管任意弧长s处的旋转量恒等于旋转输入的大小:θi(s)=θi(0).因此,根据式(1)–(5)可得各管在世界坐标系下的曲率

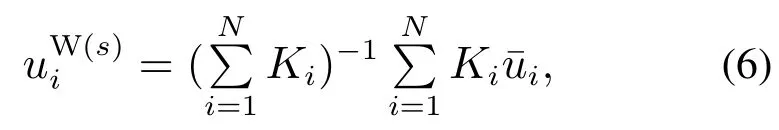
刚性模型的F1映射能够直接通过解析的方法求得,但由于没有考虑扭转,无法很好地描述同心管机器人的运动,因此必须把扭转引入到建模中.

考虑柔性模型,定义αi(s)为管i与管1的旋转角度之差

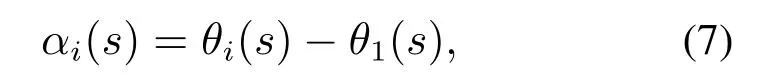
进一步可得到同心管嵌套后各管的弯曲曲率

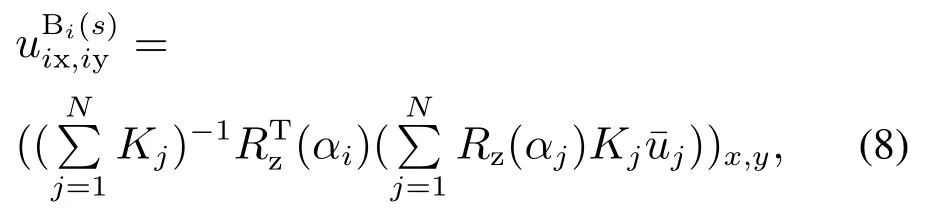
根据Cosserat杆模型以及式(5),可得到同心管扭转和曲率的关系式

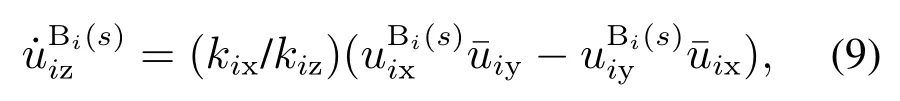
其中“·”表示变量关于弧长s的微分,而旋转角度θi和扭转曲率uiz的关系为

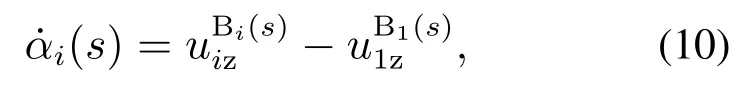
式(8)–(10)为一系列可解的微分方程,对应的边界条件为

1) 输入:αi(0)=θi(0)−θ1(0);

2) 同心管末端不受外力:uiz(Li)=0,Li表示管i在s>0部分的长度.

这是一个两点边值问题(two point boundary value problem),通过求解就能获得管i在其体坐标系Bi(s)中的曲率向量ui(s),更多与模型相关的介绍详见文献[5].

2.3 同心管机器人运动学稳定性分析

由于同心管在建模时的不确定性,导致其会因为弯曲和扭转的积累造成弹性势能的迅速释放,使同心管在运动过程中出现多解问题,即从当前平衡点迅速跳跃到另一个平衡点[18],这在实际应用中是很危险的.

在不限制管的数量及曲率的情况下,很难对同心管的该现象进行分析[16],大多数研究都通过提前设计参数的方法使机器人避免发生分岔.文献[18]给出了管数确定的常曲率同心管机器人的稳定性解析条件(以3管为例):

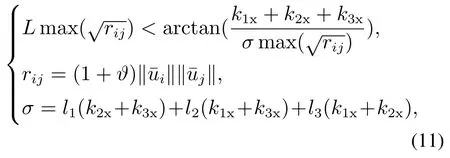
其中:L为管弯曲部分的长度,i,j表示相邻管的序号,li为第i根管直线段部分的长度.在机器人实际的应用中,需设置好相关参数,避免其发生运动学不稳定.

2.4 同心管机器人正运动学的快速求解算法

考虑图4的F2映射,本文主要讨论其中位置坐标r(s)的映射.因为同心管相互嵌套后满足式(3),而同心管机器人最内管是最长的,且只有当其从外管中伸出后,才能够完整的观察到CTRs在自由空间中的运动状态,故本文只需考虑管1的曲率.若没有特别指明,以下讨论都是在体坐标系B1(s)内进行的.基于已求得的曲率u1(s),一般可通过两步积分法获得任务空间中的位姿信息[5,13]

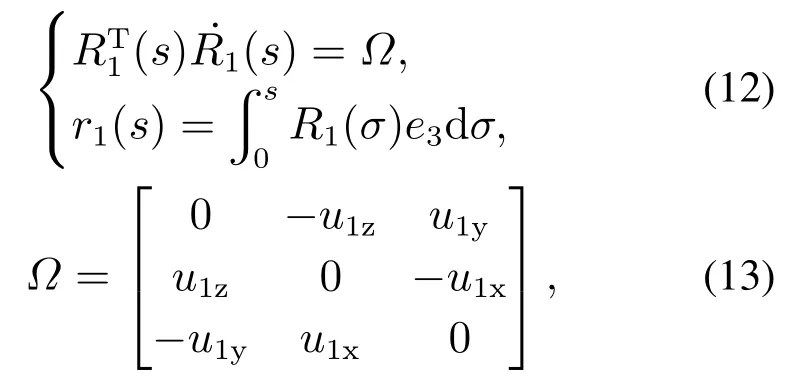
其中:Ω为曲率向量u1(s)的反对称矩阵,e3为Z方向的单位向量.目前,几乎所有的工作都使用式(12)计算在当前输入q(t)下,同心管机器人在任务空间中的位姿信息[5–9],该方法能够达到较可观的精度,但因为这是一种纯数值方法,计算时间较长,不利于机器人的实时运行;为了提高计算速度,文献[14]提出了一种快速柔性扭转机器人模型,通过引入全局变量,建立了欧拉角与曲率的关系式,使计算机能以毫秒级的速度计算出当前的位置信息,但该方法需借助力矩传感器来实时获取扭转力矩,该方法最终使用电磁跟踪器得到2管机器人的误差均值为3.2 mm.

为了提高计算速度,并且避免使用传感器提供初值信息,本文提出了一种解析和数值相结合的同心管机器人F2映射计算方法,该方法能在牺牲有限精度的情况下大幅提升计算速度.在进行所提方法的数学推导之前,由于F1映射得到的曲率u1(s)是基于当前体坐标系B1(s)的,需先将其从B1(s)转换到对应的基坐标系B1(0),使不同弧长s处的曲率参考系相同

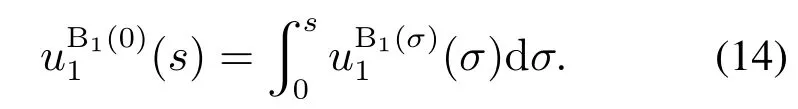
假设同心管在自由空间中的运动为刚体运动,根据李代数理论可知,空间曲线上某点关于原点的齐次变换矩阵和该点关于弧长s的瞬时角速度分别为

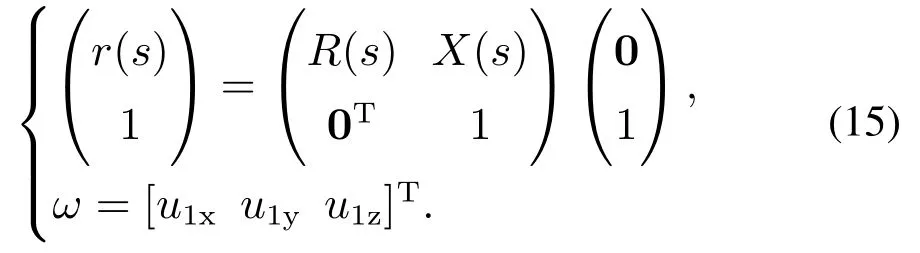
对于任意的平移算子X(s),始终满足ΩX=ω×X,其中×代表向量间的叉乘.对于刚体上某点的瞬时螺旋运动,本文只考虑平移变换,即R(s)为单位矩阵时,有r(s)=X(s),则刚体上该点的速度为[19]

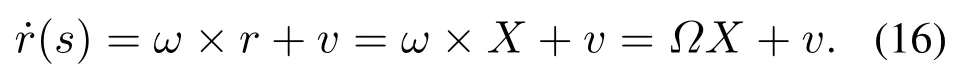
而满足分段常曲率特性的连续机器人齐次变换矩阵为[17]

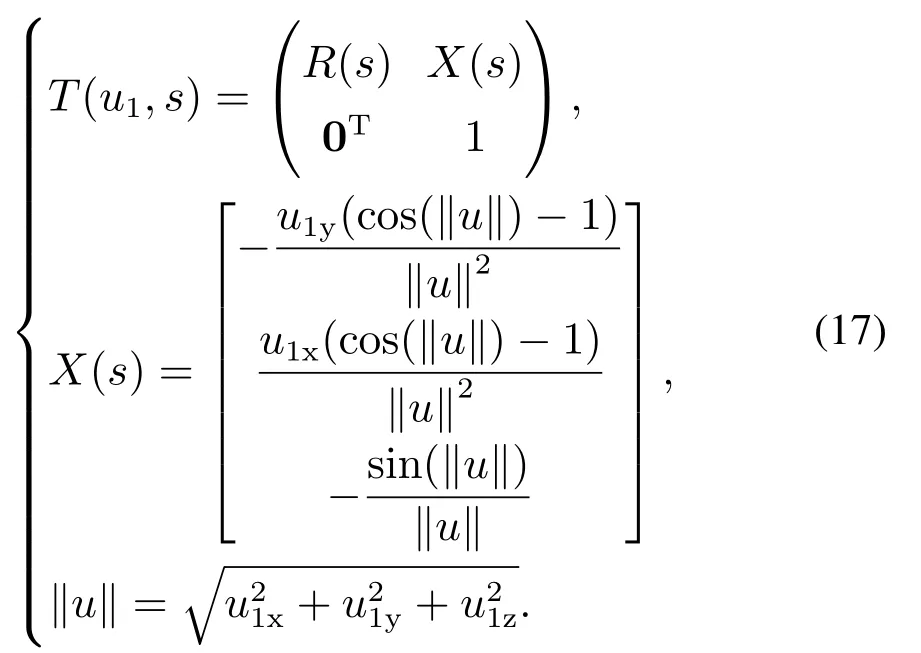
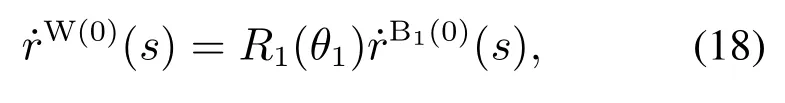
2.5 同心管机器人逆运动学分析

基于图4的同心管机器人两步映射,机器人末端点的位姿可通过下式进行计算[21]

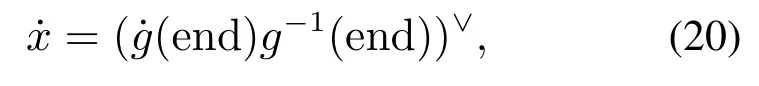
其中:g(end)∈SE(3)表示机器人末端点相对原点的齐次变换矩阵,()∨则表示从4×4的矩阵中提取出6×1的末端点速度信息[19]

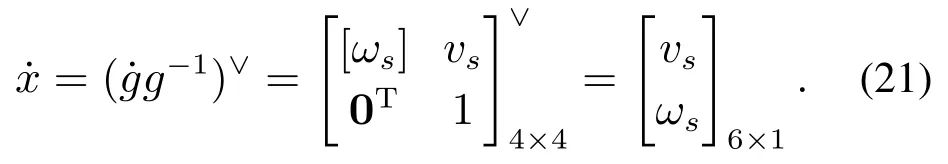
上式中省略了弧长位置end,vs和ωs分别表示机器人末端点的瞬时线速度和角速度.对于逆运动学问题,g的瞬时微分可以由期望位置的齐次变换矩阵gt与当前齐次变换矩阵gc的差值代替式(22),并且以上两个齐次变换矩阵中的位姿信息可以通过正运动学模型(12)和式(16)–(17)在计算过程中求得.

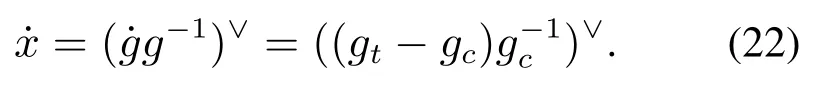
接下来考虑雅可比矩阵J的计算,针对连续型机器人,可以使用下式计算雅可比矩阵[22]

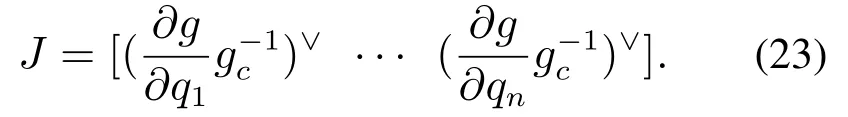
同式(22)的处理方式一致,本文使用有限差分来近似g的瞬时微分,得到近似的雅可比矩阵J的每一列

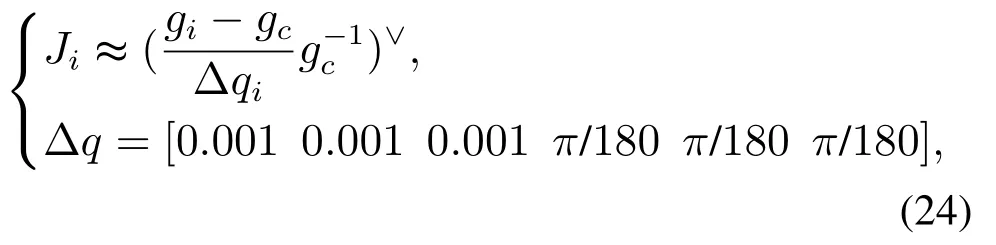
其中:i表示列数,gi相当于关节输入量为q+∆qi时对应的齐次变换矩阵.这样对于3管6输入的机器人来说,可以得到大小为6×6的雅可比矩阵J.

这样就可以根据式(19)进行同心管机器人的逆运动学计算,在计算过程中,还需根据雅可比矩阵是否满秩选择不同的迭代更新方式进行逆运动学的求解:当J满秩时,使用如下方式计算:

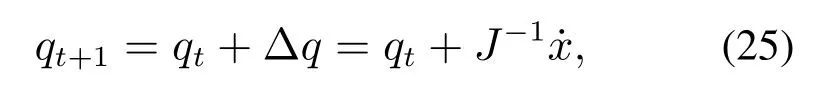
其中:t为迭代次数,q0表示初始的输入;而当J不满秩时,采用下式进行求解:

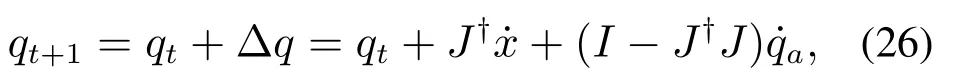
其中:J†为雅可比的伪逆,为任意输入量的变化量.

3 同心管机器人运动学仿真实验

3.1 正运动学仿真

接下来首先借助仿真实验对所提出方法的快速性进行验证.主要使用刚性和柔性这两种不同的运动学模型进行验证,同心管几何参数如表1所示.

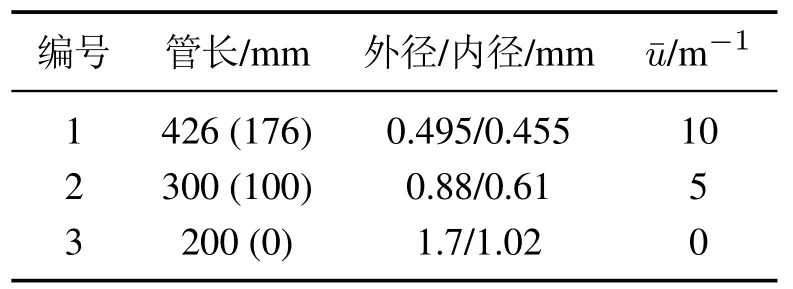
表1 同心管机器人几何参数Table 1 Geometric parameters of concentric tube robot

表1中的管长表示每根镍钛管的总长度,()内为对应的弯曲部分长度.外径和内径指管截面圆环的半径.本文材料的杨氏模量E为70 GPa,根据泊松比ϑ=0.33可计算出剪切模量G约为26 GPa.由文献[11]可知,对任意两根相邻的超弹性管来说,若外管和内管的刚度比大于6,则CTRs满足刚度主宰的要求,使其以FTL的方式运动,减少了不必要的干扰.由刚度计算公式k=EI可知,所采用的同心管满足上述要求,根据式(11)及表1的参数,可知本文设计的同心管机器人不会发生第2.3节的运动学不稳定.

首先根据表1参数以及机器人的正运动学,绘制出同心管机器人的可达工作空间,如图5所示.

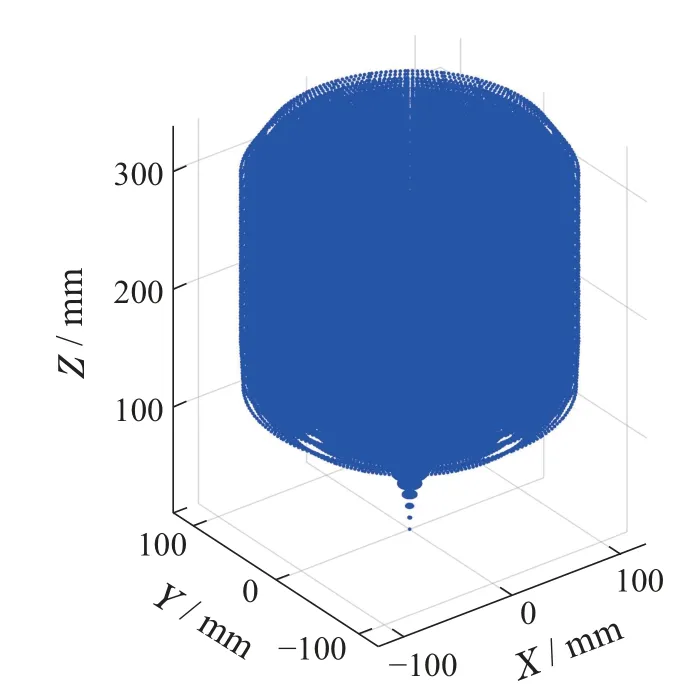
图5 同心管机器人工作空间Fig.5 Workspace of concentric tube robot

在仿真中,主要使用两步积分法和本文方法计算不同运动学模型的末端位置,并记录所花的时间,且仿真中以两步积分法得到的结果为参考值.因为管的扭转对机器人的运动学建模精度有一定的影响,故在仿真中将所有管的伸缩量以及管3的旋转量都设为定值,而将管1管2的旋转输入量设置为固定区间内的等间隔采样,具体见表2.

表2 同心管机器人仿真输入参数Table 2 Simulation input parameters of concentric tube robot

如表2所示,选择以上伸缩输入量的目的是使每根管都能从其相邻外管中伸出,从而完整地表现出同心管的运动状态;等间隔采样是指在区间上以相同间隔取出n个数,设由这n个数组成的集合为P,则管1管2的旋转输入集为

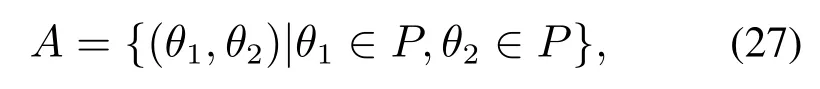
即共有n2种不同的输入.需要注意的是:本文在使用MATLAB数值求解式(12)及式(14)时,采样点个数m的多少会影响计算速度和精度,但其对两种方法的影响是等价的.

因为仿真的目的是为了证明所提出方法相比两步积分法的快速性,若将m取的过大,反而会影响整体的计算效率(当m超过一定值后,其对计算精度的影响已可以忽略不计,但计算时间却仍随着m的增大而增加).本文设n和m分别为1000和2000,最终可得到如表3的仿真结果.

表3 所提方法与两步积分法的性能比较Table 3 Comparison of performance between the proposed method and the two-step integration method

表3中的eavg指在相同输入下,使用本文方法计算得到的同心管末端位置坐标相对于参考值的误差均值,且误差的中位数分别为0.339 mm和0.634 mm,而产生误差的主要原因是所提方法将同心管在自由空间中的运动视为了刚体运动.t2和t3分别指使用两步积分法和本文方法计算F2映射的时间均值,这里导致两种方法计算时间都相对较短的原因是采样点m取的较少(当m取到20万时,单次仿真下两步积分法的计算时间将达到1.8 s以上).以上仿真实验在处理器为Intel i7-6800 k 3.4 GHz,运行内存为16 G的Win10操作系统上使用MATLAB 2018b完成.仿真效果图如下:图6展示了相同输入下,使用本文方法计算得到的同心管末端位置坐标相对于参考值的误差;图7展示了相同输入条件下,本文方法和两步积分法计算F2映射所需的时间.

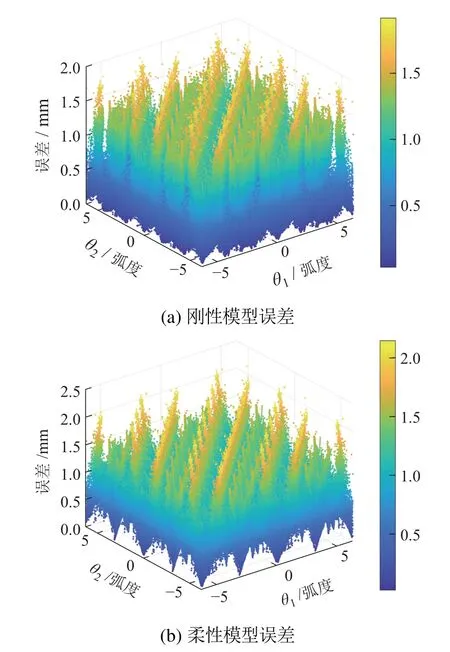
图6 正运动学计算误差Fig.6 Error of forward kinematics calculation

根据表3及图6和图7,可以获得以下结论:1)本文方法会在计算精度上造成一定的损失,但由平均误差及误差中位数可知,误差损失在可接受的范围内;2)本文方法在计算速度上相比两步积分法有了一定程度的改善,利于机器人系统的实时运行;3)本文所提出的方法既适用于刚性模型又可在柔性模型上达到可观的效果.本文会通过第4节中的实验进行末端点实际位置与模型计算位置的误差大小测试.

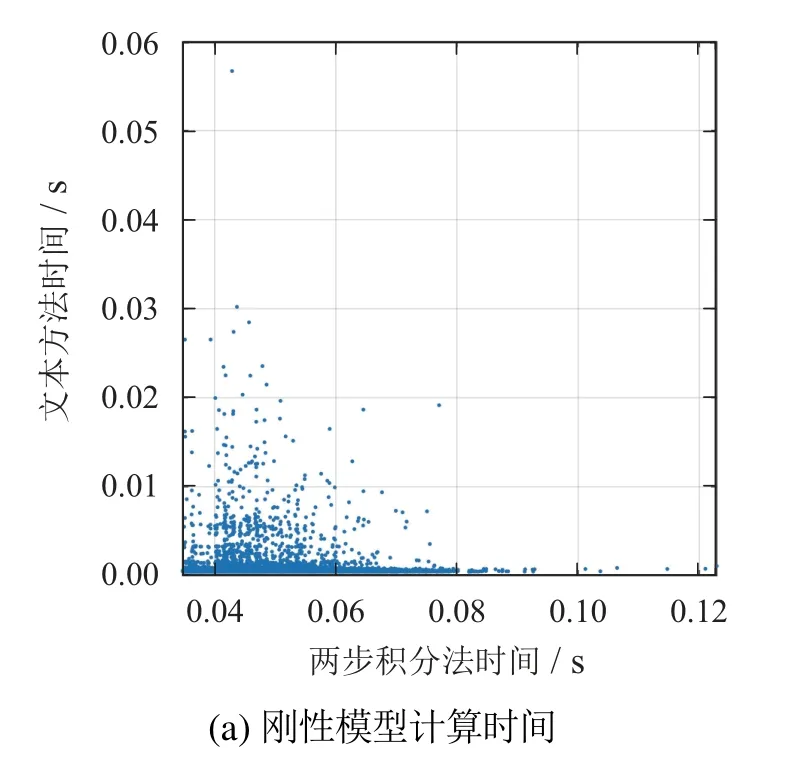
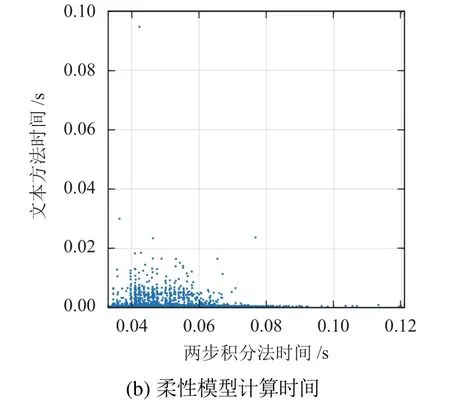
图7 F2映射计算时间Fig.7 Mapping computation time of F2

3.2 逆运动学的仿真实验

为了验证逆运动学以及本文所提正运动学方法的有效性和快速性,本文任取300个满足输入限制(ϕ1>ϕ2>ϕ3>0)的Q构成期望输入集Qt(目的是保证期望位置是在机器人可达工作空间内的),并根据两步积分法式(12)和本文方法式(16)–(17)提前计算出第k个期望输入Qtk对应的姿态Rtk和末端位置rtk,用作构成期望的齐次变换矩阵gt.

本文使用与正运动学仿真完全相同的参数和机器人的柔性建模方式,并分别使用两步积分法式(12)和本文方法式(16)–(17)计算当前时刻末端点齐次变换矩阵gc(两种方法都使用式(12)计算姿态信息,位置信息则使用不同的方法计算),然后针对不同的期望输入,选择不同的初始输入估计,使用第2.5节的方法进行逆运动学的计算.实验结果如图8–10所示.

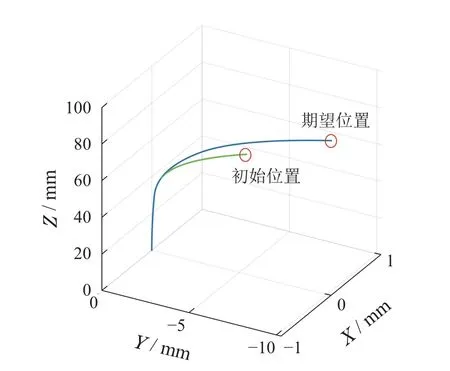
图8 同心管机器人逆运动学示意图Fig.8 Inverse kinematics diagram of concentric tube robot

图8为逆运动学求解前后的同心管状态示意图,机器人可以从初始位置顺利移动到期望位置;图9展示了300次仿真实验中,将逆运动学求解得到的结果代回到模型中计算得到的实际位置rk与期望位置rtk的误差;图10展示了使用不同方法计算逆运动学的时间,即为基于逆运动学的开环控制时间开销.逆运动学具体计算结果如表4所示.

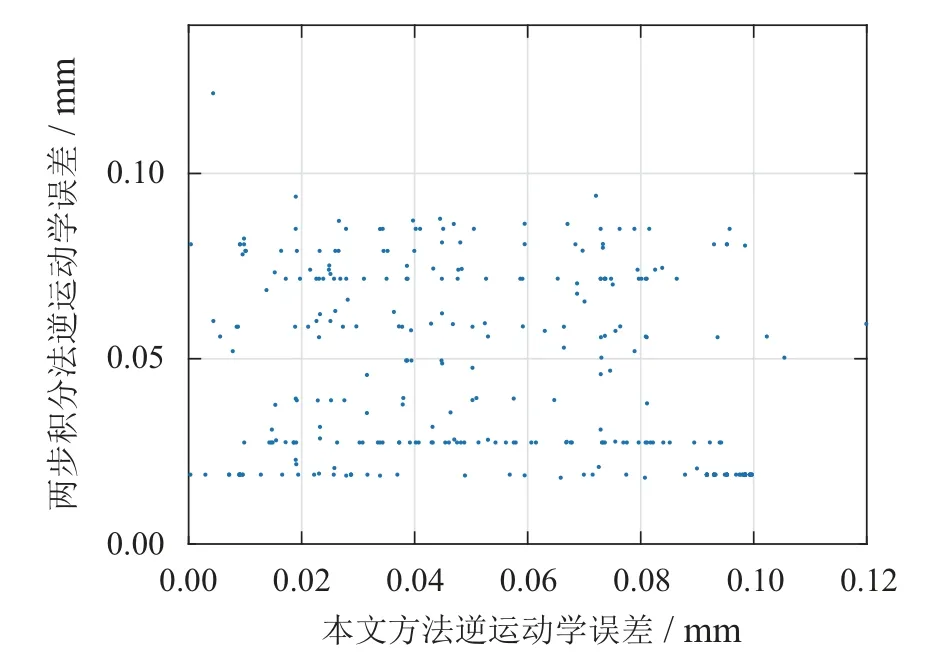
图9 逆运动学求解误差Fig.9 Error of inverse kinematics solution

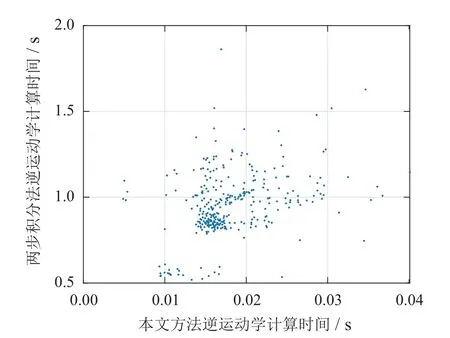
图10 逆运动学求解计算时间Fig.10 Computation time of inverse kinematics solution

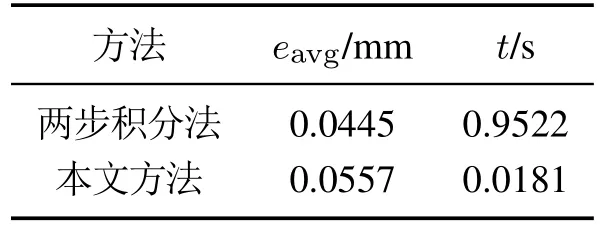
表4 逆运动学计算结果比较Table 4 Comparison of inverse kinematics calculation results

表中eavg为图9误差的平均值,根据表中数据可知,使用本文方法计算得到的逆运动学仿真误差略大于两步积分法,接下来会在第4节的实验中对实际误差进行测试;t为使用两种方法进行逆运动学求解的平均时间,可见本文方法在计算时间上有了很大的提升,而计算时间相对表3的单次正运动学增加的原因主要为逆运动学计算过程中需要多次使用正运动学模型.

4 实验验证

接下来通过实物实验测量末端点实际位置与模型计算位置的误差大小.

4.1 正运动学模型验证实验

实验平台如图11所示,使用视觉传感器Kinect2搭建立体相机系统来获取同心管机器人末端点的空间位置.因为Kinect无法获得面积过小物体的深度值,故本文在同心管末端固定泡沫标记点进行间接测量.驱动系统主要由6个内含运动控制器的步进电机组成,分别驱动3根管的伸缩和旋转,可以达到精确平滑的位置控制需求.

图11 同心管机器人实验场景及实验设备Fig.11 Experimental scene and equipment of concentric tube robot

本文通过相机支架将Kinect与同心管末端的距离保持在1 m以内,使其深度测量误差在4 mm以内[23],并通过标定获得深度摄像头的内外参,最后通过刚体变换T将世界坐标系从标定板变换到机器人原点处.同心管实物的参数与表1相同.本文进行了300组不同输入下的实物验证,记录了机器人末端点的空间位置,并与正运动学的计算结果作对比.因为这里主要是计算本文方法的位置误差,故本文选择更精确的柔性模型进行对比.实验结果如图12所示.

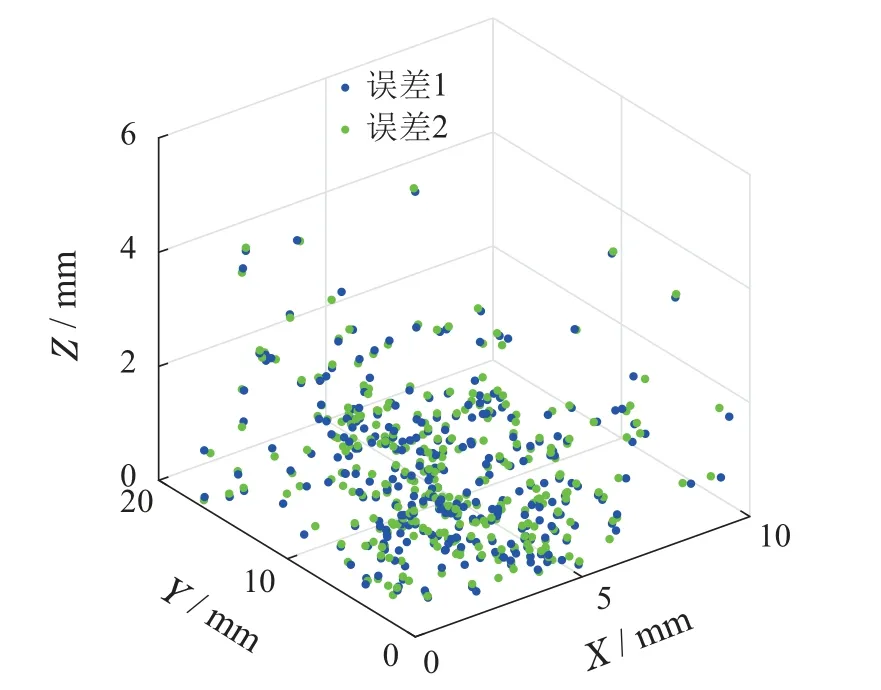
图12 实测误差Fig.12 The measurement error

图12中的error1和error2分别为使用两步积分法和本文方法得到的同心管末端点坐标与实测值的误差绝对值.而通过图12,还可以计算出模型与实测值各坐标分量误差的均值和总误差的大小,见表5,可见本文方法的实际误差相比两步积分法增加了0.029 mm.

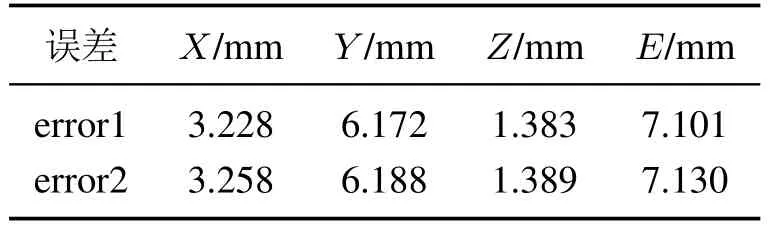
表5 实测误差的平均值Table 5 The mean value of the measured error

4.2 基于逆运动学的开环控制误差测量

本文从第3.2节中选取传统方法和本文方法在相同期望下的100组逆运动学计算结果,将其作为输入信号送入电机驱动系统,并在相同的实验环境下使用Kinect测量出机器人末端点的空间位置,实验结果如表6和图13所示.

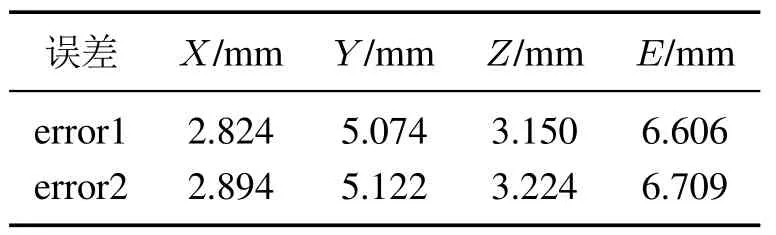
表6 逆运动学开环控制误差Table 6 Inverse kinematics open-loop control error

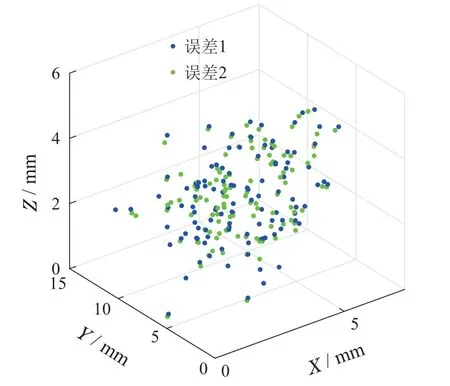
图13 开环控制实验结果Fig.13 Open-loop control experiment results

图13记录了基于逆运动学的开环控制实际位置与期望位置的误差(error1和error2分别为使用两步积分法和本文方法的开环控制误差).表6为坐标分量误差的平均值,E为总误差,可见基于本文方法的逆运动学实际误差相比两步积分法增加了0.103 mm.

4.3 实验结果分析

由以上实验结果可知,坐标误差主要出现在Y分量上,而由相机的外参定义可知,Y分量对应于机器人末端在相机坐标系中的深度值Zc[24].因为Kinect传感器本身有4 mm左右的深度测量误差,且末端标记点有厚度(实验中手动调节使末端位于标记球的球心),故在Y轴方向会出现较大的误差.除去以上主要的误差来源外,还需考虑以下因素:1)机器人建模误差;2)相机外参矩阵计算误差及相机镜头的畸变;3)刚体变换T的估计误差;4)从Kinect红外图中获取标记点球心坐标的误差;5)机器人回零误差.

综合考虑所有误差来源,并与传统方法的实验结果作比较:在相同的实验平台下,两种方法的绝对误差较大,但本文方法相比传统方法误差仅增加了0.1 mm(相对误差小).因此可得出本文方法与传统方法相比精度损失不大.

5 结论

针对同心管机器人计算成本过大的问题,本文基于机器人几何学,提出了一种解析和数值相结合的正运动学求解方法,能在不同的模型上表现出更快的计算效率.首先给出了所提方法的数学推导,然后基于正运动学的快速求解方法,给出了同心管机器人的逆运动学求解方法;再利用仿真研究,验证了提出的正运动学快速求解算法的有效性;最后利用实验,验证了提出的快速求解方法在实际应用中,相比两步积分法,只损失了有限精度.本文所提方法适用于同心管机器人的运动学快速计算,后续工作将针对减小系统误差,提高鲁棒性等方面进行深入研究.