船舶目标重叠下马赛克图像数据增强方法研究

曾广淼 俞万能 王荣杰 林安辉

(1.集美大学轮机工程学院,福建厦门 361021;2.福建省船舶与海洋工程重点实验室,福建厦门 361021)

1 引言

目前随着计算机技术的迅速发展,图像识别技术不只停留在实验室中,在社会上的各个领域均得到了广泛的应用,而亟待解决的海面目标识别问题就是其中之一,作为船舶智能航行技术发展中的重要一环.近年来,对于海面目标的识别方法有很多,大部分是通过合成孔径雷达得到的海面遥感图像,Guo等人对CenterNet的网络结构进行了改进,提升了船舶小目标的识别能力[1],Li等人提出了新的双分支回归网络,提升了船舶的定位能力[2],Fu等人利用特征平衡与细化网络的无锚框方法,提升了复杂场景的船舶检测能力[3].上述文章都是以垂直视角对海面船舶目标进行识别,且需要借助飞机、卫星等航空器进行拍摄,而搭载在船舶上以水平视角对周围海面目标进行识别的相关研究较少.

不仅如此,大部分研究都对小目标的识别问题进行了讨论,这考虑到了宽阔的水域中的视野相对较远的情况,但是,船舶还存在处于狭窄水域航行的情况,此时周围船舶较多,在观测视野中极易出现相互遮挡的现象,因此,快速准确地将不同重叠程度目标进行识别定位的问题就成为重点之一.对于遮挡目标的识别问题,国内外已有一定的研究成果,Wan等人通过生成对抗网络将局部面部特征进行恢复,从而实现遮挡情况下的人脸识别[4],Chowdhury等人将渐进式扩展算法与图注意力网络相结合,提高街道拥挤状态下的车牌识别能力[5],Liu等人利用耦合网络来提升小目标或被遮挡行人的识别准确率[6].他们通过对神经网络进行优化,提升了对遮挡目标的识别能力,由于对网络结构进行了的加强,或多或少地增加了计算复杂度,降低了目标识别的检测速度.

现阶段,目标检测方法主要分为两种,第1种为以R-CNN系列[7–10]为代表的二阶段检测方法,其首先利用区域提议网络提取感兴趣区域,然后基于感兴趣区域的大小,从上到下,从左到右遍历测试图片进行识别与检测.第2种为以SSD[11]、YOLO系列[12–15]为代表的一阶段检测算法,其不依赖区域提议网络,而直接利用锚框,将测试图片分割成的多个方格区域,对每个区域分别进行识别与检测.相比之下,二阶段方法更准确但会产生一定量的冗余计算.一阶段方法在牺牲一部分准确率的情况下,大大提高了检测速度,有利于满足实时监测的需要.

Yolov4算法[15]将作为实验的基本模型,虽然其提出的时间较短,但是已经在农业[16]、建筑业[17]、医学[18]等领域得到了一定的应用.上述文献中的实验都是利用部署于陆上服务器进行训练与测试的,情况不同是,海上的通信信号相对不稳定,且由于海况复杂,需尽量减小识别系统的体积与能耗,因此需要考虑到检测系统处于离线使用的情况.因此在本文中选择Yolov4–tiny轻量级算法作为主要的实验模型.

基于以上分析,本文提出了一种改进的马赛克(Mosaic)数据增强方法,主要贡献可以总结如下:

1) 对训练数据集中的图像进行数据增强,在不改变网络结构的情况下,加强目标识别算法对船舶重叠目标的识别能力.

2) 针对处于离线状态下的小型移动平台,选择合适的轻量级算法,在保持其识别速度的情况下提升识别准确率,降低不同分辨率的输入图像对算法识别性能的影响.

3) 通过在船舶数据集不同的海域进行实时检测测试,结果表明,经过改进Mosaic方法训练后的算法在船舶重叠目标的检测当中准确率更高,证明了改进方法的有效性和鲁棒性.

本文的剩余部分安排如下:第2节详细介绍了改进Moasic方法与Yolov4–tiny算法的主要结构;第3节描述了仿真实验比较及实测实验结果;最后在第4节中得出结论.

2 方法论

Yolo[12]算法自2016年首次提出以来受到了广泛的关注,而随后提出的Yolov2[13]和Yolov3[14]算法在其基础上对模型结构、数据预处理方式、损失函数计算方法进行了一系列的改进,极大提升了目标检测的速度与准确率.而Yolov4算法在Yolov3算法的计算方式上,增添了很多优化技巧,在识别速度不变的情况下提升了识别准确率.

2.1 Yolov4–tiny算法的概述

Yolov4–tiny网络是基于Yolov4网络进行简化,在牺牲一部分识别准确率的情况下,减少了10倍的参数量.从Yolov4网络中约6000万的参数降至Yolov4–tiny中约600万的参数.其网络结构图如图1所示.

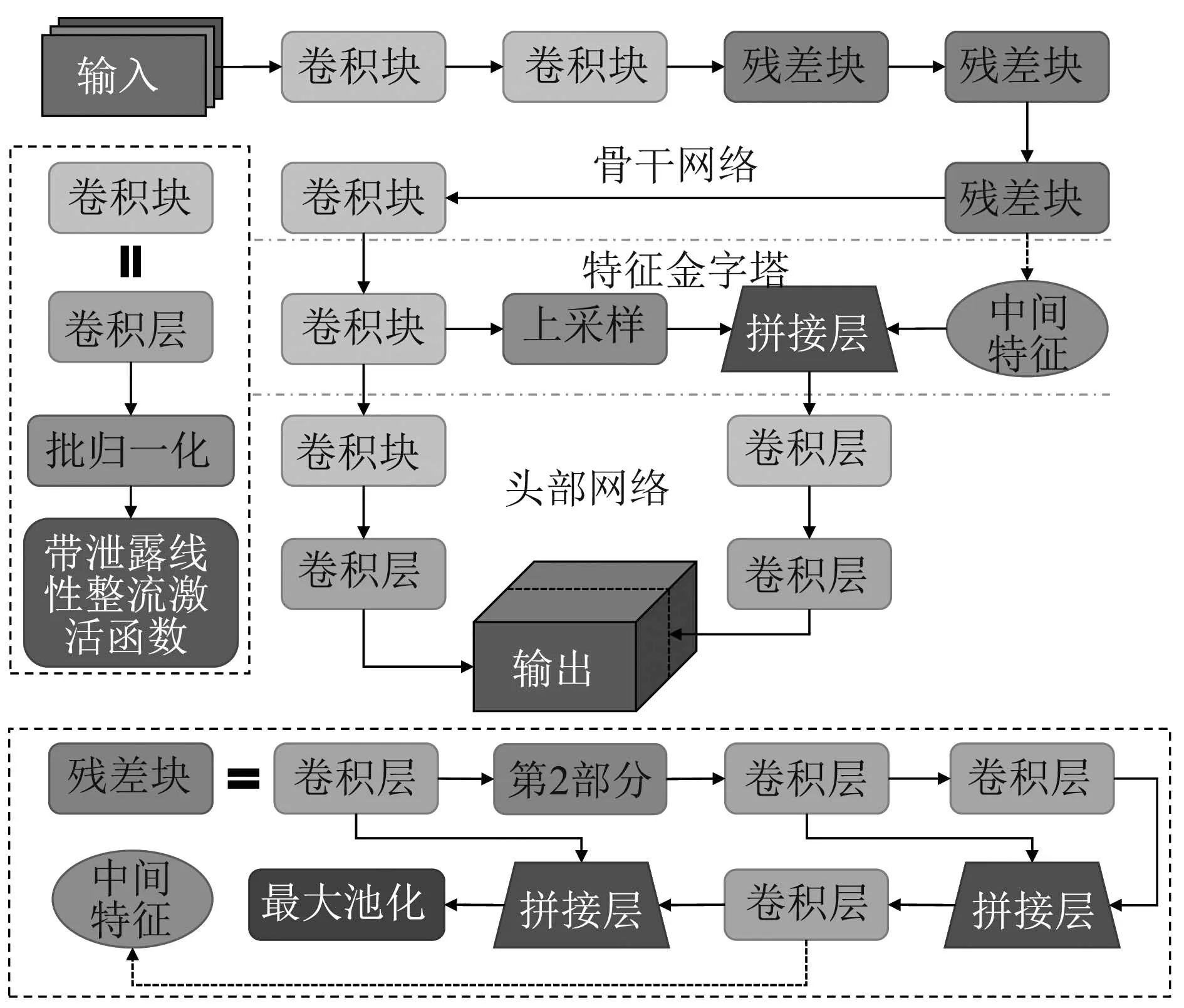
图1 Yolov4–tiny网络的特征结构Fig.1 Characteristic structure of Yolov4–tiny network

其中,骨干网络中的卷积块由卷积层、批归一化层[19]、带泄露线性整流[20]激活函数组成.而残差块是融合了跨阶段局部网络[21]思想(CSPNet)的CSPDarknet53-Tiny,其结构如图2所示.

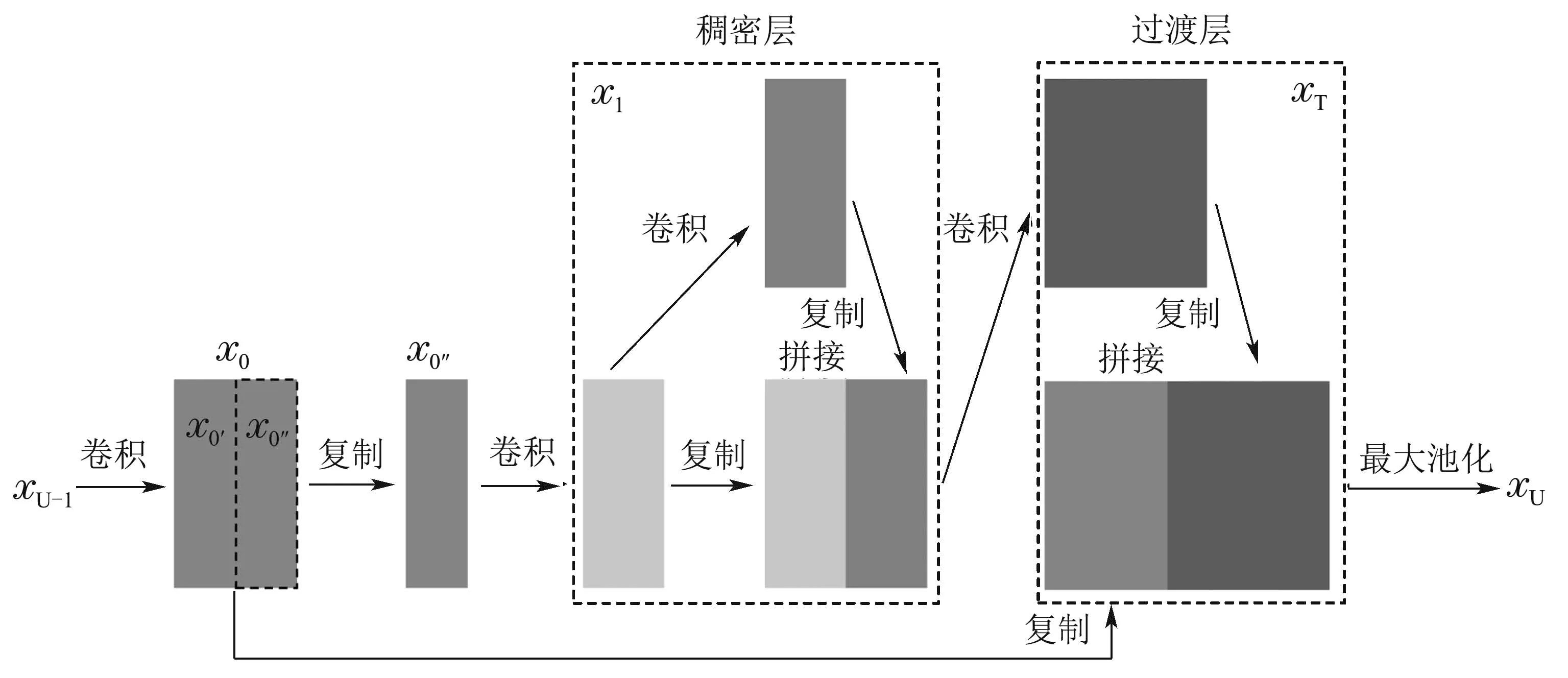
图2 CSPDarknet53-Tiny网络中残差块的结构示意图Fig.2 Structure of residual blocks in CSPDarknet53-Tiny networks

它由稠密层和连接层组成,首先对上一卷积层的输出xU−1进行卷积操作,生成新的卷积层,将其输出x0=[x0′,x0′′]分成前后两个部分x0′和x0′′进行前项计算,在Yolov4–tiny的网络结构中,先取第2部分进行前项传播,再将第1部分与第2部分一起直接连接到阶段的末尾,跳过稠密层,等到第2部分的x0′′完成前项计算之后在过渡层中与x0进行特征拼接,得到输出xT,其经过最大池化后产生残差块的输出xU.残差块前向计算与反向传播的过程如式(1)–(2)所示:

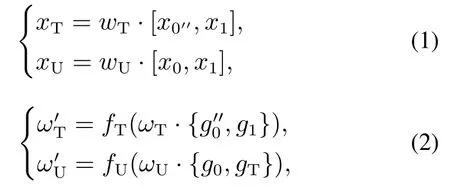
其中:ωi和是前向计算与反向传播时的权重,fi表示权重更新的函数,gi表示传播到第i层的梯度,i等于T或U,分别代表着连接层或残差块的输出.所以,利用跨阶段局部网络的结构在反向传播时,可以将不同通道上的梯度分别进行积分,比如,梯度信息经过稠密层时,只会改变x0′′通道上的权重却不会影响到x0′.从而在保留不同深度的特征值的同时,减少了过多的重复梯度信息,在不影响网络特征提取效果的情况下,减小了内存的开销,提高了网络的运算速度.

在骨干网络之后,利用特征金字塔结构[22]对网络特征进行优化,Yolov4–tiny网络中小型特征金字塔的实现方式如图3所示.

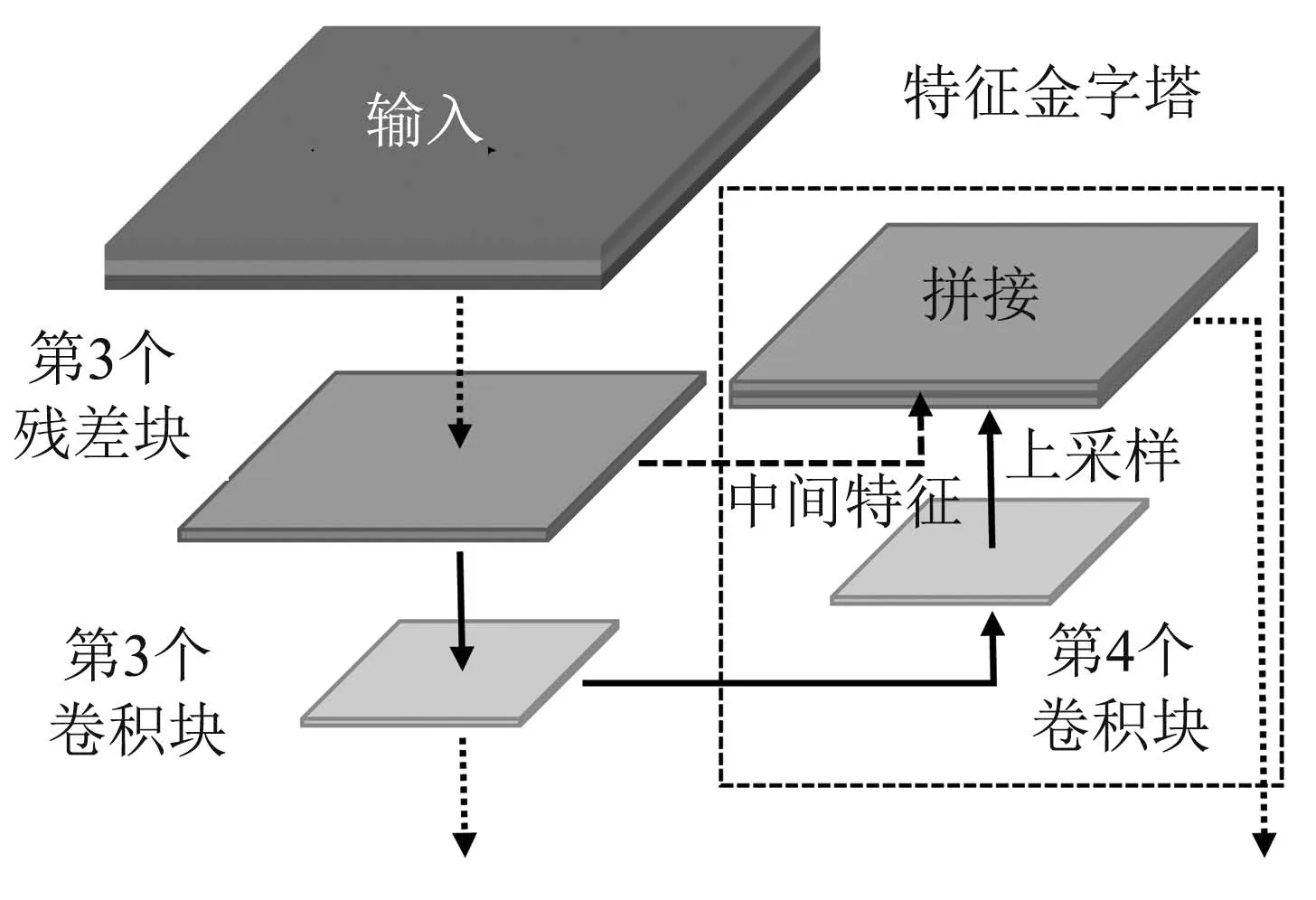
图3 小型特征金字塔的结构示意图Fig.3 Structure of a small feature pyramid

中间特征是骨干网络的第3个残差块中第4个卷积层的输出,与网络中第4个卷积块的输出经过上采样后的特征进行拼接.在图1可以看出,骨干网络只包含前3个CBL层,因此图3中进行拼接操作生成的输出代表了浅层网络特征和深层网络特征的融合.由于经过了多层卷积自上而下的特征提取,深层网络会保留绝大部分大目标的特征值,小目标的特征值被保存下来的很少甚至为零.因此采用特征金字塔结构提取多个不同层级网络的特征,通过上采样放大之后,将其自下而上的拼接在一起,实现了多个层级的特征融合,提高了网络对多种分别率下不同大小目标的识别能力.

之后将小型特征金字塔的两部分输出接入头部网络进行计算,生成两组包含不同感受野的图像,分别对自身包含的先验框进行调整,利用非极大值抑制的方法,针对原图中大小不同的目标进行识别与检测,提高神经网络对多尺度目标的整体检测能力.

2.2 数据增强方法

Mosaic方法是在切割混合[23]方法上进行拓展,生成的一个新的数据增强算法,不同于切割混合方法的两张图片覆盖融合,它是利用4张图片进行剪裁拼接,形成一张新的图片.这种方法可以更好地丰富目标物的背景,防止由于训练集背景相似而导致的网络泛化能力降低.

Yolov4–tiny算法的输出图像中包含有两种不同的感受野,而Yolov4算法的输出图像中则有3种不同的感受野,因此Yolov4–tiny算法对于多尺度目标的识别能力就会相对弱一些.所以,对数据增强方法进行改进,增强网络的泛化能力就显得尤为重要.

改进的马赛克数据增强方法如图4 所示.原始Mosaic方法是以图4中的上方与中间两条通道进行的特征增强,而改进Mosaic方法在原先的基础上增加了下方的通道,采用3条通道进行特征增强.第3条下方通道的输出,相较于上面两种,是对每行每列排列的图像数进行了增加而得到的.为了方便说明,将以3×3的规格新生成九合一的图片称之为m9,将以2×2的规格生成的四合一图片称之为m4,将不经过合并以1×1规格生成的图片称之为m1,m1,m4 和m9的比例为o:p:q.这样的组合方式,一定程度上使得训练数据集的尺度变化特性更加多样,从而进一步丰富了数据集,增加了背景的复杂程度.因此,网络可以在复杂背景的干扰下,更专注于对目标物特征的提取,增强了网络的鲁棒性.

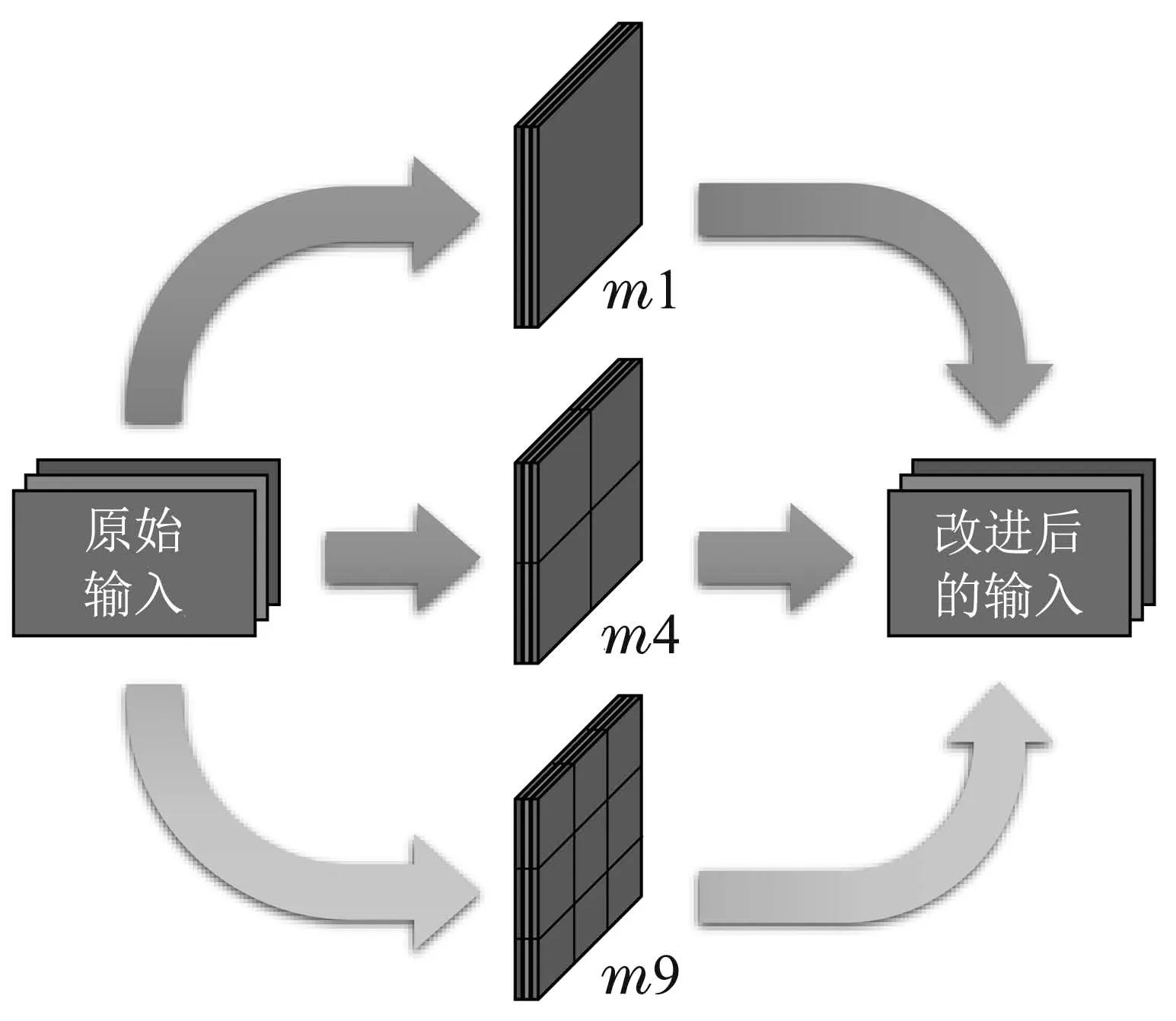
图4 改进的马赛克数据增强方法Fig.4 The improved Mosaic data enhancement method

九合一图像m9的生成方式如图5所示,主要分为A,B,C三个阶段.在A阶段,以输入图像的宽和高(W,H)作为边界值,首先对图像进行缩放,X轴和Y轴的缩放倍率为tX和tY,如式(3)–(4)所示:

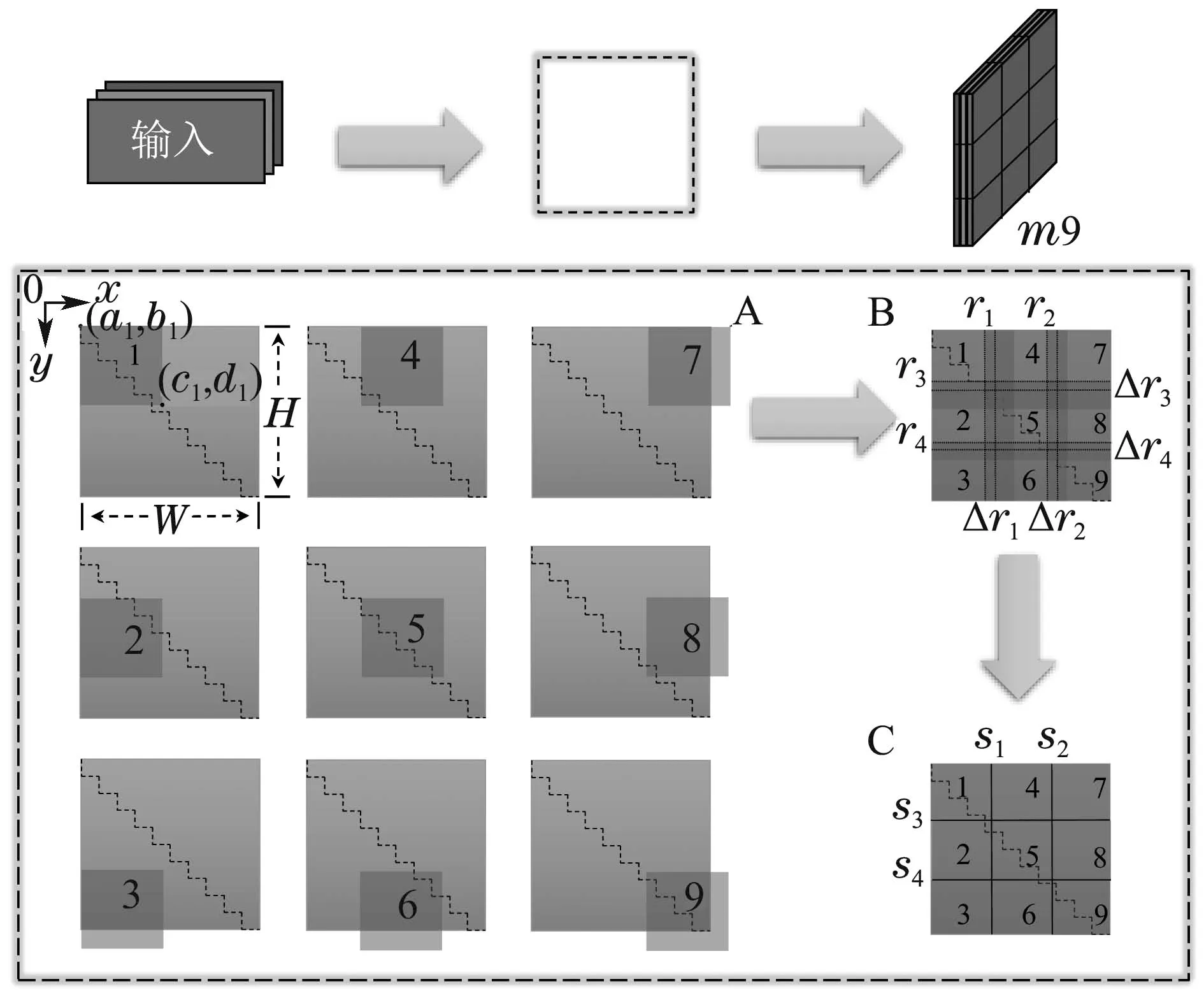
图5 m9图像的生成流程图Fig.5 Flowchart of m9 image generation

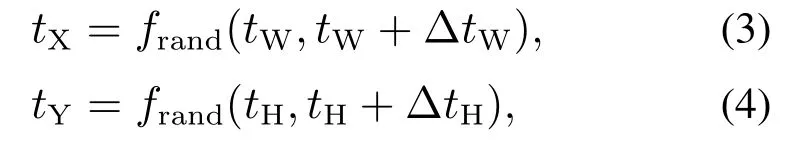
其中:tW和tH分别为宽和高缩放倍率的最小值,∆tW和∆tH分别为宽和高缩放倍率随机区间的长度,均为超参数.frand()表示随机值函数.

图像缩放后的左上角和右下角的坐标为[(ai,bi),(ci,di)],由式(5)到式(8)可得

二次电缆出线的护套采用直线布置，如图2(a)所示，且二次端子盒在电缆出口处未采取封堵措施，如图2(b),导致雨水沿二次电缆护套进入二次接线盒，接线盒内的CT端子引出处也未采取封堵措施，如图2(c)，导致雨水从接线盒进入CT箱体内部。

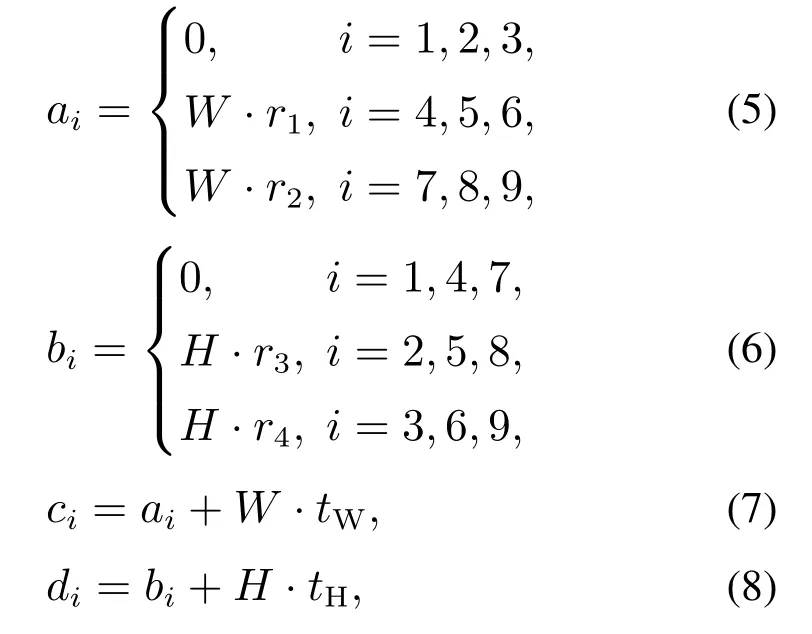
其中:r1和r2分别为X轴的除0点以外的两组图像左上角坐标点与0点的距离占总宽度的比值,r3和r4分别为Y轴的除0点以外的两组图像左上角坐标点与0点的距离占总高度的比值,同样也均为超参数.而灰色区域中的黑色短划线为比例尺,每一小段代表宽或高的十分之一,利用比例尺可以看出,第2张至第9张的图像和第1张的缩放比例一致,宽和高都是原来的tW和tH倍.

在B阶段,需要将上一阶段裁剪好的9张图片进行拼接,并裁减掉溢出边界框的部分,可以看到合并后的图像存在一定程度的重叠,因此需要对每个小区域进行划分.从A阶段的示意图中可知,当缩放后的图片按照坐标在指定位置进行放置时,会存在溢出边框的情况.此时需对溢出的部分进行裁剪,如式(9)–(10)所示:

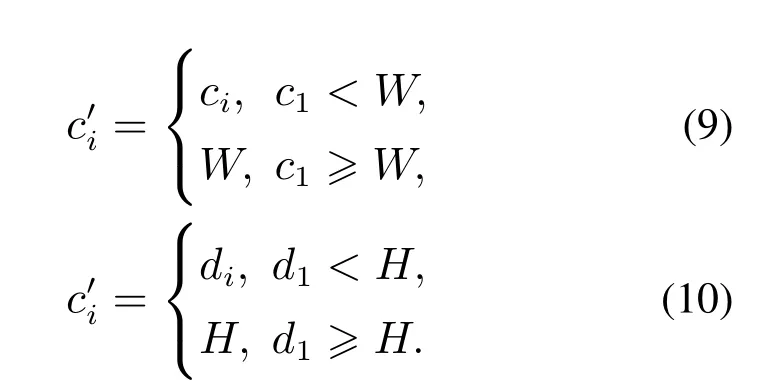
在边缘裁剪之后,利用8条两两平行的圆点线围成的4个方形区域,将其作为分割线的随机区间.其中,ri=(r1,r2,r3,r4)的值等于分割线坐标与0点的距离占边界长度的比值,∆i为分割线随机区间的长度.

在C阶段,将对内部重叠部分进行第2次裁剪,其分割线坐标si可由式(11)得

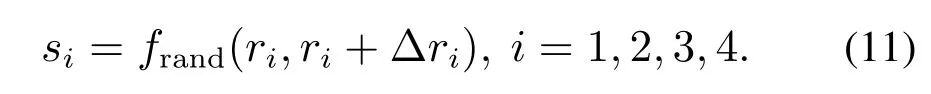
经过裁剪以后,得到了拼接完成的m9图像.由于原图在缩放拼接过程中存在部分缺失,对于处在原图边缘的目标有可能在操作过程中被截取部分或者完全截掉,因此,同样需要对这些目标对应的真实框进行裁剪甚至剔除,以满足目标检测的需要.

生成m4图像的方法与生成m9类似,如图6所示.左上角坐标()与分割线坐标由式(12)–(14)所示:

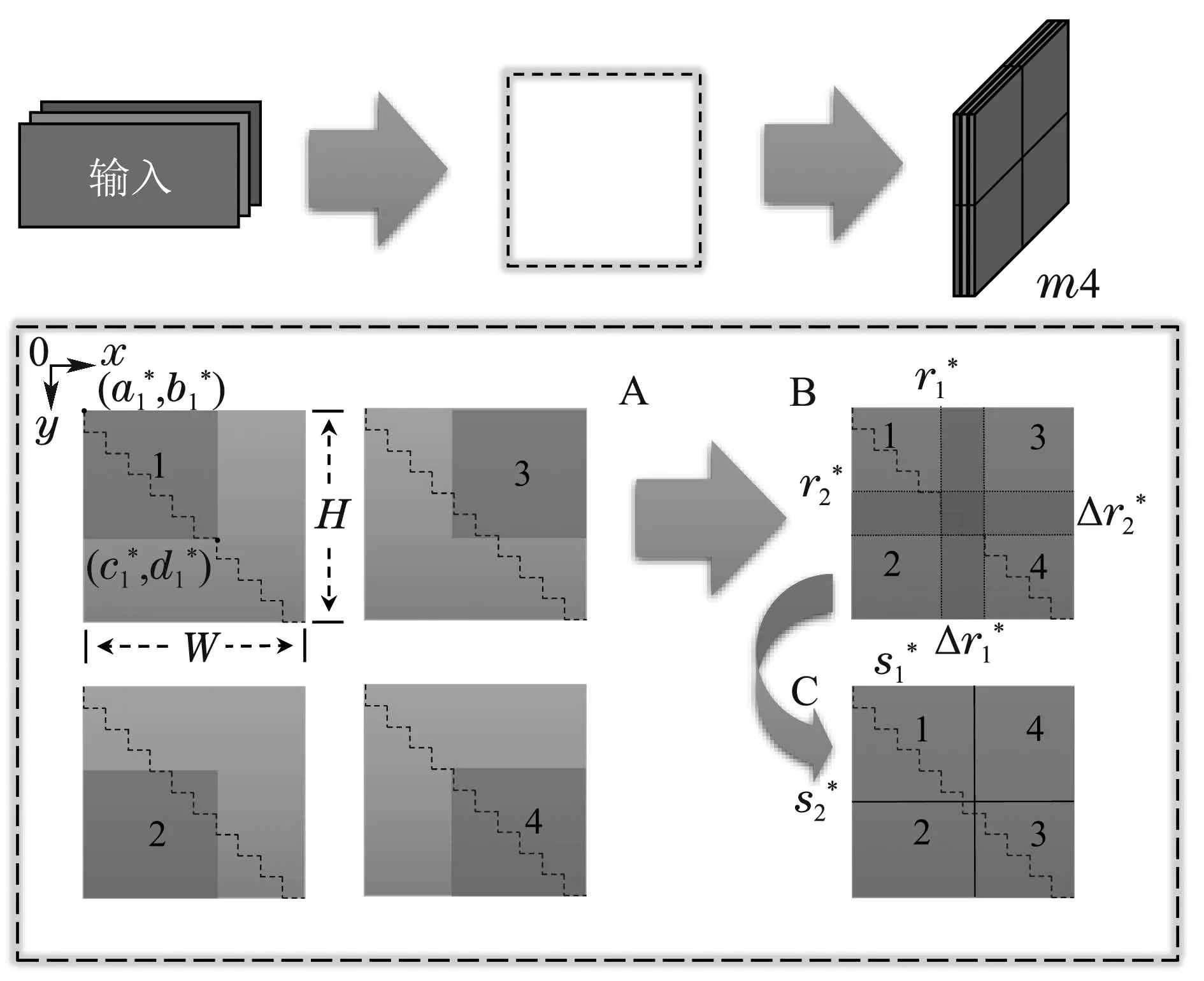
图6 m4图像的生成流程图Fig.6 Flowchart of m4 image generation

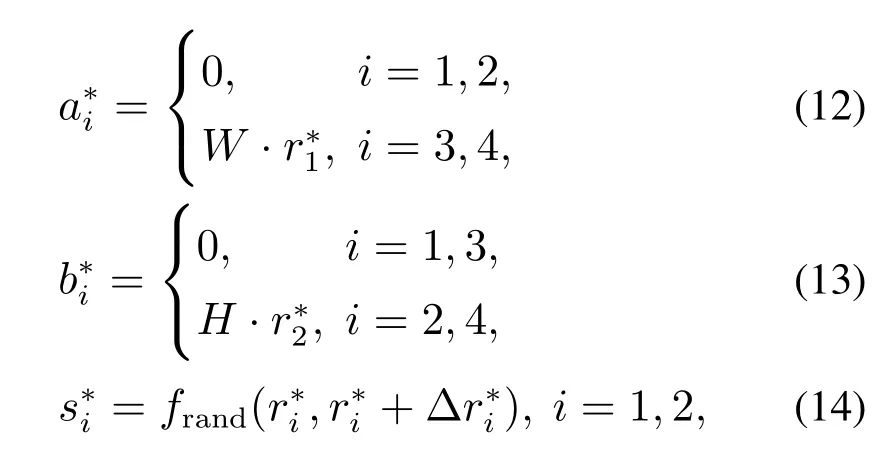
其中以∗作为m4图像与m9图像的区别符号.缩放倍率和及右下角坐标与m9 图像的计算方式一致,由于没有出现边框外溢出,所以只需要对内部重合部分进行分割裁剪.

m1图像由于不存在多张图片拼接的情况,因此进入网络之前只需要通过翻转、色域变化等常规方法进行特征增强.

2.3 网络优化方法

为了更好地结合船舶数据集的特点,Yolov4–tiny算法在开始训练之前,先利用K均值聚类算法将训练集内大小不一的真实框分成m类,这样得到的锚框更适用于检测船舶目标.在本文中m=6,这些锚框将根据大小被分成2组,每组3个框,去检测不同尺度的目标物体.此外,在训练开始前,先将网络模型在大型数据集中做训练,当其具备提取基础特征及抽象特征的能力时,再利用迁移学习方法进行微调,将训练完的权重和偏差作为初始值迁移至新的任务中进行训练.

3 实验仿真及测试

3.1 数据集规划

目前广泛使用的数据集,如:VOC 数据集[25]、COCO数据集[26]等包含的船舶只被分为了1类,存在图片尺寸随机且分辨率较低(不超过640×360)的特点.相比之下,本文中用于训练及测试的船舶数据集[27]一共包含7000 张图片,其分辨率为1920×1080,它们截取自监控摄像机所拍摄的视频片段,而这些摄像机是属于沿海岸线部署的海面监控系统,其包括50个不同位置的156个摄像机.数据集中包含6种不同类型的船舶,其数目与类别如表1所示.

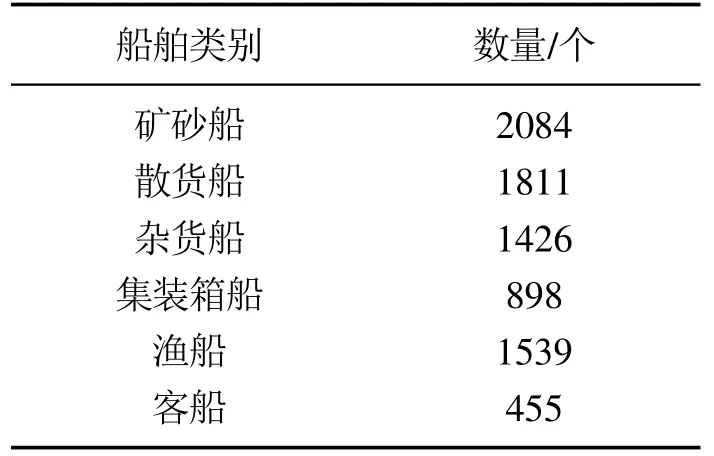
表1 船舶数据集目标物类别与数量Table 1 Ship data set target object category and number

这些图像中的船舶拥有不同的光照条件、观测角度、远近尺度以及重叠程度,使数据集的复杂程度大大提升,增加了目标检测算法识别的难度.

3.2 训练与测试结果

本文的算法是在开源的神经网络框架Pytorch(3.8.5)上进行实现的.计算工作站配置包含1个GPU(GeForce RTX 3090),CPU (AMD Ryzen 9 3950x 16 Core/3.5 GHz/72 M),以及128 G RAM.小型移动测试平台是基于NVIDIA Jetson Xavier NX开发板进行搭建,由1个1080p摄像头模组,供电模组,显示输出模组及控制模组组成.

在训练开始之前,先将数据集进行分类.选择6000张几乎无遮挡的船舶目标图片作为训练集,1000张发生不同严重程度重叠的船舶图片作为测试集.通过对目标识别算法的优化,使目标船舶在发生不同程度的重叠与遮挡时,能够更加快速且准确地捕捉到目标,减少提高识别准确率.实验中Mosaic方法的参数如表2所示,网络优化方法中的参数如表3所示.

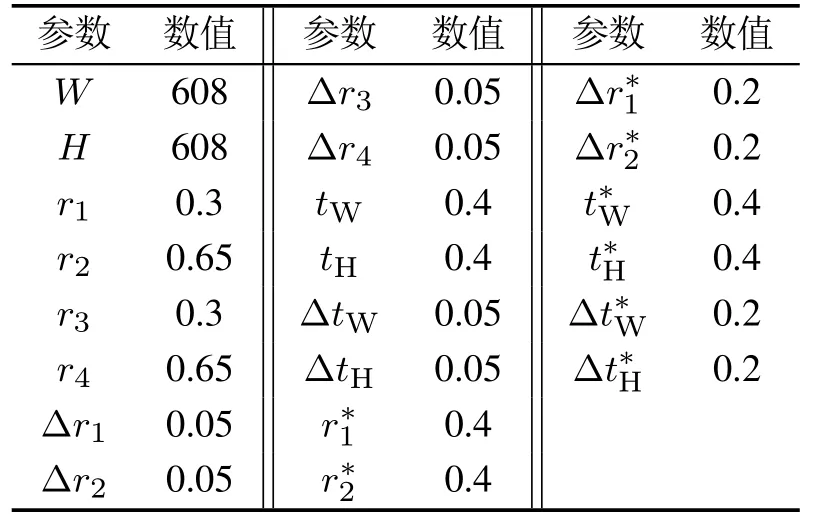
表2 马赛克数据增强方法中的实验参数Table 2 Experimental parameters in Mosaic data enhancement methods

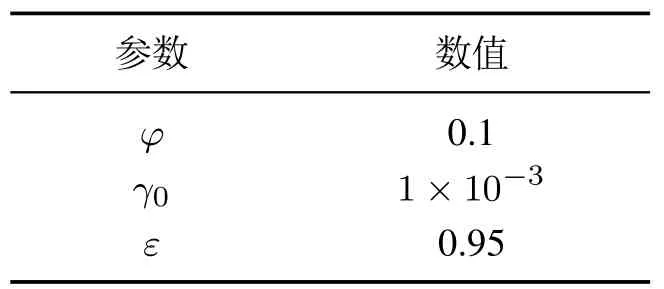
表3 网络优化方法中的参数Table 3 Parameters in network optimization methods

训练数据集中用于训练和验证的图片以9比1的比例随机分割,训练开始后,网络经过100次迭代后停止,图7表示Yolov4–tiny算法在不同迭代次数下的识别准确率,图中图例的数值为o:p:q的值,准确率的高低由各类别平均精度的平均值(mean average precision,mAP)来表示.

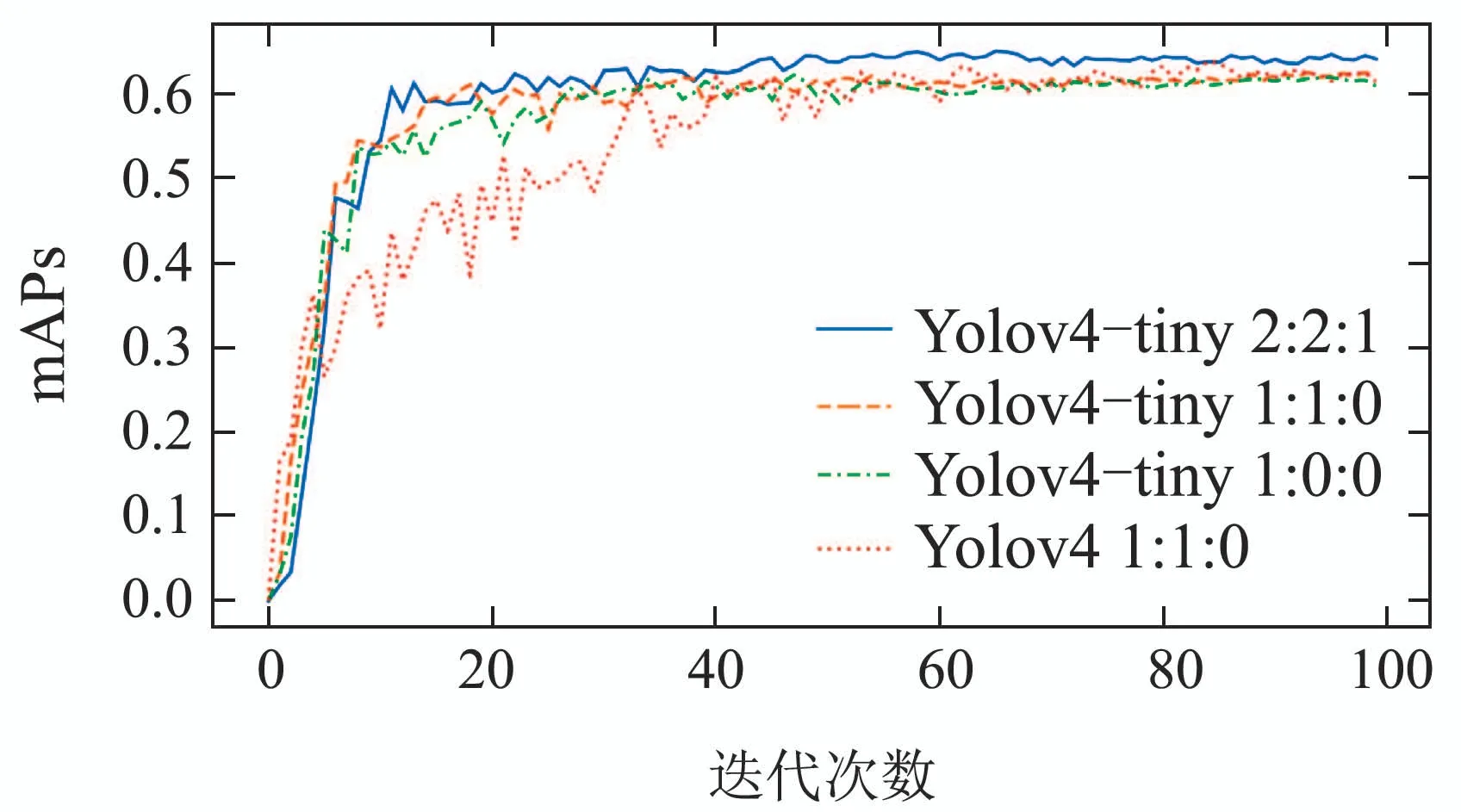
图7 Yolov4–tiny算法在不同迭代次数下的识别准确率Fig.7 mAPs of Yolov4–tiny algorithm with different number of iterations

从图7中可以看出,在趋向于平稳的后二十次迭代过程中,黄色曲线的值略高于绿色曲线的值,使用Mosaic方法之后Yolov4–tiny算法的识别结果略有提升,而蓝色曲线表示的改进Mosaic方法则大大提高了识别准确率,甚至高于使用原始Mosaic方法的Yolov4算法的识别准确率.所以改进Mosaic方法不仅提高了Yolov4–tiny算法的识别准确率,相对于Yolov4算法大大提高了船舶识别的检测速度.运用m4和m9方法的数据增强实验过程如图8所示.

图8 m4与m9方法的实验过程示意图Fig.8 Experimental procedure of m4 and m9 methods

图7中识别准确率最高的曲线是使用改进Mosaic方法进行训练的,其使用m1,m4和m9方法作为输入的概率按照比例o:p:q=2:2:1来进行.为了探究比例的不同对识别准确率的影响,本文进行了多组实验比较,结果如表4所示.同时,将改进Mosaic方法与3种同类代表性数据增强方法进行了比较,结果如表5所示.

从表4的前5行的对比可以看出,如果训练集中的所有图像都使用m4或m9方法进行数据增强,而抛弃原始图像的话,相较于不使用数据增强方法的情况,其识别准确率反而会降低,而无论是m4或m9方法,结合50%的原始图像同时训练,其准确率都会提升.因此,即使使用数据增强方法,也不可以丢弃原始图像,这一点同时也可以通过表5中的前8行数据来印证.

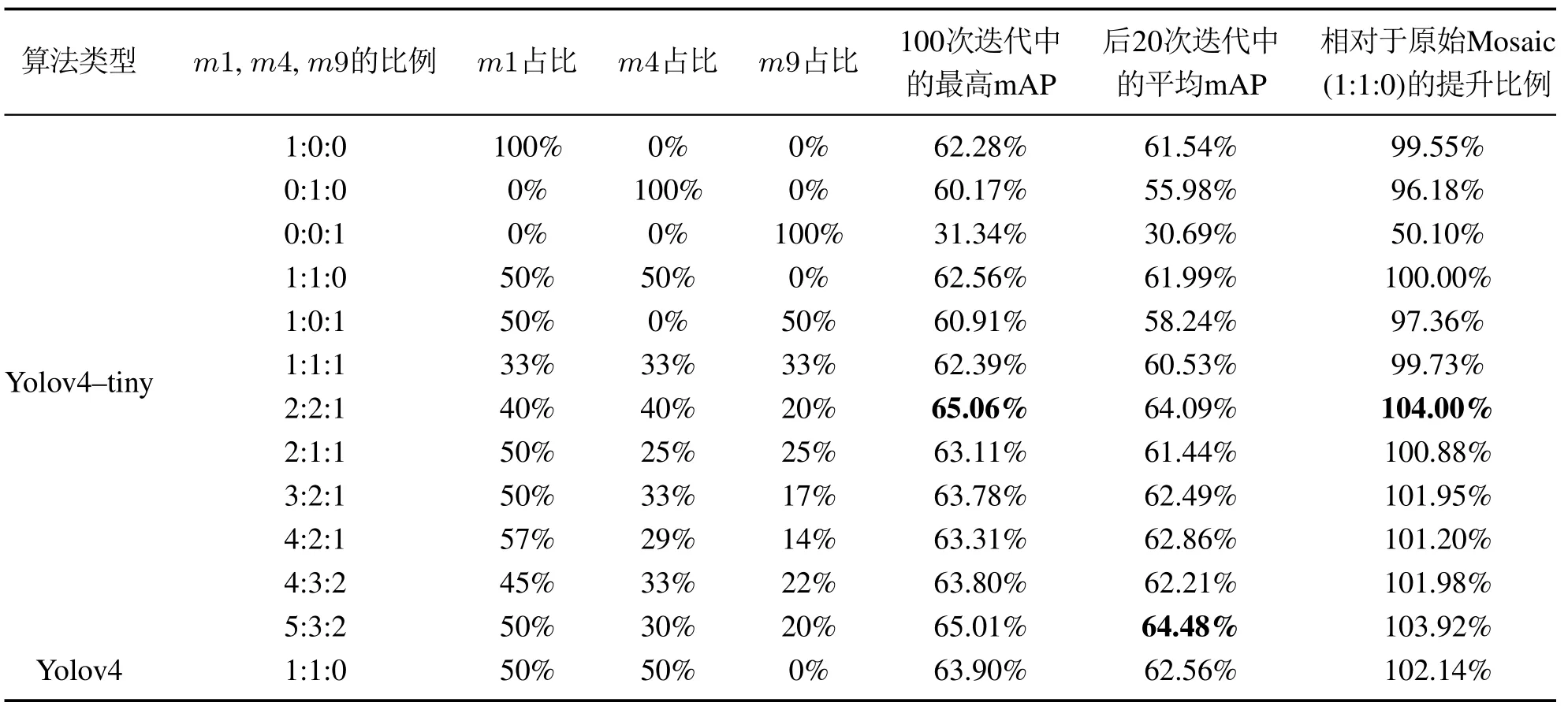
表4 不同比例下Mosaic数据增强方法对目标识别准确率的影响Table 4 Effect of Mosaic data enhancement methods on target recognition accuracy at different scales

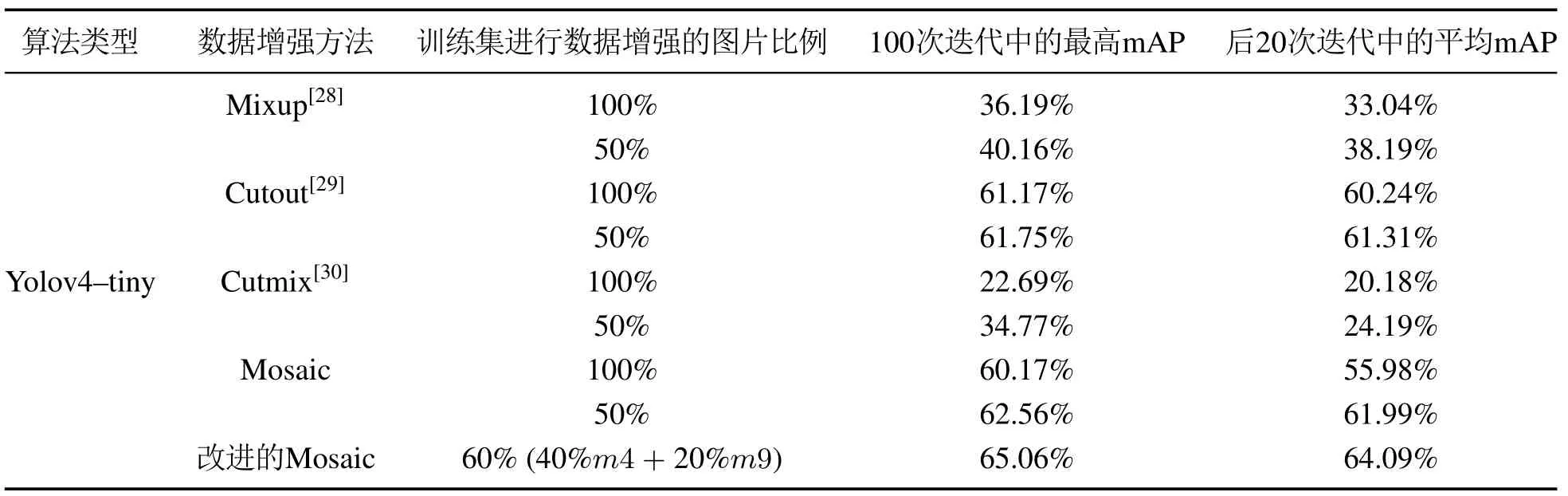
表5 不同数据增强方法的目标识别准确率Table 5 Accuracy of target recognition with different data enhancement methods

而同比例使用m1,m4及m9三种方法进行训练时(当o:p:q=1:1:1时),其准确率较原始Mosaic方法(当o:p:q=1:1:0时)几乎一致,并没有得到预期的提升,考虑到可能是因为按照此方法训练时原始图片的比例过小(仅有30%),所以在表4的第7至12行进行了多种比例的实验,并且将m1的占比调至40%以上,准确率较原始Mosaic方法都有了不同程度的提升,这说明数据集应当以m1数据作为重点,让网络学习好目标的整体特征,在此基础上利用m4与m9分别对局部特征进行加强学习,提高网络的泛化能力.并且可以发现,当m4与m9的占比只差在10%∼20%且m1的占比在40%∼50%时,网络的训练效果会更好,即当o:p:q=2:2:1和o:p:q=5:3:2时,mAP的最高值相对原始Mosaic方法提升了2.5%,并且高于使用原始Mosaic方法训练的Yolov4算法.

为了进一步测试网络对重叠目标的识别能力,利用小型移动测试平台对海面进行实时检测,测试地点位于鼓浪屿(中国,厦门).以一段在行进过程中发生重叠的两艘渔船的实时视频片段作为实验内容,计算网络在各个时刻的识别能力,视频片段分辨率为1080P,时长38 s,每秒24帧,共912帧,测试结果如图9所示.实测实验中选用的权重文件为100次迭代中最高mAP所对应的权重.

在图9中可以看出,第691帧两艘船已经发生严重重叠时,使用改进Mosaic方法的Yolov4–tiny算法依然可以将两艘船同时识别出来,而使用原始Mosaic方法和未使用Mosaic方法的Yolov4–tiny 算法只能识别其中的一艘船.在第756帧两艘船正在摆脱重叠的过程中,使用改进Mosaic方法和原始Mosaic方法的Yolov4–tiny算法已经可以将两艘船同时识别出来,而未使用Mosaic方法的Yolov4–tiny算法依然只能识别其中的一艘船.这进一步说明了改进Mosaic方法对提升重叠目标检测能力的有效性.

图9 重叠检测实验对比图Fig.9 Overlap detection experiment comparison chart

与此同时,为了探究网络对于目标物特征识别能力的影响,其梯度加权类激活映射图(Grad-CAM)[30]如图10所示.

在图10中,通过对比在不同训练方式下的梯度加权类激活映射图,可以直观地观察到网络对于测试图片感兴趣区域的不同.第一,对于发生重叠且不完整的船舶大目标,当o:p:q=2:2:1时,此时网络所关注的中心点有3个,其中两个位于船舶上层建筑的位置,可以更好地对船舶的个数进行判断,而且重点关注了图片的上半区域,相比于其他两种情况,对下半区域的背景特征有了更好的抗干扰能力.另外,相较于未使用Mosaic方法训练的情况,原始Mosaic方法的确增强了网络对于船舶的关注度.第二,对于发生重叠且完整的船舶小目标,当o:p:q=2:2:1时,网络对于不同船舶位置的关注点较为准确且边界感较强,同样可以增加对船舶个数的判断能力,而未使用Mosaic方法训练下的网络,对于小目标的识别能力明显更弱.因此,对于不同尺度的船舶目标,改进的Mosaic方法在一定程度上可以提高网络的识别能力.

图10 不同训练方式下梯度加权类激活映射图的对比Fig.10 Comparison of gradient-weighted class activation mapping maps under different training methods

由于小型移动设备的算力有限,在1080p分辨率下识别速度较慢,因此对不同分辨率视频中的船舶目标进行检测测试,网络的识别速度由表6所示.

由表6可以看出,由于Yolov4网络结构较复杂,权重参数较多,导致其识别时需要的算力较高,因此在4种分辨率下的识别速度都很低,而Yolov4–tiny算法网络结构较简单,权重参数较少,识别时需要的算力较低.Yolov4–tiny算法在360p视频分辨率下的识别速度为其在1080p视频分辨率下的179.50%,为Yolov4算法在360p视频分辨率下的识别速度的462.60%.

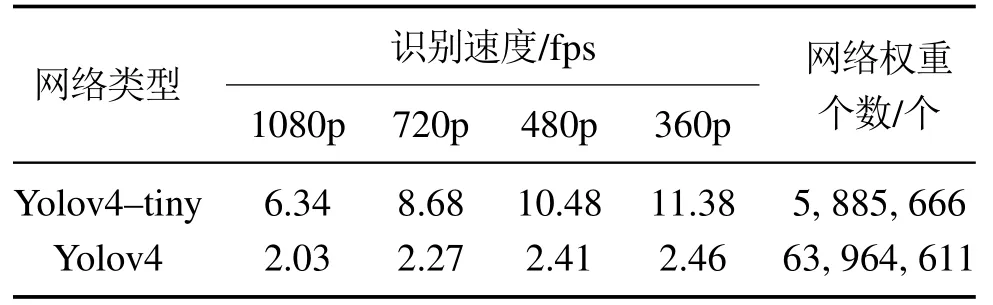
表6 不同分辨率下的识别速度对比Table 6 Comparison of recognition speed at different resolutions

由于不同分辨率下不同算法的识别速度不同,因此改进Mosaic在不同分辨率下的识别能力的重要性便不言而喻.于是,通过对比在重叠开始至重叠结束的区间内,以应用不同Mosaic方法的Yolov4–tiny算法将两艘船正确识别并分离的帧个数,判断其对于重叠问题的识别能力,具体实验结果如表7所示.

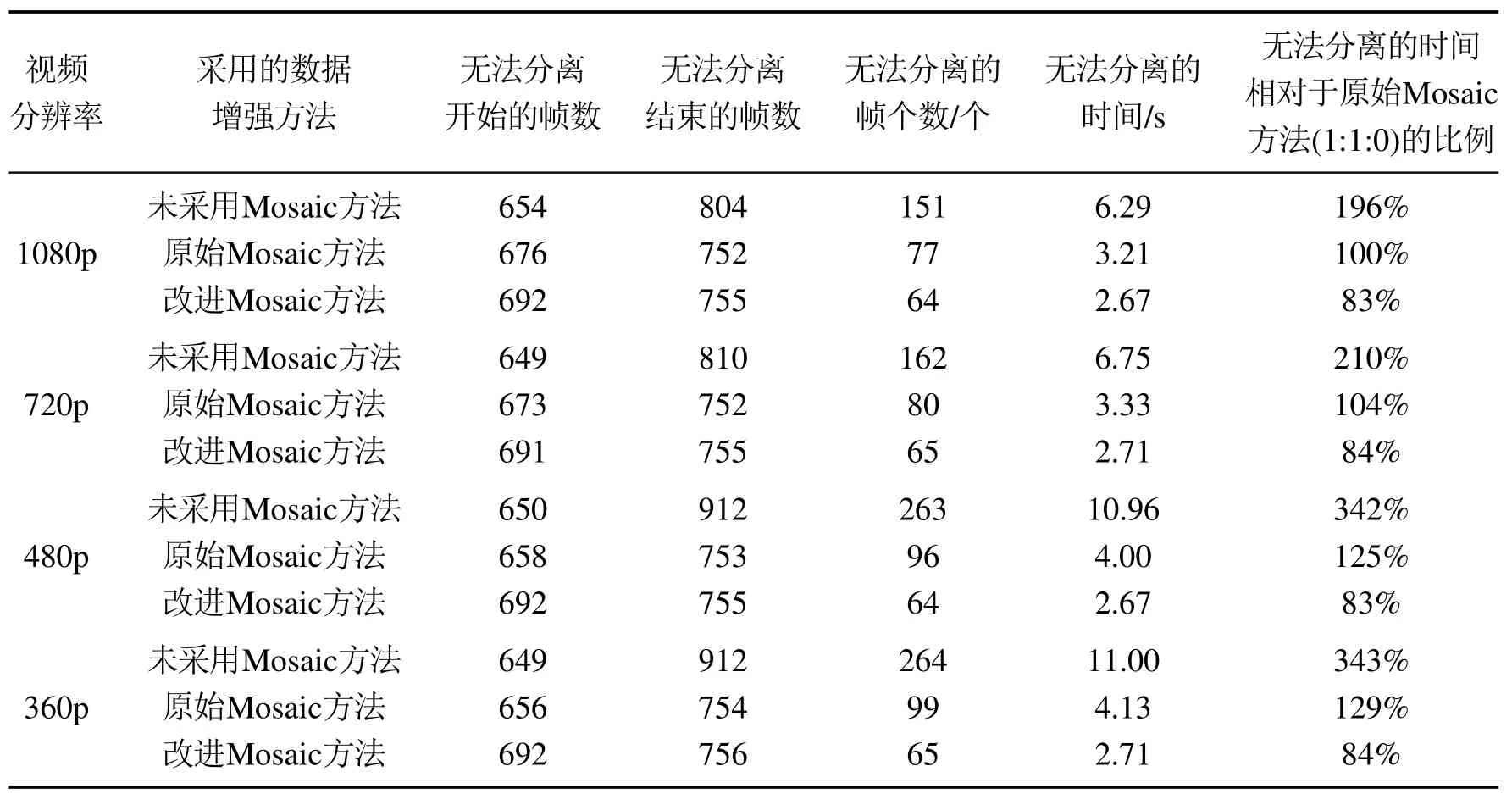
表7 采用不同Mosaic方法在不同分辨率下的对于重叠问题的识别能力对比Table 7 Comparison of the recognition ability of overlapping problems at different resolutions using different Mosaic methods

从表7中可以看出,随着分辨率的下降,各个算法对于重叠目标识别速度都有不同程度的减弱,其减弱的程度可以由无法分离的时间增长率来表示,如图11所示.由此可见,使用改进Mosaic方法的Yolov4–tiny算法在4种不同的分辨率下都取得较大了优势,不仅在船舶目标产生重叠时,无法分离重叠目标的时间较短,而且在分辨率发生下降时也可以维持高识别率.

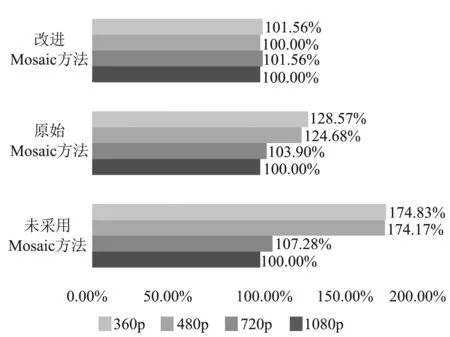
图11 采用不同Mosaic方法在不同分辨率下无法分离的时间增长率Fig.11 Time growth rates that cannot be separated at different resolutions using different Mosaic methods

实验证明,改进Mosaic数据增强方法对船舶重叠目标的识别效果有一定的提升,应用于Yolov4–tiny算法可以部署于小型移动设备,可以灵活地装配在各类平台上,从而实现在离线状态下对海面船舶目标的实时监测.

4 结论

本文以Yolov4–tiny算法为实验基础,提出了一种改进的马赛克数据增强方法,并对马赛克填充的不同比例进行了对比试验,探究其对船舶重叠目标检测准确率的影响.在仿真实验中,对船舶数据集进行分析,以数据集中的船舶重叠目标作为检测对象,相对于原始算法,改进后的方法在测试数据集的识别准确率上提高了2.5%,达到了与原始Yolov4算法同样的检测效果,提升准确率的同时降低了算力的消耗.在实测实验中,将算法部署在小型移动测试平台上进行实测,相对于原始算法,改进后方法的目标丢失时间减少了17%,在不同视频分辨率下的识别稳定性上提高了27.01%.因此,目标识别算法经过改进的马赛克数据增强方法训练后,可以提升其对船舶重叠目标的识别能力.