一类时变系统中补偿器的功能和设计

开平安,曾世权,邓 慧

(1.国家发展和改革委员会能源研究所,北京 100055;2.暨南大学能源电力研究中心,广东珠海 519070)

1 引言

由于功能完整、结构简单和参数易整定,PID控制器被广泛应用在实际过程控制中[1],特别是对于确定性时不变系统[2],有良好控制功能和控制品质.但对于时变过程对象,受限于其固定的控制参数和结构,PID控制器难以满足在对象在不同时间工况点下的品质要求[3–4],实现PID在非线性与不确定对象上的鲁棒性能增强[5–6],对拓展PID控制器应用范围,有重要意义,一般来说,有以下两类途径.

第1类途径是PID参数优化整定,如Grimholt等[7]利用基于梯度优化的有限差方法,来预估PID参数,Huang等[8]提出P系统变体算法对PID参数进行多目标优化,Martins[9]使用积分最小时间标准,设计PID参数优化算法,但以上方法一般需要建立对象模型或需在线获取过程参数(即所谓的“数据驱动”);第2类途径是控制器变结构,如Boiko[10]设计了一种根据状态向量值变化在多个PID之间切换的变结构控制器,用于时变水位被控对象,Bedwani等[11]提出了一类PI和PD变结构控制策略,用来满足非线性对象对响应速度和稳态误差的双重需求,Zhang等[12]组态了一种根据瞬态被控误差自动切换结构的PID控制器,用于大型望远镜的变速控制,以上变结构方法由于算法多样复杂,工程实现的难度要远大于常规PID控制器.

本文考虑控制工程的易实现,通过控制器简单变结构,针对标称工况工作点的多类优化指标,提出在基本PID上增加一个补偿器,使得在时变被控对象在变工况下控制系统的闭环输出与标称工况的输出相同,应用和仿真验证了本文提出的带补偿器PID能提高了时变系统鲁棒性能,改进控制系统整体品质指标.

2 具有强鲁棒性能的补偿器设计

图1是本文设计的带补偿器强鲁棒性能控制系统框图.

在图1中,PID(s)=kr(kp+ki/s+kds/(tds+1)),被控对象P是一个不确定或者非线性系统,r=Ur/(T0s+1)2,其中Ur是幅度为|Ur|的阶跃信号,闭环系统输出y跟踪期望的轨迹r.

定义1被控对象P是一个不确定或者非线性系统,由一些不同运行工况表达为传递函数Gi(s),构成(i=0,1,···,n),或者通过线性化非线性系统得到的传递函数Gi(s)构成(i=0,1,···,n).

定义2不失一般性,令Gi(s)∈P,

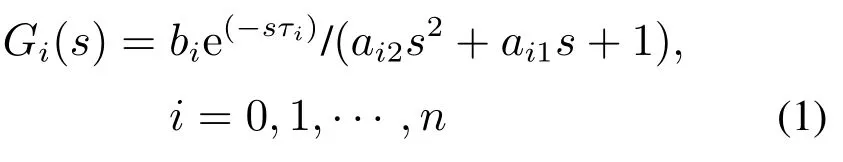
是稳定的.

定义3Gp(s)是标称运行工况下的传递函数,PID∗控制器的参数K∗=是基于标称运行工况Gp(s)经过某种优化指标设计的,PID∗的输出up=PID∗e(t),其中e(t)=r(t)−y(t),基于Gp(s)设计的优化PID∗闭环系统输出yp=Gp(s)up是稳定的,而且满足某种优化指标.

定义4优化指标[13–14]包括

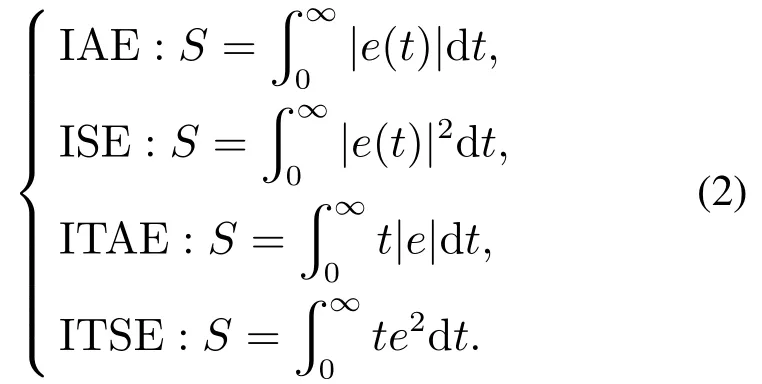
定理1如果基于标称运行工况Gp(s)经过优化指标设计的PID∗的输出up=PID∗e(t),其中e=r −y,闭环系统输出yp=Gp(s)up是稳定的并且满足控制系统的品质指标,设计的补偿器kf如图1所示,使得所有的闭环系统输出yi=yp,i=1,2,···,n,则补偿器kf=,其中Gi(s)∈P,i=1,2,···,n.

证根据定义3,yp=Gp(s)up,因为yi=Gi(s)upyp,考虑带补偿器kf的控制器,其输出为u=up+uq,使得所有的基于运行工况Gi(s)闭环系统输出yi=yp,i=1,2,···,n,从图1可知

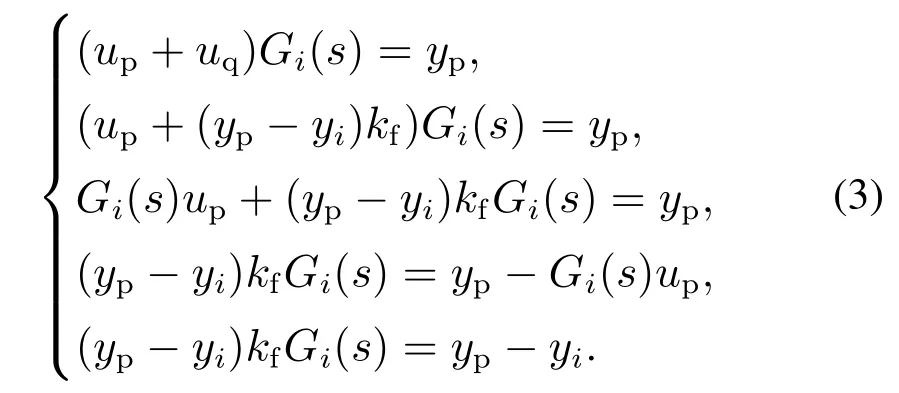
所以

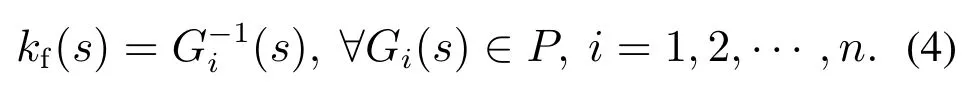
证毕.

3 工程应用

3.1 无延迟系统

考虑造纸厂张力控制对象的不确定模型,P在3种工况下的传递函数分别是

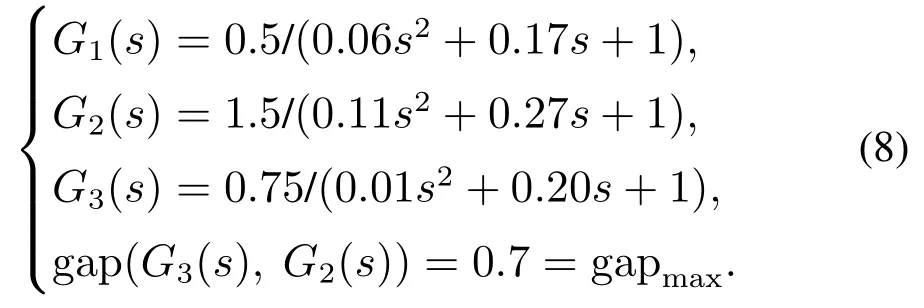
选择Gp(s)=G3(s),Gq(s)=G2(s),在图1所示控制器中,令控制周期ts=0.001 s,T0=0.04 s,经过规一化处理后,Ur为幅度为1 的阶跃信号,要求系统输出y在0.7 s内达到1.

基于标称工况Gp(s)设计优化的PID∗控制器参数

图2–4分别显示了有/无补偿器情况下,应用相同的优化PID∗控制器参数K∗,在单位阶跃信号Ut输入下,Gp(s),G1(s)和G2(s)闭环系统输出y和y1.

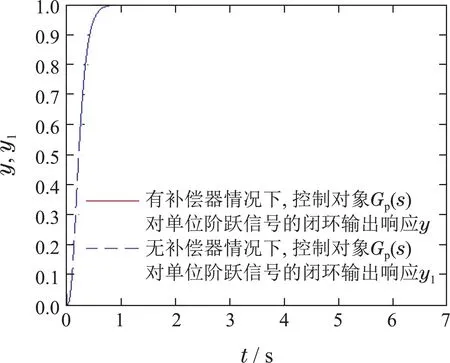
图2 有/无补偿器情况下Gp(s)闭环系统输出(2个曲线重合)Fig.2 The closed-loop system output of Gp(s)with and without compensator(the 2 curves coincide)

从图4可以看出,在无补偿器情况下,G2(s)的闭环系统输出是发散不稳定的,应用补偿器后,系统稳定,满足控制系统的性能指标.这说明应用补偿器后,能够使得系统整体达到稳定.

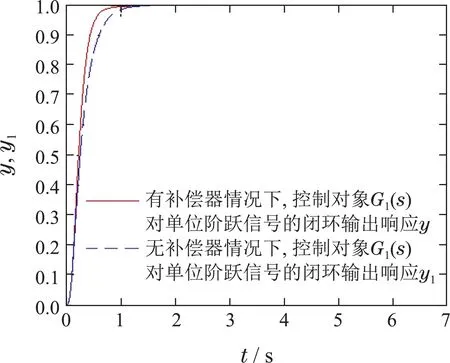
图3 有/无补偿器情况下G1(s)闭环系统输出Fig.3 The closed-loop system output of G1(s)with and without compensator

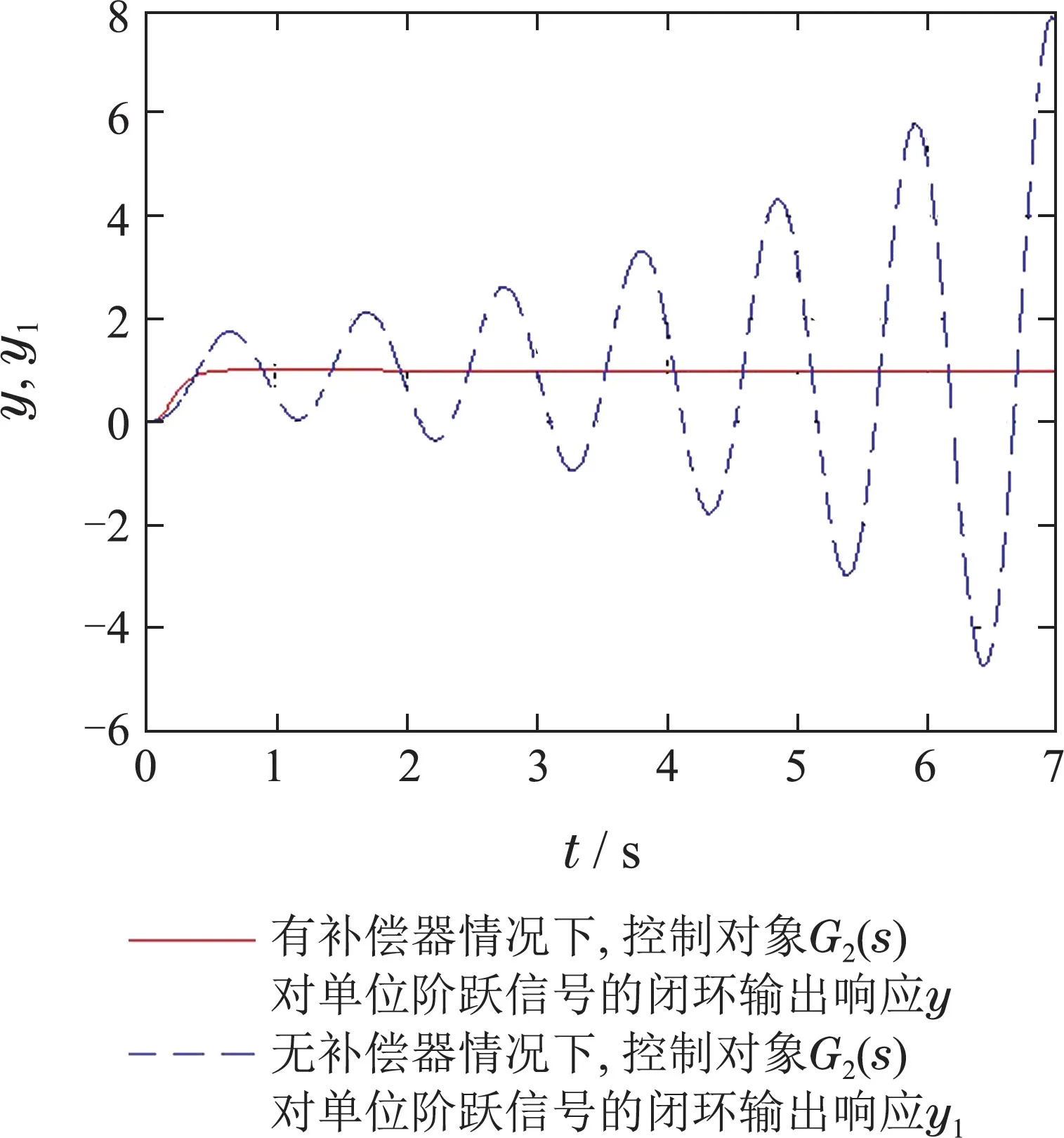
图4 有/无补偿器情况下G2(s)闭环系统输出Fig.4 The closed-loop system output of G2(s)with and without compensator

3.2 有纯延迟系统

考虑某发电厂热工控制对象不确定模型,P在3种工况下传递函数分别是

选择Gp(s)=G3(s),Gq(s)=G2(s),图1所示控制器中,令控制周期ts=0.2 s,T0=7 s,经过规一化处理后,Ur为幅度为1的阶跃信号,要求系统输出y在190 s内达到幅值1.

基于标称工况Gp(s)设计优化的PID∗控制器参数

图5–7分别显示了有/无补偿器情况下,应用相同的优化PID∗控制器参数K∗,在单位阶跃信号Ur输入下,Gp(s),G1(s)和G2(s)闭环系统输出y和y1.

图5 有/无补偿器情况下Gp(s)闭环系统输出(2个曲线重合)Fig.5 The closed-loop system output of Gp(s)with and without compensator(the 2 curves coincide)

从图6看出,有补偿器时,G1(s)工况下的闭环输出达到稳态时间比无补偿器时要快.从图7看出,有补偿器时,G2(s)工况下的闭环输出比无补偿器时超调量要小,达到稳态时间要快.在2种工况下,有补偿器比无补偿器,系统的控制品质都得到改善,鲁棒性能得到提高.

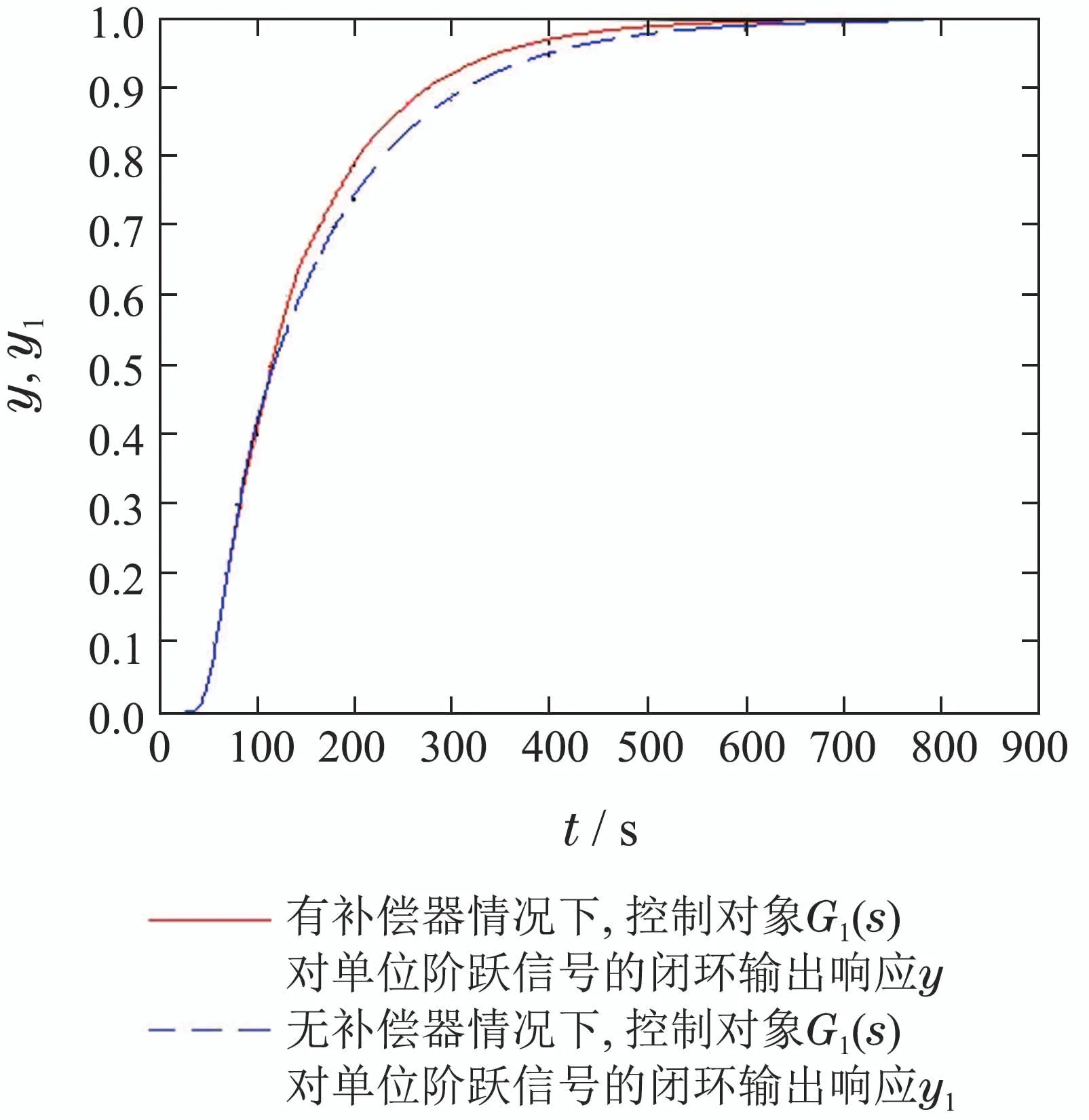
图6 有/无补偿器情况下G1(s)闭环系统输出Fig.6 The closed-loop system output of G1(s)with and without compensator

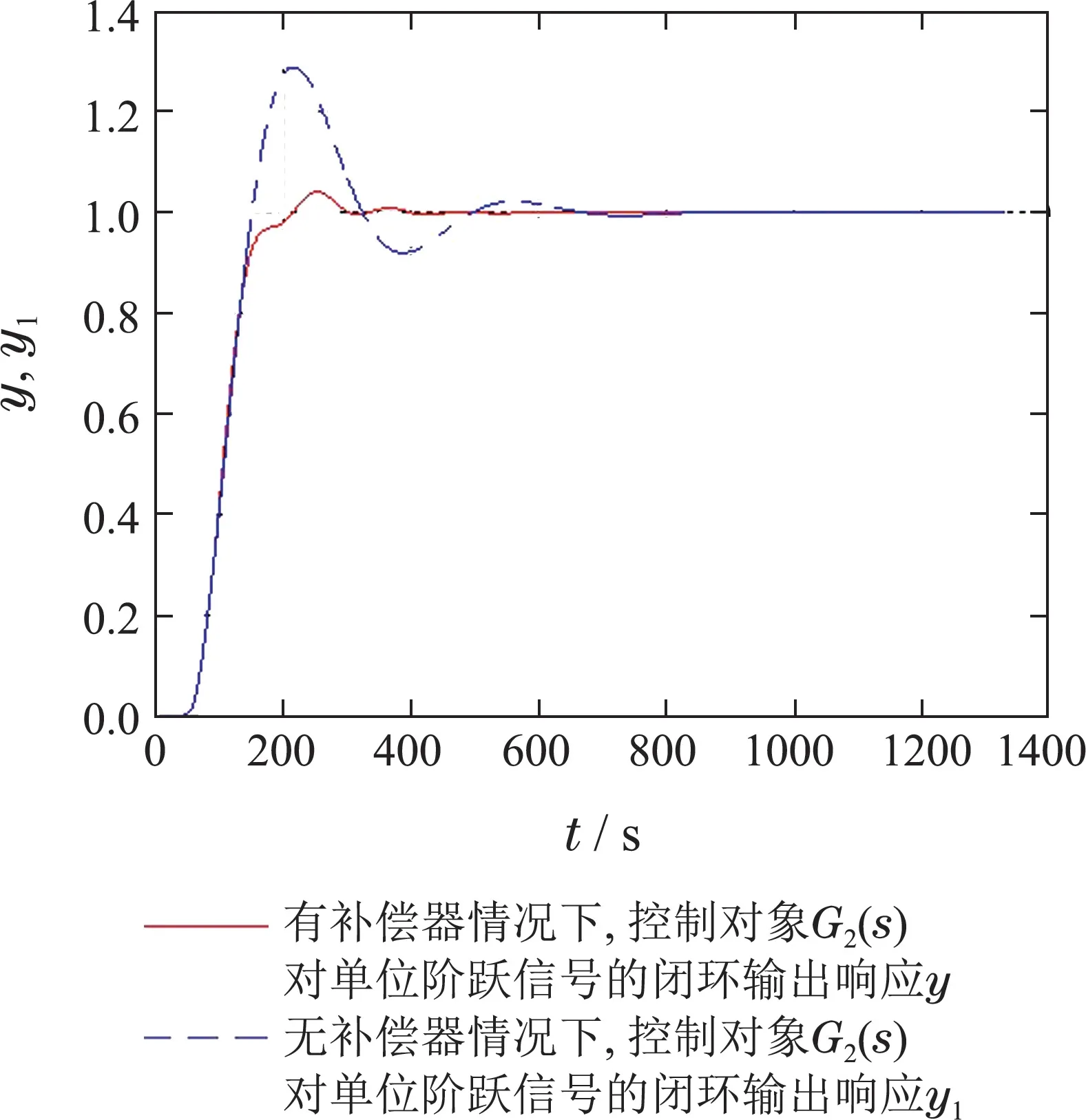
图7 有/无补偿器情况下G2(s)闭环系统输出Fig.7 The closed-loop system output of G2(s)with and without compensator

4 结论

为提高时变系统的鲁棒性能,改善控制系统的品质指标,本文基于标称工况工作点在某一优化指标下设计PID控制器,为了使其他工况下系统的闭环输出与标称工况下的输出相同,本文设计了具有严格的真分式正则传递函数补偿器,工程仿真验证了本文设计的补偿器能有效提高时变系统鲁棒性能,改善了控制系统的品质指标.