非平衡有向网络的完全分布式凸优化

时侠圣 林志赟 王雪松 董世建

(1.中国矿业大学地下空间智能控制教育部工程研究中心,江苏徐州 221116;2.中国矿业大学信息与控制工程学院,江苏徐州 221116;3.南方科技大学电子与电气工程系,广东深圳 518055)

1 引言

5G通信在4G通信的基础上拥有更高的带宽和更快的数据传输速率,随着5G通信的出现以及大规模应用,5G通信技术的发展进一步推动了物联网、自动驾驶汽车和智能设备等新兴技术的发展和普及.在这些应用中,如何从各个分布式设备收集的数据中学习隐藏的参数是很有意义的事[1].这其中有一类问题可以定义为分类、回归或风险最小,其核心是一个简单的成本和优化问题.庞大的数据和隐私问题限制了数据共享,因此,局部和分布式优化问题得到了广泛的关注[2].而分布式多智能体技术的发展也促进了该问题的研究与发展.在基于多智能体系统的分布式优化问题中,各智能体协同最小化局部成本函数和.这类优化问题在很多应用中得到关注[3–5],比如分布式学习[6]、源定位[7]和编队控制[8]等.

近年来,许多分布式优化算法被设计出来.包括连续时间算法[9–14]和离散时间算法[15–16].连续时间算法要求所依赖智能体可连续执行微分方程,例如机器人等.而离散时间算法则是一种迭代策略,更适应于计算机芯片等运行主体智能体,应用较为广泛.后续本文以离散迭代策略为目标,阐述该领域最新研究成果.分布式优化领域中最早的设计方法都是基于梯度下降[17].该算法也被广泛推广到受约束分布式优化问题[18].该类算法计算简单且直观,但是衰减步长容易导致算法收敛速度降低.此外,基于拉格朗日对偶法的分布式凸优化算法也得到了研究,进而引出了分布式对偶分解算法[19]和分布式交替乘子算法[20].相比于衰减步长梯度下降法,该类算法虽然计算较复杂,但收敛速度更快,且可实现线性收敛.为了同时实现算法的计算简单和快速收敛,许多快速算法被提出,比如分布式Nesterov加速算法[21–22]和分布式一阶精确算法[23].其中文献[22–23]通过梯度跟踪技术实现算法的固定步长控制.

注意到上述算法都是建立在无向网络基础上,即若系统中智能体i能够发送信息给智能体j,那么智能体j也能发送信息给智能体i.如文献[24]所述,上述算法的实现都需要构建一系列双随机矩阵.然而在一些实际应用中,此类通信机制是无法满足的.例如拥有不同能量等级的智能体其通信能力是有区别的,进而导致信息的单向传播.在有向网络中,双随机矩阵的特性(简称为平衡有向网络)一般难以满足,因此接下来本文主要分析非平衡有向网络下的研究成果并做进一步的算法改进.为了解决有向网络下的分布式优化问题,有部分学者将Push-sum(推和)方法引入进来,提出了一类分布式优化算法[25–26],该方法的基本思想是通过动态跟踪伴随矩阵1特征根所对应的特征向量,并利用此向量调整单向通信网络的不平衡性,引导算法收敛到凸优化问题的最优解.其中伴随矩阵只需确保列随机或者行随机.后续很多学者基于此提出了加速算法[27–30],其中文献[27]要求伴随矩阵行随机、文献[28]要求伴随矩阵列随机,而文献[29–30]则分别是在文献[27]的基础上增加类Nesterov和重力球与Nesterov双动量项进一步提高算法收敛速度.另一类算法则是通过同时构造一个列随机矩阵和一个行随机矩阵[31–33],其中行随机矩阵确保了算法的一致性,而列随机性矩阵则确保了算法的最优性.文献[31]和文献[32]分别论证了固定强连通和时变强连通网络情形下的收敛性,而文献[33]则是在文献[31]的基础上增加重力球动量项进一步提高算法的收敛速度.

虽然有向网络下的分布式凸优化问题已建立了很多优秀的算法,但是上述算法的控制步长都依赖于很多全局信息,比如网络伴随矩阵的最小正特征根、网络智能体个数等.此外,上述文献很少涉及到时变网络拓扑.为此,受文献[31]启发,本文拟研究一类完全分布式凸优化算法(fully distributed convex optimization algorithm,FDCOA),实现控制步长的分布式设置,即控制步长的收敛范围仅与智能体局部信息相关.进一步的,本文拟研究所设计算法在时变强连通网络下的有效性.

符号说明R表示实数集;对于实数a ∈R,[a]−=min{a,0};对于向量x=[x1··· xn]∈Rn,分别表示其中的最小值和最大值.对于向量x,y ∈Rn,x ≽y表示对于每一项都有xi≥yi,i=1,2,···,n.对于矩阵有类似定义.ln表示以自然数e为底的对数函数,简称自然对数.

2 问题描述与基础图论

2.1 图论基础知识

一个含有n个智能体的有向网络可以由符号G=(V,E)表示.其中V={1,2,···,n}表示网络智能体集,E表示网络中智能体之间通信链路组成的集合.(j,i)或j →i表明存在一条从智能体j到智能体i传输信息的有向边.智能体i0到智能体il之间存在通路即存在一组智能体且有i0→i1→···→il−1→il.也称智能体i0到il是可到达的.更进一步地,如果有向图G中所有智能体都是互相可到达的,则称G为强连通图.此外,定义智能体i的入和出邻居集分别为{j|(j,i)∈E}和={j|(i,j)∈E}.此外,默认智能体都能接收到自身的信息,即和.并令和分别表示智能体i的入度与出度.

假设1在本文所研究凸优化问题中,智能体之间的通信网络为有向强连通的.

假设1是无领导者多智能体系统分布式优化问题的必要条件,其保证了多智能体各局部信息的全局性流通,确保全局最优解的获取.

2.2 问题描述

在分布式凸优化问题中,针对每个智能体i,存在一个本地决策变量xi ∈R和一个凸成本函数fi(xi)=:R→R.该问题的目标是整个网络的成本函数之和最小,且各智能体的决策变量达到一致.所以,分布式凸优化的数学模型如下:

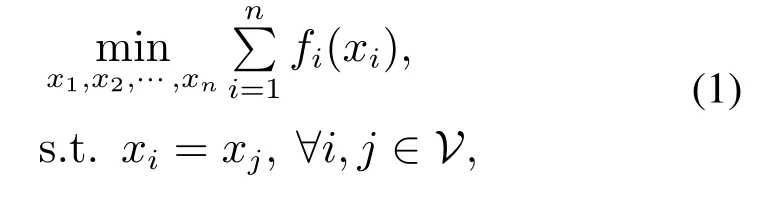
其中各智能体i只能获取自身的成本函数fi(xi).上述问题在很多应用中都可见到,比如经典的源定位问题:fi(xi)=(xi −ri)2,其中xi表示传感器i的局部估计值,ri表示传感器到目标点的测量距离.需要注意的是,本文为了行文简洁,将问题设定为一维情形.但所设计结论可直接推广至一般情形,在后续实验部分给出相应的案例仿真.

为了解决上述问题,提出以下几个假设.

假设2针对每个智能体i,假设其局部成本函数fi(xi)是严格凸的.即满足条件:(x −y)(∇fi(x)−∇fi(y))>0,∀x,y ∈R.

假设3针对每个智能体i,假设其局部成本函数fi(xi)是κi−李普希茨连续的.即满足条件:|(∇fi(x)−∇fi(y))|≤κi|x −y|,∀x,y ∈R.

假设2确保了优化问题(1)解的唯一性,同时也有利于后续算法收敛性分析.此假设要弱于文献[22,26–33]的强凸函数假设.假设3是对局部成本函数的光滑度描述,即函数的梯度不会变化太突兀,其中κi为光滑性量度.此条件对很多基于梯度下降的分布式凸优化算法的收敛性分析很重要,比如文献[16–17,19–23,25–33].此外,如定理1所示,光滑性量度κi影响算法控制参数的选取范围.

3 算法设计

为了实现控制步长的分布式设置,基于梯度跟踪技术,本文调整智能体决策变量xi的获取方式,实现余量变量的非负性.具体算法1设计如下:

本文所设计算法1与文献[31]所设计算法都解决了有向网络下的分布式凸优化问题(1),但区别点如下:1)文献[31]利用线性项,而本文算法1使用非线性项,进而实现余量si的非负;2)文献[31]使用共同的控制参数αi,且其收敛范围与网络总智能体个数、伴随矩阵关于特征根1的特征向量、和全局目标函数的光滑性量度等全局性信息相关.而本文所设计算法1控制参数仅与智能体局部邻居智能体个数和智能体局部目标函数的光滑性量度等局部性信息相关.

在给出正式的收敛性分析之前,先给出算法1中一个很重要的特性,即余量–梯度和不变性.从式(2b)可得

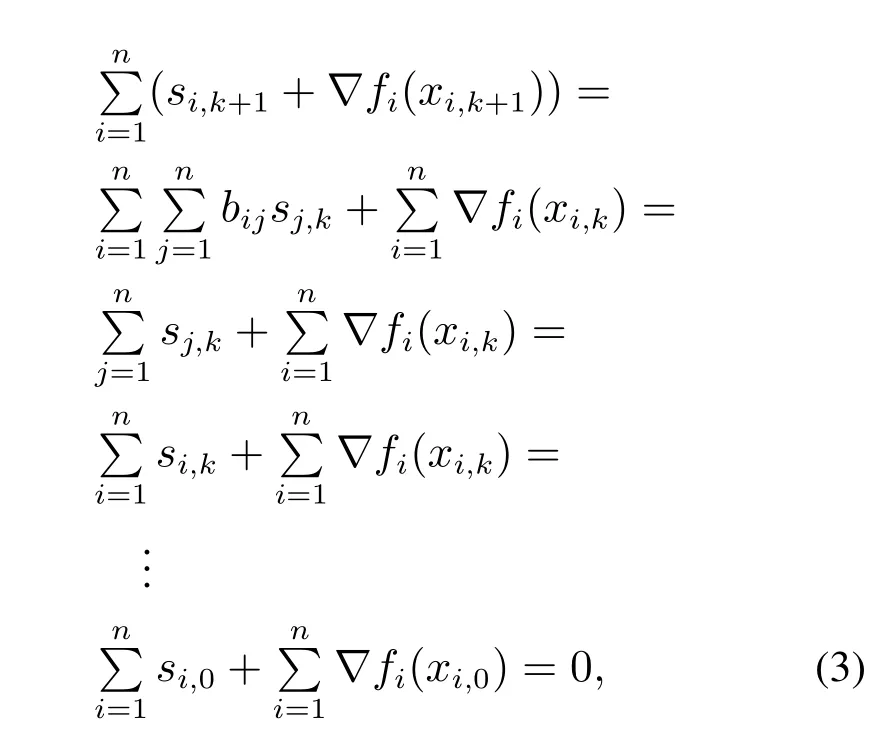
其中第2个等式的成立利用了伴随矩阵B的列随机性,最后一个等式考虑了算法的初值约束.可得结论

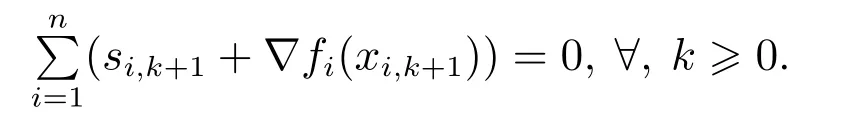
在算法1,虽然对算法初始值有约束,但是不管其形式多么复杂,只要确保局部目标函数fi(xi)是凸函数,即假设(2)成立.则此局部解都可以通过离散迭代策略xi,k+1=xi,k −β∇fi(xi,k),β >0迭代获得.此时可令智能体初始状态满足∇fi(xi(0))=0,si(0)=0即可.

4 算法收敛性分析

为了完成算法1的收敛性分析,接下来首先引入几个重要的引理.

引理1若假设1和3成立,则对任意i ∈V,k≥0和算法1,有结论

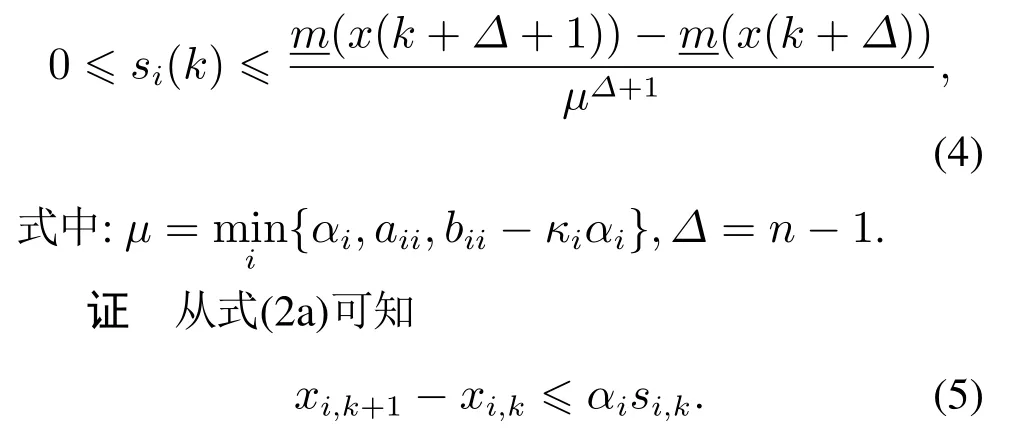
结合局部目标函数的李普希茨性质,有结论

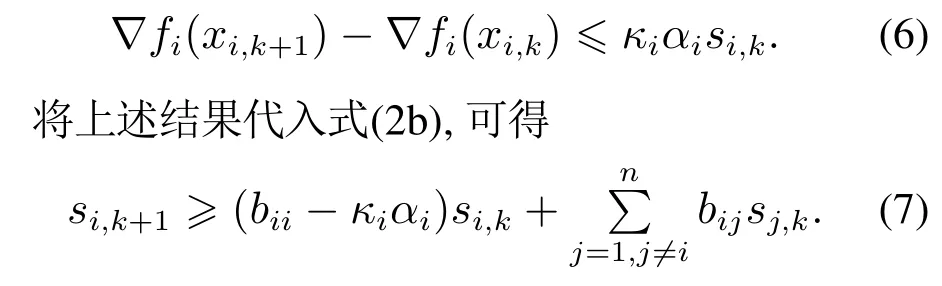
考虑到余量满足si,0=0,则余量si的非负性得以成立.进而由式(7)可推导出s(k+1)≽µ[In+S]s(k),其中矩阵S定义为Sij=1若存在通信链路(j,i)∈E.所以对于任意的k >k0≥0,有

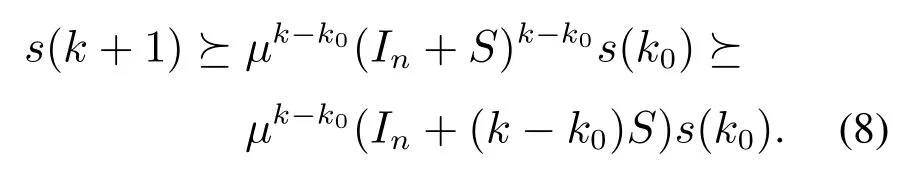
那么对于任意的i ∈V,下式成立:

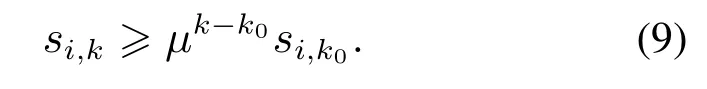
由假设1可知,对于任意两智能体i,j,存在一条有向路j →lm →···→l1→i,其中路径长度m满足m ∈{1,2,···,n −1}.结合式(7),则有

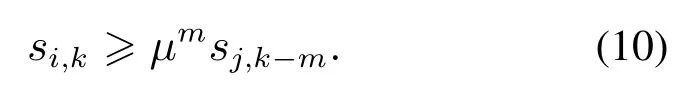
将式(9)–(10)结合,可得

引理3若假设2成立,算法1的唯一稳定点是x=x∗1n,s=0.

证首先,将上述结论xi,k=x∗,si,k=0代入算法1,可得xi,k+1=xi,k,si,k+1=si,k,这就表明上述结论是算法1 的稳定点.

接下来分析其唯一性.假设算法存在另外一组稳定点,即智能体状态不发生变化,则由引理2可知,si(k)=0.结合式(2a),可得0.则存在一智能体i1,使得,那么其所有的邻居智能体状态必满足xi,k=xi1,k,否则.进一步地,由于通信拓扑的强连通性可知,xi,k=xj,k,∀i,j ∈V.结合余量-梯度和不变性和目标函数的凸性,可知xi=x∗,∀i ∈V.

证毕.

定理1若假设1–3成立,则算法1收敛至问题(1)的最优解.不同智能体拥有不同的控制参数,且控制参数满足0<αi <.

证由引理1和式(15)可知.在引理3中,证明了系统稳定点的唯一性.接下来只需要证明对任意的智能体i,其状态xi,k极限存在即可.这就等价于证明xi,k是有界的,且不会振荡.

对于任意智能体i和k≥k0≥0,从式(2a)可得

由上述分析可知,定理1证明了算法1在固定有向强连通网络下的收敛性.接下来继续探讨该算法在时变有向强连通网络下的收敛性分析.首先给出相关的网络连通性假设.

假设4时变通信网络G(k)是周期强连通的,即存在正整数K >0,使得G([k0,k0+K])是强连通的,其中G([k0,k0+K]):=(V,∪k∈[k0,k0+K]E(k)).

为了解决时变网络下的分布式凸优化问题,算法2中的通信链路增益也需要动态改变,具体的算法2设计如下:

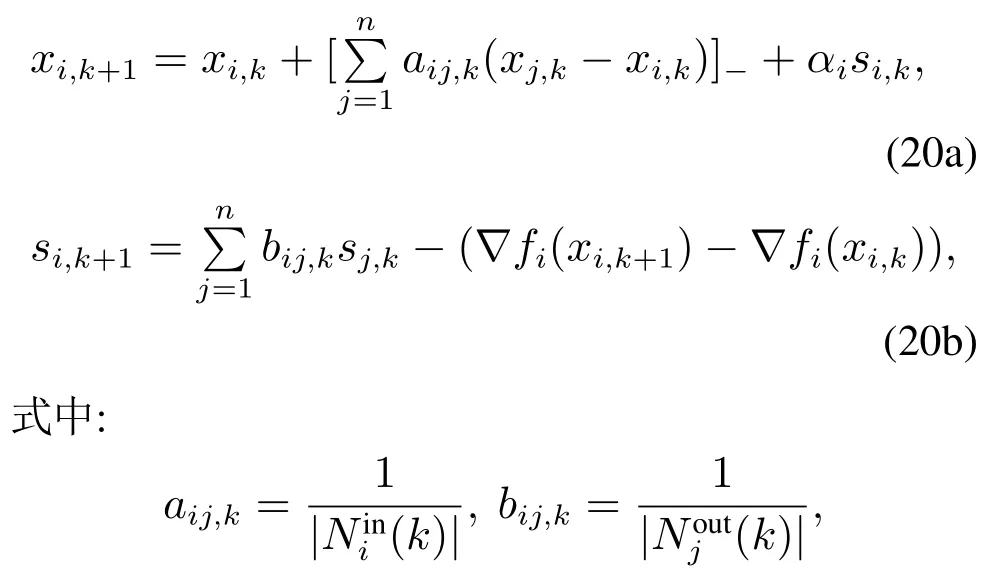
若存在(j,i)∈E,否则aij,k=0,bij,k=0;系统初始状态满足si,0=∇fi(xi,0)=0;正数αi是控制参数.

推论1若假设1,2和4成立,则算法2收敛至问题(1)的最优解.不同智能体拥有不同的控制参数,且控制参数满足0<αi <.

证由算法2可以看出,只需对引理2进行调整即可.由假设4可知存在正整数K >0,使得G([k0,k0+K])满足强连通.所以引理2的∆调整为∆=K(n−1).由于后续证明是相似的,故在此不再赘述.

证毕.

5 案例分析

为了验证所提算法的有效性,接下来本文利用MATLAB演示3个案例的仿真效果.

案例1首先考虑由4个多智能体组成的有向网络分布式凸优化问题[16],每个智能体的局部成本函数定义为

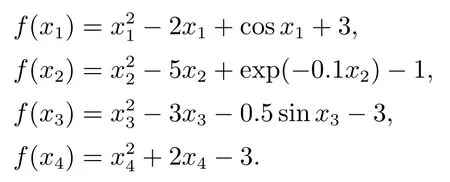
智能体间的通信链路如图1所示.由算法1可知,智能体i只需要将自身信息xi,k和bjisi,k发送给其邻居智能体j.

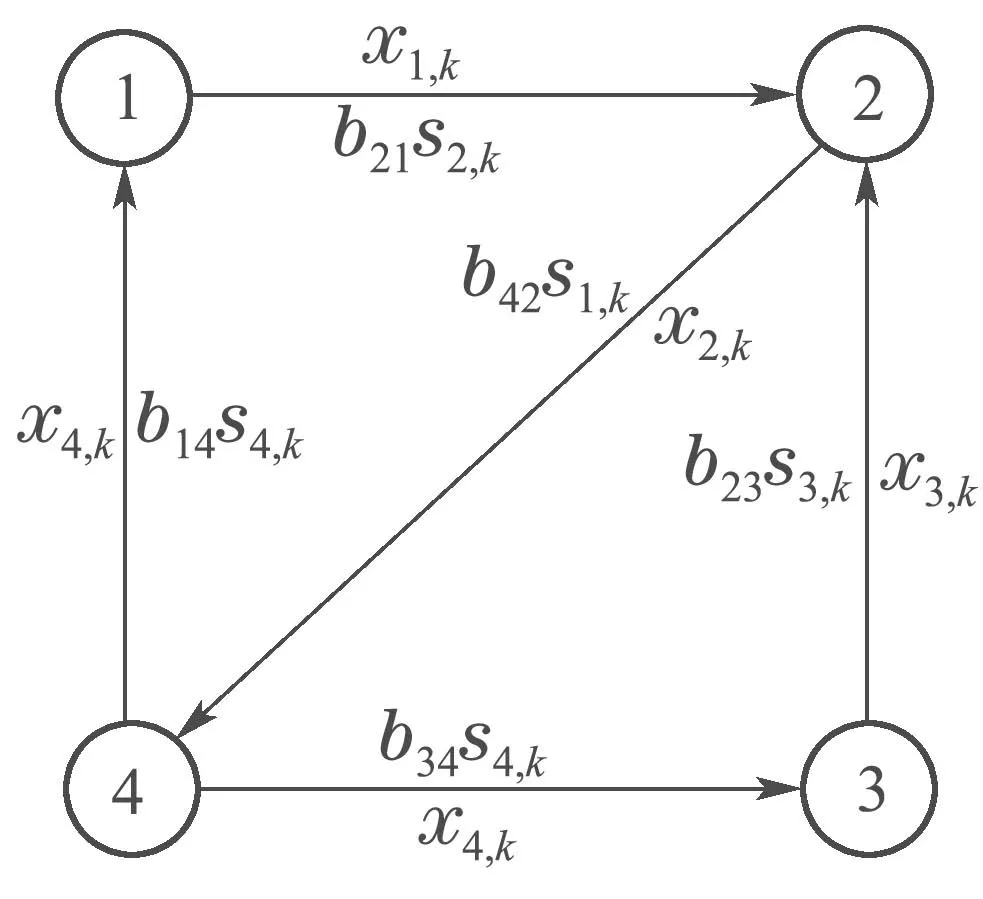
图1 4智能体系统通信网络Fig.1 The communication network for four agents

如算法1所示,首先获取各局部成本函数驻点x(0)=[1.4987,2.5388,1.5141,−1],且案例问题的最优解为x∗=1.1508.令αi=,∀i ∈V,算 法1运行轨迹如图2和3所示.从图2可看出,各智能体协同收敛至最优解x∗.从图3可以看出,算法1所设计的余量控制策略可确保变量si的非负性,且最终都趋向于零.此外,从前面的控制步长αi的选取可以看出,本文所设计算法1实现了控制步长的分布式选取,即只需利用各智能体局部信息,克服了同类分布式算法中控制步长选取困难的问题.进一步,为了验证算法2的有效性,基于上述数据,考虑如图4所示的通信网络.将算法1在图1与算法2在图4下的误差

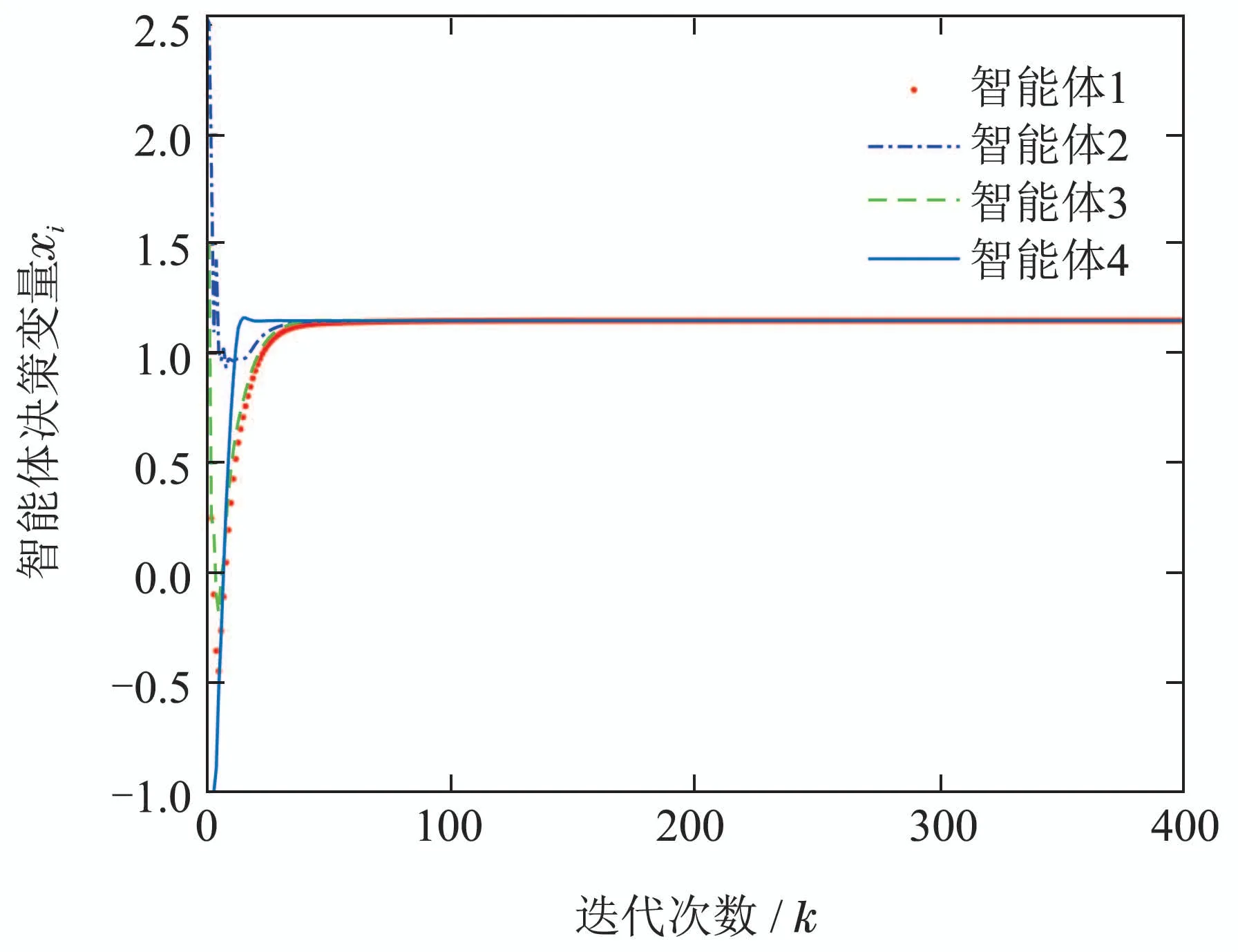
图2 案例1中各智能体状态xi轨迹图Fig.2 The trajectories of state variable xi for each agent in case 1

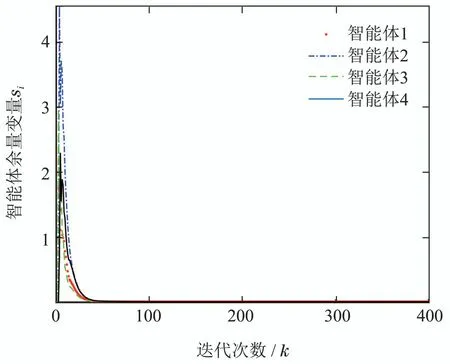
图3 案例1中各智能体余量si轨迹图Fig.3 The trajectories of surplus variable si for each agent in case 1

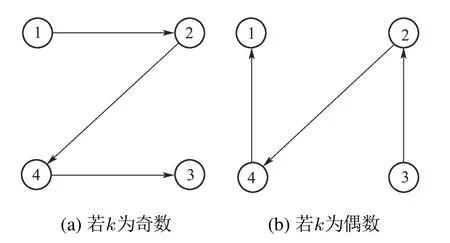
图4 4智能体时变强连通网络Fig.4 The communication network for four agents

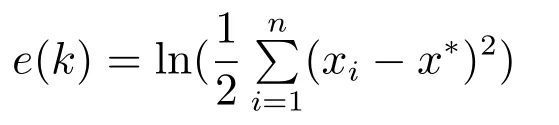
展示在图5中.从图5可以看出,本文所设计算法在时变强连通网络下亦是有效的,且固定通信网络下收敛速度相对更快一点.

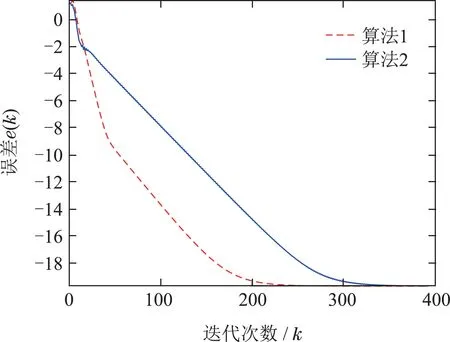
图5 案例1中两种算法误差ei轨迹图Fig.5 The convergence comparison between the two proposed algorithms in case 1

案例2验证本文所设计算法1在大规模网络下的有效性.以文献[32]的分布式最小二乘问题为例,各智能体协同寻找最小二乘问题的解,其中局部损失函数定义为,在此案例中,令智能体个数为n=500,Hi ∈R2×1.智能体间的通信拓扑如图6所示.算法1决策变量运行轨迹如图7所示,各智能体协同收敛到最优解.同案例1,算法运行误差轨迹图如图8 所示.虽然文献[32]矩阵奇异摄动法证明了所设计算法在时变网络下的收敛性,但没有给出控制步长的收敛范围,且各智能体拥有相同的控制步长,不利于分布式系统的实际应用.

图6 案例2中500智能体系统通信网络Fig.6 The communication network for 500 agents in case 2

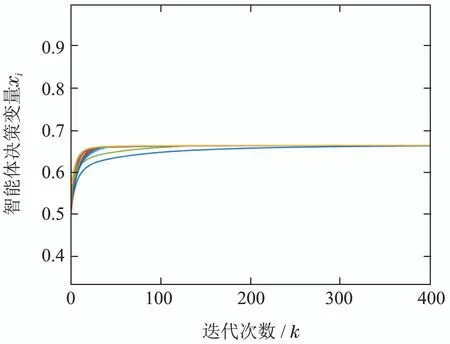
图7 案例2中各智能体状态xi轨迹图Fig.7 The trajectories of state variable xi for each agent in case 2

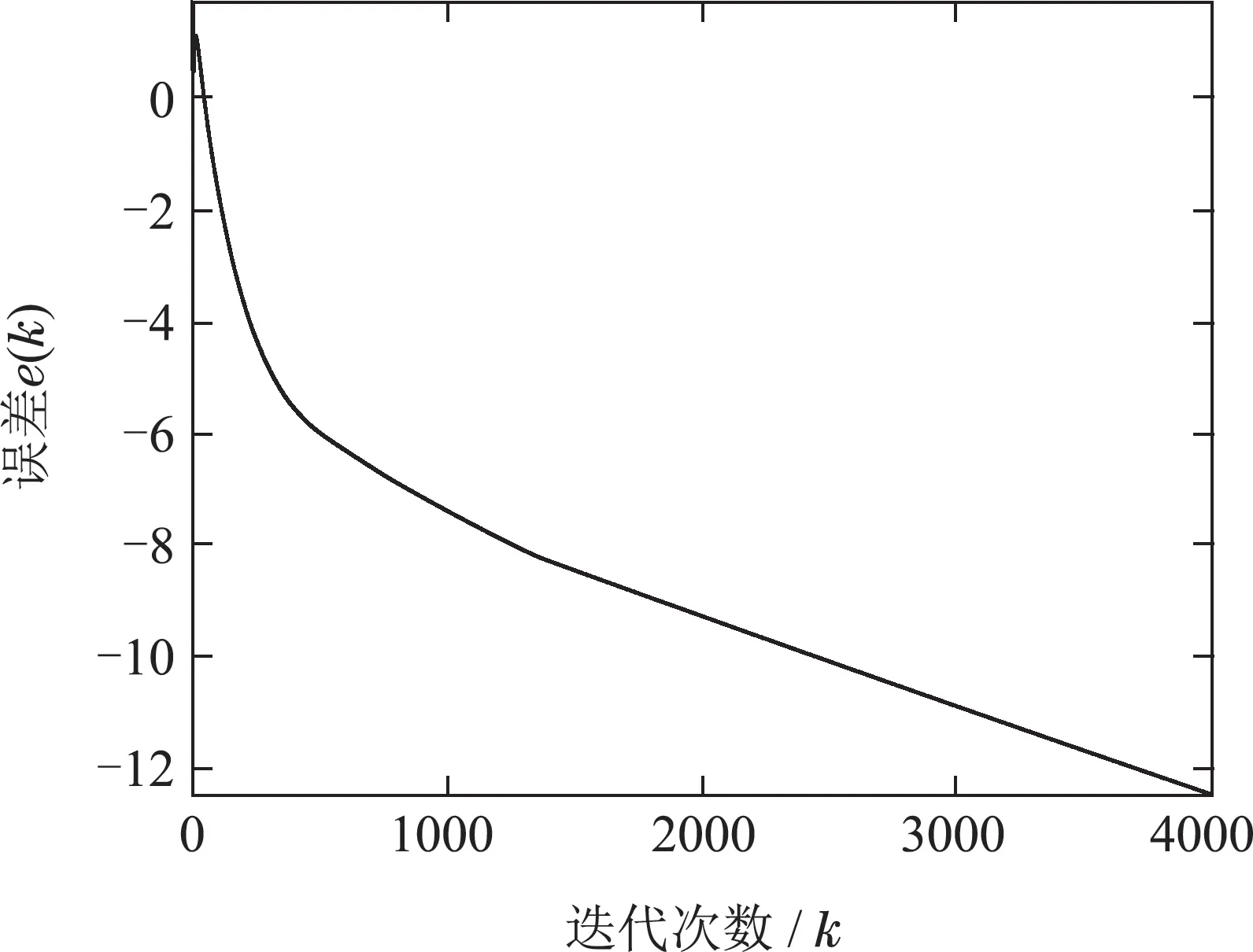
图8 案例2中误差e(k)轨迹图Fig.8 The trajectory of error e(k)in case 2

案例3为了验证本文所提算法在一般维度情形下分布式凸优化问题的有效性,如文献[34]所示的二次布局问题(quadratic placement problem),包含5个固定点和4个自由点,其中固定点分别为t1=(−1,−1)T,t2=(−1,0)T,t3=(0,1)T,t4=(1,0)T,t5=(1,−1)T,自由点的初始状态为x2(0)=(1,−0.5)T,x3(0)=(0.5,0.5)T,x4(0)=(−0.5,0.5)T.自由节点的通信网络如图1所示.此外,自由点的目标函数设置为

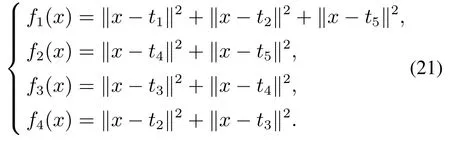
可以得出κ1=6,κ2=κ3=κ4=4.此外上述优化问题的理论最优解为x∗=,自由点的状态变化如图9所示.可以看出,本文所设计算法对一般维度情形分布式优化问题亦是有效的.

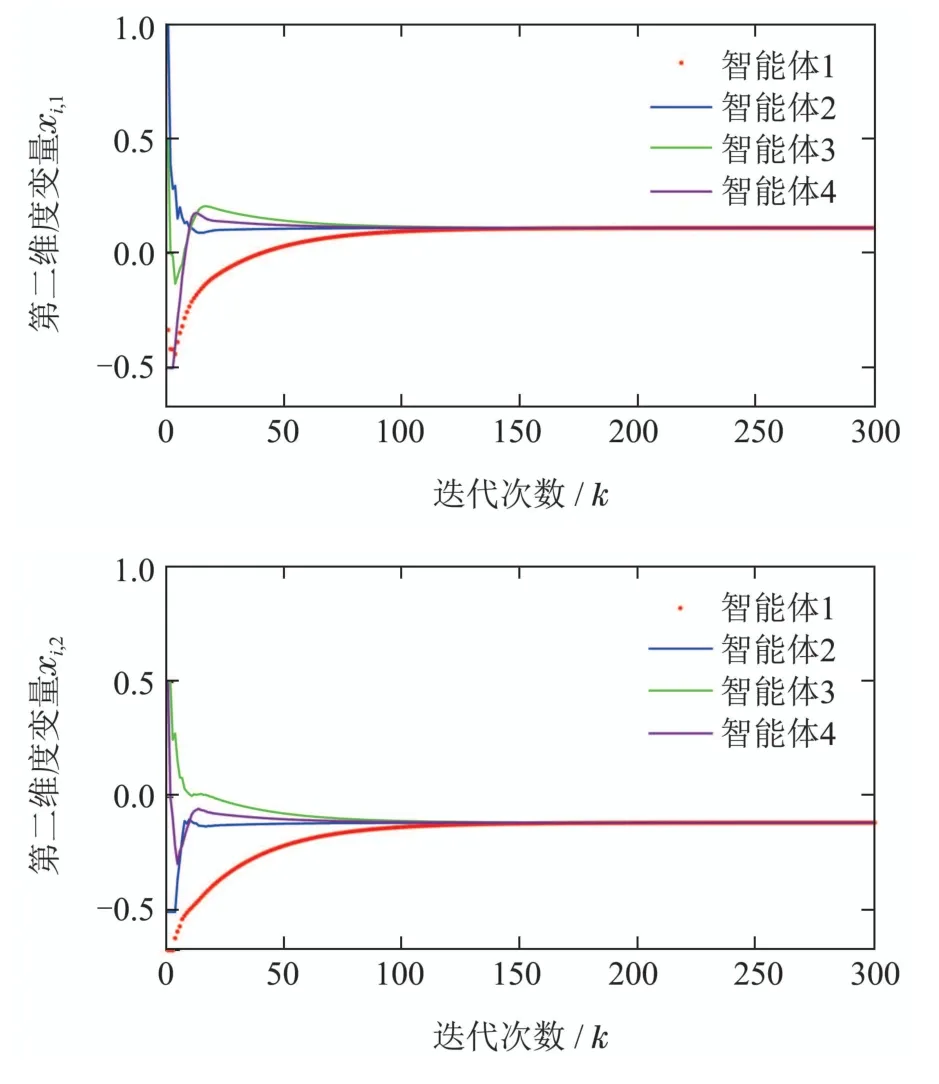
图9 案例3中各智能体状态xi轨迹图Fig.9 The trajectories of state variable xi for each agent in case 3

6 结论

本文针对非平衡有向强联通网络下的分布式凸优化问题,提出了一种完全分布式优化算法.在算法设计中,每个智能体只能获取自身的成本函数信息.通过调整智能体决策变量的迭代策略,实现了余量变量的非负性控制和控制步长的分布式设置.其次,本算法对时变强连通网络亦是有效的.仿真结果表明,本文所设计算法可以有效解决有向网络下的凸优化问题.