惯量积测试系统再平衡回路设计

张 超,周晓俊,2,凌林本

（1.北京航天控制仪器研究所,北京 100039;2.北京航空航天大学仪器科学与光电工程学院,北京 100191）

0 引言

摆式积分陀螺加速度计是惯性制导平台系统中不可缺少的核心测量仪表,其结构类似于一个沿自转轴方向附加偏心质量的二自由度陀螺仪,具有陀螺仪和摆的双重特性,是一种利用陀螺力矩进行反馈的摆式加速度计［1］。由于摆式积分陀螺加速度计存在以二次项误差为主的非线性误差项,制导系统误差模型中未对其进行补偿,实际飞行结果分析显示,存在制导工具误差偏大、误差模型不完善造成“天地不一致”等问题。

在摆式积分陀螺加速度计的误差模型中,二次项误差主要是由浮子组件的不等惯量和惯量积引起的。其中,不等惯量引起的非线性误差项与内环零位偏角相关,可以通过在电气上减小内环零位偏角抑制该项误差。所以,惯量积是引起非线性误差项的主要因素。惯量积是由结构决定的,工程上难以避免,必须在精确测试的基础上进行补偿。

惯量积测试属于惯性参数测量范畴,但国内外报道多以转动惯量、质心位置测试为主。目前,该方面设备主要应用于空间飞行器部件、汽车动力部件、发动机部件等外形规则的大型物体测量过程中。关于惯量积测试方法和测试理论的研究,国内外未见报道。

针对惯量积量级小（10-9kg·m2～10-8kg·m2）,常规手段测试难度大,本文提出了一种惯量积测试的方法。通过浮子组件高速旋转激发惯量积产生离心力矩,并设计再平衡回路产生再平衡力矩,运用力矩平衡的方法使浮子组件处于平衡状态,根据力矩电流的大小即可得到浮子组件惯量积产生的离心力矩的大小。

1 惯量积测试原理

摆式积分陀螺加速度计的功能是测量沿外框架轴的视加速度。当沿外框架轴有视加速度输入时,摆式积分陀螺加速度计的转子将绕外框架轴进动,其进动角速度与输入的视加速度成正比。摆式积分陀螺加速度计浮子组件为近似圆柱体,如图1所示。oxz为与浮子组件固联的坐标系,质心m偏离浮子轴线的距离为l。浮子组件通常采取对称设计,惯量积主要是由实际零件加工、装配中的误差导致的,如圆周对称位置存在微小质量偏差m′时会产生不影响摆性的惯量积Jxz

图1 浮子组件惯量积示意图Fig.1 Diagram of floater assembly inertia product

Jxz=2m′b2sinθ0cosθ0（1）

式（1）中,b为质量偏差m′到原点o的距离,θ0为质量偏差m′与oz轴的夹角。

浮子组件惯量积是陀螺加速度计产生二次项误差的重要因素。虽然惯量积量级小,约为10-9kg·m2～10-8kg·m2,但是对仪表精度影响显著,10-8kg·m2的惯量积产生的仪表非线性误差项为10-5量级。精确测量惯量积并进行结构优化调整是消除仪表二次项误差的基础。

陀螺加速度计浮子组件惯量积小,精确测试难度大,利用角度传感器等电磁元件,通过借助高速旋转条件,放大惯量积产生的离心力矩,通过测试离心力矩大小,实现微小惯量积的精确测试。测试基本原理为:在浮子组件存在惯量积的情况下,当浮子组件绕输入轴x以角速度ω转动时,在输出轴y上会产生离心力矩

通过再平衡回路产生大小相等、方向相反的再平衡力矩使浮子组件处于平衡状态,此时该离心力矩正比于再平衡回路的力矩电流。通过测量力矩电流即可得到离心力矩,进而得到惯量积Jxz的值。惯量积的测试示意图如图2所示,其工程实现主要采用高精度速率转台,被测浮子组件采用气浮方式悬浮支撑,通过高精度工装固定在转台上,并实现转轴与浮子轴线的对准。

图2 惯量积测试示意图Fig.2 Diagram of inertia product measurement

2 再平衡回路设计

再平衡回路广泛应用于惯性仪表中,使仪表工作于闭环状态。通过产生再平衡力矩,使仪表输出轴上的力矩之和为零,从而保持仪表输出轴相对于壳体始终处于静止状态,并通过力矩电流大小获得仪表输入值［2-4］。

按施加电流的形式,再平衡回路可以分为模拟再平衡回路和脉冲再平衡回路。模拟再平衡回路结构简单,易于实现,力矩电流是连续变化的模拟量,通过I/F电路将模拟的电流信号转换成脉冲信号输出给导航计算机。脉冲再平衡回路结构复杂,脉冲信号由直流信号和三角波信号比较而成,施加的力矩电流是幅值一定、周期一定、宽度可调的脉冲信号［5-7］。随着DSP和FPGA等电子技术的不断发展,产生了一种全新的数字式再平衡回路,脉冲信号的产生和控制算法集中于数字芯片中,能直接实现脉冲加矩和数字输出［8-10］。基于全数字式再平衡回路的优势,采用以DSP为核心的全数字式再平衡回路方案。

2.1 再平衡回路工作原理

当浮子绕输入轴x转动时,由于惯量积的存在,会产生一个绕输出轴y的离心力矩,使浮子绕输出轴y转动而偏离零位,角度传感器检测浮子角偏移并转变成载波信号,经过前置放大、带通滤波、相敏解调和低通滤波等环节后,得到正比于浮子偏转角的电压信号。该电压信号经过A/D转换后送入数字处理器,经过控制算法产生控制量,输出调宽的脉冲波,作用于H开关和恒流源。给力矩器施加电流,力矩器产生的电磁力矩恰好与惯量积产生的离心力矩平衡,从而使浮子组件始终保持在零位附近,如图3所示。数字控制器输出的调宽脉冲波的占空比反映了惯量积产生的绕输出轴的离心力矩的大小。

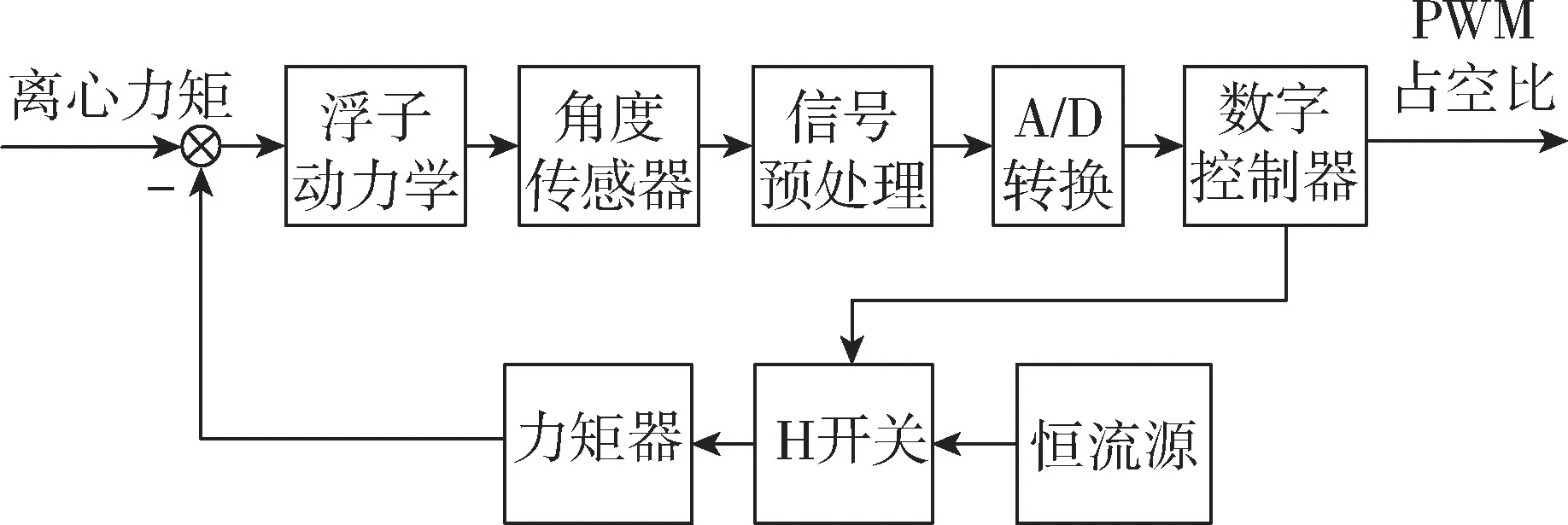
图3 再平衡回路工作原理图Fig.3 Diagram of rebalance loop operation principle

整个再平衡回路由信号预处理电路、数字控制电路和力矩电流发生器组成。其中,信号预处理电路包括前置放大、带通滤波、相敏解调和低通滤波,这部分电路的作用主要是对传感器输出的信号进行放大、解调和滤波,并且使信号幅值位于A/D转换的量程范围内。数字控制网络的核心是DSP,主要功能是进行A/D转换、控制器的数字实现和PWM波输出。力矩电流发生器包括恒流源和H开关两部分,主要功能是供给力矩器调宽的脉冲电流信号产生再平衡力矩,使浮子始终处于零位附近。

2.2 再平衡回路模型建立

由2.1节可知,再平衡回路主要由三部分组成,下面对整个系统进行建模。浮子角运动与外加力矩之间的微分方程为

式（3）中,M为浮子上的外加力矩,C为阻尼系数,K为弹性系数,Jy为浮子相对于输出轴的转动惯量,β为浮子偏转角。

对于本文研究的系统来说,弹性系数为零。由于采用气浮轴承,阻尼系数近似为零,因此式（3）在初始状态为零的条件下,经过Laplace变换后,动力学传递函数为

式（4）中,Jy=9×10-5kg·m2。

回路中,传感器的灵敏度为Ks=34V/rad,前置放大、带通滤波、相敏解调简化为比例环节K1=40,数字控制器输出的电压转电流系数为KVI=0.025A/V,力矩器系数为KM=2.45×10-4N·m/A,低通滤波器传递函数为Gf（s）

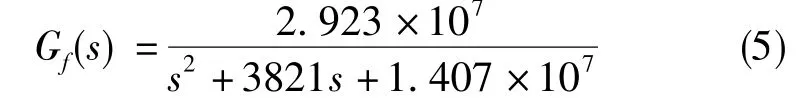
再平衡回路的框图如图4所示,M为惯量积产生的绕输出轴的离心力矩,Mq为再平衡回路产生的平衡力矩,Gc（s）为控制器,I为加到力矩器的电流。

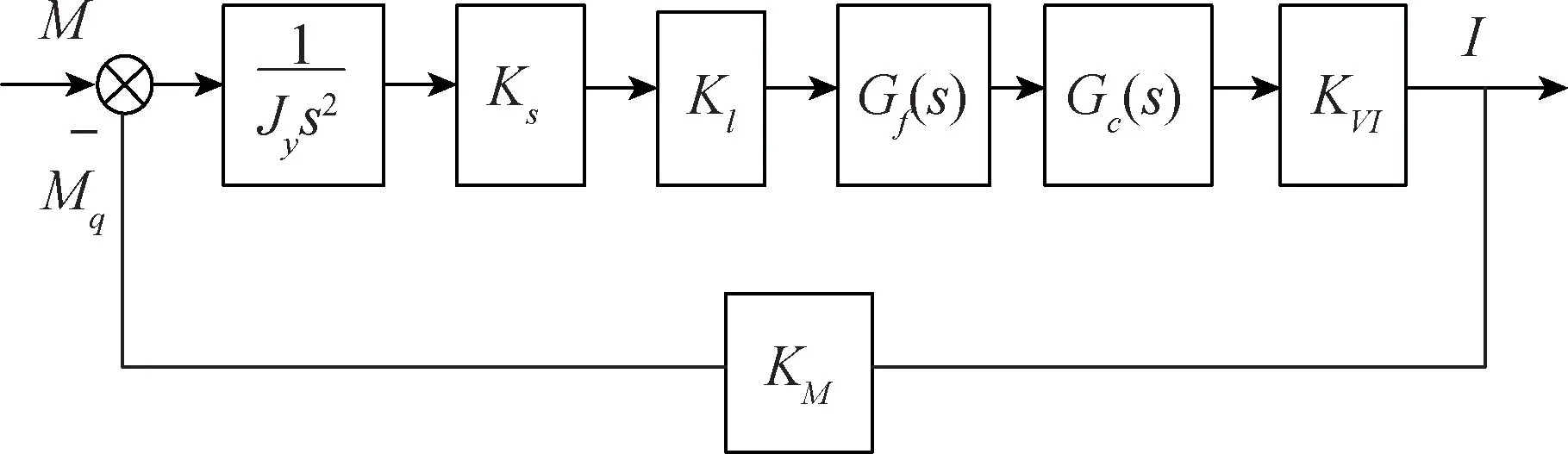
图4 再平衡回路的框图Fig.4 Block diagram of rebalance loop

不加控制器时,系统的开环传递函数为

系统的开环频率特性如图5所示。

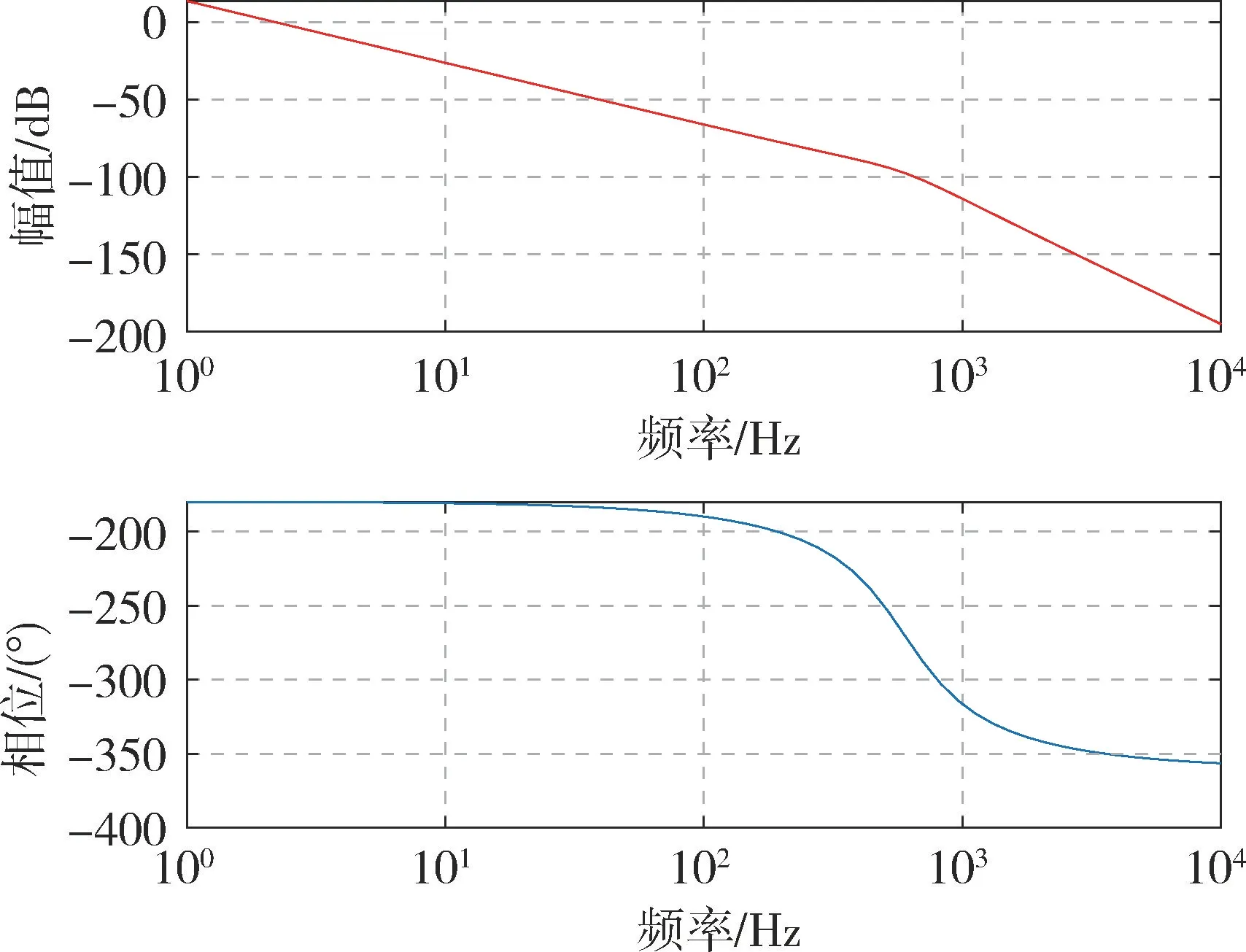
图5 系统开环频率特性Fig.5 Diagram of open-loop frequency characteristics

由图5可知,系统中频段相位滞后较大,导致系统超调量过大,且系统截止频率较低,系统响应较慢。因此,需要设计控制器使系统具有良好的动态特性和静态指标。

2.3 控制器设计

PID控制器是一种线性控制器,它根据给定值r（t）与实际输出值y（t）构成偏差e（t）,将偏差的比例（P）、积分（I）和微分（D）通过线性组合构成控制量,对受控对象进行控制。其控制规律为

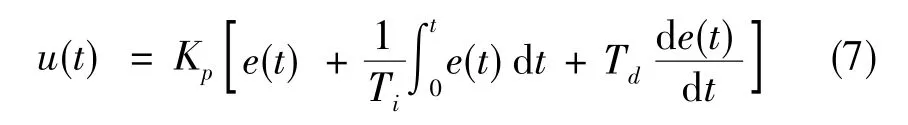
式（7）中,e（t）为输入的误差信号,Kp为比例系数,Ti为积分时间常数,Td为微分时间常数,u（t）为控制器输出。

传递函数形式为

对式（7）做离散化处理就可以得到位置式数字PID控制算法,即以一系列的采样时刻点kT代表连续时间t,以矩形法数值积分近似代替积分,以一阶向后差分近似代替微分,可得到其k采样时刻的离散PID表达式

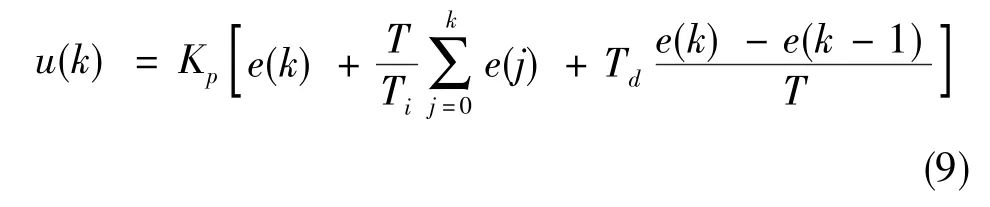
式（9）中,T为采样时间。

根据式（9）应用递推原理,可得到k-1个采样时刻的输出

式（9）与式（10）相减,经整理后,可以得到增量式PID控制算法公式

式（12）中,Ki=Kp/Ti,Kd=KpTd。

由再平衡回路原理可知,再平衡回路不仅是锁定回路,而且是测量回路。作为锁定回路,应具有足够的跟踪能力,即能够输出足够大的力矩电流使浮子维持在零位附近;作为测量回路,应使输出的力矩电流正确反映输入力矩。为满足再平衡回路的要求,必须提高系统截止频率,增加系统相位裕度,在控制器中需要加入微分环节;为使浮子偏转角度在稳态时为零,需要在控制器中加入积分环节。选取增量式PID参数:Kp=7.45、Ki=22.9、Kd=0.394、T=5×10-4s。

根据增量式PID控制律以及控制思想,设计控制流程图如图6所示。

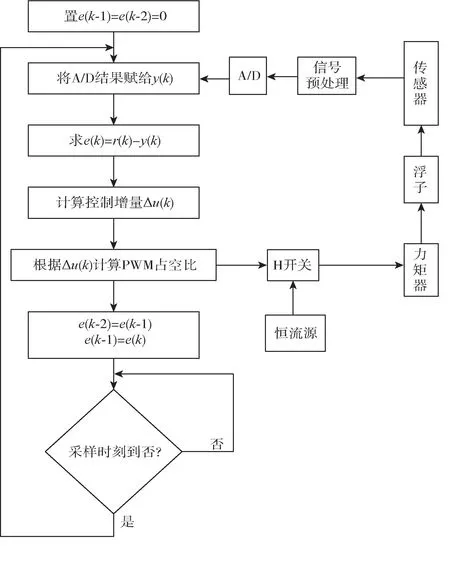
图6 增量式PID控制流程图Fig.6 Flowchart of incremental PID control

3 仿真和实验结果

为验证再平衡回路的性能,对设计的电路进行系统仿真,系统采样频率为2kHz。加入控制器后,闭环系统零极点分布如图7所示,闭环极点全部位于单位圆内,系统处于稳定状态。

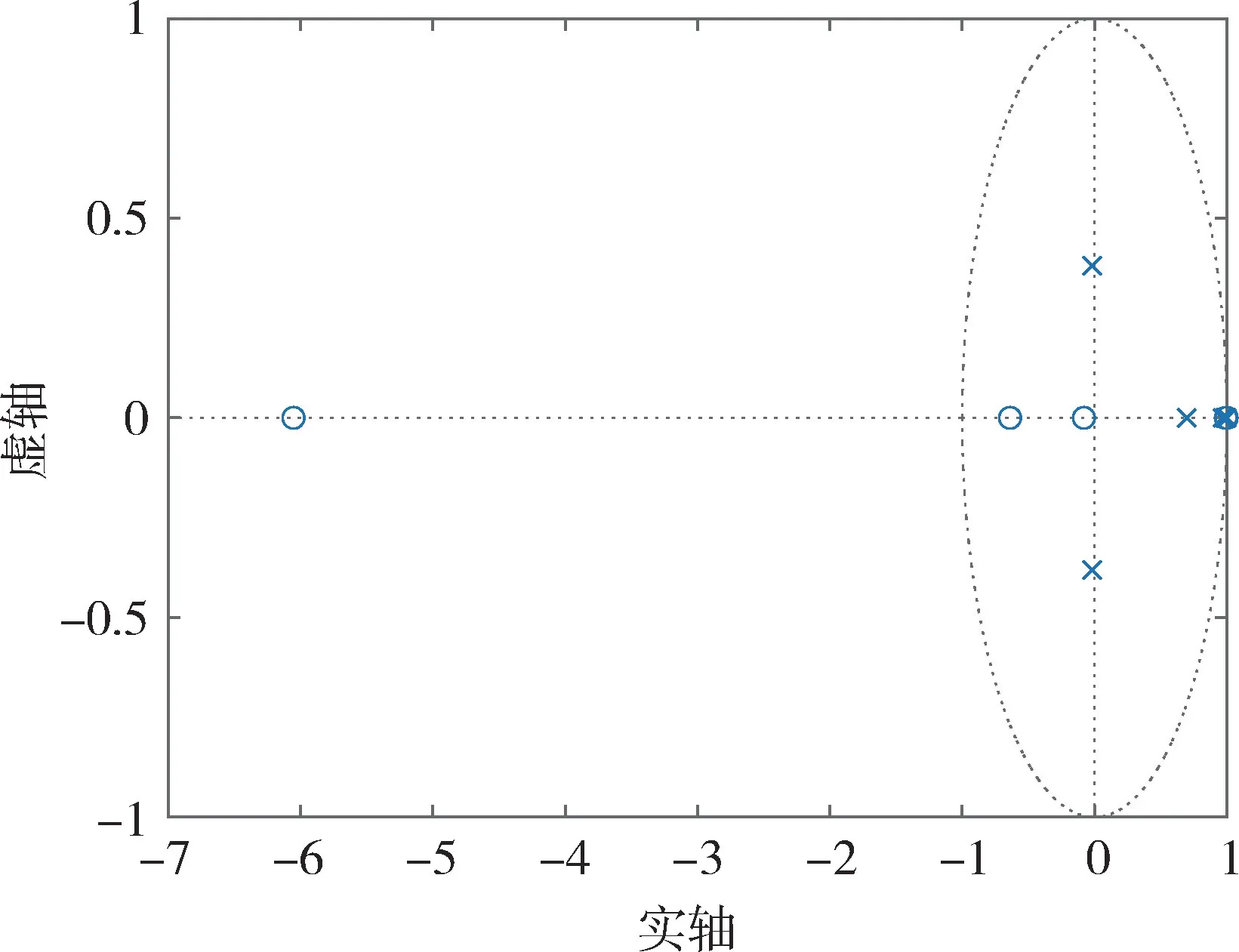
图7 闭环系统零极点分布图Fig.7 Zero-pole distribution diagram of closed-loop system

开环频率特性如图8所示,系统开环截止频率为12.7Hz,相角裕度为69°,幅值裕度为27.3dB。

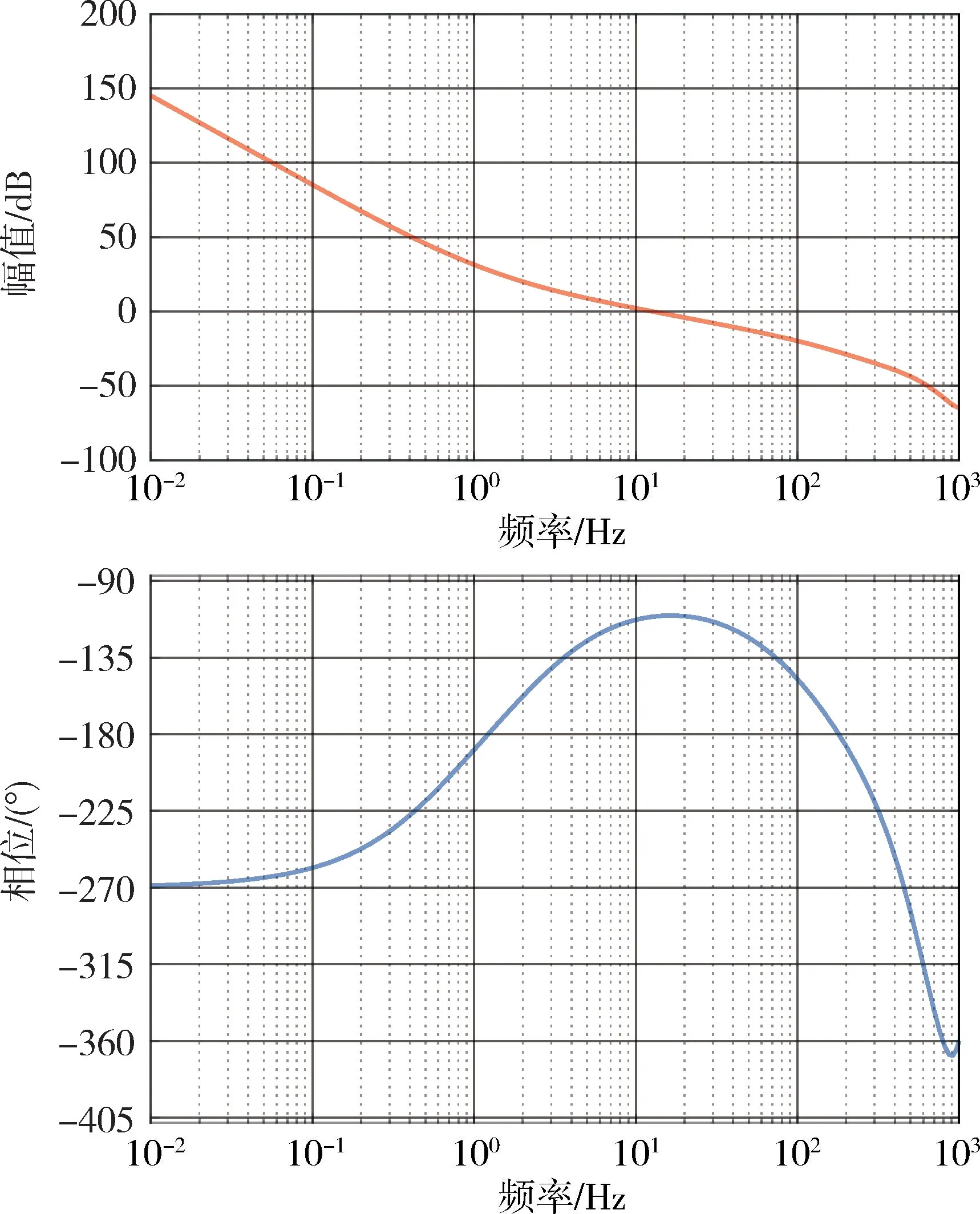
图8 加入控制器后系统开环频率特性Fig.8 Diagram of open-loop frequency characteristics with controller

系统闭环频率特性如图9所示。由图9可知,闭环初始值为0dB,所以在阶跃信号作用下,系统没有静差;幅频特性曲线峰值较小,系统阶跃响应过程的超调量小,同时系统带宽为17.7Hz,系统具有较快的响应。

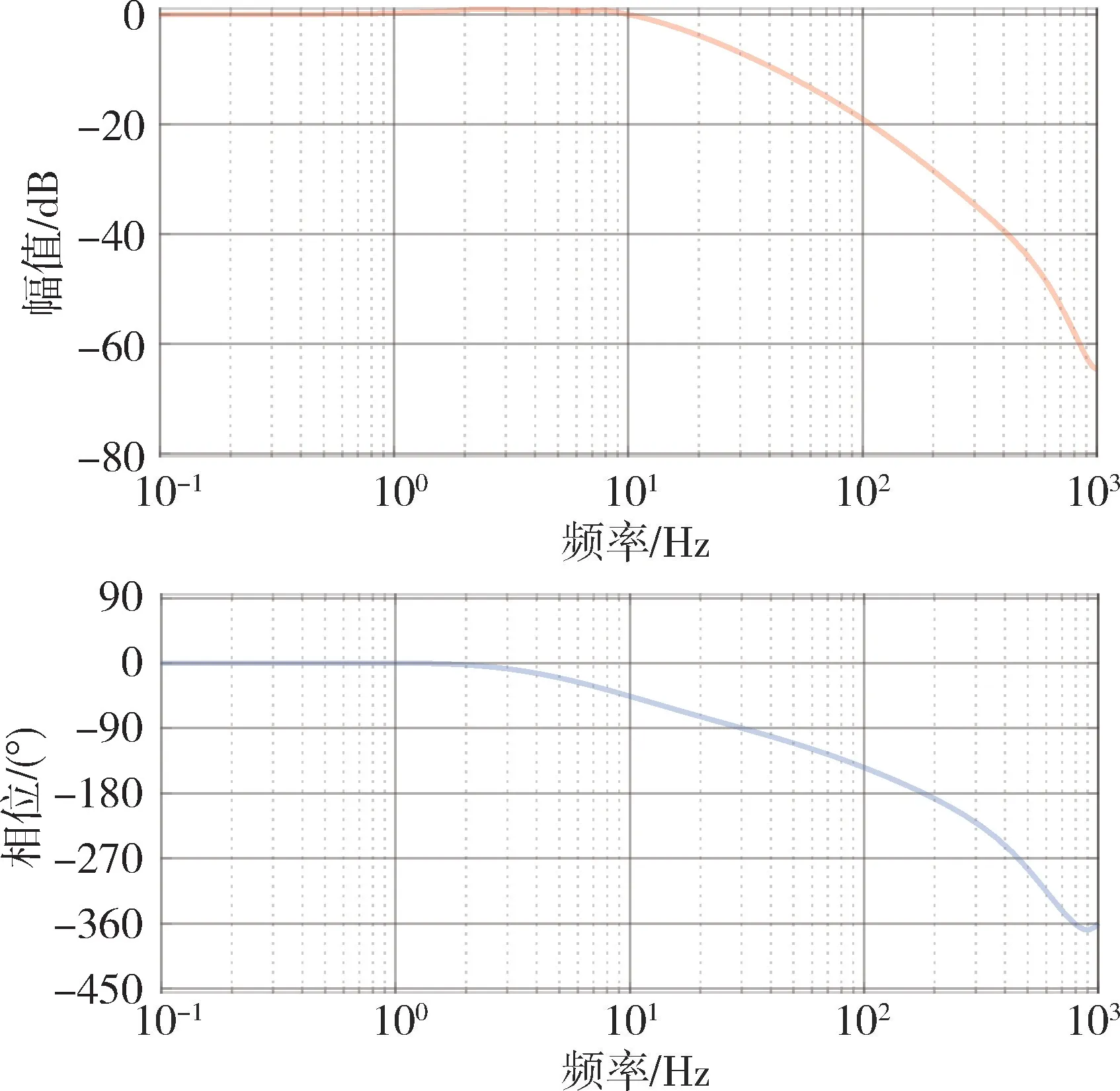
图9 系统闭环频率特性Fig.9 Diagram of closed-loop frequency characteristics

在输入最大离心力矩5×10-5N·m的条件下进行仿真,DSP输出的PWM占空比曲线如图10所示。由图10可知,系统调节时间为0.15s,超调量为15.7%,系统响应较快且过渡过程比较平稳。力矩电流大小曲线如图11所示。由图11可知,再平衡回路能提供足够大的力矩电流。

图10 PWM占空比曲线Fig.10 Curve of PWM duty ratio

通过采样电阻对力矩电流进行采样,采样电阻选择精密无感电阻,电阻大小为5Ω,精度为千分之一,设计的恒流源大小为253.7mA。采样电阻两端的电压值与其对应的占空比如表1所示。通过对采样数据进行处理可得,力矩电流发生器的零偏电流为0.164mA,力矩电流非线性度小于0.5%,力矩电流的对称性小于0.2%。通过采样电压值与理论值相比,可得采样电压的最大误差小于1mV,对应力矩电流的误差为0.2mA。在转速为300r/min的条件下,可以满足惯量积测试精度10-9kg·m2的要求。

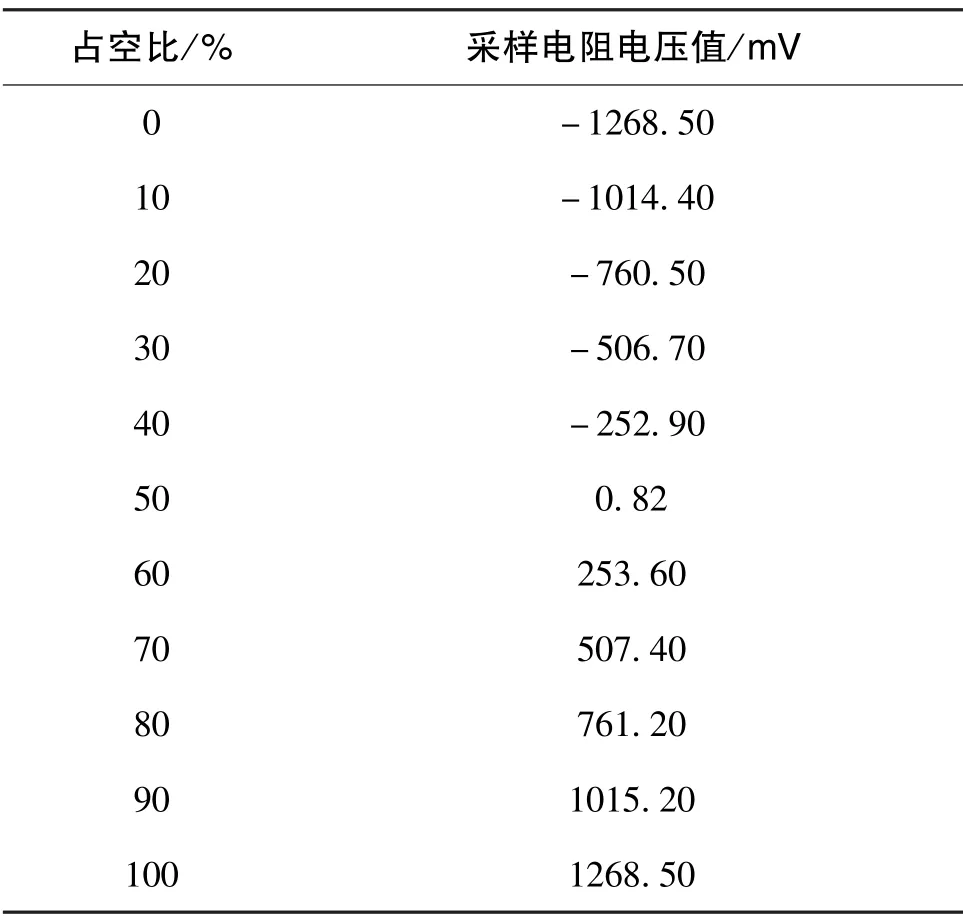
表1 采样电阻的电压值与对应的占空比Table1 Voltage value of sampling resistance and its corresponding duty ratio

4 结论

本文提出了一种通过高速旋转激发惯量积产生离心力矩的测试方法,并设计了全数字式再平衡回路来测量离心力矩。通过仿真分析,所设计的再平衡回路不仅能提供足够的力矩电流使浮子组件始终处于零位附近,而且系统响应快,过渡过程比较平稳,输出的力矩电流能正确反映惯量积产生的离心力矩,惯量积测试精度优于10-9kg·m2。通过精确测量惯量积并进行结构优化调整,为摆式积分陀螺加速度计精度提高打下基础。