VARTM的边缘效应数值模拟研究

穆文博，严 波

(上海交通大学 材料科学与工程学院，上海 200030)

0 引 言

随着现代工业朝着轻量化设计、整体化成型和数字化制造的不断发展，真空辅助树脂传递模塑(VARTM)作为一种制备高性能树脂基复合材料制件的成型工艺逐渐发展起来。VARTM也是成型带有加筋、夹芯、嵌体或预埋件等大型结构复杂构件的理想工艺[1-3]。但是，VARTM存在的边缘效应，导致树脂流速快的区域浸润不充分，流动太慢的区域树脂富集，从而破坏了模具型腔的填充模式。目前对于VARTM成型工艺的研究并不充分，用于预测与优化VARTM成型过程中树脂流动行为的数值仿真技术也不成熟[4-6]。且一些VARTM成型还主要是通过试错法来进行工艺参数设计和制件质量估计，误差较大而且成本高。采用数值模拟技术预测VARTM工艺过程中的树脂流动状况，进而优化工艺参数、提高制件质量是数字化低成本制造VARTM制件的重要手段[7-8]。

本文基于达西定律建立VARTM树脂充填流动过程的中面模型，并开发相应的数值模拟软件，并将模拟结果与实验结果进行对比，研究浇口对带内孔的纤维预制体内的树脂充填过程中的边缘效应的影响，预测和分析干斑位置。

1 计算模型与数值模拟软件开发

一般常用达西定律来描述流体穿过多孔介质的流动[9-10]。VARTM成型过程中的树脂三维流动，沿着厚度方向的流动需要考虑重力分量的影响，因此树脂流过纤维预制体的过程采用达西定律可以表示为:

(1)

式中，ui为树脂在纤维预制体中的流动速率，φ为纤维织物的孔隙率，η为树脂黏度，P， i为压力梯度，ρ为树脂密度，gi为重力加速度分量。ki为纤维预制体的渗透率。结合不可压缩流体的连续性方程可以得出树脂流动的控制方程为：

(2)

树脂流动的边界条件为：

(1) 流前压力条件为型腔真空压力；

(2) 入口的压力条件为恒压状态，一般为1个标准大气压；

(3) 树脂不能穿透模具壁。

使用伽辽金加权余量法建立树脂流动控制方程的有限元方程积分形式：

(3)

式中，w为权函数，Ω为求解域。在中面模型中，式(3)分解为厚度方向积分和平面方向上的积分，因此中面模型的树脂流动有限元计算公式为：

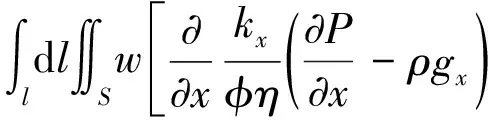
(4)

式中，l为单元厚度方向，S为单元平面，x、y为平面方向的坐标系分量。

求解中面模型的有限元方程式(4)可以计算树脂流动过程中的压力场和流动速度。然后利用流体体积(VOF)法确定流动前沿和填充时间步长。由此开发的C++数值模拟软件的计算流程如图1所示。为预测VARTM工艺中出现的干斑位置，为浇口、工艺设计提供依据，本模拟软件提出了预测空隙的算法：在树脂充填流动的计算过程中，存储不同位置的充填时间，充填结束之后，判断每个位置(如网格节点)的充填时间是否大于周围节点的充填时间，如果是，则该节点为干斑位置。

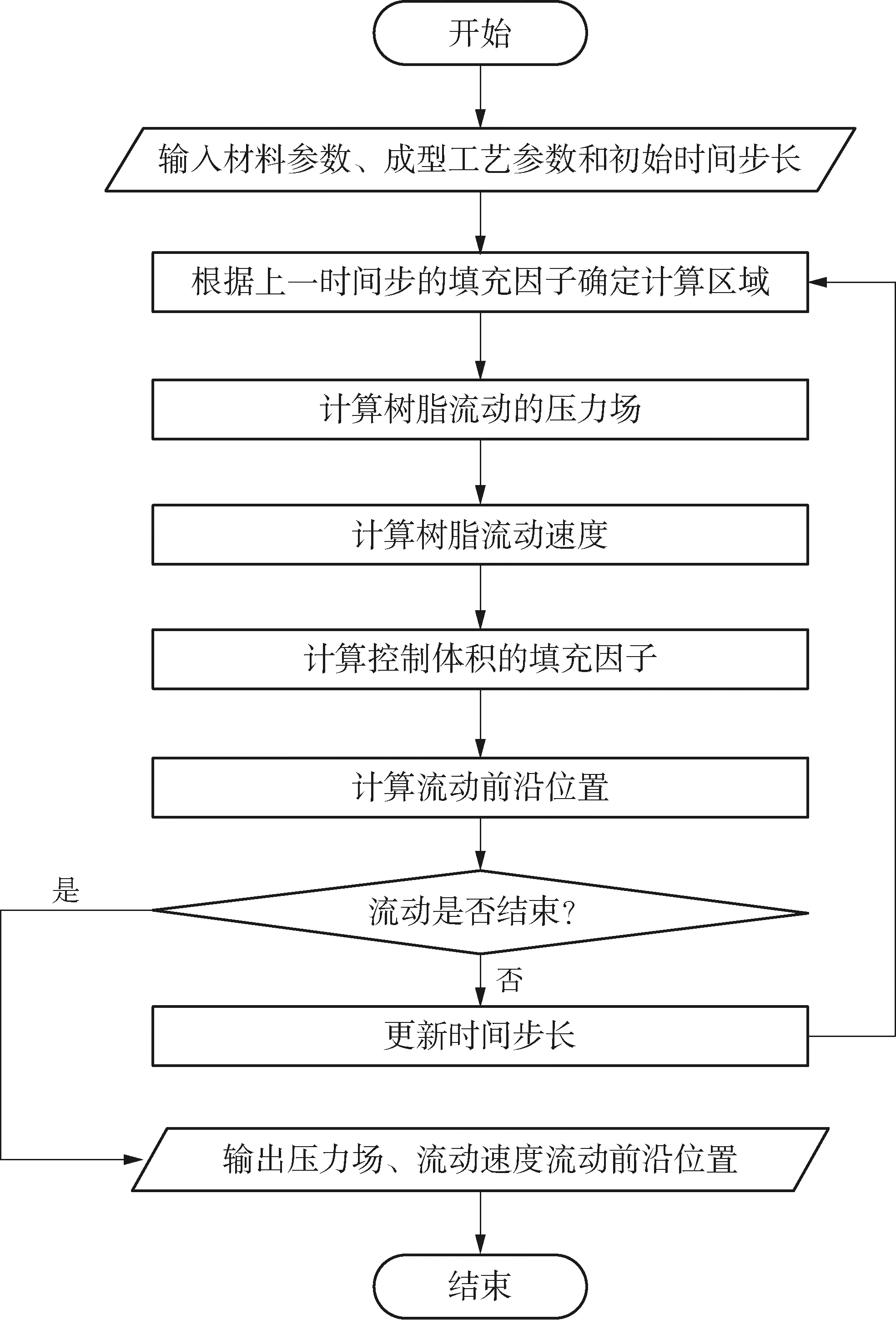
图1 VARTM充填流动计算流程图

2 实验验证

本实验中，单向玻璃纤维布的大小为200 mm×200 mm，浇口位于纤维布的一侧为线型浇口。理论上其他两个方向的渗透率对模拟结果影响较小。实验中采用黏度较小的食用油代替树脂以获得更好的流动性和纤维布的重复利用。入口压力为1个标准大气压，即0.101 MPa，真空度(出口压力)为0.001 MPa，渗透率kx为7.46×10-12m2，孔隙率为29.8%，黏度为0.06 Pa·s。如图2所示，可以看出开始阶段，无边缘效应的模型基本可以预测树脂的流动状况。随着流动的进行，边缘效应越来越明显，即边缘区域的密封薄膜、纤维、底板之间存在间隙，间隙内的流动较纤维布内的流动更快，此时采用普通的不考虑边缘效应的模型不能预测实际成型过程中的树脂充填流动过程。

(a) 实验结果

3 带孔结构的纤维预制体的边缘效应

3.1 几何模型与模拟参数

本算例中，如图3所示，在带有两个通孔的矩形区域中铺放纤维，假设外边、内孔的边缘存在边缘效应，其渗透率远大于内部其他区域的渗透率。通过所开发VARTM数值模拟软件，对不同区域设置不同的渗透率甚至孔隙率，可以方便地研究这些边缘效应区域对树脂流动的影响。模拟参数为：入口压力为0.101 MPa，真空度(出口压力)为0.001 MPa左右，正常区域内的纤维孔隙率为0.25，平面方向的渗透率为1×10-9m2，树脂黏度为0.1 Pa·s，边缘效应区域内的孔隙率为0.35、渗透率为1.0×10-8m2。

图3 边缘效应区域

通过设计不同的浇口来探索VARTM成型该类制件时边缘效应的影响。分别设置树脂短边线注入、短边点注入、中心点注入等5种注胶方式，对较薄制件使用中面模型进行数值仿真分析，长边点注入、长边线注入的情形类似，在此不作讨论。

3.2 模拟结果分析

3.2.1 短边线浇口

当左侧短边线作为浇口时，考虑边缘效应和不考虑边缘效应的数值模拟结果如图4～图6所示。从图4可以看出，边缘效应区域虽然很小，但是显著提高了充填速度，缩短了充填时间。考虑边缘效应时，树脂不仅在边缘区域快速渗透流动，同时也往内部区域渗透，影响内部区域的树脂流动方式，最终会改变干斑出现的位置和可能性。边缘效应导致图5(a)中，由于树脂优先充填右侧边缘区域，充填满后对内部区域形成了包围，导致右侧中心靠内的位置成为最后充填的位置，该局部位置的气体失去了向右侧排气的通道，最终可能在该局部区域出现干斑。虽然图5(b)中右边中心位置是最后充填的位置，但是该位置在右侧边上，而不是右边靠内，该处的气体可以方便地从右侧边的排气通道顺利排出，所以尽管该位置可能出现干斑，但容易排气，实际出现干斑的可能性很小。另外可能出现干斑的位置是两个内孔周围区域，由于内孔区域往往不是排气位置，所以需要注意加强内孔周围的排气。图6(a)中，存在边缘效应时压力分布更加均匀，最后充填位置处的压力变化较快。

(a) 考虑边缘效应

(a) 考虑边缘效应

(a) 考虑边缘效应

3.2.2 短边中心浇口

当左侧短边中心位置作为浇口时，考虑边缘效应和不考虑边缘效应的数值模拟结果如图7～9所示。此时边缘效应的影响同左边线作为浇口时类似，考虑边缘效应时在右侧中心靠内的位置出现干斑。由于左边中心作为浇口时比左侧边线作为浇口时的浇口面积小，所以充填时间呈现较大增长，并且容易在浇口位置形成较大的压力梯度。因此在VARTM工艺中，应尽量避免小截面积的点浇口，而采用具有一定半径(浇口半径)的近似点浇口，减少浇口附近的压力梯度，提高数值模拟的准确性。比较图4与图7，可以发现采用左侧边中心点浇口的充填时间较长，一般在VARTM工艺中宜将点浇口与线浇口结合，即点浇口连接螺旋管，这样树脂经过点浇口之后快速流入螺旋管，进一步渗透到纤维预制体内。

(a) 考虑边缘效应

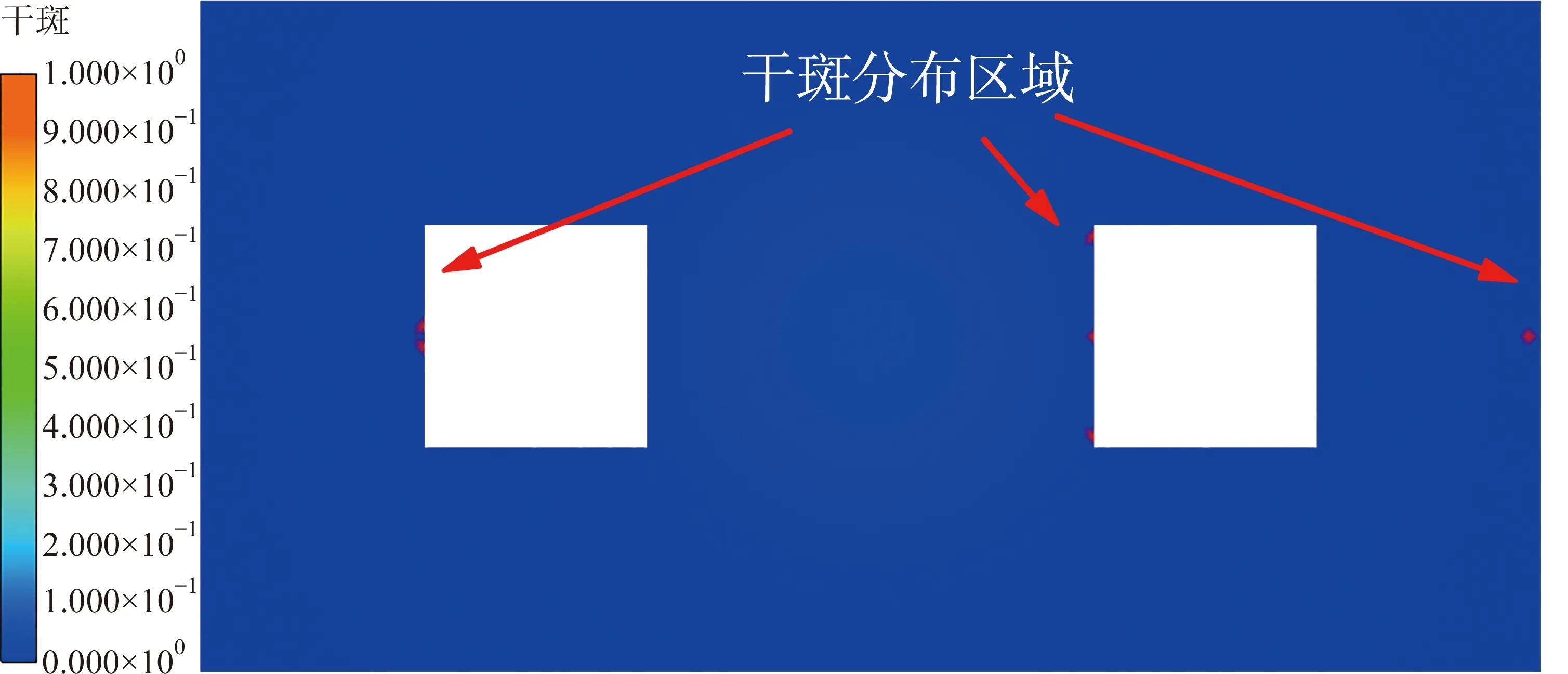
(a) 考虑边缘效应

(a) 考虑边缘效应

3.2.3 内部中心浇口

当内部中心作为浇口时，如图10所示，充填时间较短边线作为浇口时的充填时间还要短得多，这是由于内部中心到周边的充填路径短，在充填压力一定的情况下，充填路径越短，充填速度越快，充填时间越短。此时边缘效应的影响与前面短边线浇口、短边中心浇口类似，最后充填的位置在左右两侧中心靠内的局部位置，该位置的排气通道被周围已充填的树脂阻挡，容易形成干斑，如图11(a)所示的左右两侧边中心靠内的位置。但此时内孔周围干斑消失，而不考虑边缘效应时，内孔周围的干斑仍然可能出现，这是由于两个内孔离浇口近，边缘效应导致内孔周围快速充填。

(a) 考虑边缘效应

(a) 考虑边缘效应

(a) 考虑边缘效应

4 结 论

本文建立了VARTM成型过程中树脂充填纤维预制体的中面计算模型。设计了单向流动实验，验证了模型和数值模拟软件的准确性。模拟并分析了带内孔的纤维预制体充填过程中的边缘效应。边缘效应会导致树脂在边缘位置快速充填流动而封闭内部气体的排出通道，进一步形成干斑缺陷，浇口对干斑位置有重要影响，纤维预制体中心浇口由于具有较短的充填路径，能提高充填速率和缩短充填时间。通过数值模拟研究VARTM成型过程中可能产生干斑的区域，可以为浇口、排气的优化设计提供科学依据。