基于韦伯模式的课程标准与试题一致性分析——以青海师范大学高等数学课程期终试卷为例

贾秀芹,赵青林

(1.青海师范大学 数学与统计学院，青海 西宁 810016;2.青海师范大学 研究生院，青海 西宁 810008)

一致性可以解释为多种事物之间相吻合的程度.课程一致性研究起源于美国20世纪80 年代发起的“由标准驱动并基于标准”的基础教育课程改革，并把课程与教学的一致性做为检测课程标准的一项关键指标[1].

课程一致性评价通常用于基础教育中的教材、课程标准、课程实施、课程达成和课程评价等要素之间的吻合程度.我国在大力推进基础教育课程改革的背景下，引入了西方一致性研究模式，在我国基础教育教学领域进行了课程标准的一致性分析和研究.由于基础教育有统一的课程标准以及统一的高考模式，所以基础教育的课程一致性研究涉及的领域广，普及率高.在高等教育领域，这部分研究相对较少，主要原因是高等院校没有统一的课程标准，同一门课程在不同院校、不同专业领域的教学要求、课程达成度、评价体系均有不同，评价结果不具备普遍性.但是，对于同一所院校的某一门课程而言，教学大纲和考试模式相对稳定，因此通过教学大纲、考试大纲、教学达成度、教学评价等多方面的一致性研究，对于提高这门课程的教学质量有很大的促进作用，所以高校教学大纲一致性评价有其研究意义.

高等数学课程是高等院校开设的一门重要的公共基础课程，是理工科专业的一门必修通识课，该课程的教学内容在不同院校，不同专业领域里存在较高的相似度.基于以上原因，本文运用韦伯一致性分析模式，对我校高等数学课程教学大纲与期终试题进行一致性分析，为提高教学质量提供参考.

1 韦伯模式简介

目前国际上比较成熟的一致性分析模式有“SEC分析模式”“韦伯分析模式(webb)”“成功分析模式(Achieve)”[2].本文选用的是由诺曼·韦伯(Norman L.Webb)创建的韦伯分析模式，韦伯模式使用四个标准来比较评价与课程标准之间的一致性[3].

第一，类别一致性，即评价与课程标准是否陈述了相同的内容范畴.如果包含了相同的或一致内容类别，则认为符合类别一致性标准.可以根据评价试题是否包含了某一条标准的相应内容来判断类别一致性标准的达成与否.评价至少6 次“命中”某一条标准内容，如果有6道试题对于某项次级标准，就可合理地估计学生对其的掌握情况[4].

第二，知识深度一致性，即评价所要求学生展示的认知水平与课程标准中所期望的学生所应知道与能做的认知表述，二者是否保持一致.判断标准是：测验试题的认知水平至少有50%命中课程标准所要求的认知水平.

第三，知识广度一致性，是指课程标准中期望学生所掌握的知识范围与评价试题的知识范围的吻合程度.知识广度一致性将50%作为可接受水平.

第四，知识分布平衡性，是指目标所对应的试题是否分布平衡，或试题是否更重视某一目标及重视程度.平衡指数以≥0.7作为可接受水平[5].

一致性可接受水平判断标准见表1.

2 高等数学课程教学大纲和试题的编码

研究对象：2019—2021年青海师范大学高等数学(上)课程期终试卷.

研究方法：韦伯一致性分析模式.

分析过程：由编码、数据统计、一致性分析三部分构成.

2.1 教学大纲编码说明

选用韦伯一致性分析模式中“金字塔式”的课程目标分析方法[6]，将高等数学课程教学大纲分为三个层级.

第一层，学习领域，指对课程目标的一般描述.高等数学(上)教学大纲中的知识内容分为四个领域，具体为：函数与极限、导数与微分、微分中值定理与导数的应用、不定积分.

第二层，学习主题，是对学习领域的补充，是领域下设的内容.例如，函数与极限领域下分设了三个主题，具体是：函数的概念、数列的极限、函数的极限.

第三层，具体目标，是课程内容的具体目标，每个学习主题下设不同的具体目标.

2.2 教学大纲的编码

对四个领域分别用数字“1、2、3、4”编码，领域下设的主题用“1.1、1.2、1.3…”编码，主题下设的具体目标用“1.1.1、1.1.2、1.1.3…”编码.

根据韦伯分析模式知识深度水平共划分成四个等级，分别是水平1、水平2、水平3、水平4.等级的划分以对应的行为动词作为参考.

水平1：对应的动词有，了解、知道、说出、识别、描述等.

水平2：对应的动词有，理解、比较、使用、认识、能用等.

水平3：对应的动词有，掌握、分析、推导、归纳、探究等.

水平4：对应的动词有，运用、证明、解决、解释、讨论等.

高等数学(上)教学大纲编码(微分中值定理与导数的应用部分)见表2.

表2 高等数学(上)课程教学大纲具体目标编码(部分)

2.3 对高等数学(上)期终试卷的编码

试卷编码：试卷每道题目所涉及的具体目标记为题目数，如果一道题目涉及到两个或多个具体目标，题目数记为2个或者多个.试卷每道试题涉及具体目标数的总和为“测试题目总数”.

此题可考察无穷小等价代换的应用、第一重要极限的应用和洛必达法则的应用，根据与2.2中数学大纲编码库比对，此题命中三个具体目标，编码为1.3.3，1.3.4，3.1.3，题目数为3.

根据教学大纲对知识水平的要求“掌握两个重要极限”“掌握无穷小的等价代换”“掌握洛必达法则的运用”，此题三个考察目标均符合教学大纲知识深度水平中的水平3，所以认知水平确定为水平3.

3 数据统计与分析

本文从知识种类、知识深度、知识广度、知识分布平衡性四个维度进行高等教学课程教学大纲与试题的一致性评价的数据统计与分析.

统计数据的显示以2021年《高等数学》期终试卷为例.

3.1 知识种类一致性

2021年高等数(上)期终试卷知识种类一致性如表3所示：

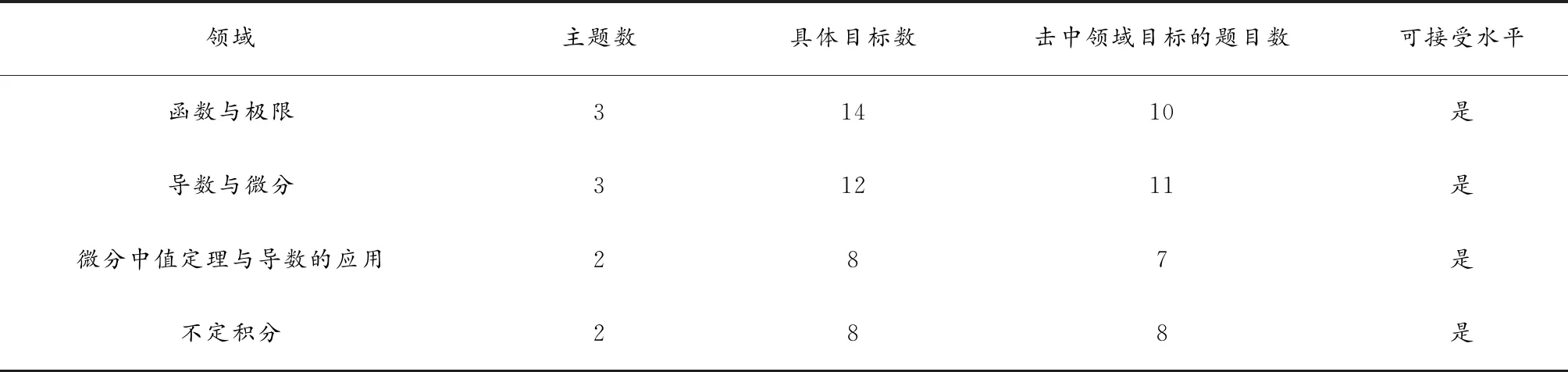
表3 试卷知识种类一致性统计表(2021年)

2019年、2020年、2021年高等数学(上)期终试卷一致性如图1所示.图1显示，2021年我校高等数学课程期末试卷，按照知识种类一致性评价标准，试卷四个知识领域与教学大纲的一致性均为可接受水平.说明试卷中所涉及的知识类型与教学大纲的要求一致性较高.

图1 高等数学课程的期终试卷在知识种类一致性维度上的统计结果

2020年我校高等数学课程期末试卷，知识领域中中值定理与导数的应用和不定积分两部分与教学大纲的一致性为不可接受.试卷中可以适当增加这两个知识领域知识点的测试题目.

随着高等教育流程的不断更新，应用、发挥大数据已经成为促进教育革新、提高教育质量、保证管理效率的必然选择。教育大数据是教育信息化步入新时代的重要标志，教育大数据可以为扶贫决策提供精准、有效、可靠的数据支持，促进教育智力资源的流转与精准供给；对于推进教育管理从经验型、粗放型、封闭型向精细化、智能化、可视化转变也具有重要意义；还有助于构建多维度的科学评价体系，促进规模化中的个性化教育。

2019年我校高等数学课程期末试卷，知识领域中积分部分与教学大纲的一致性为不可接受.试卷可以增加不定积分内容的测试题目.

综合来看，三年的期终试卷，2021年的期终试卷在知识种类一致性这一维度达成度最高.

3.2 知识深度一致性

2021年高等数学(上)期终试卷知识深度一致性情况如表4所示：

表4 知识深度一致性统计表(2021年)

2019年、2020年、2021年高等数学(上)期终试卷关于知识深度的一致性如图2所示.根据图2显示，高等数学课程期终试卷，按照知识深度一致性评价标准，2019-2020年三套试题每个知识领域的知识深度与教学大纲一致性均为可接受水平.说明我校试卷的难易程度和教学大纲一致性程度较高.

图2 高等数学课程的期终试卷在知识深度一致性的统计结果

3.3 知识广度一致性

2021年高等数学(上)期终试卷知识广度一致性如表5所示：

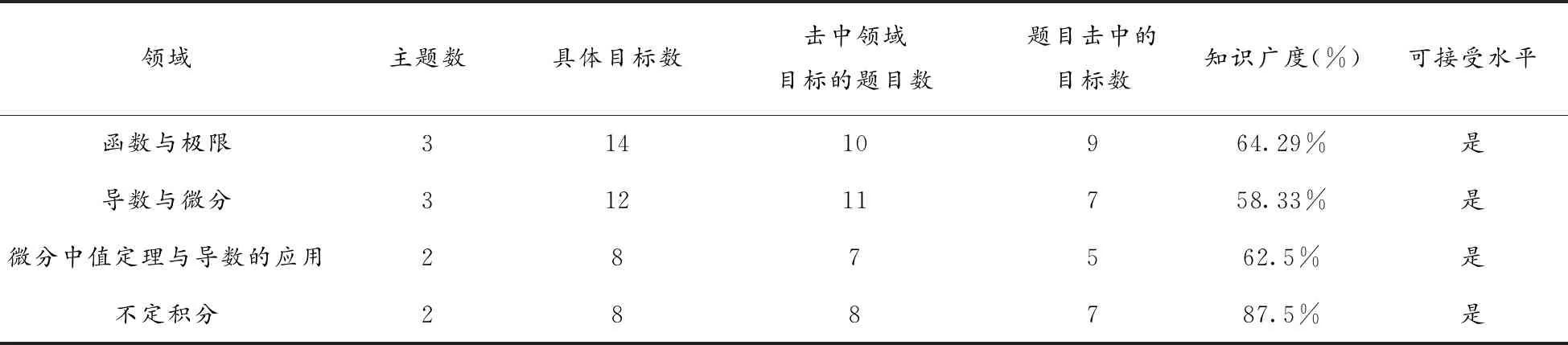
表5 知识广度一致性统计表(2021年)

2019年、2020年、2021年高等数学(上)期终试卷关于知识广度的一致性如图3所示.图3显示，2021年我校高等数学课程期终试卷，按照知识广度一致性评价标准，试卷四个知识领域与教学大刚的一致性均为可接受水平，说明这套试卷的知识覆盖率很好.

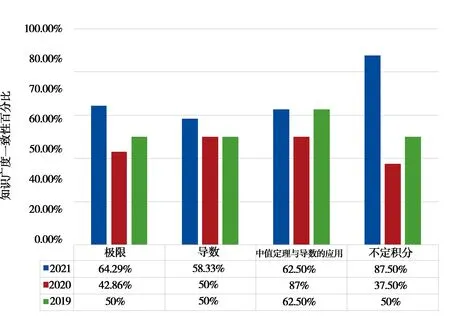
图3 高等数学课程的期终试卷在知识广度的一致性统计结果

2020年高等数学课程期终试卷，极限和不定积分两个知识领域与教学大纲的一致性为不可接受水平，说明这套试卷的知识覆盖率需要进一步调整.

2019年高等数学课程期终试卷，不定积分知识领域与教学大纲的一致性为不可接受水平；极限和中值定理与导数的应用两个知识领域刚刚达标.

综合三套试卷的数据比对得出，2021年《高等数学》试卷的知识广度与教学大纲的一致性达成度最高.

3.4 知识分布平衡性

2021年高等数学(上)期终试卷知识分布平衡指数如表6所示.

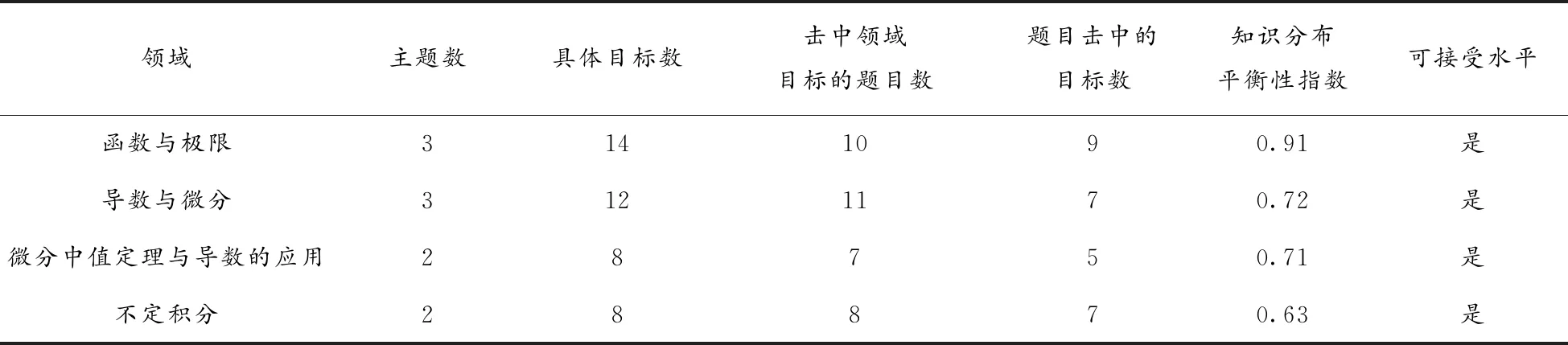
表6 知识分布平衡指数统计表(2021)

2019年、2020年、2021年高等数学(上)期终试卷关于知识分布平衡指数如图4所示.图4显示，我校高等数学课程期终试卷，按照知识分布平衡性的评价标准，2019年和2020年两套试题的知识分布平衡性与教学大纲的一致性均为可接受水平.

图4 高等数学课程的期终试卷在知识分布平衡性一致性的统计结果

2021年试卷中不定积分的分布平衡指数小于0.7，知识分布平衡性与教学大纲的一致性为不可接受.

4 结论

运用韦伯一致性分析模式，对我校2019—2021年三年的高等数学(上)期终试卷与教学大纲的一致性进行分析，分析结果汇总见表7.

表7 2019—2021年高等数学课程期终试卷一致性判断汇总表

根据表7分析结果如下：

试卷极限部分：三套试卷与教学大纲的一致性较高，其中2020年的试卷需要在知识广度的维度加以调整.

试卷导数部分：三套试卷与教学大纲完全达到一致性可接受水平，试卷与教学大纲的一致性最好.

试卷中值定理与导数的应用部分：三套试卷与教学大纲的一致性较高，其中2020年试卷中知识类别未达到一致性可接受水平，可以做出适当调整.

试卷不定积分部分：三套试卷与教学大纲的一致性相对较低，其中2021年试卷中知识分布平衡性，2020年试卷中知识类别和知识广度，2019年试卷的知识广度，共计四次未达到一致性可接受水平，说明在命题时对这个知识领域的考察需要调整.

总之，高等数学课程的命题以学校制定的教学大纲为主，命题教师不同，对试卷编码的认定标准会有偏差，这会影响试卷最终一致性判断的结果.如何降低由此带来的误差，使得教学要求、课程达成度、评价体系有较高的一致性，还需要教师从多方面、多层次、多角度探讨教学目标和专业需求等因素.最终，通过整合评价标准，优化评价体系，合理拟定试卷，更好地促进我校高等数学课程的教学工作.